|
|
| |
CAPITOLO 1
INTRODUZIONE
Durante il corso verranno trattati soprattutto segnali elettrici che sono quei segnali presenti su un filo tra 2 connettori, dove andiamo a manipolare correnti, tensioni e potenze (le tre grandezze fondamentali per l'elettronica); i segnali elettrici possono essere generati da diversi tipi di sorgente, per esempio da trasduttori (microfono, termocoppia, ...):
![]()
![]()


![]()
Se Se' Su Segnale
di Entrata 343i88d (non
elettrico) Fig 1.1
La più semplice e banale elaborazione di un segnale elettrico è l'AMPLIFICATORE (che vedremo in dettaglio durante il corso).
I segnali possono essere esaminati secondo 2 punti di vista: il punto di vista analogico e il punto di vista digitale. Dello stesso segnale (che è una grandezza comunque e sempre continua) possono interessarci solo certi valori ben definiti, oppure tutti i valori che esso assume nel tempo.
Questo segnale
può essere considerato un segnale analogico in quanto può assumere
infiniti valori (cioé TUTTI i valori tra il suo massimo e il suo
minimo). Se invece prendo in
considerazione soltanto alcuni valori o alcune fasce di valori (ad es. i
valori compresi nelle 2 fasce tratteggiate) questo segnale può essere considerato
un segnale discreto, perché assume solo 2 valori per me
significativi. Quindi ogni fenomeno può essere trattato sia dal punto di
vista analogico che dal punto di vista digitale; per esempio possiamo dire
che in aula la luce è accesa oppure è spenta (analisi digitale) ma possiamo
anche dire che in aula è presente una determinata quantità di luce e di
ombra (analisi analogica).
Prendiamo in considerazione il seguente segnale:

Per passare da una descrizione analogica di un segnale ad una digitale è necessario avere infiniti segnali digitali; questa affermazione ci porta a pensare che il passaggio da analogico a digitale sia impossibile. In realtà tutte le grandezze fisiche sono note a meno di un errore e; di conseguenza non serviranno più infiniti segnali digitali per descrivere un segnale analogico, ma sarà sufficiente un numero di segnali tale per cui l'errore di discretizzazione che si commette è minore dell'errore di approssimazione:
|
|
N = numero di segnali digitali ed = errore di discretizzazione e = errore di misurazione |
Per esempio, se voglio un errore non superiore all' 1%, mi bastano 7 segnali digitali per rappresentare il segnale analogico:
N=7 ed = 1 / 128 < e
Se invece voglo un errore non superiore all'un per mille, mi bastano 10 segnali digitali:
N=10 ed = 1 / 1024 < e
Nella pratica si utilizzano 12 oppure 16 bit che sono più che sufficienti per discretizzare qualunque segnale analogico.
I circuiti che manipolanosegnali elettrici devono mantenere la qualità del segnale in uscita pari a quella del segnale in ingresso. Se all'ingresso ho un errore dell' 1%, all'uscita devo ancora avere la stessa precisione. Per i segnali analogici, la fedeltà dipende dalla qualità del circuito; nel caso di segnali digitali non c'è più questo problema, perché i valori che il segnale può assumere sono noti e definiti, quindi possono essere facilmente riprodotti in uscita. D'altro canto occorrono più circuiti digitali per fare lo stesso lavoro di un solo circuito analogico. Inoltre, un circuito analogico è, in teoria, istantaneo, mentre per il circuito digitale occorre del tempo per fare le 2 conversioni di segnale (analogico digitale, digitale analogico), e in pratica fenomeni con frequenza più grande del kiloHz sono difficilmente trattabili in digitale.
Riassumendo:
|
DIGITALE |
ANALOGICO |
|
+ Semplice da realizzare |
- Semplice |
|
- Costoso |
+ Costoso |
|
+ integrazione più facile |
- Integrazione meno facile |
|
- Veloce |
+ Veloce |
Scopo: l'amplificatore è quel circuito che modifica l'ampiezza del segnale secondo una certa legge o caratteristica.
Sono dei circuiti nei quali entra un segnale Se in ingresso e dai quali esce un segnale Su, con la stessa forma di Se (fedele) ma amplificato.
Un amplificatore non fedele produce un segnale distorto.
Se ci troviamo
di fronte un amplificatore lineare, la legge che lega il segnale di
uscita Su con quello di entrata Se sarà la seguente: Su = K * Se con K costante
Fig
1.3

Ad esempio, se in ingresso abbiamo una sinusoide:
Se = A * sen wt Su = KA * sen wt
Se su un grafico poniamo in ascissa l'ampiezza di Se e in ordinata l'ampiezza di Su, siccome K è costante otteniamo una retta, teoricamente di lunghezza infinita, il cui coefficiente angolare è appunto K (fig 1.4).

In realtà la retta non è infinita, perché il circuito è limitato sia verso il basso che verso l'alto (fig 1.5).
Come indicato
in figura, l'intervallo tra le due linee tratteggiate orizzontali è
chiamato dinamica del segnale d'uscita, l'intervallo tra le due
linee tratteggiate verticali è chiamato dinamica del segnale d'ingresso.

Questo significa che un amplificatore reale ha una zona di linearità limitata e definita, all'interno della quale il segnale è amplificato secondo la legge lineare con coefficiente K.
Ovviamente non tutti gli amplificatori hanno una caratteristica lineare. Esistono amplificatori con caratteristica quadrata, logaritmica (ad es. per compattare un segnale), non lineare (utili per linearizzare un sistema in cui un componente, per es. un sensore, non è lineare).
Finora abbiamo sottinteso che il valore di K fosse indipendente sia dalla pulsazione w che dall'ampiezza A, ma questo non è vero nella realtà. Possiamo ottenere che il valore di K sia indipendente da w per un campo ristretto di frequenze (quindi ci troviamo di fronte ad un amplificatore selettivo o Tuned) oppure per un campio molto ampio di frequenze (e quindi abbiamo gli amplificatori non selettivi o Untuned ).
Il valore di K, che dipende dalla frequenza, lo si può esprimere come una funzione: K(w ; questa è detta funzione di trasferimento, e ne studieremo la forma e le caratteristiche. Inoltre, il legame tra K e w viene studiato mediante la curva di risposta in frequenza, che esprime appunto il comportamento di K al variare di w
Visto che gli amplificatori hanno in ingresso un segnale a cui è associata una determinata potenza e che in uscita hanno un segnale a cui è associata una potenza maggiore di quella del segnale di ingresso, deve esistere nel circuito una sorgente di potenza (non posso entrare con 1 W e uscire con 10W!)(fig 1.6).
La sorgente di potenza è di solito un alimentatore (componente di cui
studieremo le caratteristiche). Le
tensioni di alimentazione sono quelle che introducono quelle limitazioni inferiore
e superiore nella dinamica dei segnali amplificati
(vedi Fig.1.5). Inoltre l'alimentatore ha il compito di polarizzare (to bias) i dispositivi che
costituiscono l'amplificatore in modo da farli funzionare correttamente
(cioé in linearità). Fig 1.6

Scopo: possiedono una determinata e precisa risposta in frequenza.
Si suddividono in:
filtri passivi: sono circuiti realizzati solo con elementi passivi (resistori, condensatori, trasformatori, induttori, ....), quindi non hanno bisogno dell'alimentazione.
filtri attivi: hanno al loro interno anche elementi attivi (amplificatori) e questo implica la presenza dell'alimentazione.
Con i componenti attivi posso ottenere le stesse leggi di funzionamento dei componenti passivi, ma con il vantaggio di non utilizzare induttanze e trasformatori, che sono difficili da realizzare e molto imprecisi.
Nei filtri si vuole realizzare un ben preciso legame tra funzione di trasferimento e frequenza, cioé si vuole un determinato valore di amplificazione a una determinata frequenza; ciò implica un comportamento in frequenza del filtro estremamente preciso; mentre negli amplificatori ciò non è necessario, infatti è sufficiente che la frequenza non dia fastidio.
Tra tutti i possibili circuiti non lineari, consideriamo quelli che presentano 2 stati di funzionamento (fig 1.7).

Esempio tipico è il comparatore di soglia, che vedremo nei dettagli più avanti.
I circuiti con una caratteristica non lineare come quella vista ora, sono i mattoni base per la realizzazione dei generatori di segnale o di forme d'onda. I generatori più diffusi sono quelli che creano onde quadre, sinusoidali, triangolari, a dente di sega.
Scopo: Trasformano una sorgente di energia primaria in una fonte di energia adatta ad alimentare i vari circuiti elettronici.
Caratteristiche:
hanno un buon rendimento (consumano poca potenza rispetto a quella prelevata dalla sorgente).
mantengono sufficientemente costante il segnale in uscita, indipendentemente da:
a - le variazioni del carico
b - le variazioni della sorgente primaria
c - le variazioni della temperatura
Quelli che si comportano così sono chiamati alimentatori stabilizzati.
I circuiti digitali sono quei circuiti che trattano e manipolano segnali digitali. Si possono suddividere in base alla tecnologia con cui sono stati costruiti in:
- BIPOLARI (più adatto a circuiti analogici)
- MOS
- CMOS
- BCMOS
e in base alla funzione che svolgono in:
- combinatori (l'uscita segue l'ingresso istante per istante)
- sequenziali (le variazioni dell'ingresso e dell'uscita sono scandite con una certa frequenza)
I circuiti più diffusi sono:
- Microprocessori
- Microcontrollori
- Memorie
Sono sistemi in cui coesistono circuiti analogici e circuiti digitali. Tali circuiti sono separati in tutto tranne nell'alimentazione.
I sistemi più diffusi sono:
- Sistemi di conversione Analogica digitale (ADC)
- Sensori
- Synchro, LVDT, RVDT
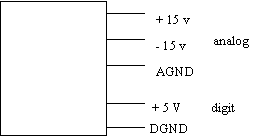
I circuiti analogici richiedono un'alimentazione diversa da quella digitale (fig 1.8).
Problemi: i circuiti analogi, dovendo essere precisi, devono avere
alimentazioni stabili (variazioni di 1 mV) l'assorbimento di potenza nei
circuiti analogici è più o meno costante, mentre in quelli digitali,
specialmente nei sequenziali, avviene in modo impulsivo (in quanto
richiedono corrente in modo impulsivo) Fig 1.8
Infatti:
V = L (di/dt) dove di è dell'ordine degli Ampere
dt è dell'ordine dei nanosecondi
quindi V subisce variazioni dell'ordine dei Volt
Sulle piste dei circuiti digitali esistono disturbi molto elevati: una pista può essere vista come una piccola induttanza.
Per risolvere questi problemi il primo accorgimento consiste nello separare i percorsi di massa. In altre parole dobbiamo evitare la situazione descritta in fig 1.9.
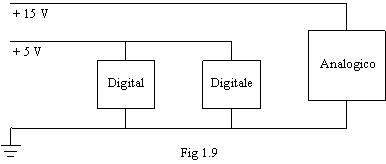
Nello schema di fig 1.9 la corrente del 5 V si accoppia con quella del 15 V verso massa.
NOTA: il riferimento di massa deve essere lo stesso per i due circuiti, altrimenti non possono assolutamente comunicare.
Quidni la situazione corretta è la seguente, dove le masse convertono in un solo punto:
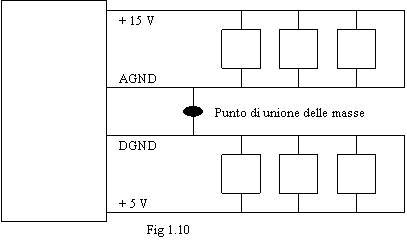
Se i punti di contatto fossero 2 otterrei una maglia (anello di massa), e questa situazione provoca disturbi e occorre evitarla (anche se in certi casi non è possibile agire altrimenti).
I componenti sia attivi che passivi possono essere in 2 forme:
- discreta: ogni componente del circuito è un singolo componente elettronico: una resistenza, un condensatore, un induttore, ecc. collegati tra loro tramite fili e piste; la progettazione di circuiti discreti è ancora utlizzata in due settori: la potenza e l'iperfrequenza.
Per dare un'idea, siamo in zona di potenza quando lavoriamo con correnti di decine e centinaia di Ampere. Ci troviamo in questa situazione soprattutto nelle zone di interfaccia verso gli attuatori. Nelle applicazioni per iperfrequenze la lunghezza d'onda del segnale è comparabile alle dimensioni dei componenti elettronici (il modello a parametri concentrati non vale più e occorre utilizzare il modello a parametri distribuiti).
- integrata: su un unico supporto di silicio (ad alte frequenze si utilizza l'Arseniuro di Gallio: GaAs) sono integrati moltissimi componenti. Sono presenti solo resistori e piccoli condensatori, più facili da realizzare e da integrare. Ovviamente se devo inserire induttanze o trasformatori torno ai circuiti discreti.
Sugli integrati è possibile impaccare tantissimi transistor, ma esistono difficoltà ad inserire resistenze con valori molto diversi tra loro, in quanto la tecnologia usata per fare una resistenza di 1KW è diversa da quella usata per una resistenza di 1MW, perciò occorre inserire resistenze tutte dello stesso ordine di grandezza.
Inoltre ci sono grossi problemi nella realizzazione di resistenze di valore preciso e predeterminato; quindi è meglio lavorare sui rapporti tra resistenze perchè è molto semplice, lavorando sui parametri geometri della resistenze, fare una resistenza di valore multiplo di un'altra:
![]()
dove r è la resistività del materiale, l è la lunghezza e A è l'area. Lavorando su l e A (parametri geometrici) ottengo resistenza tra loro proporzionali con elevatissima precisione.
Per fare il nostro progetto possiamo utilizzare:
- circuiti standard: componenti come contatori, amplificatori, ...., che portano ad un basso costo di realizzazione ma comportano un elevato numero di collegamenti, saldature, componenti da collegare.
- circuiti integrati dedicati: sono poco flessibili (full custom).
- circuiti semidedicati: sono circuiti abbastanza generici programmabili dall'utente (PAL, macrocelle, ALTERA, XILINX).
Cosideriamo il circuito di fig 1.11.
|
Fig 1.11 | Se sono in corrente continua, la potenza che entra nel circuito sarà: P = V I. Per effetto Joule questa potenza viene convertita in calore, quindi la temperatura del dispositivo cresce, e le variazioni di temperatura provocano gravi disturbi a qualunque tipo di circuito. Il problema è particolarmente sentito nei semiconduttori (silicio); gli effetti della temperatura possono essere di 2 tipi: cambiamento delle caratteristiche di funzionamento del dispositivo (derive termiche o drift) effetto distruttivo: se la temperatura supera certi valori il dispositivo si danneggia in modo irreparabile |
|||||||||||||
La temperatura limite di funzionamento Tj (temperatura di giunzione) varia a seconda del materiale:
- Silicio: 200°C per circuiti semplici
175°C per circuiti più complessi
150°C per CPU, memorie, ...
- Arseniuro di Gallio: 150°C per tutti i componenti
- Germanio: 125°C per tutti i componenti (non si usa più)
Se la temperatura del componente supera il valore Tj , il componente si danneggia irreparabilmente.
Esistono alcuni range di temperatura standard, cioè intervalli di temperatura ambientali in cui i dispositivi rispettano le specifiche; i principali sono:
RANGE COMMERCIALE 0°C - 70°C
RANGE MILITARE -55°C - 125°C
range industriale: a metà tra i due precedenti (ad es. -20°C - +100°C)
I primi due sono standard, l'ultimo no.
|
| Analizziamo ora nei particolari la temperatura che circonda i vari componenti; prendiamo in considerazione un componente generico raffigurato qui a sinistra. Per capire il legame tra la potenza dissipata e la differenza di temperatura mettiamoci in condizioni ideali (fig 1.12). |
Giunzione J Ambiente A Tj TA Parete di separazione omogenea Fig 1.12
![]()
![]()
![]()
Sorgente di Potenza P
La sorgente di potenza P modella il circuito che si trova dentro il case. La parete omogenea modella la parete del case che separa i due ambienti.
Ipotizziamo che la
distanza tra P, considerata puntiforme, e la parete sia tale che dal punto di
vista della sorgente P la parete sembri infinita; sotto questa ipotesi il
legame tra la temperatura di giunzione ![]() e la temperatura ambiente
e la temperatura ambiente ![]() è lineare:
è lineare:
![]()
dove ![]() è la resistenza
termica (in alcuni casi si ha la conduttanza termica
è la resistenza
termica (in alcuni casi si ha la conduttanza termica ![]() ).
).
La resistenza
termica ![]() dipende dalla forma
del case e dal metariale di cui è
costituito; la potenza dissipata dipende dal circuito posto all'interno del case; in generale, più è piccola
dipende dalla forma
del case e dal metariale di cui è
costituito; la potenza dissipata dipende dal circuito posto all'interno del case; in generale, più è piccola ![]() e migliore è la
dissipazione.
e migliore è la
dissipazione.
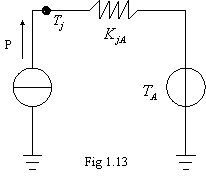
Vediamone l'equivalente elettrico (fig.1.13).
Modello elettrico: Potenza Corrente Temperatura Tensione Resistenza termica Resistenza elettrica Nota: la temperatura TA è
rappresentata da un generatore di tensione perché è una variabile
indipendente, cioè siamo noi (o le condizioni esterne) a stabilirne il
valore; la temperatura TJ invece ci è data dalle specifiche e
non è modificabile.
Alcune considerazioni:
![]() è un dato fisso fornito dal costruttore (ad es. 150°C)
è un dato fisso fornito dal costruttore (ad es. 150°C)
![]() può essere un vincolo
(la temperatura ambiente mi è imposta) oppure una variabile (in base alle altre
variabili calcolo la temperatura ambiente massima)
può essere un vincolo
(la temperatura ambiente mi è imposta) oppure una variabile (in base alle altre
variabili calcolo la temperatura ambiente massima)
P dipende dal circuito:frequenza, dimensioni, ecc...
![]() è la resistenza
termica in aria libera (free air);
il suo valore cambia in presenza di dissipatori (ventole, refrigeranti...). Il
valore KJA calcolato da noi tramite la formula deve risultare uguale
o superiore al valore KJA fornito dal costruttore, altrimenti
occorre un dissipatore.
è la resistenza
termica in aria libera (free air);
il suo valore cambia in presenza di dissipatori (ventole, refrigeranti...). Il
valore KJA calcolato da noi tramite la formula deve risultare uguale
o superiore al valore KJA fornito dal costruttore, altrimenti
occorre un dissipatore.
Siccome i valori TJ e P sono fissi, forniti dal costruttore, noi possiamo fare solo due cose:
Utilizzare il valore ![]() del dispositivo per
calcolare la massima temperatura ambientale TA alla quale il
dispositivo stesso è in grado di funzionare (questa deve risultare comunque
maggiore di 25 °C)
del dispositivo per
calcolare la massima temperatura ambientale TA alla quale il
dispositivo stesso è in grado di funzionare (questa deve risultare comunque
maggiore di 25 °C)
Utilizzare la temperatura
ambientale alla quale il dispositivo dovrà lavorare per calcolare il valore di ![]() che dovrebbe avere. In
questo secondo caso, se ottengo un valore di
che dovrebbe avere. In
questo secondo caso, se ottengo un valore di ![]() inferiore al valore
di
inferiore al valore
di ![]() del dispositivo,
allora è necessario introdurre un dissipatore, perché in aria libera il
dispositivo non è in grado di funzionare.
del dispositivo,
allora è necessario introdurre un dissipatore, perché in aria libera il
dispositivo non è in grado di funzionare.
Per modellare la presenza del dissipatore, si
divide il valore di ![]() in due componenti:
in due componenti: ![]() e
e ![]() (fig 1.14).
(fig 1.14).
|
|
quindi dove KCA rappresenta il dissipatore; scegliendo opportuni valori di KCA possiamo modificare il valore di KJA. |
I fornitori ci
danno indicazioni su ![]() e su
e su ![]() in questa forma:
in questa forma:
|
La potenza
dissipabile @ 25°C di La potenza
dissipabile @ 25°C di temperatura del case con |
Se calcolo un
valore di ![]() maggiore del
maggiore del ![]() fornito allora non
occorre un dissipatore.
fornito allora non
occorre un dissipatore.
Se calcolo un
valore di ![]() maggiore del
maggiore del ![]() fornito e minore del
fornito e minore del ![]() fornito allora occorre
un dissipatore.
fornito allora occorre
un dissipatore.
Se calcolo un
valore di ![]() minore del
minore del ![]() fornito non c'è modo
di far funzionare il dispositivo, con nessun dissipatore; devo cambiare i
parametri di progetto:
fornito non c'è modo
di far funzionare il dispositivo, con nessun dissipatore; devo cambiare i
parametri di progetto:
- cambio ![]()
- cambio la potenza (al posto di andare a 50 Mhz vado a 25 Mhz)
- cambio il Case
Vediamo ora un esercizio utile per la comprensione ed il calcolo della resistenza termica.
Prendiamo in considerazioni 2 contenitori tipici per dispositivi di potenza:
|
|
|
|
|
TO3 |
45°C/W |
5,5°C/W |
|
TO220 |
65°C/W |
5°C/W |
|
[Altri esempi: |
|
|
|
DIL (plastico) |
100°C/W |
30°C/W40°C/W |
|
DIL (ceramico) |
50°C/W |
5°C/ W - 10°C/W] |
Supponiamo di avere ![]() = 150°C e che
= 150°C e che ![]() (potenza dissipata)
sia 2 Watt.
(potenza dissipata)
sia 2 Watt.
- A che temperatura posso andare in aria libera?
Dobbiamo cercare ![]() senza la presenza di
dissipatori.
senza la presenza di
dissipatori.
TO3: 150°C
- ![]() = 45°C/W * 2 W
= 45°C/W * 2 W ![]() = 60°C
= 60°C
TO220: 150°C
- ![]() = 65°C/W * 2 W
= 65°C/W * 2 W ![]() = 20°C
= 20°C
Nel primo caso il dispositivo funziona bene in aria libera perché
normalmente la temperatura ambiente non arriva a 60 °C. Nel secondo caso,
invece, la ![]() ottenuta è più bassa
della temperatura ambiente fissata per convenzione a 25 °C, quindi il TO220 non
va bene per l'applicazione in aria libera, ma necessita di un dissipatore.
ottenuta è più bassa
della temperatura ambiente fissata per convenzione a 25 °C, quindi il TO220 non
va bene per l'applicazione in aria libera, ma necessita di un dissipatore.
-
Se la specifica mi impone ![]() = 90°C, calcolare il
valore della resistenza termica che deve avere il dissipatore.
= 90°C, calcolare il
valore della resistenza termica che deve avere il dissipatore.
Dalle specifiche ambientali (90°C) e da quelle circuitale (2 W di potenza) otteniamo:
150°C - 90°C = ![]() * 2
* 2 ![]() = 30°C/W
= 30°C/W
[Siccome il ![]() ottenuto è minore del
ottenuto è minore del ![]() di entrambi i case,
occorre per entrambi un dissipatore]
di entrambi i case,
occorre per entrambi un dissipatore]
A questo punto
ricordando che ![]() =
= ![]() +
+ ![]() abbiamo:
abbiamo:
TO3: 30°C/W
= 5°C/W +![]()
![]() = 25°C/W
= 25°C/W
TO220: 30°C/W
= 5,5°C/W +![]()
![]() = 24,5°C/W
= 24,5°C/W
Kd non può superare il valore 25°C/W nel primo caso e il valore 24,5°C/W nel secondo caso, ma può avere un valore inferiore, e ciò significa utilizzare un dissipatore più potente.
Per concludere, ricordiamo che la valutazione di quanta potenza utilizza una scheda o un componente è di fondamentale importanza. Infatti:
esistono problemi di temperatura: la potenza in qualche modo DEVE essere dissipata
l'alimentatore deve essere in grado di fornire la potenza necessaria (ho così dei vincoli sulle "dimensioni" del Power Supply)
CAPITOLO 1
SOMMARIO
1.1. Definizioni di segnale analogico e segnale discreto (o digitale).......... ..... ...... .......... ..... ...... .......... ..... ...... ........
1.1.1. Conversione analogico - digitale.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... ......................
1.2. Panoramica sui circuiti analogici più diffusi.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... ...........
1.2.1. Amplificatori.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .........................
1.2.2. Filtri
1.2.3. Circuiti non lineari
1.2.4. Generatori di forme d'onda.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .
1.2.5. Alimentatori (Power Supply)
1.3. Panoramica sui circuiti digitali.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... ...
1.3.1. Sistemi misti (analogici - digitali).......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... ......................
1.4. Problematiche di progetto.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... ..........
1.5. Considerazioni termiche.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .............
1.5.1 Esempio.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... ...
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026