L'analisi della risposta in frequenza si fonda sulla relazione tra la trasformata di Laplace della sollecitazione e quella della risposta.

Diagrammi di Bode

Il diagramma di Bode è un diagramma cartesiano con il quale è possibile rappresentare in funzione della pulsazione w il modulo e la fase di una funzione G(jw). Il modulo e la fase, aventi rispettivamente come unità di misura il decibel e il grado, sono riportati sull'asse delle ordinate in scala lineare, mentre la pulsazione w è riportata sull'asse delle ascisse in scala logaritmica con il logaritmo in base 10. in tal modo il modulo e la fase della funzione di trasferimento armonica G(jw) possono avere una rappresentazione particolarmente efficace con il vantaggio che le operazione di moltiplicazione e di divisione si trasformano rispettivamente in addizioni e sottrazioni.

procedimento

G=20/s*(1+0.5s)*(1+0.01) ; G=20/s+0.501s²+0.005s³

comandi utilizzati

n1=20;

d1=[0.005 0.501 1 0];

bode(n1,d1);

figura:

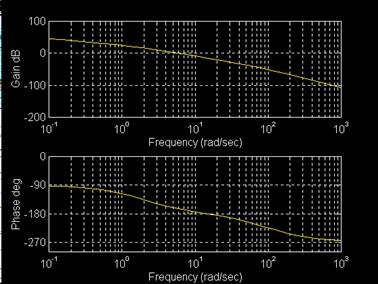
Procedimento 2 con il comando logspace

Per l'esecuzione  di questa prova utilizziamo il programma MATLAB con il quale, utilizzando la funzione di trasferimento

G(s)= 10 (1+s)

1+2s

che equivale a:

G(jw)= 10 (1+jw

1+2jw

ed inserendo le seguenti  stringhe di comando

num= [10 10]

den= [2 1]

W= LOGSPACE (-2, 2, 50)

Bode (num, den, W)

si ottengono i diagrammi del modulo e della fase.

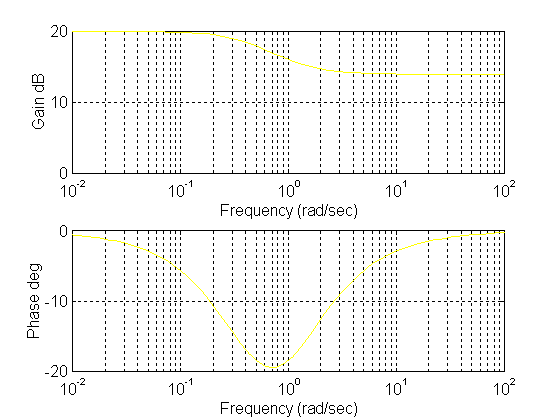
Coclusioni

Mat lab fonisce solo la rappresentazione grafica quando il comando è scritto nella forma Bode(num,dem).

la funzione logspace è definita per definire l'intervallo di frequenza.

Cozzi Marco   cl:5ain Udine 2001

Stabilità

un sistema è stabile se sollecitato con un segnale di ingresso limitato nel tempo l'uscita torna a zero in un tempo finito

Un sistema si dice che è assintoticamente stabile se l'uscita tende a un valore costante (non torna a zero).

Criteri di stabilità

per comprendere meglio il concetto di stabilità lo applichiamo ad una funzione e con matlab lo proviamo

G(jw 1 .

s³+s²+s+0.5

possiamo applicare il criterio di Nyquist perché il numero di poli è maggiore al numero di zeri.

Il criterio infatti dice che un sistema è instabile se la curva mi abbraccia il punto (1,0).

Possiamo calcolare anche il margine di guadagno nel diagramma di Bode con il comando:

margin (n1, d1)

Comandi con MATLAB

num= [0.5]

den= [1 2 1 0.5]

[mag, phase, w]=bode (num, den)

[Gm, Pm, Wcg, Wcp]=margin(mag, phase, w)

nyquist (num, den)

pause

title(['Margine di guadagno=',num2str(Gm),'Margine di fase=',num2str(Pm),'°'])

%Margine di fase e margine di guadagno.

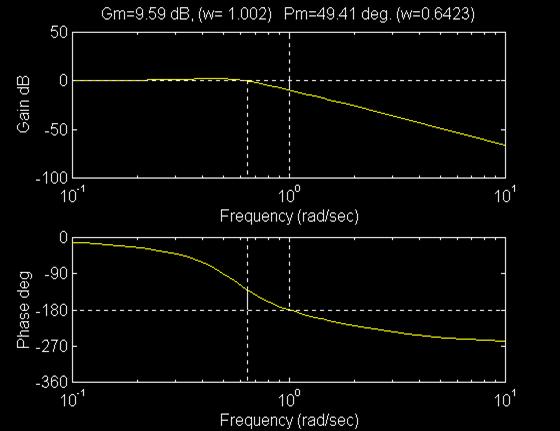
margin(mag, phase, w)

Cozzi Marco CL5AIN    pagina 02

Diagramma di Nyquist

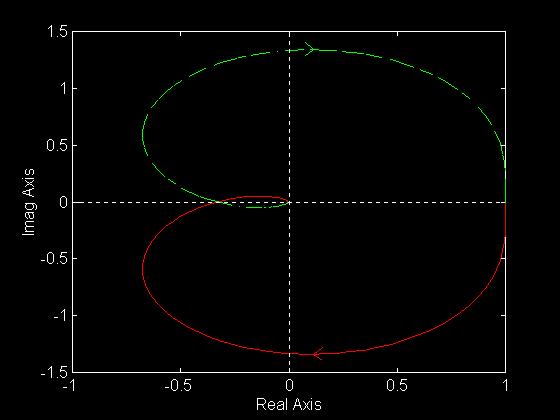
Diagramma di Bode con i margini di guadagno

Cozzi Marco

Classe 5AIN

Diagrammi di Bode