Relazione di informatica per la risoluzione di un'equazione con il metodo della BISEZIONE

informatica

Relazione [FV1] di informatica per la risoluzione di un'equazione con il metodo della BISEZIONE

Obbiettivo del programma

L'obbiettivo di questo programma è determinare le soluzioni delle equazioni nella 939h74j forma    f(x)=0 attraverso il metodo della bisezione.

Considerazioni teoriche

Il metodo della bisezione ci permette di trovare delle approssimazioni delle soluzioni delle equazioni di forma f(x)=0.

Per lavorare con questo metodo occorre conoscere un'approssimazione per difetto a@ ,, e per eccesso b@, della soluzione che cerchiamo c, tali che f(a@) e f(b@) abbiano segni opposti. Fatto ciò bisogna determinare una successione di approssimazioni per difetto e una successione di approssimazioni per eccesso partendo dalla approssimazione a@= a e b@= b determinando le approssimazioni successive con questo metodo:

per calcolare an+1 e bn+1 conoscendo già an e bn:

Si pone

m= an + bn

2

Se f(m) ha lo stesso segno di f(an), allora

an+1=m bn+1= bn

altrimenti

an+1= an bn+1=m

Se f(m)=0 allora m è la soluzione.

Quindi a ogni passaggio le approssimazioni si avvicinano sempre di più al risultato c ma l'eventualità f(m)=0 potrebbe non verificarsi e quindi per arrestare l'algoritmo bisogna inserire una condizione alternativa:

bn -an

essendo є un numero positivo prefissato che rappresenta l'errore massimo accettabile.

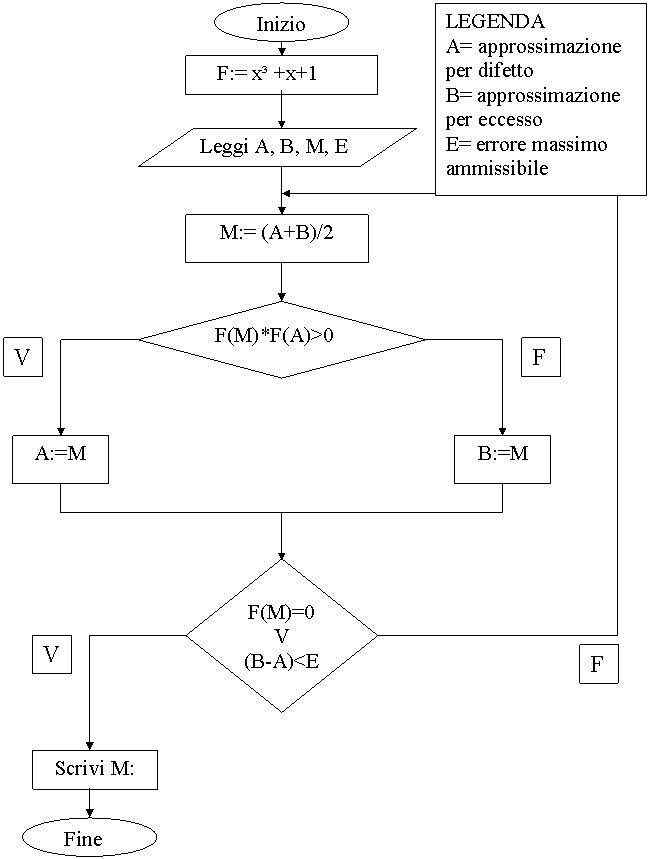
Questo algoritmo può essere riassunto in un diagramma di flusso e tradotto in linguaggio Pascal, usando come esempio l'equazione

x³ +x+1

TRADUZIONE IN LINGUAGGIO PASCAL DEL PROGRAMMA BISEZIONE

Program bisezione;

var A,B,M,E: real;

Function F(X:real):real;

begin

F:=X*X*X+X+1;

end;

begin

write ('scrivere approssimazione per difetto: A=');

readln (A);

write ('scrivere approssimazione per eccesso: B=');

readln (B);

write ('scrivere errore massimo ammissibile: E=');

readln (E);

repeat

M:=(A+B)/2;

if F(M)*F(A)>0 then A:=M else B:=M;

until (F(M)=0) or (abs(B-A)<E);

writeln ('la soluzione S',M:12:8,'errore massimo',E:12:8)

end.

Diagramma di flusso per la risoluzione dell'equazione F(X)=0 con il metodo della bisezione.

---