|
|
| |
CORRELACIONES
Con el programa SPSS
se pueden calcular correlaciones paramétricas y no paramétricas entre
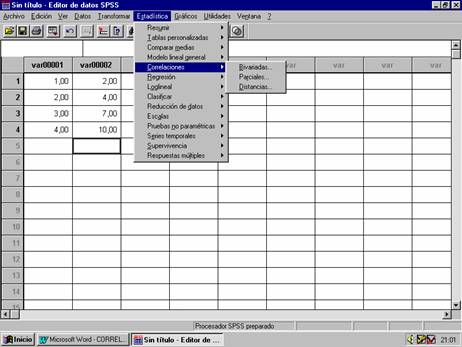
variables, así como correlaciones parciales. Para ello pinchar en el menú Estadística
y seleccionar la opción Correlaciones,
es decir:
1. Correlaciones Bivariadas
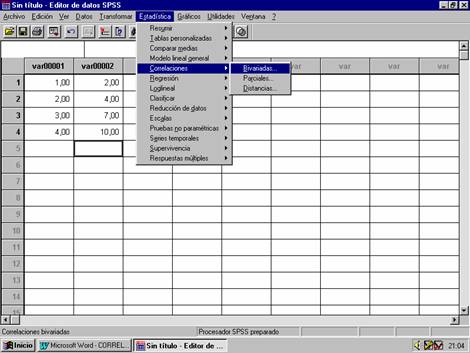
Si se desea calcular
el coeficiente de correlación entre 2 variables hay que seleccionar la opción Bivariadas. y aparecerá la siguiente
ventana:
En el campo Variables: se debe incluir la lista de variables sobre las que se quiere calcular la matriz de correlación
En el campo de Coeficientes de correlación se selecciona el coeficiente que se desea obtener.
En el campo de Prueba de significación se selecciona si se desea obtener el test bilateral o unilateral.
Si se pincha en el botón de Opciones... aparece la siguiente ventana:
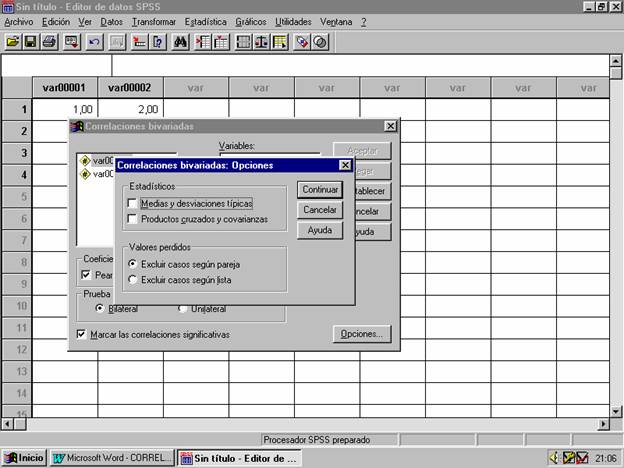
Que permite obtener,
además de la matriz de correlación, las medias y desviaciones típicas, y la
matriz de varianzas y covarianzas. En el campo de Valores perdidos se indica la forma de eliminar casos en los
cálculos de la matriz de correlación, es decir, si se selecciona la opción de Excluir casos según pareja (esto es lo
que ocurre por defecto), se eliminarán aquellos casos que sean missing en alguna de las 2 variables
para las que se calcula la correlación, y si se selecciona la opción Excluir casos según lista, se
eliminarán aquellos casos que sean missing
en alguna de las variables para las que se va a calcular la matriz de
correlación.
comandos del SPSS/PC: Comando CORRELATIONS y NONPAR CORR
En las versiones del SPSS/PC para MSDOS, este análisis se realiza utilizando el comando CORRELATIONS para obtener la correlación de Pearson, y el comando NONPAR CORR para obtener la de Spearman y la Tau-b de Kendall. La sintaxis de estos comandos es:
CORRELATIONS [VARIABLES=] varlist [WITH varlist] [/varlist...]
[/MISSING= [INCLUDE]]
[/PRINT= ]
[/MATRIX=OUT(file)]
[/STATISTICS=[DESCRIPTIVES][XPROD][ALL]]
**Default if the subcommand is omitted.
Default for /MATRIX OUT is the working data file.
NONPAR CORR [VARIABLES=] varlist [WITH varlist] [/varlist...]
[/PRINT=]
[/SAMPLE]
[/MISSING=] [INCLUDE]
[/MATRIX=OUT(file)]
**Default if the subcommand is omitted.
Default for /MATRIX OUT is the working data file.
Interpretación de resultados
Supongamos que se va a calcular la matriz de correlación entre las siguientes variables: EDAD (edad del sujeto), TTRABAJA (número de meses trabajando en el último empleo) y TBUSCA (número de meses que lleva buscando empleo). Se solicita también las medias y desviaciones, y la matriz de varianza-covarianza. Utilizar en el análisis aquellos casos que no sean missing en las tres variables a la vez.
EDAD TBUSCA TTRABAJA
EDAD 1,0000 ,1045 ,3021
( 84) ( 84) ( 84)
P= , P= ,344 P= ,005
TBUSCA ,1045 1,0000 ,2055
( 84) ( 84) ( 84)
P= ,344 P= , P= ,061
TTRABAJA ,3021 ,2055 1,0000
( 84) ( 84) ( 84)
P= ,005 P= ,061 P= ,
COMENTARIO: Esta salida nos da: el coeficiente de correlación, el tamaño muestral y un p-valor. El
p-valor viene asociado a un contraste de hipótesis H0: R = 0; H1: R <> 0; Es decir si R2=0 el intervalo de confianza asociado a R, contiene a 0, lo cual significa que tiene valores negativos y positivos, lo cual implica que no podemos asegurar si la asociación es positiva o negativa "A medida que crece una variable, la otra crece? O decrece?". Por tanto podemos asegurar que las variables son independientes.
Si el p < 0.05, aceptamos la hipótesis nula, el cero no está contenido en el intervalo de confianza asociado a R, ese intervalo de confianza será siempre positivo o negativo y podremos asegurar que hay
asociación positiva o negativa, además ese coeficiente de correlación será válido (por bajo que sea "Hay poca asociación, pero podemos asegurar que hay asociación").
2. Correlaciones Parciales
Si se desea calcular la correlación parcial entre 2 variables, en el menú Estadística hay que seleccionar la opción Correlaciones y dentro de ésta pinchar en la opción Parciales. , es decir:
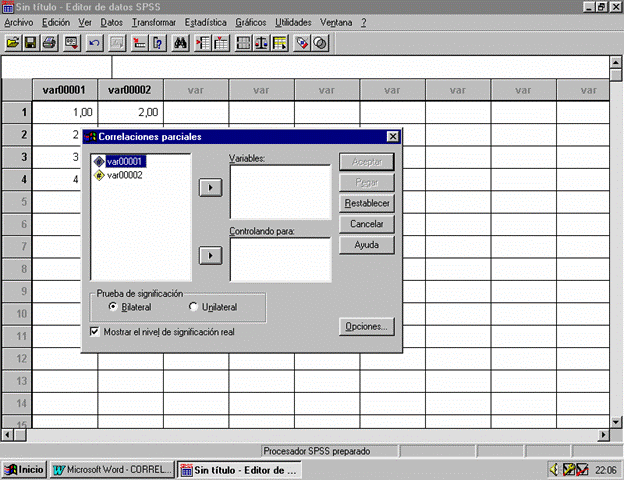
Entonces aparece la
siguiente ventana:
En el campo Variables se incluyen los nombres de las variables para las que se quiere calcular el coeficiente de correlación parcial.
En el campo Controlar para se incluyen los nombres de las variables de las que se va a eliminar la influencia. Por ejemplo, para calcular el coeficiente de correlación parcial entre x1 y x2 tras suprimir las influencias de x3 y x4, se incluyen las variables x1 y x2 en el campo Variables, y las variables x3 y x4 en el campo Controlar para.
En el campo de Prueba de significación se selecciona si se desea obtener el test bilateral o unilateral.
Si se pincha en el botón de Opciones... aparece la siguiente ventana:
Que permite obtener, además de la matriz de correlación, las medias y desviaciones típicas, y la matriz de correlaciones entre todas las variables. En el campo de Valores perdidos se indica la forma de eliminar casos en los cálculos de la matriz de correlación, es decir, si se selecciona la opción de Excluir casos según pareja (esto es lo que ocurre por defecto), se eliminarán aquellos casos que sean missing en alguna de las 2 variables para las que se calcula la correlación, y si se selecciona la opción Excluir casos según lista, se eliminarán aquellos casos que sean missing en alguna de las variables para las que se va a calcular la matriz de correlación.
Comando del SPSS/PC: Comando PARTIAL CORR
Este análisis se realiza utilizando el comando PARTIAL CORR, cuya sintaxis es:
PARTIAL CORR [VARIABLES=] varlist [WITH varlist] BY control list (levels)
[/varlist...]
[/SIGNIFICANCE=]
[/STATISTICS=[NONE**][CORR] ] [DESCRIPTIVES][BADCORR][ALL]
[/FORMAT=]
[/MISSING=[]]
[/MATRIX=[NONE**][IN(file)][OUT(file)]]
**Default if the subcommand is omitted.
Default for /MATRIX IN and OUT is the working data file.
Interpretación de resultados
- - - P A R T I A L C O R R E L A T I O N C O E F F I C I E N T S - - -
Controlling for.. TBUSCA
EDAD TTRABAJA
EDAD 1,0000 ,2819
( 0) ( 78)
P= , P= ,011
TTRABAJA ,2819 1,0000
( 78) ( 0)
P= ,011 P= ,
(Coefficient / (D.F.) / 2-tailed Significance)
Comentario: Las correlaciones parciales son correlaciones quitando el efecto de terceras variables. El típico caso es el de estar muy bien correlado el incremento de la esperanza de vida de los niños en USA a principios de siglo con la producción de carbón en Inglaterra por las mismas fechas. No tiene nada que ver pero están muy bien correladas. Ocurre que una tercera variable, en este caso el tiempo, está muy bien correlado con ambas, una vez quitado el efecto del tiempo, la correlación parcial entre las dos variables anteriores es paupérrima.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026