FUNZIONI - (funzione tale che ad x appartenente all'insieme A associa y appartenente all'insieme B)

informatica

FUNZIONI

Dati due insiemi A e B, quando ad un elemento del primo ne corrisponde uno del secondo abbiamo una funzione univoca.

F : x Є A y Є B

(funzione tale che ad x appartenente all'insieme A associa y appartenente all'insieme B)

Una generica funzione è indica con la scrittura  y = f(x); x è detta variabile indipendente, y variabile dipendente.

L'insieme delle x è detto dominio o insieme di definizione.

L'insieme delle y è detto codominio o insieme dei valori o insieme delle immagini .

Una qualunque funzione di variabile reale può essere rappresentata graficamente.

Il grafico della funzione è l'insieme delle coppie (x ; y) riportato in un piano cartesiano.

Una funzione si dice iniettiva o IN se a valori distinti della x corrispondono valori distinti della y

Ogni elemento del secondo insieme è immagine al più di un elemento del primo.

Graficamente ogni retta parallela all'asse delle x incontra il diagramma della funzione al più in punto (può anche non incontrarla)

y

x

Una funzione si dice suriettiva o SU se ogni elemento del secondo insieme è immagine di almeno un elemento del primo.

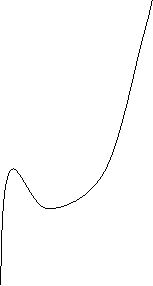Graficamente ogni retta parallela all'asse delle x incontra il diagramma della funzione almeno in un punto (deve per forza incontrarla almeno in un punto).

y

X

Se una funzione è sia iniettiva che suriettiva allora essa è detta biettiva o biunivoca. Ad ogni elemento del secondo insieme ne corrisponde uno del primo e viceversa.

Graficamente ogni retta parallela all'asse delle x incontra il diagramma della funzione in uno ed un sol punto.

Y

X

Se una funzione è biettiva essa è invertibile. Due funzioni una inversa dell'altra sono simmetriche rispetto alla retta y=x

Esempio:

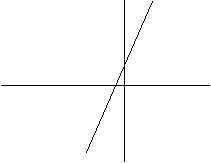
y = 2x+1 (1) Per calcolare l'inversa ricaviamo dall'equazione la x

2x = y-1

x = y-1

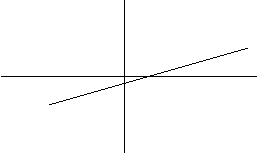
Scriviamo l'equazione nella forma    y = x-1  

2

Grafico della (1) Grafico della (2)