|
|
| |
FISICA I
(docente Maria Adele Dodero
Testo di riferimento
Fisica 1 (Raymond A. Serway)
Lezione 1 (22 settembre 1999)
Introduzione al corso: prerequisiti richiesti, programma, modalità d'esame, ecc..
Lezione 2 (27 settembre 1999)
La fisica è una "scienza sperimentale".
Le sue leggi sono infatti state "verificate" tramite degli opportuni esperimenti (riproducibili da chiunque si ponga nelle condizioni idonee).
Per studiare un fenomeno fisico occorre prima di tutto effettuare una osservazione di tipo "qualitativo" (es. "un corpo privato di sostegno cade verso terra"), poi occorre considerare quali "grandezze fisiche" caratterizzano il fenomeno (es. "velocità", "massa", ecc.), in quale "misura" e in che modo queste grandezze interagiscono fra loro.
Misura di grandezze fisiche
Misurare una grandezza fisica significa effettuare un "confronto" fra la grandezza da misurare e un "campione", opportunamente scelto, in modo da stabilire una corrispondenza univoca tra la grandezza stessa e un "numero" che ne rappresenta la "misura" nell'unità di misura prescelta.
N.B. Una misura ha significato solo se si specifica l'unità di misura presa in considerazione.
Dal momento che la precisione di una misura è sempre limitata (dipende dalla precisione dello strumento utilizzato, dalla tecnica con la quale si esegue la misura e dalla possibilità, sempre presente di errori accidentali) bisognerebbe sempre associare, ad ogni misura, il relativo "errore".
Leggi fisiche
Definire una "legge fisica" significa individuare le relazioni che legano fra loro le varie grandezze fisiche che compaiono nel fenomeno.
N.B. Dal momento che tutte le misure delle grandezze effettuate contengono degli errori il risultato ottenuto con l'applicazione della legge fisica conterrà a sua volta degli errori (in base alla "legge di propagazione degli errori").
Visto che, in base a quanto detto sopra, le grandezze fisiche non sono "indipendenti", ma collegate fra loro, è possibile scegliere un numero minimo di grandezze fisiche indipendenti ed esprimere tutte le altre in funzione di quelle prescelte.
Nel campo della "fisica meccanica" sono state scelte tre grandezze fisiche indipendenti fondamentali: lunghezza, massa e tempo (indicati rispettivamente con L, M e T).
Per quantificare queste grandezze si utilizzano comunemente le unità di misura del Sistema Internazionale (S. I.) e cioè il metro (m.), il chilogrammo (Kg.), e il secondo (s.).
|
In precedenza venivano utilizzati anche altri due "sistemi di misura": il sistema M. K. s. (cioè metro, chilogrammo e secondo) il sistema c. g. s. (cioè centimetro, grammo e secondo) Nota Il S. I. si differenzia dal sistema M. K. s. in quanto comprende anche l'unità di misura di una quarta grandezza fisica fondamentale (presente nello studio dell'elettromagnetismo): l'intensità di corrente che viene misurata in ampere (A.). |
Equazioni dimensionali
Di ogni grandezza fisica è possibile dare una "equazione dimensionale", cioè un'equazione che esprima la grandezza fisica presa in considerazione in "funzione" di L, M e T.
Esempi
la velocità è una
grandezza fisica derivata che si esprime in funzione dello spazio percorso e
del tempo impiegato: ![]()
l'accelerazione, a
sua volta, può essere ricavata dalla velocità: ![]()
Nella formulazione di una "legge fisica" bisogna tenere conto della "omogeneità dimensionale", cioè le equazioni dimensionali dei due membri dell'equazione che esprime la legge stessa devono essere equivalenti (in caso contrario significa che sono presenti degli errori).
![]()
![]()
Esempio: h(t) = h0 - ½gt2 [L] = [L] - [L T-2] T2 [L] = [L]
(da notare che il valore ½ è un numero e, quindi, "adimensionale" )
Grandezze fisiche "scalari" e "vettoriali"
Le grandezze fisiche possono essere di due tipi:
scalari sono le grandezze per le quali è sufficiente conoscerne il valore nell'unità di misura prescelta (es. tempo, temperatura, ecc.);
vettoriali sono le grandezze individuate tramite l'utilizzo di un "vettore", cioè quelle grandezze per le quali occorre definire, oltre al modulo, anche una direzione e un verso (es. velocità, spostamento, accelerazione, ecc.).
C I N E M A T I C A
La cinematica è la parte della fisica che studia il movimento dei corpi (senza però occuparsi delle cause che hanno prodotto il movimento stesso, che sono invece oggetto di studio della "dinamica").
Cinematica del punto
Per studiare il movimento di un corpo è necessario avere a disposizione:
un sistema di "coordinate spaziali" (es. coordinate cartesiane (x, y, z) con i versori associati![]()
un "orologio" (per misurare gli intervalli di tempo).
Studiare il movimento di un corpo significa, infatti, studiare la sua posizione, nelle coordinate considerate, rispetto al tempo.
Un oggetto è considerato un "punto materiale" quando le sue dimensioni possono essere trascurate, cioè quando le sue dimensioni sono molto più piccole (come ordine di grandezza) rispetto alle dimensioni del problema che sto considerando.
Non è quindi importante considerare le dimensioni "assolute" dell'oggetto considerato, ma le sue dimensioni "relative" all'interno del contesto preso in esame.
Moti unidimensionali (moto rettilineo)
Nello studio del moto rettilineo è
sufficiente utilizzare un solo asse coordinato (ad esempio l'asse x). In questo
caso le grandezze vettoriali (spostamento, velocità e accelerazione) avranno la
stessa direzione del versore ![]() . Possiamo quindi effettuare i calcoli tenendo conto solo del
"modulo".
. Possiamo quindi effettuare i calcoli tenendo conto solo del
"modulo".
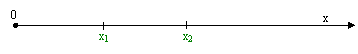
Supponiamo che sia: x1 = posizione dell'oggetto all'istante t1
x2 = posizione dell'oggetto all'istante t2
Definizione: Definiamo
"spostamento" del corpo lo spazio percorso
dallo stesso nell'intervallo di tempo (![]() ) e lo indichiamo con
) e lo indichiamo con ![]() .
.
Questo spostamento può essere positivo (x2
> x1) se si tratta di un "moto progressivo", cioè che avviene
nello stesso verso di ![]() , oppure negativo (x2 < x1) se si
tratta di un "moto regressivo".
, oppure negativo (x2 < x1) se si
tratta di un "moto regressivo".
Definizione: Definiamo
"velocità media" di un corpo il rapporto tra lo
spazio percorso e il tempo impiegato a percorrerlo: ![]() .
.
La velocità media non fornisce però un'informazione "reale", ma solo un'indicazione "media".
Per ottenere informazioni più precise occorre restringere gli intervalli di tempo considerati. Supponendo di arrivare a intervalli di tempo infinitesimali otteniamo:
Definizione: "Velocità istantanea": ![]()
Supponiamo ora che sia: v1 = velocità dell'oggetto all'istante t1
v2 = velocità dell'oggetto all'istante t2
Definizione: "Accelerazione media": ![]() (con Dv = v2 - v1)
(con Dv = v2 - v1)
Come nel caso della velocità media, anche l'accelerazione media non fornisce un'informazione reale. Per ottenere informazioni più precise occorre, anche in questo caso, restringere gli intervalli di tempo considerati. Supponendo quindi di arrivare a intervalli di tempo infinitesimali otteniamo:
Definizione: "Accelerazione istantanea": ![]() .
.
Possiamo considerare due tipi di "moto rettilineo":
a) Il moto rettilineo uniforme
b) Il moto rettilineo uniformemente accelerato
Nel primo caso la velocità si mantiene costante (sia in modulo che in direzione e verso) e quindi l'accelerazione è uguale a zero.
Questo è l'unico caso nel quale ciò è possibile. Infatti, negli altri casi, pur non variando il modulo, il vettore velocità non può essere costante in quanto varia la direzione e/o il verso e, di conseguenza, l'accelerazione è sempre diversa da zero.
Considerando quindi che v = v0 e a = 0, calcoliamo la "equazione oraria del moto", cioè la posizione dell'oggetto in funzione del tempo e della sua posizione iniziale:
![]() (con "c" costante
arbitraria).
(con "c" costante
arbitraria).
La costante arbitraria "c" deve essere valutata sulla base delle "condizioni iniziali". Se infatti, nell'equazione ottenuta, poniamo "t = 0", otteniamo "x = c". In pratica la costante rappresen 727h72h ta la posizione dell'oggetto nell'istante t0, cioè nell'istante iniziale.
Chiamando x0 la posizione iniziale dell'oggetto otteniamo quindi la seguente equazione oraria del moto rettilineo uniforme: x = x0 + v0 t.
Nel caso del moto rettilineo uniformemente accelerato, invece, è l'accelerazione a mantenersi costante. Operando in modo analogo al precedente possiamo quindi calcolare la relativa equazione oraria in funzione del tempo e della posizione e velocità iniziale di un oggetto:
![]() (con v0 =
velocità iniziale).
(con v0 =
velocità iniziale).
Dal momento che ![]() , possiamo sostituire questo valore nell'equazione precedente
ottenendo:
, possiamo sostituire questo valore nell'equazione precedente
ottenendo:
![]()
Chiamando nuovamente x0 la posizione iniziale dell'oggetto otteniamo l'equazione oraria del moto rettilineo uniformemente accelerato: x = x0 + v0 t + ½ a t2.
Lezione 3 (28 settembre 1999)
Riepilogo lezione precedente:
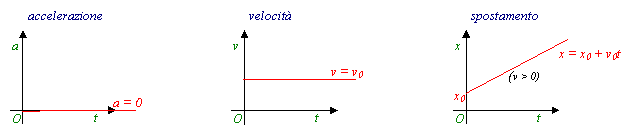 Moto rettilineo uniforme: a = 0 v = cost.
Moto rettilineo uniforme: a = 0 v = cost. ![]()
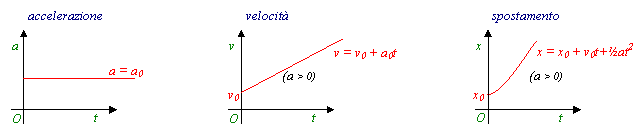 Moto rettilineo uniformemente
accelerato: a = cost v = v0 + at
Moto rettilineo uniformemente
accelerato: a = cost v = v0 + at ![]()
Prendendo in considerazioni le equazioni del moto rettilineo uniformemente accelerato è possibile esprimere la relazione tra lo spostamento e i valori di accelerazione, velocità iniziale e velocità finale (eliminando dall'equazione la variabile "tempo") nel seguente modo:
Dall'equazione ![]() possiamo
ricavare:
possiamo
ricavare: ![]()
![]()
![]()
![]()
![]() Sostituendo questo valore di "t" nell'equazione
Sostituendo questo valore di "t" nell'equazione ![]() si ottiene:
si ottiene: ![]() Quindi possiamo
affermare che:
Quindi possiamo
affermare che: ![]()
Osservazione
Occorre tenere presente che alcune delle grandezze fisiche considerate sono in realtà delle grandezze vettoriali. Finora abbiamo indicato solo i moduli di tali grandezze in quanto, trattandosi di un moto "rettilineo" non si hanno cambiamenti di direzione o verso dei relativi vettori.
In effetti però sarebbe più esatto indicare le grandezze considerate nel seguente modo:
Spostamento
lungo l'asse delle x: ![]()
Velocità
media: ![]() Velocità
istantanea:
Velocità
istantanea: ![]()
Accelerazione
media: ![]() Accelerazione
istantanea:
Accelerazione
istantanea: ![]()
Caduta libera dei gravi


![]() Un oggetto posto in
vicinanza della superficie terrestre è sottoposto ad un'accelerazione g, diretta secondo la verticale del luogo, che prende
il nome di "accelerazione di gravità" e ha un
valore di circa 9,8 m/s2.
Un oggetto posto in
vicinanza della superficie terrestre è sottoposto ad un'accelerazione g, diretta secondo la verticale del luogo, che prende
il nome di "accelerazione di gravità" e ha un
valore di circa 9,8 m/s2.
![]() In realtà anche il
modulo del vettore g non è costante, bensì
varia in base alla distanza. Anche in questa caso è comunque possibile
considerare questo valore costante per distanze molto piccole rispetto al
raggio terrestre.
In realtà anche il
modulo del vettore g non è costante, bensì
varia in base alla distanza. Anche in questa caso è comunque possibile
considerare questo valore costante per distanze molto piccole rispetto al
raggio terrestre.
N.B. L'accelerazione di gravità è una costante valida per ogni corpo in modo del tutto indipendente dalla sua "massa": due corpi lasciati cadere nel vuoto cadono esattamente alla stessa velocità.
(Le differenze di velocità osservate nella vita quotidiana sono dovute alla "resistenza" esercitata dall'aria).
Caduta di gravi Moto uniformemente accelerato
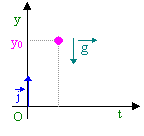 v0 =0 y0 = altezza iniziale
v0 =0 y0 = altezza iniziale
g = 9,8 m/s2 (![]() a = -
j)
a = -
j)
![]()
![]()
Il
tempo di caduta si ricava ponendo y = 0
nell'equazione (*): ![]() .
.
Conoscendo
t è possibile calcolare la velocità
dell'oggetto quando tocca il suolo: 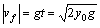 .
.
Nota: trasformazione tra km/h e m/s
![]()
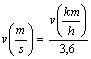 e
e ![]()
Moti curvilinei
![]()
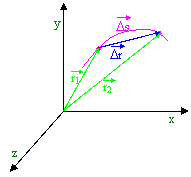 posizione del punto
materiale all'istante t1
posizione del punto
materiale all'istante t1
posizione del punto materiale all'istante t2
spostamento della particella lungo la traiettoria
(viene persa l'informazione relativa alla traiettoria effettiva)
traiettoria effettiva compiuta dal punto materiale
![]()
Per avere informazioni più dettagliate occorre "restringere" l'intervallo di tempo Dt
![]()
![]()
![]() dr ds
(spostamento infinitesimo lungo la traiettoria)
dr ds
(spostamento infinitesimo lungo la traiettoria)
La velocità istantanea ha direzione "tangente" alla traiettoria nel punto considerato.
![]() Possiamo pensare di
scomporre il vettore velocità indicandone separatamente il "modulo" e la
"direzione". Per far questo utilizziamo un "versore" ut
per indicare la direzione e il verso di v.
Possiamo pensare di
scomporre il vettore velocità indicandone separatamente il "modulo" e la
"direzione". Per far questo utilizziamo un "versore" ut
per indicare la direzione e il verso di v.
Riscriviamo quindi la formula di v nel seguente modo:![]() .
.
N.B. Un moto curvilineo è sempre "accelerato" in quanto la velocità varia sempre. Infatti anche quando il modulo resta costante, varia comunque la direzione.
L'accelerazione
![]()
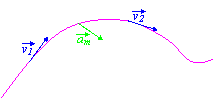 velocità del punto
all'istante t1
velocità del punto
all'istante t1
velocità del punto all'istante t2
![]()
Da notare che la direzione del vettore accelerazione è diretta sempre verso l'interno della curva.
Anche in questo caso, per avere informazioni più dettagliate occorre "restringere" l'intervallo Dt
Si ottiene così l'accelerazione
istantanea: ![]() .
.
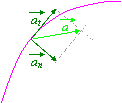 In
generale il vettore accelerazione è formato da due componenti (individuati
tramite la scomposizione secondo la regola del parallelogramma):
In
generale il vettore accelerazione è formato da due componenti (individuati
tramite la scomposizione secondo la regola del parallelogramma):
accelerazione tangenziale (direzione tangente alla curva)
accelerazione normale o centripeta (direzione ortogonale a quella dell'accelerazione tangenziale)
Lezione 4 (4 ottobre 1999)
 Ricavare le componenti "tangenziale" e "normale"
dell'accelerazione
Ricavare le componenti "tangenziale" e "normale"
dell'accelerazione
![]()
![]()
![]() Possiamo scrivere il
vettore velocità indicando separatamente la parte direzionale (versore ut) dalla parte di modulo (v). Scriveremo quindi: v
= ut v.
Possiamo scrivere il
vettore velocità indicando separatamente la parte direzionale (versore ut) dalla parte di modulo (v). Scriveremo quindi: v
= ut v.
![]()
![]()
![]()
![]() Calcoliamo la
derivata di ut rispetto a q (variazione del vettore ut al variare dell'angolo q
Calcoliamo la
derivata di ut rispetto a q (variazione del vettore ut al variare dell'angolo q
![]()
Da cui otteniamo: 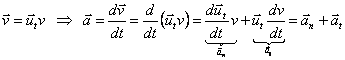
an = variazione della "direzione" della velocità
dq variazione dell'angolo formato dai due
versori ut con l'asse x. Si verifica che: a = dq (l'angolo fra i versori
normali è uguale a quello fra i vettori tangenziali) r raggio istantaneo di curvatura della
traiettoria (varia da punto a punto) Nota che, nel caso del moto rettilineo, si ha un raggio istantaneo
di curvatura della traiettoria " 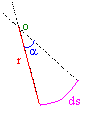
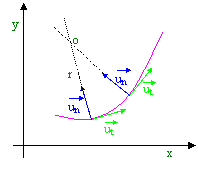 at = variazione del "modulo" della
velocità
at = variazione del "modulo" della
velocità
![]()
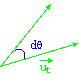
ds è uno "spostamento
infinitesimo" che approssima lo spostamento lungo la traiettoria "curvilinea",
abbiamo quindi: ![]()
![]() Possiamo ora calcolare la derivata di ut
rispetto al tempo:
Possiamo ora calcolare la derivata di ut
rispetto al tempo: ![]()
Otteniamo infine: ![]() .
.
Osservazione
L'accelerazione normale dipende dal raggio di curvatura della traiettoria e varia come v2.
La presenza di un'accelerazione implica la presenza di una "forza" che imprima l'accelerazione stessa facendo variare il modulo e/o la direzione del vettore velocità.
|
Schema riassuntivo |
||
|
Moto rettilineo uniforme |
at = 0 |
an = 0 |
|
Moti rettilinei non uniformi |
at |
an = 0 |
|
Moti curvilinei uniformi |
at = 0 |
an |
|
Moti curvilinei non uniformi |
at |
an |
Moto "piano" nel piano xy
Un qualunque moto piano può essere considerato come la composizione di due moti rettilinei.
Nel caso che consideriamo (piano xy) sarà la composizione di un moto lungo l'asse delle x e di uno lungo l'asse delle y.
Abbiamo dunque: ![]() e
e ![]()
Possiamo perciò applicare le formule già adoperate per i moti rettilinei:
![]() e
e ![]() per il moto
lungo l'asse delle x
per il moto
lungo l'asse delle x
![]() e
e ![]() per il moto lungo
l'asse delle y
per il moto lungo
l'asse delle y
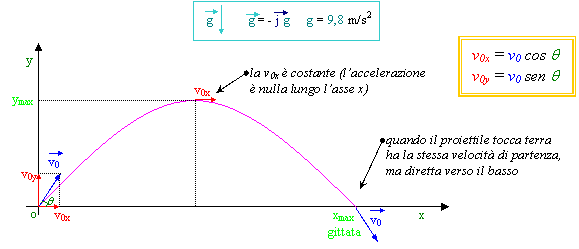 Moto del "proiettile"
Moto del "proiettile"
|
asse x |
asse y |
|
moto rettilineo uniforme ax = 0 vx = v0x = v0 cosq x = x0 + v0 cosq t |
moto rettilineo uniformemente accelerato ay = - g vy = v0 senq - g t y = y0 + v0 sen q t - ½ g t2 |
In ymax la velocità ha solo la componente orizzontale (v0x); la componente vy si è annullata per effetto dell'accelerazione negativa "- g".
Ponendo vy = 0
otteniamo: ![]()
Sostituendo nell'equazione della y il valore di t troviamo: (supponiamo y0 = 0)

![]()
Dal momento che la curva è simmetrica il tempo di
volo sarà esattamente (in assenza di attrito) il doppio del tempo necessario a
raggiungere ymax, cioè: ![]() ;
;
formula
di duplicazione del seno![]()
Risulta quindi immediato calcolare la gittata:
![]() ;
;
Possiamo inoltre determinare l'angolo per il quale si ottiene la massima gittata (a parità di altre condizioni): il valore "massimo" di xmax si ottiene quando sen 2q = 1, cioè quando q
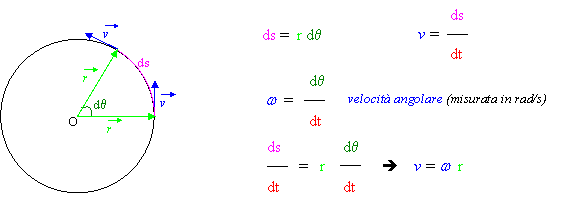 Moto circolare
Moto circolare
![]()
![]()
![]() La velocità angolare non è una grandezza scalare, ma
vettoriale; oltre a definirne il modulo occorre quindi indicarne anche la
direzione e il verso: la direzione è ortogonale al piano del movimento mentre
il verso è determinato secondo la "regola della mano destra" tenendo conto
della seguente relazione: v = w r (dove
il segno indica il prodotto vettoriale fra due vettori
La velocità angolare non è una grandezza scalare, ma
vettoriale; oltre a definirne il modulo occorre quindi indicarne anche la
direzione e il verso: la direzione è ortogonale al piano del movimento mentre
il verso è determinato secondo la "regola della mano destra" tenendo conto
della seguente relazione: v = w r (dove
il segno indica il prodotto vettoriale fra due vettori
Lezione 5 (5 ottobre 1999)
 Moto circolare uniforme
Moto circolare uniforme
Da notare che, essendo una circonferenza, il raggio è costante, quindi lo è anche l'accelerazione normale (e di conseguenza l'accelerazione totale).
Equazione oraria del moto circolare uniforme
Si tratta di calcolare l'angolo q in funzione del tempo.
Poniamo, come condizioni iniziali: t0 = 0 e q q
![]()
![]()
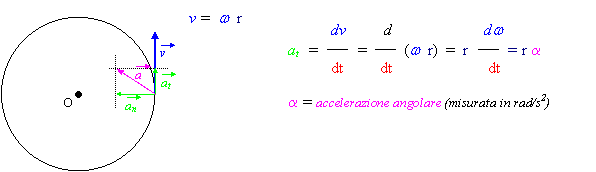 Moto circolare uniformemente accelerato
Moto circolare uniformemente accelerato
|
Schema riassuntivo |
||
|
|
RETTILINEO |
CIRCOLARE |
|
Moto uniforme |
x = x0 + v t |
q q w t |
|
Moto uniformemente accelerato |
v = v0 + a t x = x0 + v0 t + ½ a t2 |
w w a t * q q w t + ½ a t2 ** |
* Condizioni iniziali: t0 = 0; w w ![]()
Condizioni iniziali:
t0 = 0; q q ![]()
Moto circolare e oscillazioni armoniche

Se esaminiamo le proiezioni sull'asse x delle varie posizioni del punto (A', B', ecc.) ci accorgiamo che la "x" oscilla fra "- r" e "r" mentre il punto compie la sua traiettoria circolare.
Osserviamo che: A' = r cos q = r cos w t.
![]()
In generale possiamo affermare che: x = x0 cos (w t + q
Questa equazione rappresenta il moto di un punto materiale che oscilla da "- x0" a "x0".
In questo caso la w prende il nome di "pulsazione del moto armonico".
![]()
Si ottiene un risultato analogo considerando le proiezioni sull'asse y: y = y0 sen (w t + q
Definiamo "periodo" (che indichiamo con " T ") il tempo impiegato dalla particella ad effettuare un movimento periodico completo (da - x0 a x0 e ritorno).
![]() tempo impiegato per compiere un
intero giro (moto circolare)
tempo impiegato per compiere un
intero giro (moto circolare)
T
tempo impiegato per compiere un'oscillazione completa (moto oscillatorio)

Se il moto è uniforme, si
ha: ![]() , cioè:
, cioè: ![]() da cui
otteniamo: T
=
da cui
otteniamo: T
= ![]()
Definiamo "frequenza" (che indichiamo con " f ") l'inverso del periodo: f = ![]()
La frequenza indica quanti giri (nel caso di moto circolare) o quante oscillazioni complete (nel caso di moto oscillatorio) vengono effettuate in un secondo. Si misura in "hertz" ( 1 hz = 1 s-1).
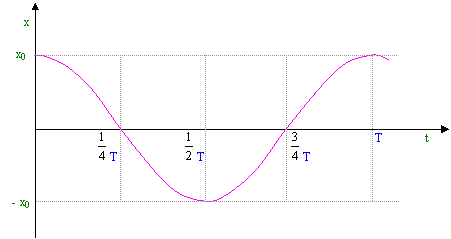 Poniamo q e consideriamo x = x0 cos (w t + q
Poniamo q e consideriamo x = x0 cos (w t + q
Per t = 0 abbiamo x = x0 (il corpo parte alla massima distanza dall'origine).
Consideriamo ora la
velocità: ![]()
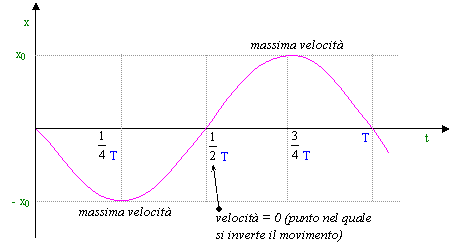 La quantità " w x0
"
prende il nome di "ampiezza della velocità" e
dipende dall'ampiezza dell'oscillazione ( x0 ) e dalla pulsazione
del moto armonico ( w
La quantità " w x0
"
prende il nome di "ampiezza della velocità" e
dipende dall'ampiezza dell'oscillazione ( x0 ) e dalla pulsazione
del moto armonico ( w
Osserviamo che: ![]()
L'accelerazione è proporzionale allo spostamento x, quindi anche la forza che causa l'accelerazione dovrà essere proporzionale a x. Inoltre questa forza tende a riportare l'oggetto nella posizione di "equilibrio" centrale. Per questo viene definita come "forza di richiamo".
Equazione differenziale del moto armonico
![]()
 Considerando che
Considerando che ![]() , possiamo dire che un'equazione differenziale del secondo
ordine del tipo
, possiamo dire che un'equazione differenziale del secondo
ordine del tipo ![]() avrà come
soluzione:
avrà come
soluzione: ![]() .
.
RELATIVITA' GALILEIANA
Ci poniamo il problema di come legare le varie grandezze fisiche nei diversi sistemi di riferimento. Ogni fenomeno, infatti, "appare" in modo diverso in base al sistema di riferimento considerato.
La "relatività galileiana" si basa su due postulati fondamentali:
Gli intervalli di tempo sono gli stessi, misurati nei diversi sistemi di riferimento (Dt = Dt');
Le lunghezze sono uguali, misurate in tutti i sistemi di riferimento (l = l').
Queste considerazioni sono valide solo per oggetti che abbiano una velocità molto inferiore a quella della luce (fino a un valore v = 0,1 0,2 C con C = velocità della luce = 3 108 m/s).

![]() Per la regola della
somma fra vettori si ha:
Per la regola della
somma fra vettori si ha: ![]() quindi:
quindi: ![]() da cui:
da cui: ![]()
con v = velocità nel sistema di riferimento o e v' = velocità nel sistema di riferimento o' .
Per quanto riguarda l'accelerazione possono verificarsi due diversi casi:
Il sistema o' si muove con velocità uniforme vR rispetto al sistema o
![]() da cui, visto che
da cui, visto che ![]() si ricava:
si ricava: ![]()
Nei due sistemi si ha la stessa "legge del moto".
Il sistema o' si muove rispetto al sistema o con velocità vR non costante
![]() da cui otteniamo:
da cui otteniamo: ![]()
L'accelerazione non è la stessa in tutti i sistemi di riferimento. Nel sistema di riferimento o' possono esserci delle accelerazioni dipendenti da aR che vengono chiamate anche "accelerazioni fittizie" in quanto non provocate dall'azione di nessuna forza (v. esempio del tram che frena).
Lezione 6 (11 ottobre 1999)
Le trasformazioni di Galileo furono messe in crisi da esperimenti effettuati nell'Ottocento con i quali si dimostrò che la luce si propaga nel vuoto sempre alla stessa velocità in qualunque sistema di riferimento. L'errore è dovuto proprio ai due postulati. Ad altissime velocità (prossime a quelle della luce) si ha una "dilatazione dei tempi" e una "contrazione delle lunghezze".
D I N A M I C A
La dinamica è la parte della fisica che studia le cause che producono il movimento dei corpi.
Le leggi della dinamica di Newton
C = velocità della luce m = massa di riposo
La
dinamica classica (di Newton) si basa sull'ipotesi che la massa inerziale di un
corpo sia costante (indipendentemente dalla sua velocità). In realtà, secondo
la teoria relativistica, la massa di un corpo dipende dalla sua velocità nel
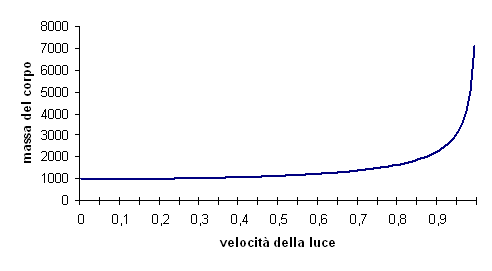
seguente modo:
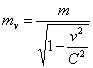
Se poniamo v = 0,1 C otteniamo: 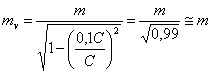 .
.
Risulta
evidente, tanto dal grafico quanto dalla formula, il motivo per il quale
nessun corpo materiale può essere accelerato ad una velocità pari a quella
della luce. Infatti se v = C si annulla il denominatore
della frazione quindi la massa tende all'infinito.
Risulta
quindi evidente che, per valori molto inferiori alla velocità della luce, è
possibile considerare la massa come se fosse costante e applicare le leggi
della dinamica di Newton.
Dinamica classica
La dinamica classica si prefigge lo scopo di scoprire le cause che determinano una "accelerazione" nei corpi causandone il movimento o, al contrario, arrestandone il moto.
Queste "cause" prendono il nome di "forze" e sono determinate dalle interazioni fra i corpi.
LE TRE LEGGI DELLA DINAMICA DI NEWTON
I) PRINCIPIO D'INERZIA
Un corpo permane nel suo stato di quiete o di moto rettilineo e uniforme fino a che non intervenga una causa (forza) esterna a modificare questo stato di quiete o di moto rettilineo e uniforme.
(Nota: lo stato di quiete è un particolare stato di moto rettilineo e uniforme con v costante = 0).
In un "sistema accelerato" non vale il principio d'inerzia: lo stato di un corpo può cambiare anche senza che si verifichi alcuna interazione fra i corpi (v. esempio del tram).
Un sistema di riferimento viene definito "sistema di riferimento inerziale" se è possibile verificare che in quel particolare sistema di riferimento è valido il principio d'inerzia (almeno nei confronti del tipo di esperimento che si intende effettuare). Il pianeta terra, per esempio, può essere considerato un sistema inerziale per certi esperimenti (ad esempio oscillazione del pendolo in un periodo di tempo relativamente breve) e non per altri (ad esempio oscillazione del pendolo in un periodo di tempo relativamente lungo: v. esperimento del pendolo di Foucault).
Osservazione
Se un sistema di riferimento è inerziale allora tutti i sistemi di riferimento che si muovono con velocità costante (moto rettilineo e uniforme) rispetto ad esso sono sistemi di riferimento inerziali.
Massa inerziale
Definiamo "massa" (inerziale) di un oggetto l'inerzia che ha l'oggetto stesso a cambiare il suo stato di quiete o di moto rettilineo e uniforme. Quando si applica una "forza" a un oggetto questo acquista un'accelerazione che è "inversamente proporzionale" alla sua massa inerziale. A parità di forza applicata, quindi, un oggetto con massa inerziale maggiore acquisterà un'accelerazione minore di uno con massa inerziale inferiore.

Per misurare la massa si utilizza una "massa
campione". Si applica la stessa forza sia alla massa campione che a quella in
esame. Si misurano le accelerazioni ottenute e si ricava il valore della massa
cercata nel seguente modo: ![]() (mc e ac
indicano rispettiv. massa e accelerazione del campione).
(mc e ac
indicano rispettiv. massa e accelerazione del campione).
Inoltre si verifica sperimentalmente che l'accelerazione acquistata dal corpo ha la stessa direzione e lo stesso verso della forza applicata. Anche la forza, infatti, è una grandezza vettoriale.
II) SECONDA LEGGE DELLA DINAMICA
La seconda legge della dinamica è una diretta conseguenza di quanto appena detto.
La forza applicata ad un corpo di massa "m" è
uguale al prodotto della massa per l'accelerazione acquistata dal corpo. In
pratica si ha: ![]() .
.
Se ad un corpo si applicano più forze per
ognuna è valida la legge di Newton. L'accelerazione acquistata dal corpo è
determinata dalla "risultante" di tutte le forze applicate: ![]() .
.
Ovviamente se si ha un "equilibrio di forze", cioè se la risultante delle forze applicate è "nulla" si avrà un'accelerazione uguale a zero.
III) PRINCIPIO DI AZIONE E REAZIONE

F12 è la forza esercitata da m2 su m1 (agisce su m1)
F21 è la forza esercitata da m1 su m2 (agisce su m2)
Il principio di "azione e reazione" afferma che queste due forze sono uguali in modulo e direzione, ma hanno verso opposto: F12 = - F21.
FORZA PESO
![]()
![]()
![]()
![]()
![]()
 P = m g g = 9,8 m/s2 =
accelerazione di gravità (forza con la quale la Terra e un oggetto si
attraggono).
P = m g g = 9,8 m/s2 =
accelerazione di gravità (forza con la quale la Terra e un oggetto si
attraggono).
![]()
La forza è una grandezza fisica "derivata".
"Equazione dimensionale": [F] = [M] [a] = [M L T-2]
Nel sistema MKS (normalmente utilizzato) si ha: F = Kg m s-2 = 1 N (newton)
Nel sistema CGS (ormai in disuso) si ha: F = gr cm s-2 = 1 d (dina)
QUANTITA' DI MOTO
Definiamo "quantità di moto" di un oggetto il prodotto della sua massa per la velocità.
 p = m v p è parallelo al vettore
velocità e quindi tangente in ogni punto alla traiettoria percorsa
p = m v p è parallelo al vettore
velocità e quindi tangente in ogni punto alla traiettoria percorsa
Se ci troviamo in un sistema isolato come quello considerato in precedenza, abbiamo:
![]() e
e ![]() da cui, per il
"principio di azione e reazione" si ha:
da cui, per il
"principio di azione e reazione" si ha: ![]()
Si verifica uno "cambio di quantità di moto": la quantità di moto persa (o guadagnata) dall'oggetto uno viene guadagnata (o persa) dall'oggetto due.
Osserviamo anche che: ![]() la somma delle
quantità di moto non varia rispetto al tempo (derivata nulla) quindi possiamo
affermare che:
la somma delle
quantità di moto non varia rispetto al tempo (derivata nulla) quindi possiamo
affermare che: ![]() è costante.
è costante.
Principio di conservazione della quantità di moto
In un sistema isolato la quantità di moto è costante. Infatti l'esempio da noi considerato su un sistema isolato di soli due oggetti, può essere esteso al caso di un sistema isolato di "n particelle".
Si avrà quindi: ![]() (quantità di moto
totale del sistema).
(quantità di moto
totale del sistema).
Attenzione! La quantità di moto delle singole particelle può variare (e in generale varia). È solo la quantità di moto totale a rimanere costante.
Esempio
![]() Un fucile di massa mf
= 5 Kg spara un proiettile di massa mp = 20 gr a una velocità vp = 100 m/s.
Un fucile di massa mf
= 5 Kg spara un proiettile di massa mp = 20 gr a una velocità vp = 100 m/s.
Calcolare la velocità di rinculo del fucile.
![]()
![]()
![]()
![]()
![]() Condizione
iniziale: pf + pp
= 0 Condizione
finale: pf + pp =
0
Condizione
iniziale: pf + pp
= 0 Condizione
finale: pf + pp =
0
![]() m/s (con verso opposto rispetto a vp).
m/s (con verso opposto rispetto a vp).
Lezione 7 (12 ottobre 1999)
Vincoli: forze vincolari

N = "reazione del vincolo": forza esercitata dal piano sul blocco.
(all'interno del piano sono presenti delle "forze molecolari" che a loro volta controbilanciano la forza N evitando che il piano si deformi).


![]()
![]()
![]() Se invece ci si
trova su un piano inclinato bisogna scindere la forza P
nelle sue due componenti Pn e Pt. In questo caso non si avrà più N = P, bensì N = Pn.
Se invece ci si
trova su un piano inclinato bisogna scindere la forza P
nelle sue due componenti Pn e Pt. In questo caso non si avrà più N = P, bensì N = Pn.
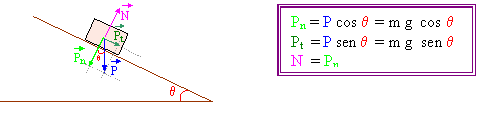
![]() In questo caso la forza con la quale il blocco
schiaccia il piano non è più la forza peso, ma solo la sua componente "normale"
rispetto al piano (Pn).
In questo caso la forza con la quale il blocco
schiaccia il piano non è più la forza peso, ma solo la sua componente "normale"
rispetto al piano (Pn).
![]()
![]()
![]() Non solo il modulo,
ma anche la direzione di N è uguale alla
direzione di Pn (ovviamente con
verso opposto) e non a quella di P.
Non solo il modulo,
ma anche la direzione di N è uguale alla
direzione di Pn (ovviamente con
verso opposto) e non a quella di P.
![]()
![]()
La componente normale del peso è equilibrata dalla reazione del vincolo: Pn + N = 0.
![]() La componente Pt invece tende ad accelerare il corpo
lungo la direzione del piano.
La componente Pt invece tende ad accelerare il corpo
lungo la direzione del piano.
![]()
![]() In assenza di forze
frenanti (forze di attrito) si ha: Pt = m a, da cui: a = g sen q
In assenza di forze
frenanti (forze di attrito) si ha: Pt = m a, da cui: a = g sen q
![]() L'angolo q è l'angolo formato dal piano sul quale scorre il blocco rispetto alla
direzione orizzontale (su un piano orizzontale si ha quindi a = g
sen 0 = 0 non si ha alcuna accelerazione dovuta
all'azione della forza peso). All'aumentare dell'angolo q si ha un aumento
del modulo della componente Pt e,
di conseguenza, un aumento dell'accelerazione e una diminuzione della forza con
la quale il blocco schiaccia il piano (caso limite: piano verticale q = 90° a = g e N = 0).
L'angolo q è l'angolo formato dal piano sul quale scorre il blocco rispetto alla
direzione orizzontale (su un piano orizzontale si ha quindi a = g
sen 0 = 0 non si ha alcuna accelerazione dovuta
all'azione della forza peso). All'aumentare dell'angolo q si ha un aumento
del modulo della componente Pt e,
di conseguenza, un aumento dell'accelerazione e una diminuzione della forza con
la quale il blocco schiaccia il piano (caso limite: piano verticale q = 90° a = g e N = 0).
I VINCOLI PIU' FREQUENTI
FILO
Esaminiamo il caso di un oggetto appeso ad un filo "inestensibile" (cioè che non si allunga quando vi si appende un oggetto) a sua volta fissato a un piano indeformabile.
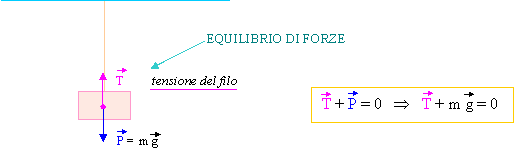
Esaminiamo ora quali forze agiscono nel filo:

La tensione applicata dal blocco al filo si trasmette al soffitto: un filo inestensibile di massa trascurabile trasmette semplicemente la tensione da un punto ad un altro.
Per ogni forza si può identificare una "azione" e una corrispondente "reazione" (uguale e contrario secondo il terzo principio della dinamica). Non sempre però ci interessa conoscerle entrambe.
Nel caso del filo attaccato al soffitto, per esempio, non ci interessa la forza di reazione esercitata dalle forze molecolari presenti all'interno della struttura del soffitto che ne impediscono la deformazione o il crollo.
GUIDA CIRCOLARE ORIZZONTALE
 Esaminiamo il caso
di un oggetto che si muove all'interno di una "guida circolare" posta su un
piano orizzontale. Il corpo è vincolato dalla presenza della guida a compiere
un percorso circolare.
Esaminiamo il caso
di un oggetto che si muove all'interno di una "guida circolare" posta su un
piano orizzontale. Il corpo è vincolato dalla presenza della guida a compiere
un percorso circolare.
Supponiamo inoltre che la guida sia "indeformabile".
LE FORZE DI ATTRITO
Fino ad ora abbiamo sempre considerato delle superfici perfettamente "lisce" che non opponessero nessuna resistenza al movimento degli oggetti.
Nella realtà però ciò non accade mai a causa della presenza delle "forze di attrito".
Se immaginiamo di appoggiare un oggetto su un piano e poi di inclinare gradualmente il piano stesso vediamo che il corpo non si mette in movimento fino a quando non raggiungiamo un certo angolo di inclinazione (che varia in base alle caratteristiche del piano e dell'oggetto).
Fino a quando il corpo non si mette in movimento significa che la componente Pt della forza peso (quella che dovrebbe determinare l'accelerazione del corpo) è esattamente equilibrata dalle "forze di attrito". In questo caso si parla di "attrito statico di strisciamento", cioè di un attrito che si manifesta su un oggetto fermo quando cerchiamo di metterlo in movimento facendolo strisciare.
La forza di attrito non è costante: aumenta proporzionalmente alla forza applicata fino a quando non si raggiunge una situazione di "attrito massimo" oltre la quale il corpo inizia a muoversi.
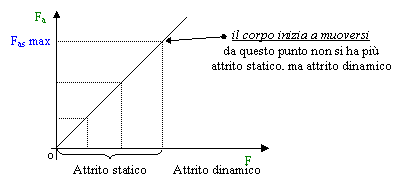
Il valore "Fas max" (forza di attrito massimo) dipende da due componenti:
la forza (N = Pn) che il corpo esercita sul piano di scorrimento;
il "coefficiente di attrito statico" (ms): un parametro che dipende dalle caratteristiche delle superfici che vengono a contatto.
![]() Quindi: Fas max
= ms N ; (possiamo anche dire che in ogni momento si ha Fas
ms N).
Quindi: Fas max
= ms N ; (possiamo anche dire che in ogni momento si ha Fas
ms N).
![]()
La direzione del vettore Fas è sempre uguale (ma di verso opposto) a quella della forza che causa il movimento del corpo al quale Fas si oppone.
Attrito dinamico di strisciamento
A differenza della forza di attrito statico, la forza di attrito dinamico è costante.
![]()
Si ha: Fad = md N (dove md indica il "coefficiente di attrito dinamico" e N = Pn).
Misura del coefficiente di attrito statico
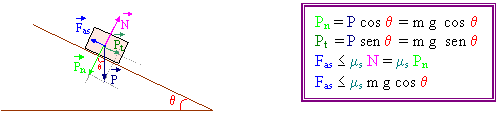
Fino a quando l'oggetto non si muove significa che c'è "equilibrio di forze" nelle due direzioni:
![]()
![]() "ortogonale" al piano: Pn
+ N = 0
"ortogonale" al piano: Pn
+ N = 0
![]()
![]() "parallela" al piano: Pt + Fas
= 0
"parallela" al piano: Pt + Fas
= 0
![]() Dalla seconda
relazione otteniamo che Fas max = Pt, ma si ha anche Fas max
= ms m g cos q, quindi: m g sen q ms m g cos q ms = tg q
Dalla seconda
relazione otteniamo che Fas max = Pt, ma si ha anche Fas max
= ms m g cos q, quindi: m g sen q ms m g cos q ms = tg q
Il "coefficiente di attrito" è determinato dal rapporto fra due forze, quindi risulta adimensionale.
Altri tipi di attrito
Oltre al tipo di attrito fin qui esaminato, ne esistono altri due tipi:
attrito volvente attrito causato da un corpo che "rotola" (per esempio una ruota che gira). Il suo valore è generalmente molto basso.
attrito viscoso attrito esercitato da un fluido (un gas o un liquido) su un corpo che si muove all'interno di esso. La direzione della forza di attrito è opposta a quella del vettore v che indica la velocità di movimento del corpo.
![]() Si ha: Fav =
k h v
Si ha: Fav =
k h v
k = coefficiente geometrico ("cx" dipende dalla forma dell'oggetto)
h = viscosità del fluido (dipende dalle caratteristiche del fluido stesso)
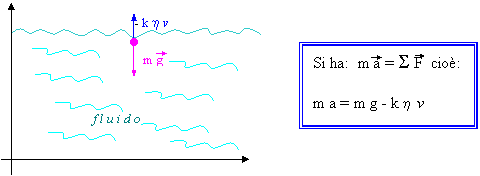 Esaminiamo il caso
di un corpo in caduta libera in un fluido
Esaminiamo il caso
di un corpo in caduta libera in un fluido
Consideriamo la velocità iniziale uguale a zero: l'attrito, di conseguenza, sarà nullo. All'aumentare della velocità si avrà un progressivo aumentare dell'attrito viscoso. Ad un certo punto però la forza di attrito viscoso controbilancerà esattamente la forza peso.
A questo punto (cioè quando mg - khv = 0) l'accelerazione diventa nulla e la velocità resta costante.
![]() A causa della
presenza dell'attrito viscoso, quindi, un corpo in caduta libera non può
acquistare una velocità superiore ad una certa velocità limite (dipendente dal
coefficiente geometrico del corpo e dal coefficiente di attrito viscoso del
fluido):
A causa della
presenza dell'attrito viscoso, quindi, un corpo in caduta libera non può
acquistare una velocità superiore ad una certa velocità limite (dipendente dal
coefficiente geometrico del corpo e dal coefficiente di attrito viscoso del
fluido): ![]() .
.
Lezione 8 (18 ottobre 1999)
Tipi di forze in Natura
In Natura esistono solo quattro tipi di forze:
Forze gravitazionali (si esercitano fra le masse: agiscono a livello macroscopico);
Forze elettromagnetiche (si esercitano fra le cariche: agiscono fra le molecole; mantengono unito l'atomo e sono responsabili delle "forze di attrito");
Forze deboli (o interazioni nucleari deboli: si trovano nei "decadimenti radioattivi");
Forze nucleari (si esercitano all'interno del nucleo atomico).
L'ordine di grandezza dell'intensità di queste forze è notevolmente diverso. Se poniamo idealmente l'intensità delle forze nucleari pari a "1", avremo che l'intensità delle forze deboli e dell'ordine di 10-7, quella delle forze elettromagnetiche è dell'ordine di 10-2 e quella delle forze gravitazionali è dell'ordine di 10-38. L'intensità di queste forze, però, varia notevolmente in base alla distanza che divide i "corpi" sui quali agisce: l'intensità della forza gravitazionale, ad esempio, è inversamente proporzionale al quadrato della distanza, mentre le forze nucleari sono molto forti solo per particelle particolarmente vicine, ma decrescono molto rapidamente all'aumentare della distanza.
Nota: In realtà due oggetti non si "toccano" mai, infatti, quando la distanza fra di essi è sufficientemente piccola, entrano in azione le forze elettromagnetiche: le cariche di segno opposto di attirano e quelle dello stesso segno si respingono. I contatti fra due corpi (a livello macroscopico) sono solo "apparenti".
Il concetto di "campo"
Per spiegare come avvenga l'interazione fra due oggetti sottoposte alle varie forze, nell'Ottocento Faraday introdusse il concetto di "campo".
Ogni oggetto genera intorno a sé un campo (gravitazionale, elettrico, ecc.) che esiste in maniera del tutto indipendente rispetto alla presenza di altri oggetti e che si estende all'infinito.
Per esempio: il Sole, possedendo una massa "M" genera intorno a sé un "campo gravitazionale" che esiste comunque indipendentemente dalla presenza della Terra o di altri corpi celesti. Se inseriamo la Terra all'interno del campo gravitazionale generato dal Sole vediamo che su di essa viene esercitata una forza F che "attira" la Terra verso il Sole.
Una situazione analoga si ha per le forze elettromagnetiche che generano un "campo elettrico".

LAVORO DI UNA FORZA
Consideriamo un oggetto puntiforme di massa "m" che si muova sotto l'azione di una forza (il concetto di "lavoro" è sempre legato a uno spostamento).

Osservazione:
Tenendo conto delle proprietà del prodotto scalare di due vettori possiamo affermare che:
![]()
![]()
![]()
![]()
![]()
![]() dW assume il massimo
valore positivo se F e ds
sono paralleli e hanno lo stesso verso;
dW assume il massimo
valore positivo se F e ds
sono paralleli e hanno lo stesso verso;
dW assume il massimo valore negativo se F e ds sono paralleli, ma hanno verso opposto;
dW assume valore nullo se F e ds sono ortogonali (ad esempio forza peso che agisce su un oggetto che si sposta su un piano orizzontale).
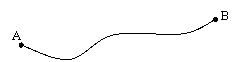 Se consideriamo un
punto che si muove lungo una traiettoria finita (da un punto A ad un punto B)
possiamo definire il "lavoro finito" W svolto dalla forza F:
Se consideriamo un
punto che si muove lungo una traiettoria finita (da un punto A ad un punto B)
possiamo definire il "lavoro finito" W svolto dalla forza F:
![]()
ENERGIA CINETICA
Quando un corpo si muove con velocità v questo ha un'energia
cinetica (o di movimento) che è pari a: ![]() (grandezza scalare
sempre positiva che si misura in "joule").
(grandezza scalare
sempre positiva che si misura in "joule").
Teorema dell'energica cinetica
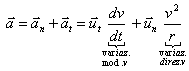
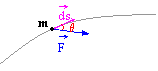
![]()
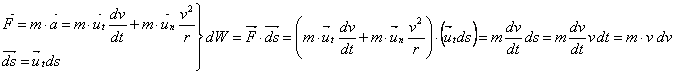
(solo la componente tangenziale della forza compie lavoro, la componente normale NO).
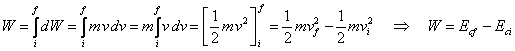
Il lavoro compiuto da una forza è uguale alla differenza fra l'energia cinetica finale e quella iniziale.
L'energia cinetica varia tutte le volte che varia il "modulo" della velocità (se si cambia solo la direzione della velocità non si hanno variazioni di energica cinetica).
Questo teorema vale per "qualsiasi tipo di forza". Nella dimostrazione abbiamo applicato solo l'ipotesi che la massa fosse costante (e questo è sempre vero nella "dinamica classica"), non abbiamo fatto alcuna ipotesi sulla natura della forza, quindi possiamo dire che vale per ogni F.
Forze conservative
Una forza è conservativa se il lavoro da essa svolto dipende SOLO dai punti "iniziale" e "finale" dello spostamento e NON dalla traiettoria seguita (es. forza peso, forze elastiche, ecc.).
Dimostriamo che la "forza peso" è una forza conservativa
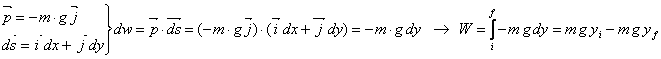
Il lavoro effettuato dipende solo dalla coordinata "y" del punto iniziale e del punto finale, non dalla traiettoria percorsa, quindi possiamo affermare che la forza pesò è una forza conservativa.
ENERGIA POTENZIALE (o energia di posizione)
L'energia potenziale di un punto materiale dipende dalla sua "posizione" ed è "associata" alla presenza di una "forza conservativa". Anche questa si misura in Joule.
In presenza di una "forza conservativa" possiamo dire che: W = Epi - Epf.
Ad esempio, nel caso precedentemente considerato, della forza peso si ha Ep = m g y + c
"c" è una costante che dipende dal valore di riferimento rispetto al quale calcoliamo l'altezza y (il suo valore è praticamente ininfluente in quanto lavorando su "differenze" di energia potenziale e non su valori assoluti la costante viene "eliminata" e non influisce sul risultato finale).
Teorema di conservazione dell'energia totale meccanica (vale solo per le forze conservative)
Quando sul moto di un corpo agiscono SOLO forze conservative si ha:
![]()
![]()
Se definiamo l'energia totale meccanica come: E = Ec + Ep , possiamo affermare che, durante un moto sotto l'azione di forze conservative, l'energia totale meccanica si mantiene costante.
Possiamo anche dire che: ![]() .
.
Si ha uno trasformazione di "forme di energia": ciò che viene perso come energia cinetica viene acquistato come energia potenziale e viceversa.
Lezione 9 (19 ottobre 1999)
Abbiamo dimostrato che la forza peso è una forza costante.
Sappiamo anche che la forza
peso: ![]() è una forza costante
in modulo, direzione e verso (nell'ipotesi di essere sufficientemente vicino
alla superficie terrestre da poter tralasciare la curvatura della Terra e la
variazione di g in base alla distanza dal centro della Terra).
è una forza costante
in modulo, direzione e verso (nell'ipotesi di essere sufficientemente vicino
alla superficie terrestre da poter tralasciare la curvatura della Terra e la
variazione di g in base alla distanza dal centro della Terra).
È possibile estendere la dimostrazione effettuata per la forza peso a tutte le forze costanti (prendendo un sistema di riferimento diretto secondo la direzione della forza stessa) e affermare che: le forze "costanti" sono tutte "conservative".
Quindi, in presenza di forze costanti, vale il "principio di conservazione dell'energia meccanica".
 Macchina di Atwood
Macchina di Atwood
 Proviamo a calcolare
la velocità delle due masse (si noti che è la stessa per entrambe) quando la
massa m2 è scesa di Dh (quindi,
analogamente, la massa m1 sarà salita di Dh).
Proviamo a calcolare
la velocità delle due masse (si noti che è la stessa per entrambe) quando la
massa m2 è scesa di Dh (quindi,
analogamente, la massa m1 sarà salita di Dh).
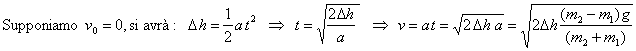
Lo stesso risultato si potrebbe ottenere effettuando delle "considerazioni energetiche", cioè applicando il principio di conservazione dell'energia meccanica (si noti che è possibile in quanto nel sistema agisce solo la forza peso che è una forza conservativa).
Si tenga conto che le considerazioni energetiche devono essere fatte sul "sistema" nella sua totalità e non sulle singole masse.

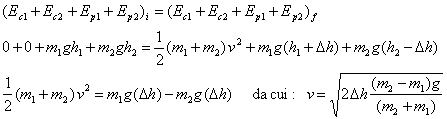
Pendolo semplice
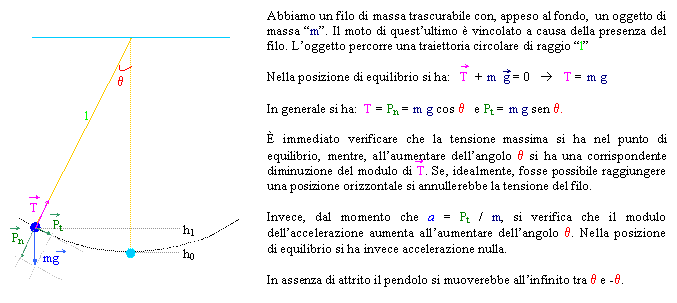
Conservazione dell'energia
In qualunque punto del movimento del pendolo (trascurando la presenza delle forze di attrito) si ha:
![]()
In assenza di forze dissipative il pendolo compie delle "oscillazioni persistenti" intorno alla propria posizione di equilibrio.
Se fossero presenti delle forze dissipative si avrebbero invece delle "oscillazioni smorzate".
Piccole oscillazioni
Quando l'angolo q è abbastanza piccolo (cioè sia tale che "sen q q") si può dimostrare che le oscillazioni compiute dal pendolo sono delle "oscillazioni armoniche".
![]()
a è l'accelerazione angolare; w è la pulsazione del pendolo; il segno - compare perché la forza che agisce sul pendolo è una "forza di richiamo" che tende a riportarlo nella posizione di equilibrio, quindi l'accelerazione ha sempre verso opposto a quella nella quale avviene il movimento).
Si ha anche ![]() cioè la pulsazione
del pendolo è determinata solo dal valore di g e dalla lunghezza del filo (non
dipende dalla massa attaccata al filo) e si ha:
cioè la pulsazione
del pendolo è determinata solo dal valore di g e dalla lunghezza del filo (non
dipende dalla massa attaccata al filo) e si ha: ![]() .
.
(Un pendolo lungo 1 m ha un periodo di oscillazione di circa 2 secondi).
Se gli angoli sono più grandi le oscillazioni sono sempre periodiche, ma non sono più armoniche.
Forze elastiche
Sono delle forze che "contrastano le deformazioni".
Quando si deforma un oggetto si creano al suo interno delle forze proporzionali alla deformazione stessa che, una volta eliminata la forza che l'aveva causata, tendono a eliminare la deformazione ritornando alla situazione iniziale (sempre che non sia stata superata la caratteristica di "elasticità" propria del corpo che è stato deformato).
![]() Un classico esempio
è quello di una "molla".
Un classico esempio
è quello di una "molla".

Si ha: F = - k x (k è detta "costante elastica" e dipende dal materiale con cui è costruita la molla)
Energia potenziale elastica
![]()
Il lavoro compiuto dipende solo dall'allungamento della molla: la forza elastica è una forza conservativa.
Definiamo "energia potenziale elastica": ![]() cost W = Epi - Epf = Ecf
- Eci.
cost W = Epi - Epf = Ecf
- Eci.
Vale il principio di conservazione dell'energia meccanica.
In una situazione fisica reale è possibile
che si debbano considerare contemporaneamente più energie potenziali diverse
(ad esempio nel caso di un oggetto "appeso" a una molla), in questo caso si può
affermare che: ![]() .
.
Lezione 10 (25 ottobre 1999)
![]()
![]() La relazione: Forza elastica F = - k x prende il nome di "legge di Hooke".
La relazione: Forza elastica F = - k x prende il nome di "legge di Hooke".
La costante elastica "k" si misura in N/m.
Quando si sposta un oggetto attaccato a una molla dalla sua "posizione di equilibrio" il sistema "molla + massa" acquista energia. Dal momento che vale il principio di conservazione dell'energia meccanica è evidente che questa "energia acquisita" deve essere fornita dall'esterno.
L'aumento di energia del sistema è uguale al "lavoro" compiuto dalle forze esterne.
Per effetto delle forze
esterne che comprimono o allungano la molla il sistema acquista una certa
"energia potenziale iniziale" pari a ![]() (in questo momento si
ha Ep = max e Ec
= 0).
(in questo momento si
ha Ep = max e Ec
= 0).
Quando si elimina l'azione delle forze esterne lasciando l'oggetto libero di muoversi quest'ultimo sarà soggetto all'azione di una "forza di richiamo" che tenderà a riportare l'oggetto nella posizione di equilibrio. Il sistema perderà gradualmente energia potenziale che si trasformerà in energia cinetica. Una volta raggiunta la posizione di equilibrio si avrà: Ep = 0 e Ec = max.
Il sistema continua comunque a muoversi nella stessa direzione ritrasformando gradualmente energia cinetica in energia potenziale fino a raggiungere la posizione "-x0" nella quale si avrà nuovamente Ep = max e Ec = 0.
È evidente che il sistema avrà velocità massima nel punto di equilibrio e nulla nei due punti estremi; per l'accelerazione invece si avrà un massimo nei due estremi e zero nel punto di equilibrio.
In assenza di forze di attrito il sistema oscilla indefinitamente tra la posizione x0 e la posizione -x0.
Si può dimostrare che si tratta di "oscillazioni armoniche".
![]()
dove la pulsazione w è uguale a ![]() , da cui si ottiene che il periodo T è uguale a
, da cui si ottiene che il periodo T è uguale a ![]() .
.
I valori xo e j che compaiono nell'equazione del moto armonico dipendono dalle condizioni iniziali del sistema. Il periodo di oscillazione invece dipende solo dalle caratteristiche del sistema (massa e costante elastica della molla), ma, come nel caso del pendolo, non dipende dall'allungamento x0.
Il tempo impiegato per compiere un'oscillazione completa (in assenza di attrito) è indipendente dall'ampiezza dell'oscillazione stessa (se l'oscillazione è più ampia risulterà maggiore la velocità).
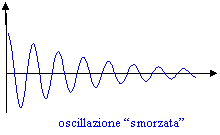
 Nella realtà la
presenza delle forze d'attrito genera delle "oscillazioni smorzate" fino a
fermare il sistema nella sua posizione di equilibrio (si ha:
Nella realtà la
presenza delle forze d'attrito genera delle "oscillazioni smorzate" fino a
fermare il sistema nella sua posizione di equilibrio (si ha: ![]() presenza di attrito viscoso).
presenza di attrito viscoso).
![]() .
.
La soluzione di questa equazione differenziale del secondo ordine corrisponde all'equazione del "moto armonico smorzato". Il fattore di smorzamento (che dipende dalla velocità e dalla massa dell'oggetto) causa l'introduzione nella soluzione di un esponenziale negativo.
Massa "appesa" a una molla
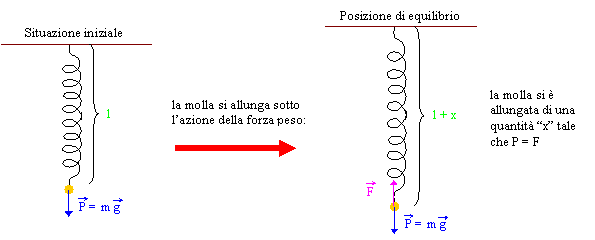 Per misurare le
forze spesso si usa un "dinamometro" il cui principio di funzionamento è basato
sulla "misura" dell'allungamento di una molla sotto l'azione di una forza.
Per misurare le
forze spesso si usa un "dinamometro" il cui principio di funzionamento è basato
sulla "misura" dell'allungamento di una molla sotto l'azione di una forza.
Si raggiunge la posizione di equilibrio
quando la forza peso è bilanciata esattamente dalla forza elastica della molla,
quindi si avrà: ![]() .
.
Nella situazione iniziale si ha: Ecinetica = 0 - Epot.molla = 0 - Epot.peso = max.
Quando l'oggetto viene lasciato libero la molla si allunga verso il basso: si ha una perdita di energia potenziale della forza peso che si trasforma in energia cinetica e energia potenziale elastica.
Una volta raggiunta la posizione di equilibrio l'oggetto continuerà a muoversi trasformando l'energia cinetica acquistata in energia potenziale elastica raggiungendo una posizione simmetrica a quella iniziale rispetto al punto di equilibrio (allungamento totale: l + 2xeq).
In questo caso si ha un bilancio della "conservazione dell'energia" con due diverse energie potenziali (peso e elastica).
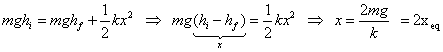 (x = allungamento
totale molla)
(x = allungamento
totale molla)
Interazione gravitazionale e "legge di gravitazione universale"
Prese due masse puntiformi poste a una certa
distanza "r" fra queste due masse si esercita una forza di tipo attrattivo
direttamente proporzionale al prodotto delle masse e inversamente proporzionale
al quadrato della distanza: ![]()
(G = costante di gravitazione universale = 6.67 10-11 N m2 / Kg2; la misura di questa costante è molto "delicata" in quanto bisogna supporre che le due masse interagiscano solo fra di loro, senza interferire con altre masse del mondo esterno).
Osservazione
Il concetto di "massa gravitazionale" è teoricamente diverso da quello di "massa inerziale".
Infatti la "massa gravitazionale" è la proprietà di un oggetto che fa sì che esso interagisca con altri oggetti attraendoli e venendo a sua volta attratto da essi.
La "massa inerziale" invece è l'inerzia che ha un corpo a cambiare il suo stato di quiete o di moto rettilineo e uniforme.
In realtà si può dimostrare che hanno lo stesso valore, si può quindi parlare genericamente di "massa" senza distinguere tra "inerziale" e "gravitazionale".
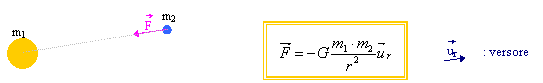 Supponiamo che una
delle due masse sia ferma (per esempio se è molto maggiore dell'altra oppure se
è fissata). Consideriamo solo la forza che agisce sulla massa in movimento.
Supponiamo che una
delle due masse sia ferma (per esempio se è molto maggiore dell'altra oppure se
è fissata). Consideriamo solo la forza che agisce sulla massa in movimento.
La Forza di gravità è una "forza centrale", ciò diretta sempre verso uno stesso punto che viene detto "centro di forza" (sarebbe centrale anche se avesse verso opposto).
Energia potenziale gravitazionale
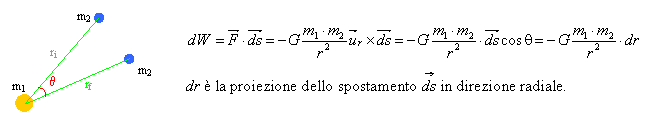 Dimostriamo che il
lavoro fatto dalla forza gravitazionale dipende solo dal punto iniziale e da
quello finale e non dal percorso compiuto.
Dimostriamo che il
lavoro fatto dalla forza gravitazionale dipende solo dal punto iniziale e da
quello finale e non dal percorso compiuto.
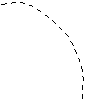
![]() : il lavoro svolto non dipende dalla traiettoria.
: il lavoro svolto non dipende dalla traiettoria.
Possiamo quindi definire l'energia potenziale
gravitazionale: ![]() e affermare che, come
nei casi precedenti si ha: W = Epi - Epf.
e affermare che, come
nei casi precedenti si ha: W = Epi - Epf.
La forza gravitazionale è una forza centrale. Si può dimostrare che tutte le forze centrali sono conservative (si può applicare il principio di conservazione dell'energia meccanica).
Nota: la forza peso (studiata in precedenza) è un caso particolare di "interazione gravitazionale".
Conoscendo il valore della massa e del raggio della Terra è possibile calcolare il valore di g.
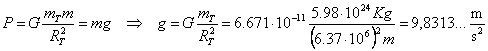 .
.
In realtà è abbastanza facile calcolare sperimentalmente il valore di g.
Questo procedimento è stato applicato in senso inverso per calcolare la massa della Terra.
Lezione 11 (26 ottobre 1999)
Relazione tra forza ed energia potenziale (nelle Forze Conservative).
![]() : il lavoro compiuto dipende solo dal punto iniziale e da
quello finale.
: il lavoro compiuto dipende solo dal punto iniziale e da
quello finale.
Energia di posizione: Ep = f (x, y, z) coordinate spaziali "cartesiane"
Ep = f (r, q j) coordinate spaziali "sferiche"
(r = raggio della terra, q = latitudine, j = longitudine)
Superfici equipotenziali
Una "superficie equipotenziale" è il luogo dei punti nei quali si ha Ep = costante.
La forma della superficie equipotenziale dipende ovviamente dall'equazione che esprime Ep.
Esempio: Forza peso Ep = m g y (solo funzione di y)
Le superfici equipotenziali sono dei piani paralleli alla superficie terrestre.
Forza
gravitazionale Ep = ![]() (solo funzione di r)
(solo funzione di r)
In questo caso è più pratico utilizzare le coordinate polari.
Le superfici equipotenziali sono delle superfici sferiche.
Si osserva anche che il vettore di una forza conservativa è diretto sempre ortogonalmente alla sua superficie equipotenziale e punta nel verso nel quale l'energia potenziale decresce.
Infatti se ci muoviamo lungo una superficie equipotenziale si ha Ep = costante e quindi W = 0.
Dal momento che ![]() si deve avere
necessariamente q = 90° (assumendo
che sia lo spostamento che la forza abbiano modulo diverso da zero).
si deve avere
necessariamente q = 90° (assumendo
che sia lo spostamento che la forza abbiano modulo diverso da zero).
Conoscendo la formula che esprime l'energia potenziale è possibile ricavare il vettore della corrispondente forza conservativa F.
Infatti visto che: ![]() possiamo dire che la
quantità
possiamo dire che la
quantità ![]() è il "differenziale esatto"
della funzione Ep cambiato di segno.
è il "differenziale esatto"
della funzione Ep cambiato di segno.
gradiente di Ep
![]() variazione della
funzione Ep al variare di x, y e z (di dx, dy e dz).
variazione della
funzione Ep al variare di x, y e z (di dx, dy e dz).
![]()
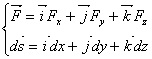
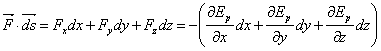
da cui si ha: ![]() .
.
Nota: Ep è una grandezza scalare, mentre il "gradiente di Ep" è una grandezza vettoriale.
Si ha un gradiente ogni volta che si ha una "variazione" nella grandezza considerata.
Dal momento che F = - grad (Ep) si può dire che il gradiente è sempre ortogonale alla superficie equipotenziale e punta nel verso nel quale l'energia potenziale aumenta.
Punti di Equilibrio (grafici dell'energia potenziale)
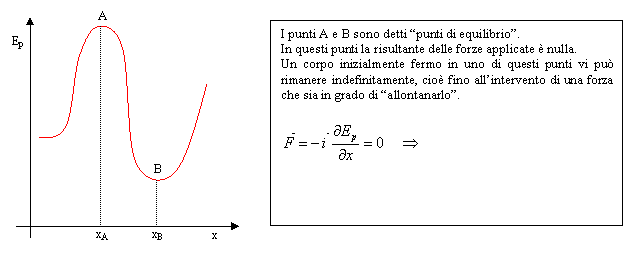 Disegniamo una
ipotetica curva che rappresenti un energia potenziale funzione della sola x:
Disegniamo una
ipotetica curva che rappresenti un energia potenziale funzione della sola x:
un punto di
equilibrio è un punto nel quale la derivata parziale si annulla, è quindi
un punto di "massimo" oppure di "minimo".
Il punto A è un "punto di equilibrio instabile": non appena un corpo inizialmente fermo in A si sposti, per una causa qualsiasi, in una delle due direzioni le forze legate all'energia potenziale tenderanno ad allontanarlo definitivamente dal punto di equilibrio.
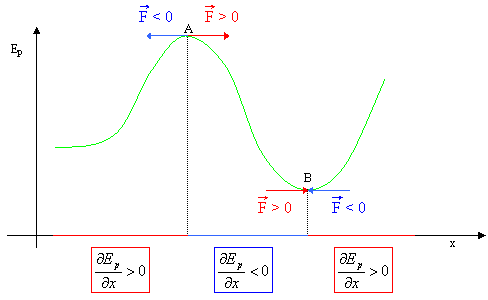 Il punto B è un "punto di equilibrio stabile": non appena un corpo
inizialmente fermo in B si sposti, per una causa qualsiasi, in una delle due
direzioni le forze legate all'energia potenziale tenderanno a riportarlo nella
posizione di equilibrio stabile.
Il punto B è un "punto di equilibrio stabile": non appena un corpo
inizialmente fermo in B si sposti, per una causa qualsiasi, in una delle due
direzioni le forze legate all'energia potenziale tenderanno a riportarlo nella
posizione di equilibrio stabile.
Lavoro su una linea chiusa (circuitazione di F)
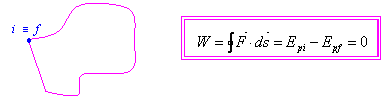 Una forza
conservativa compie un lavoro nullo agendo lunga una linea chiusa.
Una forza
conservativa compie un lavoro nullo agendo lunga una linea chiusa.
In generale, quando si parla di "circuitazione", non è detto che ci si riferisca ad un "lavoro".
![]() Si ha la "circuitazione di un vettore" quando si calcola
l'integrale lungo una curva chiusa del prodotto scalare del vettore stesso per
il vettore ds.
Si ha la "circuitazione di un vettore" quando si calcola
l'integrale lungo una curva chiusa del prodotto scalare del vettore stesso per
il vettore ds.
Il vettore potrebbe non essere una forza, ma un vettore qualsiasi. In questo caso quindi non si parla più di "forze conservative", ma di "campo conservativo".
FORZE NON CONSERVATIVE (Le Forze di Attrito)
Dimostriamo che le forze d'attrito non sono conservative, cioè che il lavoro da esse svolto "dipende" dalla traiettoria percorsa.
Nota: Le forze di attrito hanno sempre la stessa direzione del movimento, ma con verso opposto; quindi l'angolo compreso tra i vettori "forza" e "spostamento" sarà di 180° (p radianti).
![]()
(S1 rappresenta la "lunghezza del percorso" compiuto tra i e f; abbiamo anche supposto, per semplicità di calcolo, che la forza fosse costante, ma questa ipotesi non è necessaria).
Abbiamo dimostrato che il lavoro svolto dalle forze di attrito è uguale alla "forza" esercitata per la "lunghezza del percorso". Quindi se si cambia il percorso anche il lavoro compiuto cambia.
![]() In presenza di forze
non conservative NON si può applicare il principio di conservazione
dell'energia meccanica, è comunque valido il teorema dell'energia cinetica.
In presenza di forze
non conservative NON si può applicare il principio di conservazione
dell'energia meccanica, è comunque valido il teorema dell'energia cinetica.
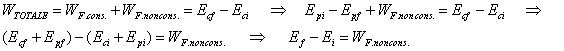
![]() Non si ha più
conservazione dell'energia meccanica.
Non si ha più
conservazione dell'energia meccanica.
Dal momento che le forze di attrito producono sempre un lavoro negativo si avrà Ef < Ei (l'attrito fa perdere energia meccanica). Globalmente comunque l'energia si conserva. La parte di energia meccanica "persa" a causa dell'attrito si trasforma in altre forme di energia (es. energia termica).
IMPULSO DI UNA FORZA
 In generale le forze
applicate non sono costanti, ma variano in funzione del tempo.
In generale le forze
applicate non sono costanti, ma variano in funzione del tempo.
Osservazione: per ottenere la stessa variazione di quantità di moto non è necessario applicare sempre una stessa forza, è sufficiente che le due forze applicate abbiano lo "stesso impulso" (cioè che l'area sottesa alla curva che rappresenta la variazione della forza rispetto al tempo sia la stessa).
Forze impulsive
Sono forze molto intense che agiscono per un tempo molto breve (ad esempio nel caso degli urti).
 Momento della quantità di moto (o momento
angolare)
Momento della quantità di moto (o momento
angolare)
Momento della forza

Relazione fra "momento angolare" e "momento della forza"
![]()
![]()
![]()
Conservazione del momento angolare
![]()
Vogliamo scoprire quando si "conserva" il momento angolare, cioè in quali condizioni L è costante.
![]()
![]()
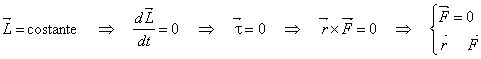
Il momento angolare si conserva se non c'è nessun momento di forza, quindi se la risultante delle forze applicate è nulla oppure è applicata parallelamente al vettore posizione (ad esempio nel caso di una forza centrale quando l'origine è nel centro di forza).
Lezione 12 (2 novembre 1999)
Sistemi di particelle
Sistema discreto: sistema costituito da un certo numero di "particelle puntiformi".
Sistema continuo: corpo rigido (lo trattiamo in modo analogo al caso precedente immaginando di dividerlo in tanti elementini di massa dm ognuno dei quali sia abbastanza piccolo da poter essere considerato puntiforme).
Centro di massa: punto ideale di un corpo nel quale (almeno per certi tipi di problemi) si può pensare che sia "concentrata" tutta la massa del corpo (coincide con il "centro di gravità").
Ad esempio un corpo sferico di densità uniforme avrà il centro di massa nel centro della sfera.
Centro di massa di un sistema di particelle
immaginiamo di avere due corpi di massa "m" posti
sull'asse x rispettivamente nel punto x1 e nel punto x2,
allora possiamo dire che: ![]() (media aritmetica);
(media aritmetica);
se invece i due corpi avessero massa diverse
(rispettivamente m1 e m2) il centro di massa risulterebbe
"spostato" verso la massa più grande: ![]() (media ponderata);
(media ponderata);

![]() estendendo quanto
sopra a un generico sistema formato da "n" particelle e lavorando in tre
dimensioni si ha:
estendendo quanto
sopra a un generico sistema formato da "n" particelle e lavorando in tre
dimensioni si ha:  (dove con ri intendiamo il vettore
posizione della i-esima particella e con M
la massa totale del sistema).
(dove con ri intendiamo il vettore
posizione della i-esima particella e con M
la massa totale del sistema).
Centro di massa di un corpo rigido
 Operiamo in modo
analogo al caso di "n" particelle. Supponiamo di dividere il corpo in tante
masse dm tanto piccole da poter
essere considerate puntiformi e poi integriamo:
Operiamo in modo
analogo al caso di "n" particelle. Supponiamo di dividere il corpo in tante
masse dm tanto piccole da poter
essere considerate puntiformi e poi integriamo: 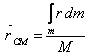 .
.
In realtà il calcolo non viene effettuato
sulla massa, ma sul volume applicando la relazione ![]() (dove r rappresenta la "densità"
del corpo, che può essere o meno uniforme).
(dove r rappresenta la "densità"
del corpo, che può essere o meno uniforme).
Dinamica di un sistema di particelle
In un sistema di particelle possiamo distinguere due tipi di forze:
forze interne: dovuta all'interazione delle particelle fra di loro; si ha sempre un'interazione tra "coppie" di particelle e, in base al principio di "azione e reazione", si può affermare che la sommatoria di tutte le forze interne risulta uguale a zero;
forze esterne: dovute a "eventuali" interazioni delle particelle con l'ambiente esterno.
Un sistema che non interagisce con l'esterno viene detto SISTEMA ISOLATO.
 Quantità di moto di
un sistema di particelle
Quantità di moto di
un sistema di particelle
Quantità di moto "totale" del sistema: ![]() .
.
Ricordiamo che, in base alla II legge della
dinamica, si ha: ![]() .
.
Ricaviamo la variazione della quantità di moto delle singole particelle del sistema:
![]()
![]()
Per quanto riguarda la quantità di moto "totale" del sistema invece si ha:
![]()
![]()
![]() .
.
In un sistema isolato (nel quale la
sommatoria delle forze esterne è nulla) si avrà: ![]() , cioè
, cioè ![]() costante: "la quantità di moto totale di un sistema isolato si
conserva".
costante: "la quantità di moto totale di un sistema isolato si
conserva".
Moto del "centro di massa"
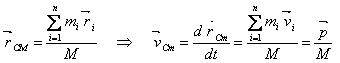 il centro di massa
si comporta come un "punto materiale" che trasporta tutta la quantità di moto
del sistema.
il centro di massa
si comporta come un "punto materiale" che trasporta tutta la quantità di moto
del sistema.
In un sistema isolato la quantità di moto è costante, quindi anche la velocità del centro di massa risulta costante: "in un sistema isolato il centro di massa si muove di moto rettilineo uniforme".
![]() : "sul centro di massa agisce la
risultante di tutte le forze esterne"
: "sul centro di massa agisce la
risultante di tutte le forze esterne"
Le forze interne non influiscono in alcun modo sul moto del centro di massa. Sono responsabili solo del moto delle particelle all'interno del sistema.
Esempio: una cassa di esplosivo che viaggia con moto rettilineo uniforme esplode sotto l'azione delle forze interne dividendosi in tanti frammenti. Risulta molto complicato studiare il moto dei singoli frammenti. Possiamo però affermare che il centro di massa dei frammenti continua a muoversi di moto rettilineo uniforme alla stessa velocità che aveva prima di esplodere.
Esempio: un missile lanciato in aria viaggia secondo la classica traiettoria parabolica del "moto del proiettile". A un certo punto esplode in tanti frammenti sotto l'azione delle forze interne. Possiamo comunque affermare che il centro di massa dei frammenti continuerà a muoversi secondo la traiettoria parabolica originariamente seguita dal missile. I frammenti invece si muoveranno in traiettorie diverse sotto l'azione delle forze interne.
Energia cinetica di un sistema di particelle
L'energia cinetica totale di un sistema di
"n" particelle è data dalla somma delle energie cinetiche di tutte le singole
particelle: ![]() .
.
Il "teorema dell'energia cinetica", essendo
valido per ogni singola particella, vale anche per un sistema di particelle in
generale: ![]() .
.
Se le forze interne sono "conservative" si
può scrivere: ![]() da cui possiamo
ricavare la seguente relazione:
da cui possiamo
ricavare la seguente relazione: ![]() .
.
La quantità: Ec + Ep int. prende il nome di "energia interna" (o propria) di un sistema.
In un sistema isolato l'energia interna si conserva (si possono comunque avere trasformazioni di Ec in Ep e viceversa nelle singole particelle).
URTI
 Quando due
particelle si urtano si ha l'azione di forze interne di tipo "impulsivo".
Quando due
particelle si urtano si ha l'azione di forze interne di tipo "impulsivo".
Per quanto riguarda il momento dell'urto il sistema formato dalle due particelle che si scontrano può essere considerato "isolato". Infatti, nel momento nel quale si scontrano, la forza dell'urto è molto maggiore rispetto a tutte le altre forze eventualmente coinvolte. Possiamo quindi compiere un'approssimazione e considerarla come se fosse l'unica.
Il vantaggio nel considerare il sistema come se fosse isolato consiste nella possibilità di applicare il "principio di conservazione della quantità di moto".
Applicando il suddetto principio si ha: ![]()
Questo principio è valido in ogni tipo di urto.
Esistono due diversi tipi di urti: "urti elastici" e "urti anelastici".
Urti elastici
Si ha un urto "perfettamente elastico" quando due oggetti si urtano senza deformarsi.
In natura non è possibile generare un urto perfettamente elastico; ci sono però alcune situazioni che si possono approssimare a un urto elastico (es. lo scontro di due palline di acciaio, l'urto fra due palle da biliardo, ecc.).
In un urto "perfettamente elastico" si conserva l'energia cinetica del sistema (trascuriamo le perdite di energia dovute all'attrito, alle onde sonore, ecc.).
Non si hanno perdite di energia dovute alla deformazione dei corpi (quando un corpo si deforma, infatti si ha una variazione delle energie potenziali delle particelle presenti all'interno del corpo; quindi una parte dell'energia cinetica del sistema si trasforma in energia potenziale).
Nello studio di un urto elastico possiamo quindi utilizzare due equazioni:
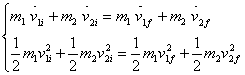
Urti anelastici
Si ha un urto "anelastico" quando due oggetti urtandosi si deformano.
Gli urti anelastici possono essere di due tipi:
urti "endotermici" sono urti nei quali si perde Ec e si acquista Ep (sono i più frequenti)
urti "esotermici" sono urti nei quali si acquista Ec e si perde Ep (poco frequenti)
Un urto si dice "perfettamente anelastico" se i due oggetti, dopo lo scontro, restano "uniti".
Urti unidimensionali
Si ha un urto "unidimensionale" quando le particelle, prima e dopo l'urto, si muovono lunga una stessa direzione fissa (ad esempio l'asse x).
Nel caso di un urto elastico unidimensionale, risolvendo le due equazioni trovate, si ottiene:
![]()
Casi particolari
m1 = m2 (masse uguali) v1f = v2i e v2f = v1i (i due corpi si scambiano le velocità)
(se la particella 2 fosse inizialmente ferma si avrebbe v1f = 0 e v2f = v1i)
m2 >> m1 (bersaglio di grande massa fermo) v1f - v1i e v2f
(la particella 1 rimbalza indietro con la stessa velocità, mentre il bersaglio resta fermo)
m2 << m1 (bersaglio di massa piccola fermo) v1f v1i e v2f 2 v1i
(la particella 1 prosegue circa con la stessa velocità e la particella 2 acquista velocità doppia)
Lezione 13 (3 novembre 1999)
Urto completamente anelastico
In questo caso si conserva la quantità di moto, ma non l'energia cinetica del sistema.
L'equazione della conservazione
della quantità di moto diventa: ![]() .
.
Infatti i due corpi, dal
momento che dopo l'urto rimangono attaccati, avranno la stessa velocità finale
che sarà uguale a ![]() .
.
Osservazione: il centro di massa continua a muoversi di
moto rettilineo uniforme. La sua velocità prima dell'urto era infatti ![]() (velocità finale dei
due corpi rimasti uniti e quindi anche del loro centro di massa). Durante
l'urto infatti agiscono solo "forze interne" che non influiscono sul moto del
centro di massa.
(velocità finale dei
due corpi rimasti uniti e quindi anche del loro centro di massa). Durante
l'urto infatti agiscono solo "forze interne" che non influiscono sul moto del
centro di massa.
Potremmo anche studiare l'urto in un sistema di riferimento solidale con il centro di massa. In questo caso la quantità di moto sarebbe uguale a zero e le due masse si muoverebbero sempre in direzioni opposte (avvicinandosi o allontanandosi).
Urti elastici bidimensionali (ad esempio l'urto di due palle da biliardo)
Si applicano sempre le due condizioni di "conservazione della quantità di moto" e "conservazione dell'energia cinetica", ma in questo caso bisogna tenere conto delle componenti della velocità.
Se lavoriamo nel piano xy otteniamo tre equazioni:

In generale però ci sono quattro incognite (i moduli delle due velocità finali e le loro direzioni). È molto difficile "calcolare" i due angoli in base alle forze che agiscono nell'urto. Normalmente è più comodo "misurare" uno dei due angoli e ricavare le altre incognite tramite le equazioni suddette.
Lezione 14 (8 novembre 1999)
Dinamica del corpo rigido
Corpo rigido: oggetto solido che supponiamo assolutamente "indeformabile" (le distanze fra le particelle al suo interno sono costanti).
Traslazione
Si ha un moto di "pura traslazione" quando tutti i punti del corpo si muovono su traiettorie parallele. In questo caso per studiare il moto del corpo rigido è sufficiente studiare il moto del centro di massa (che è rappresentativo del moto dell'intero corpo).
Un corpo si muove in questo modo se la "forza" che causa il movimento viene applicata nel centro di massa (in caso contrario si avrà anche un moto "rotazionale").
Rotazione
Si ha un moto di "pura rotazione" quando tutti i punti del corpo descrivono traiettorie circolari intorno ad un asse che viene detto "asse di rotazione". In generale l'asse di rotazione non coincide con il centro di massa, ma può dipendere da eventuali vincoli esterni).
 In generale un corpo
rigido descriverà un moto "roto-traslatorio" che può essere studiato
dividendolo in due moti distinti: una "traslazione" del centro di massa e una
"rotazione" intorno ad un asse passante per il centro di massa (se ne ha un
esempio nel moto della ruota di un automobile).
In generale un corpo
rigido descriverà un moto "roto-traslatorio" che può essere studiato
dividendolo in due moti distinti: una "traslazione" del centro di massa e una
"rotazione" intorno ad un asse passante per il centro di massa (se ne ha un
esempio nel moto della ruota di un automobile).

Energia cinetica di rotazione
![]()
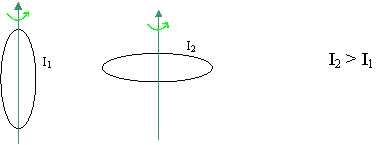 I è il "momento d'inerzia" del corpo; il suo valore
dipende dalla "struttura" del corpo e dalla scelta dell'asse di rotazione. Si
misura in Kg m2. Si può considerare come l'equivalente rotazionale
della "massa" di un corpo (cioè la sua inerzia a porsi in rotazione intorno ad
un certo asse).
I è il "momento d'inerzia" del corpo; il suo valore
dipende dalla "struttura" del corpo e dalla scelta dell'asse di rotazione. Si
misura in Kg m2. Si può considerare come l'equivalente rotazionale
della "massa" di un corpo (cioè la sua inerzia a porsi in rotazione intorno ad
un certo asse).
Lavoro in un moto rotazionale
 Nota: Si definisce
"potenza" la quantità di lavoro compiuta per unità di tempo; si misura in Watt.
Nota: Si definisce
"potenza" la quantità di lavoro compiuta per unità di tempo; si misura in Watt.
(Watt = Joule/s) ![]() supponendo F
costante rispetto a t.
supponendo F
costante rispetto a t.
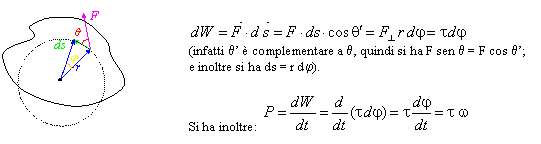 Osservazione: Anche se il modulo della
forza applicata è diverso da zero non è detto che si abbia un "momento di
forza" non nullo. Si ha un momento di forza uguale a zero se:
Osservazione: Anche se il modulo della
forza applicata è diverso da zero non è detto che si abbia un "momento di
forza" non nullo. Si ha un momento di forza uguale a zero se:
non si applica alcuna forza (oppure la risultante delle forze applicate è nulla);
si applica la forza nell'asse di rotazione (in questo caso si ha r = 0);
si applica una forza parallelamente all'asse di rotazione (si ha cioè sen q = 0), in questo caso non si ha una rotazione, ma, se il corpo non è vincolato, si potrebbe avere una traslazione.
![]() (nell'ipotesi che t sia costante).
(nell'ipotesi che t sia costante).
Per il teorema dell'energia cinetica si
ha: ![]() .
.
Il lavoro fatto dalla forza si trasforma in energia cinetica rotazionale.
 Momento della
quantità di moto di un corpo rigido che ruota
Momento della
quantità di moto di un corpo rigido che ruota
Per trovare il momento della quantità di moto totale di un corpo bisogna sommare i momenti delle quantità di moto di tutti i singoli elementini dm.
Se l'asse di rotazione coincide con un asse di simmetria le varie componenti ortogonali all'asse si annullano per motivi di simmetria e rimane solo la componente parallela all'asse di rotazione.
(In effetti in ogni corpo esistono tre particolari assi detti "assi principali d'inerzia" per i quali vale quanto appena detto per gli assi di simmetria.)
![]()
![]()
Se la rotazione avviene lungo uno degli assi
principali d'inerzia, si può dire anche che: ![]()
(Per semplicità noi ci riferiremo sempre a situazioni di questo tipo).
Lezione 15 (9 novembre 1999)
Relazione tra "momento angolare" e "momento della forza" nel corpo rigido
![]()
Si può dimostrare che le forze interne non
hanno momento e quindi che ![]() .
.
![]()
(legge della dinamica del corpo rigido equivalente alla seconda legge della dinamica: F = m a).
|
Schema riassuntivo |
|
|
Dinamica del punto |
Dinamica del corpo rigido |
|
|
|
|
|
|
|
|
|
|
|
|
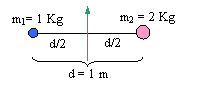 Esempi di calcolo
del momento d'inerzia:
Esempi di calcolo
del momento d'inerzia: ![]()
1. ![]()
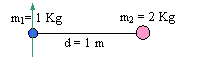
2. ![]()
![]()
![]()
![]() 3. I molto piccolo I
3. I molto piccolo I
4. Corpo continuo: ![]() (questo integrale è
abbastanza facile da calcolare per i corpi geometrici "noti" quali sfera,
cilindro, ecc.; può essere molto difficile per corpi irregolari).
(questo integrale è
abbastanza facile da calcolare per i corpi geometrici "noti" quali sfera,
cilindro, ecc.; può essere molto difficile per corpi irregolari).
Conservazione del momento angolare di un corpo rigido
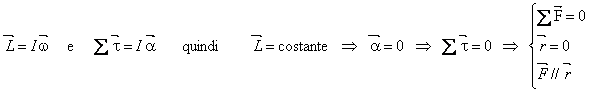
Quindi se 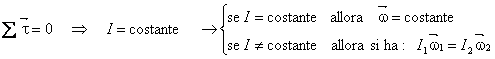
Se ne ha un esempio nel caso del pattinatore che ruota (verticalmente) su sé stesso più o meno velocemente (a parità di altre condizioni) a seconda che abbia le braccia aperte oppure chiuse.
Chiudendo le braccia infatti diminuisce il suo momento d'inerzia aumentando di conseguenza la sua velocità angolare. Quanto detto è vero in quanto non c'è alcun momento di forze esterne. La chiusura delle braccia è causata da "forze interne" che non influiscono sul momento angolare.
Osservazione: la conservazione del momento angolare è completamente indipendente rispetto alla conservazione dell'energia cinetica. Nel caso del pattinatore, per esempio, si ha un aumento di energia cinetica dovuto al lavoro fatto dalle forze interne.
Osservazione: se l'asse di rotazione non è perfettamente verticale, ma è inclinato (come nel caso della trottola) si ha un "moto di precessione". Mentre la trottola gira su stessa si ha un contemporaneo moto "conico" dell'asse. In questo caso il momento delle forze esterne non è nullo in quanto agisce una componente della forza peso.
Coppia di forze
Si ha una coppia di forze quando ci sono due forze uguali in modulo e direzione, ma di verso opposto. Applicate a un corpo rigido causano solo una rotazione e non una traslazione.
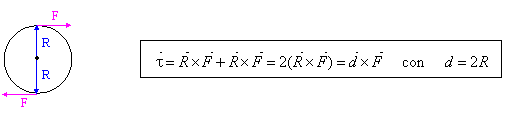
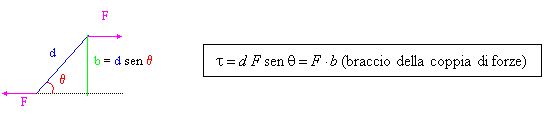 In generale si ha:
In generale si ha:
Lezione 16 (10 novembre 1999)
PROPAGAZIONE PER ONDE
Abbiamo due tipi di onde: "onde meccaniche" e "onde non meccaniche".
Le onde meccaniche sono onde che necessitano di un mezzo per propagarsi. Sono esempi di onde meccaniche le onde in una corda, le onde di pressione (onde sonore), le onde sull'acqua, ecc.
Le onde non meccaniche invece si propagano anche nel vuoto. Si tratta essenzialmente delle "onde elettromagnetiche" (onde radio, luce visibile, raggi x, ecc.).
Le onde meccaniche si originano a causa delle caratteristiche di elasticità del mezzo nel quale si propagano. Quando si sollecita un mezzo elastico si causa una "deformazione" in un certo punto che viene trasmessa ai punti vicini propagandosi lungo il mezzo considerato.
Anche i gas reagiscono in modo elastico alle deformazioni (si hanno zone di compressione e rarefazione che si propagano).
La corda di una chitarra che vibrasse nel vuoto non provocherebbe alcun effetto sul mondo esterno. Quando invece si è in presenza di aria la vibrazione della corda crea delle onde di compressione e di rarefazione nell'aria che, partendo dalla corda, si propagano in "tutte" le direzioni fino a raggiungere la membrana presente all'interno dell'orecchio che inizia a vibrare trasmettendo le informazioni ricevute al cervello che le percepisce come "suoni".
È evidente che, per le onde meccaniche, è fondamentale la presenza di un mezzo di propagazione.
Le onde possono poi suddividersi in due classi: "onde longitudinali" e "onde trasversali".
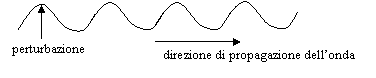 Nel caso delle onde
trasversali la direzione di propagazione dell'onda è ortogonale alla direzione
nella quale è avvenuta la perturbazione (ad esempio: le onde in una corda).
Nel caso delle onde
trasversali la direzione di propagazione dell'onda è ortogonale alla direzione
nella quale è avvenuta la perturbazione (ad esempio: le onde in una corda).
Nel caso delle onde longitudinali invece la direzione di propagazione dell'onda e la perturbazione hanno la stessa direzione (ad esempio: onde sonore).
Le onde elettromagnetiche sono onde trasversali.
Esistono anche "onde ibride" (ad esempio le onde generate da un sasso lanciato nell'acqua).
È fondamentale ricordare che le onde (di qualsiasi tipo esse siano) trasportano SOLO ENERGIA. Non si ha MAI un trasporto di MATERIA. La materia subisce solo dei piccoli movimenti locali.
Lezione 17 (15 novembre 1999)
Descrizione matematica di una propagazione per onde

 Se prendiamo in
considerazione la funzione f (x-a), con a costante, questa assumerà lo stesso valore di f (x) nel punto "x+a" (infatti f ((x+a) - a) = f (x)).
Se prendiamo in
considerazione la funzione f (x-a), con a costante, questa assumerà lo stesso valore di f (x) nel punto "x+a" (infatti f ((x+a) - a) = f (x)).
Disegnandone il grafico si ottiene quindi la stessa curva, ma spostata verso destra sull'asse x.
Se la quantità a non è costante, la f (x a) diventa una funzione che "viaggia" lungo l'asse delle x:
![]() ONDA che si propaga nel verso
positivo dell'asse x
ONDA che si propaga nel verso
positivo dell'asse x
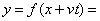 ONDA che si propaga nel verso
negativo dell'asse x
ONDA che si propaga nel verso
negativo dell'asse x
In generale una funzione del tipo: ![]() è la rappresentazione
matematica di un'onda periodica, nel caso particolare che la funzione dipenda
solo dalla variabile x.
è la rappresentazione
matematica di un'onda periodica, nel caso particolare che la funzione dipenda
solo dalla variabile x.
![]() Un caso particolare
di onda periodica è l'onda armonica, la cui
forma generale può essere espressa mediante la seguente equazione:
Un caso particolare
di onda periodica è l'onda armonica, la cui
forma generale può essere espressa mediante la seguente equazione: ![]()
![]() è la "fase dell'onda".
è la "fase dell'onda".
In generale noi non studieremo dei "singoli impulsi finiti", ma prenderemo in considerazione dei "treni d'onda infiniti" (ovviamente non riproducibili nella realtà).
Possiamo considerare due diversi tipi di periodicità:
Periodicità spaziale
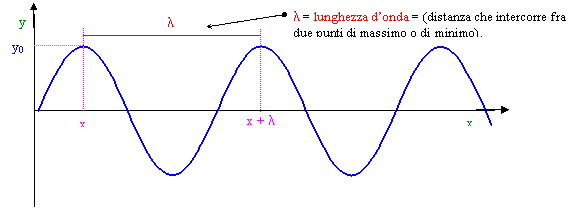 Rappresentiamo la
forma dell'onda in funzione dello spazio (nel nostro esempio consideriamo un'onda
armonica dipendente dalla sola variabile x)
in un certo istante t fissato.
Rappresentiamo la
forma dell'onda in funzione dello spazio (nel nostro esempio consideriamo un'onda
armonica dipendente dalla sola variabile x)
in un certo istante t fissato.
Consideriamo i due punti di massimo: ![]() e
e ![]()
Se chiamiamo ![]() e
e ![]() le due fasi dell'onda
e imponiamo
le due fasi dell'onda
e imponiamo ![]() , otteniamo:
, otteniamo: ![]() .
.
Quindi: ![]() (k = "numero d'onda").
(k = "numero d'onda").
Periodicità temporale
Rappresentiamo la forma dell'onda in funzione del tempo in un certo punto x fissato.
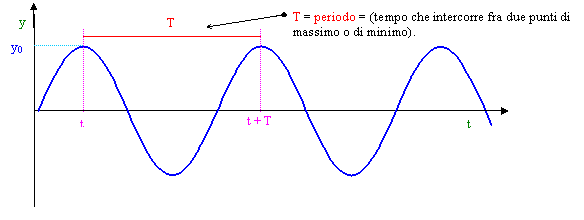
Consideriamo i due punti di massimo: ![]() e
e ![]()
Se chiamiamo ![]() e
e ![]() le due fasi dell'onda
e imponiamo
le due fasi dell'onda
e imponiamo ![]() , otteniamo:
, otteniamo: ![]() .
.
Quindi: ![]() .
.
Ma, per quanto detto in precedenza, si ha
anche ![]() e quindi:
e quindi: ![]() .
.
Velocità di fase dell'onda: 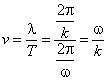 (T =
(T =![]() vedi moto armonico
vedi moto armonico
Equazione delle onde (equazione di D'Alambert)
Generica equazione di un'onda periodica che
si propaga lungo l'asse delle x: ![]() .
.
Poniamo: ![]() si ha:
si ha: ![]() e
e ![]() .
.
![]()
![]() Deriviamo " f "
rispetto a " x ":
Deriviamo " f "
rispetto a " x ": 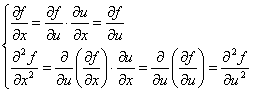
![]()
![]() Deriviamo " f "
rispetto a " t ":
Deriviamo " f "
rispetto a " t ": 

Risulta quindi evidente che: ![]()
 Più in generale,
cioè quando l'onda è funzione delle tre variabili x, y e z, si ottiene la seguente equazione di D'Alambert :
Più in generale,
cioè quando l'onda è funzione delle tre variabili x, y e z, si ottiene la seguente equazione di D'Alambert : 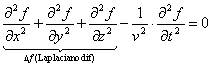
Onde piane
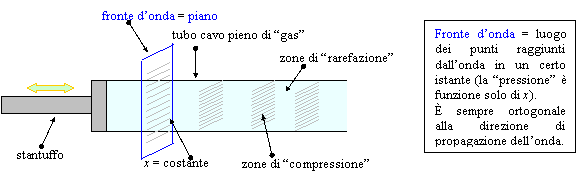
La superficie raggiunta dall'onda in ogni istante è costante. Nella realtà non esistono onde "perfettamente" piane (sono sempre leggermente "divergenti"), tuttavia, quando il raggio di curvatura è sufficientemente basso, si possono considerare piane. (es. raggi solari).
 Onde
sferiche
Onde
sferiche
In natura è quasi impossibile produrre un segnale perfettamente armonico in quanto sarebbe necessario generare un "treno infinito" di onde. Ad esempio le forme d'onda generate dai suoni dei diversi strumenti musicali sono dei segnali periodici, ma non di tipo armonico (cioè non possono essere espressi in modo semplice tramite le funzioni sen e cos). Una "approssimazione" di segnale armonico può essere ottenuta tramite un diapason.
Teorema di Fourier
Ogni suono "reale" può essere scomposto nella somma di tante componenti "sinusoidali" (teoricamente infinite) che prendono il nome di "armoniche" del suono stesso. La "prima armonica", cioè quella con frequenza più bassa, prende il nome di "suono fondamentale"; tutte le altre armoniche hanno frequenza che sono "multipli interi" della frequenza fondamentale.
Possiamo rappresentare un segnale periodico mediante la seguente formula (w = prima armonica):

![]()
(I coefficienti ai e bi dipendono dalla composizione spettrale del segnale).
Lezione 18 (16 novembre 1999)
Energia trasportata da un'onda
Ogni onda trasporta "energia" con la stessa velocità con la quale si propaga l'onda stessa.
L'energia trasportata da un'onda dipende dall'ampiezza della perturbazione e dalla pulsazione (w
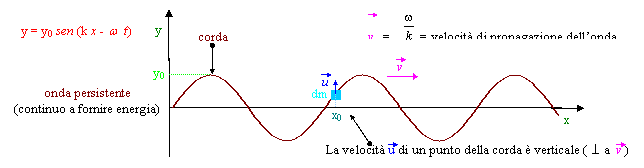
(Il punto di una corda, in funzione del tempo, si comporta in modo analogo a quello di un punto attaccato ad una molla che oscilla intorno al suo punto di equilibrio).
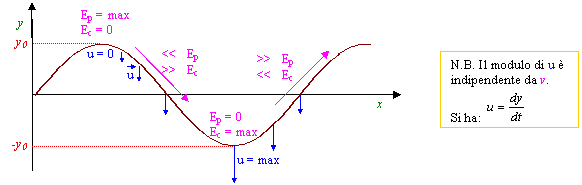
velocità
di un punto della corda: ![]()
Energia
cinetica di un elementino dm della corda ![]()
(![]() ).
).
Energia per unità di volume
(densità di energia): ![]()
Questa è una funzione "oscillante", quindi si tratta di un'energia di tipo "pulsante".
Nella realtà, noi percepiamo solo il "valore medio" di questa energia.
![]() Energia
cinetica media:
Energia
cinetica media: 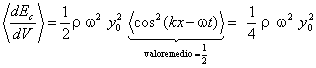
Densità media di energia associata a
un'onda: 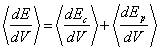 .
.
Il calcolo dell'energia potenziale media è però più complicato di quello effettuato per l'energia cinetica media; è simile ai calcoli effettuati per determinare l'energia potenziale di un corpo attaccato a una molla, ma in questo caso non è possibile associare una "costante elastica". Sappiamo comunque che la densità di energia potenziale è una funzione "oscillante" tra un valore minimo (pari a zero) e un valore massimo (pari al valore massimo assunto dalla densità di energia cinetica).
Si ha una continua trasformazione di energia cinetica in energia potenziale e viceversa. Possiamo quindi ragionevolmente ipotizzare che i due valori medi siano uguali.
Si ha quindi: ![]() (nel caso particolare considerato
dell'oscillazione di una corda)
(nel caso particolare considerato
dell'oscillazione di una corda)

In generale si può dimostrare che: ![]()
Cioè la densità media di energia trasportata da un'onda è proporzionale sia al quadrato della pulsazione sia al quadrato dell'ampiezza della perturbazione: a parità di pulsazione un raddoppio dell'ampiezza della perturbazione fa sì che l'energia trasportata dall'onda quadruplichi.
Intensità dell'onda (concetto legato all'energia)
In realtà non è tanto importante conoscere l'energia effettivamente trasportata da un'onda.
È più significativo determinare la quantità di energia che raggiunge il "ricevitore" ogni secondo.
 L'intensità è la quantità di energia che incide ogni
secondo su un metro quadro di superficie ortogonale alla direzione di
propagazione dell'onda (si misura in Watt/m2 = Joule/m2
sec).
L'intensità è la quantità di energia che incide ogni
secondo su un metro quadro di superficie ortogonale alla direzione di
propagazione dell'onda (si misura in Watt/m2 = Joule/m2
sec).
Intensità: 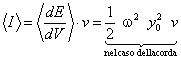 .
.
L'energia totale (cinetica e potenziale) trasportata da un'onda dipende solo dalla pulsazione dell'onda stessa e dall'ampiezza della perturbazione che ha generato l'onda: quindi è COSTANTE.
Nel caso di onde piane la superficie investita dall'onda è costante quindi lo è anche l'intensità.
Nel caso di onde sferiche la superficie investita dall'onda aumenta, man mano che ci si allontana dalla sorgente, proporzionalmente al quadrato della distanza. In questo caso l'intensità dell'onda non è più costante, ma decresce in modo proporzionale al quadrato della distanza dalla sorgente.
![]() Se indichiamo con P la potenza della sorgente si ha:
Se indichiamo con P la potenza della sorgente si ha: ![]() .
.
(Ricordando che l'intensità media è
proporzionale al quadrato dell'ampiezza della perturbazione possiamo ricavare
che quest'ultima è inversamente proporzionale al raggio, cioè: ![]() ).
).
Lezione 19 (22 novembre 1999)
PRINCIPIO DI SOVRAPPOSIZIONE E INTERFERENZA D'ONDE
Prendiamo in esame due perturbazioni ondose diverse (per esempio due sassi lanciati nell'acqua).
In ogni punto nel quale queste si "incontrano" (sovrappongono) si avrà una perturbazione pari alla somma delle due perturbazioni (tipico comportamento ondulatorio).
Interferenza di onde che si propagano nella stessa direzione
Consideriamo due onde "monocromatiche"
(composte da una "singola armonica") uguali (cioè con la stessa pulsazione w e lo stesso numero d'onda k): ![]() e
e ![]()
j rappresenta lo "sfasamento" fra le due onde che supponiamo costante nel tempo).
Immaginiamo che si incontrino in un
certo punto P dello spazio (la x è uguale per le due onde), la
perturbazione complessiva nel punto P
sarà: ![]() .
.
La "perturbazione massima" si ottiene quando le due onde si incontrano "in fase" (cioè j = 2np con n N). In questo caso si ha una "interferenza costruttiva".
La "perturbazione minima" si ha invece quando le due onde si incontrano in "opposizione di fase" (cioè j = (2n+1) p con n N). In questo caso si parla di "interferenza distruttiva".
Nel caso limite in cui ![]() le due onde si
annullano a vicenda.
le due onde si
annullano a vicenda.
Sono ovviamente possibili anche situazioni "intermedie".
Interferenza di onde emesse da sorgenti puntiformi
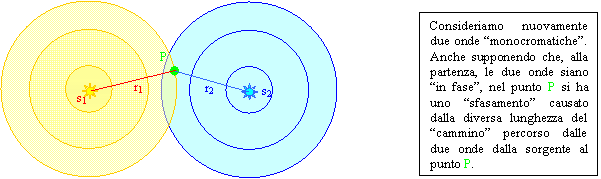
Nel punto P
si ha: ![]() e
e ![]() .
.
![]() Da cui:
Da cui: ![]()
Da quanto detto in
precedenza sappiamo che la massima interferenza costruttiva si ottiene
quando ![]()
Si ottiene un risultato analogo per la massima interferenza distruttiva:
![]()
Le "frange di interferenza" sono osservabili solo in presenza di "sorgenti coerenti", cioè di sorgenti che emettono onde con una fase ben definita in funzione del tempo (Dj resta costante). In presenza di "sorgenti incoerenti", nelle quali la fase varia in modo "casuale", (ad esempio nel caso delle normali lampadine a incandescenza) il fenomeno dell'interferenza non è visibile. Le intensità delle varie sorgenti si sommano in modo uniforme (invece di oscillare da zero alla somma dei massimi).
I BATTIMENTI (nel calcolo si
applica la seguente formula: ![]() )
)
Questo fenomeno si verifica in presenza di sorgenti di onde con pulsazioni "leggermente diverse":
![]() e
e ![]() con
con ![]() e
e ![]() .
.
Sommando le due onde si ha: ![]() .
.
![]() Se definiamo
Se definiamo ![]() e
e ![]() possiamo
scrivere:
possiamo
scrivere: ![]()
(il termine cos [...] prende il nome di "modulazione dell'ampiezza").
La differenza si fase non si mantiene costante: le due onde viaggiano con velocità diverse quindi lo sfasamento cambia in funzione del tempo.
La velocità con la quale "viaggia" la modulazione d'ampiezza prende il nome di velocità di gruppo.
Definiamo: ![]() e
e ![]() velocità
di gruppo =
velocità
di gruppo = ![]()
In sintesi si ha quindi: ![]() .
.
La distanza in tempo fra i battimenti è legata alla differenza dei valori k e w. La frequenza dei battimenti è tanto minore quanto più le due onde sono uguali.
Onde stazionarie
Consideriamo una corda fissata a un estremo in un punto "O" fisso e indeformabile: quando l'impulso arriva nel punto fisso subisce una riflessione e ritorna indietro con la stessa velocità.
Abbiamo quindi: 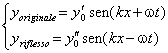 e, in O, si
ha:
e, in O, si
ha: ![]()
Supponendo che il punto O coincida con l'origine del sistema di riferimento
(cioè x = 0) otteniamo: ![]() .
.
Considerando che nel punto O si ha: ![]() , concludiamo che l'onda riflessa ha la stessa ampiezza e
velocità dell'onda incidente, ma risulta sfasata di p
, concludiamo che l'onda riflessa ha la stessa ampiezza e
velocità dell'onda incidente, ma risulta sfasata di p
![]()
![]() A questo punto la
perturbazione in ogni punto della corda sarà data dalla somma delle due onde:
A questo punto la
perturbazione in ogni punto della corda sarà data dalla somma delle due onde: ![]()
![]() ONDA STAZIONARIA (non è più un'onda che "viaggia").
ONDA STAZIONARIA (non è più un'onda che "viaggia").
Ha un'ampiezza che varia in funzione di x e una pulsazione che varia in funzione di t.

Consideriamo ora una corda
fissata ai due estremi:
Nei punti x = 0 e x = L (chiamati nodi) si ha: yoriginale + yriflessa = 0 da cui: y = 0.
Per x = 0 risulta sempre vero: x = 0 sen(kx) = 0 y = 0.
Per x = L invece la condizione y = 0 impone che sia sen(kL) = 0 cioè: kL = np
![]() Ricordando
che
Ricordando
che ![]() otteniamo la
condizione:
otteniamo la
condizione: ![]() in
una corda fissa agli estremi si possono formare solo onde stazionarie con
lunghezze d'onda ben precise (legate alla lunghezza della corda in base alla
relazione indicata). Le onde ottenuto assegnando a n progressivamente i valori 1, 2, . prendono il nome di prima armonica (o suono fondamentale),
seconda armonica, ..
in
una corda fissa agli estremi si possono formare solo onde stazionarie con
lunghezze d'onda ben precise (legate alla lunghezza della corda in base alla
relazione indicata). Le onde ottenuto assegnando a n progressivamente i valori 1, 2, . prendono il nome di prima armonica (o suono fondamentale),
seconda armonica, ..
Avendo "quantizzato" le lunghezze d'onda risultano predeterminate anche le relative frequenze:
![]() (la frequenza
minima si ottiene per n = 1 prima
armonica).
(la frequenza
minima si ottiene per n = 1 prima
armonica).
Le armoniche costituiscono le frequenze di oscillazione "naturali" di una corda (oscillazioni libere).
L'applicazione dall'esterno di impulsi con frequenze coincidenti a quelle naturali di un sistema (frequenze proprie) provoca il fenomeno della "risonanza" che aumenta notevolmente l'ampiezza delle oscilazioni rischiando di provocare seri problemi ( per esempio il crollo di un ponte sospeso).
Segnali
Soltanto un "treno infinito" di onde determina (tramite un'analisi di Fourier) una singola armonica.
Un segnale reale, invece, ha un inizio e una fine. Se effettuiamo l'analisi di Fourier di un segnale reale di durata Dt scopriamo che esso è composto da un insieme (teoricamente infinito) di onde tutte vicine a una determinata "frequenza principale" (fenomeno analogo a quello dei battimenti).
Un segnale, per propagarsi, ha bisogno di un "mezzo". Questo può essere dispersivo (se al suo interno onde con frequenza diversa si propagano a velocità diverse) o non dispersivo (se al suo interno tutte le onde si propagano con la stessa identica velocità).
In un mezzo non dispersivo tutte le componenti del segnale viaggiano alla stessa velocità, quindi il segnale non si deforma. In un mezzo dispersivo, invece, le frequenze più "alte" viaggiano più velocemente: le componenti del segnale viaggiano con velocità diverse, quindi il segnale si deforma durante la propagazione. In un segnale reale quindi non conta tanto la "velocità di fase" delle singoli componenti, quanto la "velocità di gruppo" con la quale si propaga l'intero segnale.
Un segnale contiene tante più armoniche
quanto più è corta la sua durata (![]() = costante).
= costante).
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025