|
|
| |
FONDAMENTI DI INFORMATICA I
CIRCUITI LOGICI
Rete che produce per ogni possibile combinazione dei suoi ingressi un valore della sua uscita.
Il valore dell'uscita dipende solamente dalla configurazione di valori presenti ai suoi ingressi all'istante considerato, e non dipende dalla storia precedente di tali valori.
L'uscita e' una funzione degli ingressi.
Una rete combinatoria può essere realizzata connettendo in maniera opportuna delle reti più semplici che costituiscono degli operatori elementari.
Un insieme di operatori elementari e' detto funzionalmente completo se e' possibile realizzare qualsiasi funzione combinatoria tramite gli operatori di tale insieme.
CIRCUITI LOGICI
Variabili logiche
I bit possono rappresentare i valori logici
vero (true) e falso (false)
con i livelli di segnale elettrico
H (high = 5V) e L (low = 0V)
Operatori logici
AND - prodotto logico *
OR - somma logica +
|
Si può dimostrare che con questi tre operatori sono esprimibili tutte le possibili funzioni logiche. |
NOT - negazione !
Le porte logiche rappresentano circuiti che forniscono in uscita il risultato di operazioni logiche elementari sui valori delle variabili in ingresso.
Tabelle della verità
Il risultato delle operazioni logiche, e quindi il comportamento delle porte logiche è in genere descritto mediante tabelle che elencano tutte le combinazioni dei valori di ingresso e il corrispondente valore del risultato.
PORTE LOGICHE
|
Simbolo
|
Porta AND - Prodotto logico A * B
|
Tabella della verità
|
B |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Porta OR - Somma logica A + B
|
Tabella della verità
|
B |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Simbolo
|
Porta NOT - Complemento !A
|
Simbolo
|
|
Tabella della verità
|
U |
|
|
|
|
|
|
|
|
|
|
FUNZIONI LOGICHE
Sono descrivibili con espressioni logiche
|
Tabella della verità
|
B |
S |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Es.
S = A * !B + !A * B
R = A * B
S vero se uno e uno solo di A e B è vero
R vero se entrambi A e B sono veri
Al fine di ridurre l'impiego delle parentesi nelle espressioni logiche e' definito il seguente ordine di priorità tra gli operatori elementari:
1) NOT 2) AND 3) OR
Es:l'espressione
A and not B or C
E' interpretata univocamente come
(A and (not B)) or C
Se una rete logica è una rete combinatoria, essa può essere sempre espressa tramite un'espressione di operatori logici.
Viceversa, data una qualsiasi espressione logica possiamo costruire una rete logica corrispondente
Utilizzando la corrispondenza tra espressioni logiche e reti logiche e' possibile trasformare una rete logica in un'altra equivalente applicando le leggi dell'algebra di Boole:
1) A and 1 = A 1') A or 0 = A
2) A and 0 = 0 2') A or 1 = 1
3) A and A = A 3') A or A = A
4) A and not A = 0 4') A or not A = 1
5) A and B = B and A 5') A or B = B or A
6) (A and B) and C = A and (B and C)
6') (A or B) or C = A or (B or C)
7) (A or B) and (A or C) = A or (B and C)
7') (A and B) or (A and C) = A and (B or C)
8) not (not A) = A
9) not A or not B = not (A and B)
Le funzioni logiche sono realizzabili circuitalmente (HW) mediante opportune connessioni (reti) di porte logiche
Primo esempio di rete logica (Semisommatore)
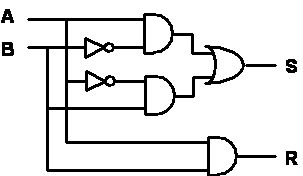
Si noti che la rete sopra rappresentata realizza la somma di due numeri binari ciascuno da un bit, dove A e B sono le cifre da sommare, S è la somma e R è il riporto.
Secondo esempio di rete logica
Tabella della verità (Sommatore completo)
|
A |
B |
RI |
S |
RO |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A e B |
|
|
|
|
|
|
sono le cifre degli addendi |
|
|
|
|
|
|
RI. |
|
|
|
|
|
|
è il riporto da cifra meno significativa |
|
|
|
|
|
|
RO. |
|
|
|
|
|
|
è il riporto verso cifra più significativa |
|
|
|
|
|
|
|
S = A*!B*!RI + !A*B*!RI + !A*!B*RI + A*B*RI
RO = A*B + A*RI + B*RI
|
|
La rete realizza la somma delle due cifre binarie (bit) di peso 2i in un numero di n bit, tenendo conto del riporto generato dalla somma dei due bit di peso 2i-1
Con n-1 reti di questo tipo più una rete come quella dell'esempio precedente e collegando in cascata i riporti uscenti RO con quelli entranti RI, si possono dunque sommare due numeri di n bit.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025