Introduzione

La capacità di risolvere problemi costituisce una delle componenti fondamentali della intelligenza umana ed ha rappresentato, storicamente, una delle prime abilità che si è cercato di trasfondere nei calcolatori. La prima difficoltà è stata dare una definizione precisa di problema. Duncker, nel 1963, lo ha così definito: «quando non è possibile passare dalla situazione in cui ci si trova alla situazione desiderata mediante una semplice azione (e cioè mediante l'esecuzione di operazioni del tutto ovvie) si fa ricorso al pensiero. Il compito del pensiero consiste nel concepire una certa azione che funga da mediatrice tra la situazione data e la situazione desiderata» [Duncker 1963].

In un primo momento l'attenzione della ricerca si è spinta verso la costruzione di programmi in grado di risolvere semplici giochi come gli scacchi, la dama o indovinelli basati sulla logica. Si pensava che l'applicazione di questi programmi potesse contribuire ed aumentare la comprensione di alcuni aspetti fondamentali delle capacità cognitive umane. Ben presto, però, 212j95c ci si è resi conto che, mentre è molto facile costruire programmi in grado di risolvere questi problemi, è particolarmente difficile realizzare programmi dotati di buon senso.

Nonostante ciò, giochi e rompicapi (problemi giocattolo) continuano ad essere utilizzati poiché mettono a disposizione situazioni semplici da rappresentare e manipolare.

L'insieme di tutti gli stati del problema viene detto spazio degli stati.

In alcuni casi può essere opportuno distinguere fra spazio degli stati, spazio problemico e spazio di ricerca.

Spazio degli Stati: Insieme degli stati teoricamente possibili in una data classe di problemi.

Spazio Problemico: Insieme degli stati che sono potenzialmente raggiungibili in una determinata situazione problemica.

Spazio di Ricerca: Insieme degli stati che vengono effettivamente raggiunti e presi in esame nel corso del processo di ricerca della soluzione.

Il secondo elemento fondamentale per descrivere un problema è l'operatore.

Un Operatore è una "mossa" o un'azione che permette di trasformare uno stato del problema in un nuovo stato.

Il punto di partenza per formalizzare problemi, in modo da poterli poi risolvere in modo automatico, consiste nell'identificare gli stati del problema e gli operatori utilizzabili per risolverlo.

Data una rappresentazione per gli stati e per gli operatori di una classe di problemi, uno specifico problema si definisce assegnando uno stato iniziale e uno stato finale. Definiremo come soluzione di un problema una sequenza di operatori che permetta di trasformare uno stato iniziale in uno stato finale.

In alcuni casi può non esistere un unico stato finale ma un insieme, più o meno ampio, di possibili stati finali. Qualora un problema ammetta diverse soluzioni si può essere interessati a trovare quella migliore.Stabilire quale sia la migliore soluzione può risultare a volte difficile in quanto i criteri di preferenza non sono sempre chiaramente definiti. La situazione si semplifica notevolmente se è possibile assegnare un costo ai vari operatori.

In molti casi risulta facile trovare una soluzione costosa e molto difficile trovare la soluzione ottima, spesso si ricorre a un compromesso.

DESCRIZIONE DEL GIOCO DELL'OTTO

Il gioco dell'otto utilizza otto tessere scorrevoli numerate da 1 a 8 racchiuse in una cornice quadrata. Una posizione nella cornice rimane vuota in modo tale da poter far scorrere le tessere che le stanno accanto. Il gioco consiste nel rimescolare a caso le varie tessere e nel risistemarle in ordine progressivo (di solito).

Con tale gioco, siamo praticamente in grado di costruire un gran numero di problemi, lo scopo di ognuno dei quali è quello di passare dalla configurazione attuale ad un'altra fino ad arrivare, poi, alla configurazione finale che rappresenta la soluzione al problema dato.

ESEMPIO 1

Possiamo stabilire che un problema nel gioco dell'otto è quello di avere le tessere con i numeri pari nella parte superiore del quadrato e quelle con i numeri dispari nella parte inferiore. Allora, in questo caso, è facile capire che c'è più di una soluzione per questo problema e quindi, non si ha un unico stato finale.

ESEMPIO 2

Supponiamo, di stabilire che un problema del gioco dell'otto è quello di avere le tessere ordinate da 1 a 8. Allora, in questo caso, si avrà un'unica soluzione per questo problema e quindi, un unico stato finale.

ESEMPIO 3

Sappiamo che lo spazio problemico è l'insieme degli stati raggiungibili da un certo stato; tale spazio problemico lo possiamo rappresentare mediante un grafo. Allora, la figura sottostante riporta un sottoinsieme dello spazio problemico nel gioco dell'otto rappresentato in forma di grafo.

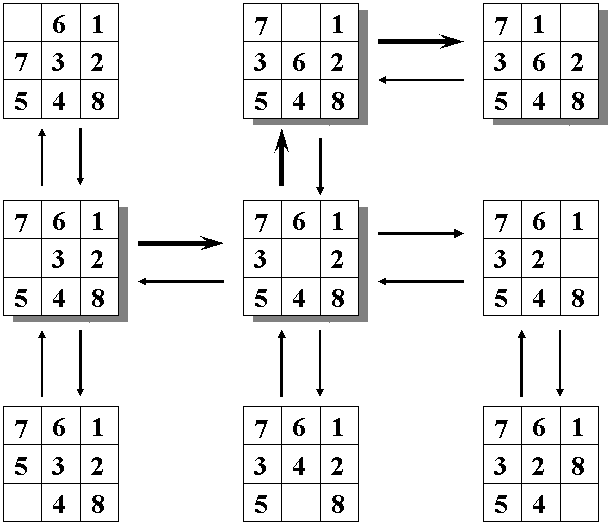
Nella figura abbiamo riportato, evidenziando le frecce in grassetto ed i nodi ombreggiati, un cammino che ci porta dallo stato iniziale allo stato finale.

Esistono diverse strategie in base alle quali è possibile effettuare una ricerca delle soluzioni:

partire dallo stato iniziale e per iterazioni successive raggiungere lo stato finale

partire dallo stato finale e per iterazioni successive raggiungere lo stato iniziale

partire contemporaneamente sia dallo stato iniziale che dallo stato finale e compiere una ricerca bidirezionale che ha termine quando i due percorsi si incontrano.

Un fattore da tener presente nella scelta della strategia è il cosiddetto fattore di ramificazione, cioè il numero di operatori che sono applicabili in ogni passo.

Una tecnica comunemente utilizzata nella ricerca della soluzione in uno spazio problemico costituita dal backtracking. L'idea di fondo su cui si basa il backtracking è la seguente:

Vai avanti con il processo di soluzione finché non raggiungi l'obiettivo desiderato o finché non puoi più proseguire.

Nel primo caso hai ottenuto quello che volevi ed il problema è risolto, nel secondo caso ritorna indietro (backtrack) ad un precedente punto di scelta e prendi in esame un'opzione diversa.

ESEMPIO 4

Supponiamo di essere interessati a stabilire se una certa persona, che indicheremo con A, sia discendente oppure no di un'altra persona, che indicheremo con B. Il problema verrebbe risolto in modo positivo se riuscissimo a trovare un legame di discendenza tra A e B. Ma questo legame come potremmo trovarlo? I modi potrebbero essere due:

Si parte da B, continuando con i suoi figli, i figli dei figli e così via, cioè facendo una ricerca in avanti, oppure

Si parte da A, si risale ai suoi genitori, poi ai suoi nonni etc., cioè facendo una ricerca all'indietro.

Il punto critico è dato dal fattore di ramificazione.

Supponiamo che da B ad oggi siano passate 15 generazioni. Poiché ogni persona ha due genitori, allora la ricerca che va da A per arrivare a B prenderà in considerazione 2¹⁵ antenati. Questo vuol dire che lo spazio problemico è formato da 2¹⁵ stati. Supponiamo invece, che il numero medio di figli avuti dalle persone vissute nelle 15 generazioni precedenti sia 4, il nostro spazio problemico sarà formato da 4¹⁵ stati. Allora, è facile capire che, in questo caso particolare, la ricerca all'indietro è quella più conveniente.

Le procedure usate per controllare il processo di ricerca si dividono in due grandi categorie:

procedure che applicano la ricerca cieca (blind search): lo stato da espandere viene scelto in base a un criterio che è fissato a priori e non dipende dalla qualità dello stato

procedure di ricerca euristica (heuristic search): lo stato viene scelto sfruttando le informazioni che si hanno a disposizione sul dominio in modo da espandere per primi gli stati che appaiano più promettenti.

ESEMPIO 5

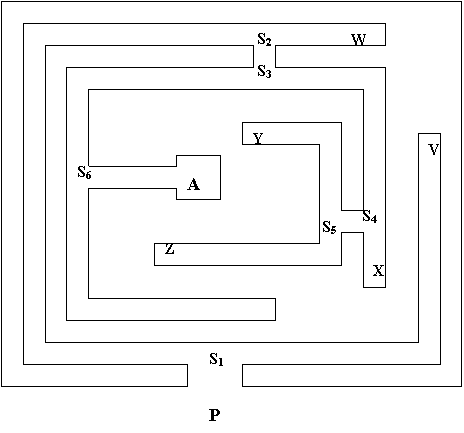
Consideriamo di risolvere il problema rappresentato dal voler trovare una strada che da un punto di partenza ci porti ad un punto di arrivo in un labirinto. Gli stati del problema sono costituiti dalle diverse posizioni che si possono occupare all'interno del labirinto. Nel labirinto il punto P (partenza) rappresenta lo stato iniziale, mentre lo stato finale viene raggiunto se si arriva nel punto A (arrivo). Gli operatori che possiamo usare per risolvere il problema coincidono con le diverse direzioni che si possono prendere davanti ad un bivio:

Nord

Sud

Est

Ovest

Supponiamo che una volta presa una direzione, si continui fino al prossimo punto di scelta o finché non si arriva in un punto cieco. Vediamo cosa accade quando vogliamo risolvere tale problema.

Nel momento in cui varchiamo il punto P ci troviamo subito di fronte al primo punto di scelta che è S₁. Supponiamo di voler andare verso est; si segue questa strada finché non si giunge all'ostacolo V; a questo punto, non potendo andare avanti, facciamo backtracking e ritorniamo al punto S₁; da qui è inutile prendere la strada verso sud poiché si ritornerebbe al punto P, allora si va verso ovest. Da qui si va avanti finché non arriviamo al punto S₂. Verso nord non possiamo andare allora, si va avanti verso est finché non ci troviamo di fronte l'ostacolo W. Ora, siamo costretti a

fare di nuovo backtracking e torniamo così al punto S₂; da qui prendiamo la direzione verso sud. Arrivati nel punto S₃ ci si chiede quale strada prendere. La direzione verso nord è da escluderla perché in questo caso torneremo indietro. Allora prendiamo la strada verso est e arriviamo così nel punto di scelta S₄. Si continua in questo modo ad andare avanti e a fare backtracking finché non arriviamo al punto A.

Nella figura successiva mostriamo in forma schematica lo spazio di ricerca esplorato nel tentativo di arrivare al punto A. Lo spazio di ricerca è stato rappresentato mediante un albero.

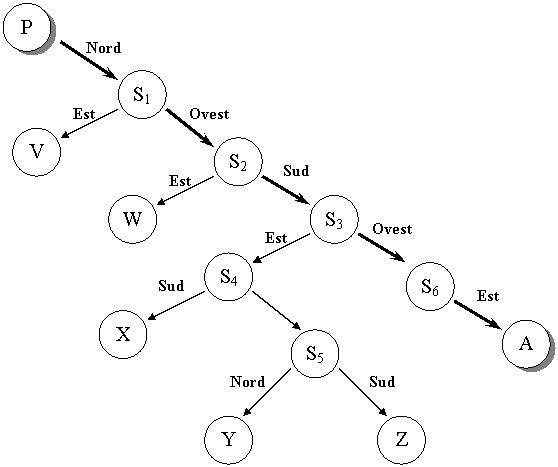
In grassetto, sull'estrema destra della figura, è illustrato un cammino di soluzione per il nostro problema. La soluzione rappresentata dal nodo (stato) A è stata ottenuta applicando 5 operatori distinti:

in P - vai a nord

in S₁ - vai ad ovest

in S₂ - vai ad sud

in S₃ - vai ad ovest

in S₆ - vai ad est.

Il processo di risoluzione dei problemi è in gran parte identificabile e riconducibile a un processo di ricerca.

Ricerca cieca

Questo modo di procedere rappresenta evidentemente quanto di meno intelligente si possa immaginare, infatti la ricerca cieca risulta inefficiente nel caso di problemi di complessità realistica. Lo studio di queste procedure è comunque importante per tre ordini di motivi:

esse rappresentano dei metodi estremamente generali che si possono applicare sempre e comunque, anche in assenza di qualsiasi informazione sulla natura del problema che ci si trova ad affrontare

sono delle procedure di base che stanno a fondamento di altre procedure più sofisticate che derivano da esse e ne costituiscono spesso una variante

forniscono gli standard in base ai quali vengono valutate le prestazioni di altre procedure più efficienti.

Abbiamo diversi tipi di ricerche cieche, che si differenziano per costi e robustezza.

Ricerca in profondità

Questo tipo di approccio si basa sull'idea di espandere di volta in volta uno degli stati che sono stati generati nella mossa immediatamente precedente.

Il motivo per cui la ricerca in profondità ha questo nome è dato dal fatto che ad ogni passo la procedura espande un figlio di uno dei nodi che sono stati appena generati. Come conseguenza, una volta scelto un cammino, lo segue a livelli di profondità sempre crescenti finché o si trova la soluzione o si raggiunge un punto cieco (nel qual caso si attua il backtracking cronologico). Di seguito viene presentata una prima versione dell'algoritmo di ricerca in profondità.

DESCRIZIONE DEL PROBLEMA DEI FIAMMIFERI

Dati n fiammiferi suddivisi in m gruppi di diversa cardinalità, il problema dei fiammiferi consiste nell'ottenere m gruppi della stessa cardinalità attraverso degli opportuni spostamenti.

Lo spostamento dei fiammiferi deve rispettare la regola: "è possibile spostare dei fiammiferi dal mucchio A al mucchio B, solo se B raddoppia il suo numero di fiammiferi".

Notiamo, che n, il numero dei fiammiferi, deve essere pari a m*k (con k appartenente ad N).

ESEMPIO 6:

Dati 12 fiammiferi ripartirti in tre mucchi distinti, rispettivamente di 4, 7 e 1 fiammifero il problema consiste nel ripartire equamente i fiammiferi nei tre mucchi.

Lo stato iniziale è <4,7,1> mentre, quello finale, è <4,4,4>.

Gli operatori possono essere stabiliti in questo modo:

(a)   sposta n fiammiferi dal primo mucchio al secondo ,

(b)  sposta n fiammiferi dal primo mucchio al terzo ,

(c)   sposta n fiammiferi dal secondo mucchio al primo ,

(d)  sposta n fiammiferi dal secondo mucchio al terzo ,

(e)   sposta n fiammiferi dal terzo mucchio al primo,

(f)    sposta n fiammiferi dal terzo mucchio al secondo .

Supponiamo che la ricerca avvenga in avanti e che gli operatori siano applicati nell'ordine sopra indicato.

La seguente figura illustra lo spazio di ricerca generato dalla procedura di ricerca in profondità e il cammino di soluzione trovato da questa:

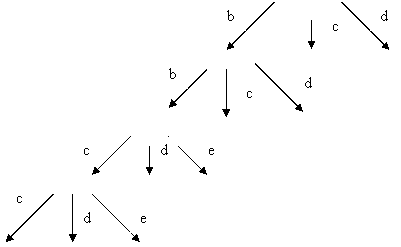<4,7,1>

<3,7,2> <8,3,1> <4,6,2>

<1,7,4> <6,4,2> <3,5,4>

<2,6,4> <1,3,8> <2,7,3>

<4,4,4> <2,2,8> <4,6,2>

Dalla figura si osserva che la procedura in ogni passo espande un figlio di uno dei nodi appena generati. Di conseguenza, una volta scelto il cammino, lo si esegue a livello di profondità crescente finché o si trova la soluzione o si raggiunge un punto cieco e quindi si applica il backtracking

ALGORITMO 1: ricerca in profondità (prima versione).

0.Accertati che la lista sia vuota.

1.Inserisci il nodo radice nella lista.

2.SE non ci sono più nodi nella lista

ALLORA fermati: la procedura ha fallito.

3.SE il nodo all'inizio della lista è un nodo finale ,

ALLORA fermati hai risolto il problema.

4.SE il nodo all'inizio della lista non ha figli

ALLORA toglilo dalla lista,

ALTRIMENTI sostituisci tale nodo con i suoi figli (ordinati

secondo il criterio che hai deciso di seguire)inserendoli all'inizio

della lista stessa.

5.Ritorna al passo 2.

DIFETTI:

anche se trova una soluzione non è detto che questa sia quella ottima.

Difatti guardando la precedente figura se si effettua come prima mossa la d si giunge allo stato <4,6,2> con la seconda mossa spostando 2 fiammiferi dal secondo al terzo mucchio si arriva allo stato finale.

Potrebbe non trovare la soluzione anche se questa esiste. Ciò si ha quando si entra in loop, così per esempio nella figura seguente si passa da <0,8,4> a <0,4,8> continuamente.

ALGORITMO 2: ricerca in profondità (con detenzione cicli).

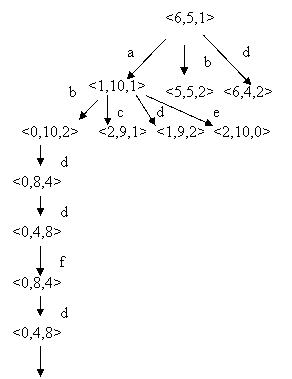
0.Accertati che le due liste aperti e chiusi siano vuote.

1.Inserisci il nodo radice nella lista aperti.

2.SE non ci sono più nodi nella lista aperti

ALLORA fermati: la procedura ha fallito.

3.SE il nodo all'inizio di aperti è un nodo finale ,

ALLORA fermati hai risolto il problema.

4.SE il nodo all'inizio di aperti non ha figli OPPURE

il nodo compare già nella lista chiusi

ALLORA toglilo dalla lista,

ALTRIMENTI

4 a. Sostituisci il nodo all'inizio di aperti con i suoi figli

(ordinati secondo il criterio che hai deciso di seguire)

e inseriscili all'inizio di aperti .

4 b. Inserisci il nodo che hai appena tolto da aperti nella lista chiusi.

5.Ritorna al passo 2.

OSSERVAZIONI:

evita di entrare in loop infinito usando le due liste:

lista aperti in cui vi sono i nodi in attesa di espansione

lista chiusi in cui vi sono i nodi già espansi.

Un nodo non viene più riesaminato se è un nodo foglia o se è nella lista chiusi.

SIMULAZIONE: facendo riferimento alla figura precedente l'algoritmo effettua i seguenti passi:

PASSO 0: aperti [ ] ,chiusi [ ]

PASSO 1: aperti [<6,5,1> ] ,chiusi [ ]

PASSO 2: aperti[<1,10,1> <5,5,2> <6,4,2> ] ,chiusi [<6,5,1> ]

PASSO 3: aperti [<0,10,2> <2,9,1> <1,9,2> <2,10,0> <5,5,2> <6,4,2>],

chiusi [<1,10,1> <6,5,1> ]

PASSO 4: aperti [<0,8,4> <2,9,1> <1,9,2> <2,10,0> <5,5,2> <6,4,2>],

chiusi [<0,10,2> <1,10,1> <6,5,1> ]

PASSO 5: aperti [<0,4,8> <2,9,1> <1,9,2> <2,10,0> <5,5,2> <6,4,2>],

chiusi [<0,8,4> <0,10,2> <1,10,1><6,5,1> ]

PASSO 6: aperti[<0,8,4> <2,9,1> <1,9,2> <2,10,0> <5,5,2> <6,4,2>],

chiusi[<0,4,8> <0,8,4> <0,10,2> <1,10,1> <6,5,1> ]

A questo punto l'algoritmo toglie <0,8,4> dalla lista aperti poiché si accorge di averlo già visitato, in quanto presente in entrambe le liste e quindi passa ad espandere <2,9,1>.

DIFETTO: se lo spazio problemico è infinito non è detto che si trovi la soluzione in quanto la procedura potrebbe perdersi ad indagare nodi situati a livelli di profondità sempre crescenti senza raggiungere uno stato finale. Ciò si può notare con il seguente esempio:

supponiamo di voler trovare tre numeri naturali tali che il terzo sia uguale alla somma dei primi due, ossia denotando con a, b, c i tre numeri vogliamo che a+b=c. Rappresentiamo un nodo dello spazio degli stati con una terna e consideriamo come operatori l'incremento di una unità relativo rispettivamente al primo ,secondo e al terzo numero della terna .

Stabiliamo di applicare gli operatori nell'ordine sopra citato, lo stato iniziale è <1,1,1> e ogni nodo capace di soddisfare l'equazione data è un nodo finale.

Applicando la procedura passiamo da <1,1,1> a <2,1,1> quindi a <3,1,1> e così via, quindi non giungeremo mai ad una soluzione.

ALGORITMO 3: ricerca a profondità limitata.

0.Accertati che la lista sia vuota e poni p uguale al limite

di profondità prefissato.

1.Inserisci il nodo radice nella lista.

2.SE non ci sono più nodi nella lista

ALLORA fermati: la procedura ha fallito.

3.SE il nodo all'inizio della lista è un nodo finale ,

ALLORA fermati hai risolto il problema.

4.SE il nodo all'inizio della lista non ha figli OPPURE

il nodo ha un valore di profondità uguale a p

ALLORA toglilo dalla lista,

ALTRIMENTI sostituisci tale nodo con i suoi figli (ordinati

secondo il criterio che hai deciso di seguire) inserendoli

all'inizio della lista stessa.

5.Ritorna al passo 2.

OSSERVAZIONE: i cicli non causano problemi poiché non scendiamo oltre il limite di profondità prefissato p.

DIFETTO: è necessario indicare a priori il limite p entro il quale va cercata la soluzione. Quindi se p è più piccolo del cammino di soluzione più breve, la ricerca fallisce. Se invece p è troppo grande la procedura rischia di sprecare tempo esplorando cammini inutili prima di arrivare alla soluzione.

ALGORITMO 4: ricerca per approfondimento iterativo.

0.Accertati che la lista sia vuota e poni il limite corrente c uguale a 1.

1.Inserisci il nodo radice nella lista.

2.SE non ci sono più nodi nella lista

ALLORA

2 a. Incrementa di 1 il valore di c.

2 b. Ritorna al passo 1.

3.SE il nodo all'inizio della lista è un nodo finale ,

ALLORA fermati hai risolto il problema.

4.SE il nodo all'inizio della lista non ha figli OPPURE

il nodo ha un valore di profondità uguale a c

ALLORA toglilo dalla lista,

ALTRIMENTI sostituisci tale nodo con i suoi figli (ordinati

secondo il criterio che hai deciso di seguire) inserendoli

all'inizio della lista stessa.

5.Ritorna al passo 2.

OSSERVAZIONE: cerca di evitare i difetti dell'algoritmo precedente utilizzando un limite di profondità variabile c.

DIFETTO: ogni volta che aumenta il limite c la procedura riesegue il lavoro già fatto espandendo nuovamente gli stati che rientravano nel limite precedente.

Ricerca per Ampiezza

L'altra fondamentale procedura di ricerca cieca è la ricerca per ampiezza.

Nella ricerca per ampiezza un nodo di un dato livello viene esaminato solo dopo che sono stati esaminati tutti quelli del livello precedente.

Se confrontiamo tale algoritmo con quello della ricerca in profondità ci accorgiamo che essi sono praticamente identici l'unica differenza è riscontrabile nel passo 4 e riguarda il modo nel quale i figli del nodo che è stata espanso vengono inseriti nella lista dei nodi da visitare. Nella ricerca in profondità i nodi vengono inseriti all'inizio della lista, nella ricerca per ampiezza i nodi sono inseriti alla fine della lista stessa.

Va fatto notare come la ricerca per ampiezza risulti notevolmente più robusta di quella in profondità. In primo luogo la procedura è sempre in grado di trovare una soluzione, posto che questa esista. In secondo luogo con questa procedura non è necessario ricorrere al backtracking, infine la ricerca per ampiezza garantisce che venga trovato per primo il cammino di soluzione più corto, vale a dire quello ottenibile applicando il minor numero di operatori.

Il prezzo che bisogna pagare per questa robustezza è comunque elevato e fa si che la procedura risulti in pratica inusabile nel caso di problemi di complessità realistica.

ALGORITMO 5: ricerca per ampiezza

Accertati che la lista sia vuota.

Inserisci il nodo radice nella lista.

SE non ci sono più nodi nella lista

ALLORA fermati: la procedura ha fallito.

SE il nodo all'inizio della lista è un nodo finale

ALLORA fermati: hai risolto il problema.

SE il nodo all'inizio della lista non ha figli,

ALLORA toglilo dalla lista,

ALTRIMENTI sostituisci tale nodo con i suoi figli (ordinati secondo il criterio che hai deciso di seguire) inserendoli alla fine della lista stessa.

Ritorna al passo 2.

Di recente è stata proposta una nuova procedura di ricerca cieca dalle interessanti proprietà chiamata allargamento iterativo.

Questa procedura attua una ricerca limitata per ampiezza nella quale si aumenta gradualmente il limite fino al rinvenimento della soluzione. In altre parole, si parte con un limite di ampiezza A rappresentante il numero massimo di figli di ciascun nodo che è possibile prendere in considerazione prima di fare il backtracking. Qualora si siano esplorati inutilmente A figli di un dato nodo N, il nodo viene abbandonato anche se esistono altri figli di N che devono essere ancora esplorati. Qualora la soluzione non venga trovata all'interno del limite A considerato, questi viene gradualmente aumentato finchè si arriva alla soluzione o si sono esaurite le risorse a disposizione. La procedura limita gli esiti di possibili errori riducendo la portata della ricerca che viene eseguita sui figli di ciascun nodo.

ALGORITMO 6: ricerca per allargamento iterativo

Accertati che la lista sia vuota, e poni il limite corrente di ampiezza a uguale a 2.

Inserisci il nodo radice nella lista.

SE non ci sono più nodi nella lista

ALLORA

2a. Incrementa di 1 il valore di a.

2b. Ritorna al passo 1.

SE il nodo all'inizio della lista è un nodo finale

ALLORA fermati: hai risolto il problema.

SE il nodo all'inizio della lista non ha figli,

ALLORA toglilo dalla lista,

ALTRIMENTI sostituisci tale nodo con i suoi primi a figli (ordinati secondo il criterio che hai deciso di seguire) inserendoli all'inizio della lista stessa.

Ritorna al passo 2.

ESEMPIO 8

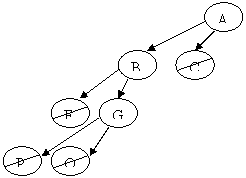
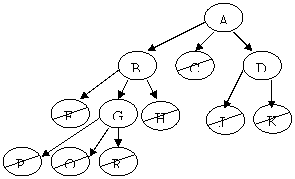
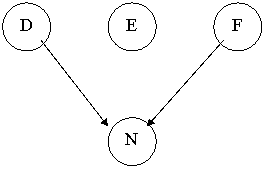
La figura mostra un ipotetico spazio di ricerca visitato dalla procedura nel corso delle successive iterazioni. I nodi barrati rappresentano dei nodi foglia che non costituiscono uno stato finale. Una volta raggiunto un nodo di questo tipo, non si può più proseguire e bisogna fare backtracking. Il nodo ombrato rappresenta, invece, uno stato finale.

Nella prima iterazione si parte con limite a=2. Vengono esaminati due figli di ogni nodo ma ciò non è sufficiente a trovare la soluzione. Nell'iterazione successiva, il limite viene portato a tre. I nodi già visitati vengono riesaminati mentre si aumenta il numero dei figli presi in considerazione per ciascun nodo. Anche in questo caso, la ricerca termina con un fallimento. Nell'ultima iterazione (con a=4) si riesce finalmente a raggiungere il nodo N che è un nodo finale.

			a=2

			a=3

Ricerca in Alberi And/Or

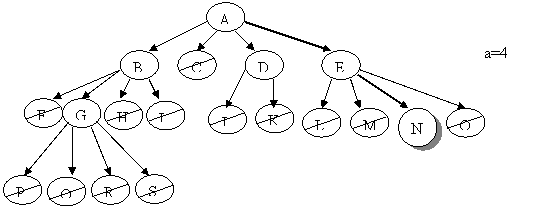
Finora il processo di risoluzione dei problemi è stato visto in termini di rinvenimento di un cammino di soluzione all'interno di uno spazio problemico rappresentabile in forma di grafo. I nodi di tale grafo erano costituiti dagli stati del problema, gli archi stavano a denotare l'applicazione di diversi operatori.

Esiste però un diverso modo di rappresentare lo spazio di ricerca basato su una differente concettualizzazione del processo di problem solving. In questa nuova prospettiva, un problema viene risolto scomponendolo in sottoproblemi più semplici ciascuno dei quali viene a sua volta scomposto in ulteriori sotto problemi fino ad arrivare ad una serie di sottoproblemi elementari.

ESEMPIO 9

PROBLEMA DELLA CENA

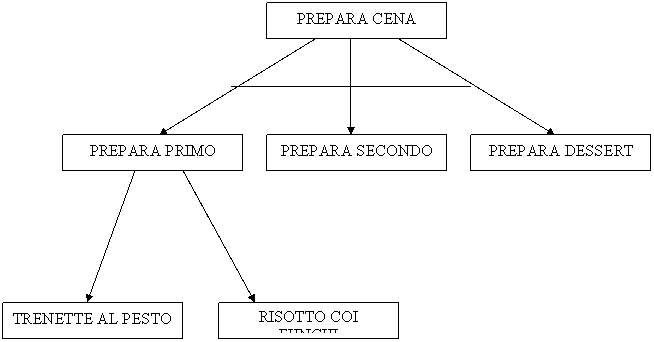
Supponiamo che il nostro problema sia quello di preparare una buona cena.

Questo problema può essere scomposto in tre sottoproblemi distinti.

1. preparare il primo;
2. preparare il secondo;
3. preparare il dessert.

Per riuscire a preparare una buona cena (e quindi a risolvere il problema), devo essere in grado di risolvere tutti e tre i sottoproblemi (NODI AND).

Consideriamo ora il problema del primo; supponiamo di avere come scelta trenette al pesto o risotto coi funghi.

Quindi il problema di preparare il primo a sua volta può essere scomposto in due sottoproblemi:

1. trenette al pesto;
2. risotto coi funghi.

In questo caso basta risolvere uno dei sottoproblemi (NODO OR) per risolvere il problema da cui sono stati generati.

Prendiamo in considerazione il problema dato dal preparare le trenette al pesto;

possiamo ancora suddividere questo problema in due sottoproblemi:

1. cuoci trenette
2. aggiungi pesto.

Notiamo che per risolvere il problema delle trenette al pesto, si devono risolvere entrambi i problemi.

Cuoci trenette può essere considerato come un problema primitivo immediatamente risolvibile.

Aggiungi pesto può essere a sua volta suddiviso in:

1. compra pesto;
2. prepara pesto.

Compra pesto può essere considerato come un problema primitivo, e prepara pesto può essere a sua volta suddiviso in sottoproblemi.

Lo stesso metodo viene applicato a tutti i nodi dell'albero.

PROCURA OLIO

PROCURA PINOLI

PROCURA BASILICO

COMPERA PESTO

PREPARA PESTO

AGGIUNGI PESTO

CUOCI TRENETTE

Questo approccio si rivela molto efficace qualora i sottoproblemi siano indipendenti e possano quindi essere risolti in maniera autonoma uno dall'altro.

La struttura che si ottiene ragionando in questo modo viene detto albero dei sottoproblemi o albero AND/OR.

In un albero AND/OR troviamo due tipi di nodi. I nodi corrispondenti a problemi la cui risoluzione richiede che vengano risolti tutti i sottoproblemi figli sono detti nodi AND, quelli corrispondenti a problemi la cui risoluzione viene ottenuta risolvendo almeno uno dei figli sono detti nodi OR (per convenzione si usa collegare i figli di un nodo AND con un segmento o con un arco).

I nodi foglia di un albero AND/OR rappresentano i problemi terminali e possono essere:

problemi primitivi (immediatamente risolti)

problemi irrisolvibili (problemi che non sono primitivi e che non possono essere ulteriormente decomposti)

Quindi dato un albero AND/OR che ha per radice il problema da risolvere, si considera come soluzione del problema qualsiasi sottoalbero che parta dalla stessa radice e i cui nodi siano tutti risolvibili.

Un nodo si dice risolvibile se:

corrisponde ad un nodo primitivo

è un nodo OR avente almeno un nodo figlio risolvibile

è un nodo AND avente tutti i nodi figli risolvibili

Il punto critico nell'applicazione di questo metodo di soluzione consiste nel trovare il modo per scomporre un dato problema in sottoproblemi più semplici. Mentre gli operatori che si usano nella metodologia dello spazio degli stati rappresentano semplicemente le "regole del gioco", gli operatori di riduzione utilizzati con il metodo della riduzione a sottoproblemi si fondano su un'analisi compiuta dal programmatore e rappresentano parte delle conoscenze che il programmatore ha sul modo di risolvere il problema.

Limiti della ricerca cieca

Un fattore critico, nel valutare la possibilità di usare o meno una data procedura per risolvere una classe di problemi, è costituito dall'efficienza con la quale la procedura riesce a raggiungere la soluzione.

Due elementi molto importanti utilizzati nel valutare l'efficienza di una procedura sono rappresentati dal tempo necessario alla procedura per risolvere un problema e dallo spazio di cui la procedura ha bisogno per immagazzinare i dati necessari a raggiungere la soluzione.

Procedure di ricerca euristica

Un altro dominio che, per la complessità del suo spazio dei problemi, risulta intrattabile con la ricerca cieca è il gioco degli scacchi. Quanto è grande lo spazio problemico degli scacchi? E' possibile farne una stima, almeno come ordine di grandezza ? La posizione iniziale del gioco è fissata dal regolamento. La mossa iniziale tocca al bianco che ha a disposizione 20 modi diversi per effettuarla. La risposta tocca al nero il quale ha anch'esso a disposizione 20 possibili mosse. In generale, tuttavia, il numero di mosse legali a disposizione di un giocatore in una qualsiasi fase del gioco che non sia la mossa iniziale è superiore a venti, diciamo sulla trentina. Per ogni turno di gioco (mossa del bianco e contromossa del nero) sono dunque possibili all'incirca un migliaio di mosse differenti (30 mosse del bianco ciascuna delle quali può essere seguita da 30 contromosse del nero; 30*30 all'incirca 1000). Tenendo presente che una partita dura mediamente una quarantina di turni, si può stimare che lo spazio problemico sia costituito da 1000⁴⁰ (cioè 10¹²⁰) diversi cammini -un numero astronomico che non riusciamo nemmeno ad immaginare (tanto per dare un'idea: l'età dell'universo è stimabile nell'ordine di 10¹⁶ secondi!).

Giocare a scacchi con una ricerca cieca di tutte le diverse mosse è quindi semplicemente impossibile. Anche attuare un'analisi completa che prenda in considerazione più di tre o quattro turni di gioco risulta estremamente difficile. Un bravo scacchista non gioca usando una ricerca cieca ma sfruttando una serie di principi di carattere generale:

evitare di concedere all'avversario un vantaggio di pezzi,

sviluppare rapidamente i propri pezzi,

arroccare prima possibile,

controllare le caselle centrali,

porre le proprie torri su colonne libere,

porre gli alfieri sulle diagonali principali,

tenere i cavalli al centro della scacchiera

ecc. Seguendo questi consigli non è detto che si ottenga una vittoria sicura (altrimenti gli scacchi perderebbero il loro fascino) ma certamente si vinceranno più partite seguendo questi consigli piuttosto che rifiutando di comportarsi nel modo suggerito.

Consigli come quelli visti in precedenza vengono detti tecnicamente euristiche. Le euristiche rappresentano dei criteri per decidere quale opzione, fra le diverse possibili, risulta più promettente per raggiungere un determinato obiettivo. Un euristica può venir considerata come un " trucco " per guidare le espressioni di un individuo. Lo studio delle euristiche trae la sua aspirazione dall'osservazione di quanto gli individui riescono a fare in base ad un insieme di conoscenze - né complete né corrette - alle quali ci si riferisce con altri termini come intuito " intuito ", " esperienza"," mestiere" ed altri ancora. Nel risolvere problemi raramente si hanno a disposizione tutte le informazioni necessarie e, ancora più di rado, si è in grado di trovare la migliore soluzione possibile. Una buona euristica fornisce un modo semplice per stabilire cosa fare in una determinata situazione. Anche se non garantisce che la scelta fatta sia la migliore, essa funziona bene nella maggior parte dei casi. Le euristiche rappresentano spesso l'unico modo per risolvere problemi complessi che richiederebbero la valutazione di un numero immenso di possibilità. Esse dunque permettano di limitare drasticamente il numero delle possibili alternative e di ottenere una soluzione sensata entro limiti di tempo ragionevoli. Il modo semplice più di sfruttare le euristiche nel processo di ricerca della soluzione consiste nell'uso di qualche funzione euristica.

Una funzione euristica è una regola un procedimento che assegna ad ogni stato problemico un numero rappresentante una misura di " bontà " di tale stato. La funzione euristica viene usata per valutare i diversi stati problemici e per determinare quanto essi siano desiderabili. Tale informazione viene sfruttata nello scegliere di volta in volta lo stato da espandere.

Per tornare all'esempio degli scacchi, la funzione euristica usata da un programma che giochi a scacchi terrà conto dei principi descritti in precedenza nel calcolare il valore di una determinata posizione. In ogni turno di gioco il programma sceglierà la mossa che porta alla posizione ritenuta migliore in base al valore attributo della funzione euristica. E' ovvio che il calcolare una tale funzione sarà un processo piuttosto complesso ed è altrettanto ovvio che , quanto migliore è la funzione euristica utilizzata, tanto più brillante sarà lo stile di gioco esibito dal programma.

Ritornando a domini più formali, prendiamo in esame alcune funzioni euristiche che possono venir applicate al gioco del lotto.

ESEMPIO 11

Consideriamo la seguente situazione:

Stato iniziale

Stato finale 

A

B

C

Prima euristica

Preso un nodo n, f(n) sarà dato dal numero di tessere che devono cambiare posizione. Uno stato n sarà considerato tanto più promittente quanto minore è valore di f(n).

Nell'esempio sopra f(A)=2 (la posizione più favorevole), f(B)=3 e f(C) =4.

Seconda euristica

Preso un nodo n, f'(n) sarà calcolato sommando la distanza di Manhattan (numero di spostamenti orizzontali e verticali necessari per raggiungere la posizione voluta) delle varie tessere dalla loro posizione finale.

Nell'esempio sopra f'(A)=2 (ancora la posizione più favorevole), f'(B)=4 e f'(C) =4.

Terza euristica

Preso un nodo n, f''(n) sarà ottenuto moltiplicando per 3 il punteggio di sequenza. Cioè f''(n)=3xseq(n) dove seq(n) si calcola sommando i seguenti valori delle tessere:

1 se la tessera è centrale

2 se la tessera è sui bordi ed è seguita in senso orario dalla tessera che la segue nella posizione finale

0 se la tessera è sui bordi ed è seguita in senso antiorario dalla tessera che la segue nella posizione finale

Nell'esempio sopra f''(A)=15 visto che seq(A)=5, f''(B)=18 con seq(B)=6 e f''(C) =15 con seq(C)=15.

Sia A che C risultano le scelte migliori.

Lo scopo di una funzione euristica è dunque quello di guidare il processo di ricerca nella direzione più favorevole, suggerendo il cammino più promettente fra un insieme di possibili cammini. Occorre tener presente comunque che, in linea di massima, quanto più un euristica è sofisticata, tanto più costoso il calcolo della sua funzione.

Avere una funzione euristica è comunque utile se siamo in grado di utilizzarla. Gli algoritmi che verranno presentati in seguito sono in grado di usare tali funzioni eseguendo una ricerca euristica

Hill Climbing

La prima procedura di ricerca euristica che prenderemo in considerazione è la cosiddetta procedura di Hill climbing. Questa procedura è estremamente semplice e rappresenta uno dei più diffusi modi di risolvere problemi. la procedura è basata sul concetto di ottimizzazione locale e sfrutta informazioni di natura euristica per procedere in modo incrementale verso la soluzione. Il nome fa riferimento al fatto che il comportamento della strategia è paragonabile al comportamento di un alpinista che, posto di fronte ad un bivio, per raggiungere la cima del monte scelga sempre il sentiero che va verso l'alto.

ALGORITMO 7

Considera il nodo radice come nodo corrente.

SE il nodo corrente è un nodo finale ALLORA fermati: hai risolto il problema.

SE il nodo corrente non ha figli: ALLORA fermati: la procedura ha fallito.

Espandi il nodo corrente e calcola il valore della  funzione euristica per tutti i suoi figli.

Scegli il nodo figlio avente il miglior valore di funzione euristica.

SE tale nodo ha un valore euristico peggiore del nodo corrente ALLORA fermati: hai fallito, ALTRIMENTI

5a. Considera tale nodo come nodo corrente

5b. Ritorna al passo 1

Dal punto di vista computazionale, lo hill climbing è essenzialmente una procedura di ricerca in profondità nella quale viene espanso non il nodo più recente ma il nodo che sembra più compromettente all'euristica considerata. Più precisamente, una volta espanso un nodo, si calcola la funzione euristica per tutti i suoi figli e si scegli per l'espansione il figlio con il valore minore. Se l'euristica è intesa come il calcolare la distanza che separa il nodo dato da un nodo finale, il nodo migliore sarà quello con il valore più basso; viceversa, se l'euristica calcola la somiglianza fra il nodo dato ed il nodo finale, sarà il migliore quel nodo per il quale il valore della funzione euristica risulta più elevato.

Tale procedura presenta però diversi punti deboli. Diremo che la procedura fallisce in presenza di:

vette secondarie (foothills)

altipiani (plateaus)

creste(ridges)

Le vette secondarie ci portano il problema dei cosiddetti massimi locali. Un massimo locale è uno stato che, pur senza essere finale, risulta migliore di tutti i suoi successori.

In tal caso la procedura si fissa su un valore sub-ottimale senza riuscire a raggiungere la vetta in quanto dovrebbe discendere la cima in considerazione per poi risalire un'altra volta, ma un tale comportamento va al di là delle capacità della procedura.

Nel caso degli altopiani ci troviamo di fronte ad un serie di stati che hanno tutti lo stesso valore euristico. In tal caso la procedura prosegue alla cieca non riuscendo a determinare in quale direzione sia più conveniente far proseguire la ricerca.

Il problema della cresta è ancora più sottile. Supponiamo di procedere lungo un costone di montagna che salga verso la vetta andando da sud-ovest verso nord-est. Il punto nel quale ci troviamo ci permette di spostarci in sole quattro direzioni corrispondenti ai quattro punti cardinali. Comunque ci muoviamo, ci ritroveremo in un punto che è inferiore a quello di partenza facendo in tal modo fallire la ricerca. La procedura di hill climbing "puro" da noi presa in esame implementa una strategia irrevocabile: una volta scelto un nodo da espandere viene cancellato qualsiasi agli altri nodi. Questa versione dell'algoritmo soffre di un ulteriore difetto che potremmo chiamare "cratere vulcanico" che consiste nel fatto che esso potrebbe non terminare in quanto se applicato ad un vulcano ci farebbe arrivare sino al bordo del cratere e poi continuerebbe a farci girare in tondo. Tale difetto può essere facilmente risolto dotando l'algoritmo di un meccanismo di detenzione dei cicli. .

Vediamo l'algoritmo sul seguente esempio.

ESEMPIO 12

4

3

2

1

Successo

1 2 3 4

4

3

2

1

Fallimento

1 2 3 4

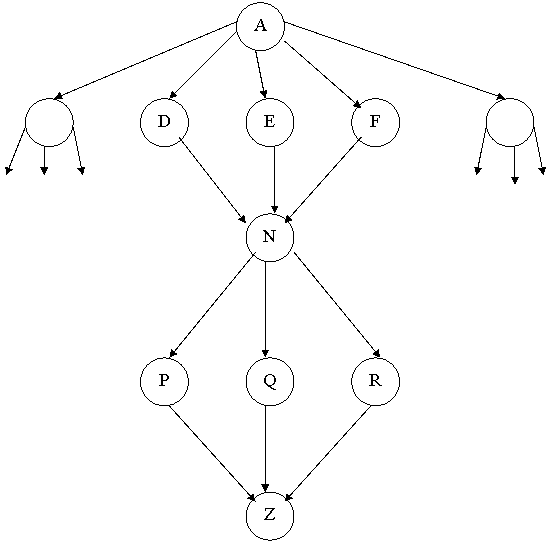
Il compito consiste nell'andare da A a Z. La scelta dei nodi da espandere viene presa in base ad un'euristica che misura la distanza del nodo con quello finale la cui formula, preso il nodo n, è:

f(n) = (coordinata x di Z - coordinata x di n) +(coordinata y di Z - coordinata y di n).

Nell'esempio sopra nel primo caso si parte da A poi si arriva ad E, da qui si sceglie C, poi D e poi Z. Tale cammino risulta essere proprio quello più breve che congiunge A a Z.

Nel secondo caso si parte da A, si arriva in C e poi si sceglie B da cui si può proseguire per D, con f(D)=3, per F, con f(F)=3, e per C, con f(C)=4. In ogni caso bisogna andare in un punto che è più distante dalla Z rispetto al punto in cui ci troviamo visto che f(B)=2. Questo rappresenta un caso di massimo locale in cui l'euristica fallisce.

In definitiva , lo hill climbing è una strategia utile molto buona solo qualora si disponga di una funzione euristica molto buona in grado di evitare vette secondarie, altipiani e creste ed in grado di portarci rapidamente verso l'obiettivo finale.

Best-first

Nella procedura di hill climbing se ci sono vette, altipiani e creste la ricerca non può più procedere (o procede lentamente, alla meno peggio). Per superare queste difficoltà è stata sviluppata un'altra tecnica di ricerca euristica, nota come best-first.

Mentre nella procedura di hill climbing si va avanti nello spazio di ricerca scegliendo il nodo che sembra più promettente su base logica, la ricerca best-first prende in considerazione tutti i nodi che sono stati esaminati sino a quel momento ed espande il nodo che sembra più promettente. Lo hill climbing ha un comportamento paragonabile alla ricerca in profondità mentre la ricerca best-first assomiglia alla ricerca per ampiezza. La differenza sostanziale tra le due procedure sta nel fatto che, mentre la ricerca per ampiezza scegli per l'espansione il cammino più corto (quello che ha minor livello ed è pertanto più vicino alla radice), la ricerca best-first sceglie per l'espansione il cammino che sembra il migliore in relazione alle valutazioni fornite dalla funzione euristica.

ALGORIMO 8

Accerta che le due liste aperti e chiusi siano vuote

Inserisci il nodo radice nella lista aperti

SE non ci sono più nodi nella lista aperti

ALLORA fermati: la procedura ha fallito.

SE il nodo all'inizio di aperti è un nodo finale

ALLORA fermati: hai risolto il problema.

SE il nodo all'inizio di aperti non ha figli OPPURE

il nodo compare già nella lista chiusi

ALLORA toglilo dalla lista

ALTRIMENTI

4a. espandi tale nodo e calcola il valore della funzione euristica

per tutti i suoi figli.

4b. togli tale nodo da aperti ed inseriscilo nella lista chiusi.

4c. inserisci in aperti i figli di tale nodo.

4d. poni come primo nodo di aperti, il nodo che ha il miglior

valore euristico fra tutti quelli contenuti nella lista.

5. Ritorna al passo 2.

Consideriamo una variante del problema del contadino-capra-cavolo, ed è il cosiddetto problema dei missionari e dei cannibali. Il problema nella sua forma più generale è il seguente: n missionari ed n cannibali vogliono attraversare un fiume per mezzo di una barca che è in grado di portare solo k persone (con k < 2*n ).

La difficoltà del problema consiste nel fatto che è necessario impedire che i cannibali mangino i missionari. Per evitare questo increscioso esempio, i missionari che si trovano in ogni istante sulla riva sinistra, sulla riva destra e sulla barca devono essere sempre in numero almeno pari a quello dei cannibali. Con k=1 il problema è insolubile.

Con n=2 e k=2 esso è semplicissimo. Stabiliamo di risolvere la versione nella quale ci siano cinque missionari e cannibali con una barca capace di trasportare tre persone.

Ogni stato problemico è rappresentato da una tripla di numeri indicanti rispettivamente il numero di missionari che stanno sulla sinistra, il numero di cannibali che stanno sulla stessa riva e la posizione della barca (stabilendo convenzionalmente che 1 rappresenti la riva sinistra e 0 la riva destra ). In base a questa convinzione, lo stato iniziale sarà rappresentato dalla terna <5,5,1> e lo stato finale dalla terna <0,0,0>.Quali operatori sono gli operatori del nostro problema? Apparentemente ci servono 16 operatori: occorre infatti prendere in considerazione che sulla barca salgano 1, 2 o 3 cannibali, 1 missionario ed 1 cannibale, 2 missionari ed 1 cannibale, per ciascuna di queste otto possibilità, che la barca vada spostata dalla riva sinistra alla riva destra o dalla riva destra alla riva sinistra. Fortunatamente non tutti gli operatori sono applicabili a tutti gli stati, per cui lo spazio problemico resta ragionevole. Vediamo quale funzione è possibile adottare per guidare la ricerca. Un'idea potrebbe essere quella di considerare una stato più promettente quanto minore è il numero delle persone che devono essere trasportate sulla riva destra. A parità di numero di persone da trasportare, possiamo considerare migliore lo stato che ha la barca sulla parte sinistra del fiume. Tale euristica viene tradotta in una funzione che calcola il valore di uno stato sommando i missionari ed i cannibali che stanno sulla riva sinistra e sottraendo da tale numero il doppio del valore di posizione della barca. Dal momento che una persona deve serve sempre e comunque per remare, avere la barca a sinistra piuttosto che a destra permette di spostare immediatamente sulla riva voluta due passeggeri.

ESEMPIO 15

Esempio dell'algoritmo Best-First applicato al problema dei cannibali e missionari con parametri n=5 e k=3 e funzione euristica f(n)=M+C-2B. Lo spazio di ricerca esaminato è riportato nella figura.

<5,5,1>

<5,4,0> <5,3,0> <5,2,0> <4,4,0>

[9] [8] [7] [8]

<5,4,1> <5,3,1>

[7] [6]

<3,3,0> <5,1,0> <5,0,0>

[8] [6] [5]

<5,2,1> <5,1,1>

[5] [4]

<2,2,0>

[4]

<3,3,1>

[4]

<0,3,0>

[3]

<0,4,1> <0,5,1>

[2] [3]

<0,1,0> <0,2,0>

[1] [2]

<1,1,1> <0,2,1> <0,3,1>

[0] [0] [1]

<0,0,0>

Dallo stato iniziale si possono raggiungere quattro differenti stati applicando gli operatori:

a. 1 cannibale sale sulla barca e va sulla riva destra (<5,4,0>, valore

euristico 9=5+4-2*0).

b. 2 cannibali vanno sulla riva destra (<5,3,0>, valore euristico 8)

c. 3 cannibali vanno sulla riva destra (<5,2,0>, valore euristico 7).

d. 1 missionario e 1 cannibale vanno sulla riva destra (<4,4,0>, valore euristico 8).

Per l'espansione viene scelto lo stato che ha miglior valore euristico cioè quello che vede tre cannibali con la barca sulla riva destra e tutti gli altri sulla riva sinistra. A questo punto gli unici operatori che si possono applicare sono:

a.   1 cannibale ritorna indietro (<5,3,1>, valore euristico 6=5+3-2*1).

b.  2 cannibali tornano indietro (<5,4,1>, valore euristico 7).

Chiaramente non possono tornare tutti e tre altrimenti saremmo allo stato di partenza.

Scegliamo ora il nodo da espandere che è quello con miglior valore euristico tra tutti i nodi potenzialmente espandibili:

<5,4,0>, valore euristico 9

<5,3,0>, valore euristico 8

<5,4,1>, valore euristico 7

<5,3,1>, valore euristico 6

<4,4,0>, valore euristico 8.

Il nodo più promettente tra i percorsi aperti è <5,3,1>, che ha tre figli, il migliore dei quali è <5,0,0> con valore euristico 5 che è migliore rispetto a tutti gli altri sui percorsi aperti.

Questo dà origine a due figli uno dei quali (<5,1,1>) porta ad uno stato precedente e quindi ad un ciclo; si preferisce per cui espandere il fratello (<5,2,1>) che ha valore euristico 5.

Il processo procede in questo modo e, in una decina di passi, raggiunge lo stato finale, identificato dalla terna <0,0,0>.

E' possibile migliorare le funzioni euristiche da utilizzare con l'algoritmo di ricerca best-first in modo che la soluzione che viene trovata non sia solo una soluzione accettabile ma la soluzione ottima. Dato un certo nodo n di uno spazio problemico, sia c(n) il costo del cammino di soluzione ottima passante per n, vale a dire il minimo fra tutti i costi di tutti i cammini che congiungono il nodo iniziale con uno finale e che passano per n. Supponiamo che esistano diversi cammino che passano per il nostro nodo. Con c(n) indichiamo il costo del cammino di soluzione che è ottimo non in assoluto, ma ottimo limitatamente a quelli che passano per n. potrebbe anche darsi che n sia fuori da tutti i percorsi che congiungono la radice con un nodo finale. In tal caso stabiliamo ,per convenzione, che c(n) sia infinitamente grande.

E' evidente come il valore di c(n) derivi dalla somma di due distinte componenti: p(n) che è il costo del cammino ottimo dalla radice ad n (il miglior cammino prima di n ), e d(n) vale a dire il costo del cammino ottimo da n ad un nodo finale (il miglior cammino dopo di n ). In altri termini :

c(n)=p(n)+d(n)

Supponiamo, ancora per un istante, di conoscere il costo di c(n) per tutti i nodi del nostro spazio problemico. Se questo fosse vero, avremmo a disposizione un metodo infallibile per trovare il cammino di soluzione ottimo in assoluto. Posto di avere nel nostro spazio di ricerca h nodi ancora espandibili n₁, n₂, .., n_h, per essere sicuri di ottenere la soluzione ottima basterebbe scegliere per l'espansione il nodo corrispondente a min c( n_i ) con i=1..h, vale adire il nodo al quale è associato il cammino di costo minimo. Vediamo un esempio.

ESEMPIO 16

Nel grafo sono rappresentati 9 diversi modi per andare dal nodo iniziale A al nodo finale Z passando per il nodo intermedio N; esistono cioè nove diversi cammini di soluzione che passano per N .

Ognuno di tali cammini ha un costo che supponiamo noto e che, ovviamente, si ottiene sommando i costi dei diversi operatori. Conoscendo i costi di tutti i cammini di soluzione che passano per N , possiamo calcolare c(N), vale a dire il costo del cammino ottimo passante per N . Tale costo si divide in due diverse componenti : il costo del cammino minimo prima di N e il costo del cammino minimo dopo di N . Per quanto riguarda il cammino minimo prima di N esso e' formato dai nodi A-D-N con P(N)=6. Gli altri due cammini possibili infatti (vale a dire A-E-N e A-F-N ) hanno costi che sono superiori. Come si ricava facilmente dalla figura, il cammino minimo dopo di N e' formato dai nodi N-R-Z con d(n)=5. Il cammino di soluzione di costo minimo e' costituito dunque da A-D-N-R-Z, con c(N)=p(n) + d(n) = 6+5 = 11.

4 5 3

2 3 4

...... ........

3 4 2

....... .......

6 2 3

permette di determinare il costo del cammino di soluzione ottima solo nel caso dei cammini passanti per N. Il cammino ottimo che passa per N passa anche per D. Potrebbe infatti esiste un diverso cammino passante per D e congiungere A con Z di costo inferiore a 11. In definitiva, per poter applicare la ricerca best-first con c(n) come criterio di scelta dei nodi da espandere, sarebbe necessario conoscere i costi di tutti i nodi che compaiono nello spazio problemico, ipotesi surreale nel caso di problemi di una certa complessità.

La secondo cosa da far notare è che c(n) non è ingenerale noto, cercheremo di darne una stima approssimata ed useremo tale stima per guidare la ricerca. Il nostro algoritmo invece di usare il costo reale del cammino ottimo passante per un nodo n userà un costo presunto c¹ (n). Anche tale costo sarà costituito da due componenti ;

c¹(n )=p¹(n)+d¹(n)

rappresentanti rispettivamente il costo presunto del cammino ottimo dalla radice ad n ed il costo presunto da n ad un nodo finale. Il punto critico consiste ovviamente nello stabilire quanto valgono p¹(n) e d¹(n). Ogni volta che, nella ricerca del cammino di soluzione, ci imbattiamo in un nodo n ci troviamo di fronte alla seguente situazione. Di sicuro abbiamo già trovato un cammino che collega un nodo iniziale con n, ma non è detto che tale cammino sia il cammino ottimo, in quanto potrebbe esistere un altro percorso, a noi ignoto, che ci pota dalla radice ad n a costi inferiori. In mancanza di meglio, possiamo usare il costo del cammino effettivamente percorso come stima del cammino di costo minimo dalla radice ad n. Come primo termine p¹(n) della somma adotteremo il costo del cammino da noi percorso fino a n. L'altro termine d¹(n) è più problematico, dal momento che lo spazio da n al nodo finale non è stato ancora esplorato. Pertanto d¹(n) è una reale stima euristica basata sullo conoscenza del particolare dominio problemico. Una procedura best-first che usi l'equazione sopra riportata come funzione euristica prende il nome di algoritmo A.

ALGORITMO 9

Accertati che le due liste aperti e chiusi siano vuote.

Inserisci il nodo radice nella lista aperti assumendo come valore euristico di c' (radice) il valore d' (radice).

SE non ci sono più nodi nella lista aperti

ALLORA fermati: la procedura ha fallito.

SE il nodo all'inizio de aperti è un nodo finale

ALLORA fermati: hai risolto il problema

SE il nodo all'inizio di aperti non ha figli OPPURE il nodo compare già nella lista chiusi

ALLORA toglilo dalla lista,

ALTRIMENTI

4a.   Espandi tale nodo e calcola il valore della funzione c n_i) per tutti i figli di tale nodo utilizziamo come valore di p n_i) il costo del cammino dalla radice e come valore di d n_i) il valore assegnato ai nodi figli della funzione euristica.

4b.   Togli tale nodo da aperti e inseriscilo nella lista chiusi.

4c.   Inserisci in aperti i figli di tale nodo.

4d.   Poni come primo nodo di aperti, il nodo che ha il miglior valore euristico c n) fra tutti quelli contenuti nella lista.

Ritorna al passo 2

Nell'esempio accanto ad ogni nodo n viene riportato il valore stimato d¹(n). L'algoritmo somma tale valore al costo del cammino dalla radice a n al fine di calcolare c¹(n ).

ESEMPIO 17

Inizialmente, il costo stimato dalla radice A al nodo finale si identifica d'(A)=10. Espandendo la radice si ottengono i tre nodi D, E ed F. Il percorso da A a D ha un costo pari a 4 che, sommato ad un costo stimato del cammino da D al nodo finale uguale a 6, dà un valore di c'(D)=4+6=10. Con un ragionamento analogo si trova che c'(E)=16 e che c'(f)=13. Viene scelto per l'espansione il nodo D e si arriva ad N con un ulteriore passo di costo 2. Il cammino da A a P ha un costo pari a 6+3=9 che, aggiunto ad un costo stimato d'(P)=3, porta il costo stimato c'(P)=9+3=12.

Il costo c'(Q), dal momento che il cammino da A a Q ha un costo di 6+4=10 e che il costo del cammino da Q a Z e' stimato uguale a 1, vale 10+1=11. Per quanto riguarda il nodo R, infine, p'(R)=8 e d'(R)=5 da cui c'(R)=8+5=13. Il nodo con il miglior valore euristico e' pertanto Q che viene espanso e porta al raggiungimento del nodo finale Z.

L' algoritmo A ha trovato una soluzione ma non la soluzione di costo minimo. Il cammino A-D-N-Q-Z ha infatti un costo complessivo di 12 mentre il cammino passante per R (cioè A-D-N-R-Z) ha un costo di 11 inferiore al precedente.

5 3

[6] [11] [10]

....... 2 3 4 ........

4 2

.......

[3] [1] [5]

6 2 3

[0]

Un algoritmo A che usi una funzione euristica d¹(n) la quale fornisce una stima ottimistica del costo necessario a raggiungere la soluzione, una funzione cioè tal che

d¹(n_i) <= d (n_i)

per tutti gli i nodi dello spazio problemico viene detto algoritmo A* che gode di una serie di proprietà matematiche. Menzioneremo solo la più importante fra queste che afferma che l'algoritmo A* è ammissibile. Un algoritmo è detto ammissibile se esso produce la soluzione ottima, posto che tale condizione esista. Non conoscendo il vero valore d(n) il costo reale necessario a raggiungere la soluzione da un dato nodo, e dovendo darne una valutazione stimata, tutto quello che dobbiamo fare è usare una stima ottimistica ed in tal caso abbiamo la garanzia di trovare la miglior soluzione per il nostro problema. Assumendo che d¹(n) =0 per tutti i nodi l'ammissibilità è comunque rispettata ma tale funzione non ci fornisce alcuna guida per la ricerca. Se l'algoritmo A* usasse d¹(n) =0 si comporterebbe in modo molto simile ad una procedura di ricerca per ampiezza, e coinciderebbe con essa se a tutti gli archi venisse assegnato un costo unitario. In tal caso avremo dunque una ricerca altamente inefficiente.

Introduciamo il concetto di informatività di un'euristica utilizzata da un algoritmo A* . Supponiamo di avere due funzioni euristiche entrambe ottimiste di cui però una più ottimista dell'altra. Supponiamo cioè di avere due funzioni d¹₁(n) e d¹₂(n) tali che:

d¹₁(n_i) <= d¹₂(n_i) <=d(n_i)

per tutti gli i nodi dello spazio problemico. In tal caso si dice che d¹₂ è un'euristica più informata di d¹₁. Se un'euristica d¹₂ è più informata rispetto ad un'euristica d¹₁ allora essa genera uno spazio di ricerca che è un sottoinsieme dello spazio di ricerca generato da d¹₁.

Ritornando alle euristiche impiegate nel gioco del lotto, si comprende facilmente come l'euristica f'' che usa la distanza di Manhattan risulti più informata rispetto all'euristica f' che calcola semplicemente il numero di tesse fuori posto. Il valore che f'' assegna ad un nodo infatti non potrà mai essere inferiore a quello assegnato da f' dal momento che ogni tessera fuori posto avrà bisogno di almeno uno spostamento per raggiungere la posizione finale. Questo non significa che il tempo per trovare la soluzione sarà sicuramente inferiore, in quanto essendo più complicata la distanza di Manhattan richiederà ogni volta, per poter essere calcolata, un tempo superiore a quello necessario a contare le tessere fuori posto. Il tempo del calcolo della funzione andrà ad incidere sul tempo necessario per trovare la soluzione.

Concludendo il tempo richiesto per risolvere un problema deriva dalla somma di due componenti:

il tempo speso nel decidere come risolvere il problema (tempo di calcolo della funzione euristica ) ed

il tempo speso nel risolverlo effettivamente (tempo di ricerca).

Ricerca euristica in alberi AND/OR

Le funzioni euristiche possono venir usate nell'esplorare spazi di ricerca rappresentati mediante alberi AND/OR anche se, in questo caso, non è pensabile di poter applicare direttamente gli algoritmi usati per la ricerca nello spazio degli stati. Vediamo il perché.

Cominciamo ad introdurre il concetto di costo di una soluzione in un albero AND/OR. Nel caso di problemi rappresentati mediante grafi AND/OR la soluzione è costituita da un sottoalbero e non da un cammino, e non è immediatamente chiaro come si possa calcolarne il costo. Il fatto è che il costo è un concetto difficilmente associabile agli operatori di scomposizione. Può essere invece attribuire un costo ai nodi rappresentanti problemi primitivi: intuitivamente il costo di un tale nodo rappresenta la difficoltà del problema o, se si preferisce, costituisce una misura delle risorse (tempo, denaro, ecc. ) che è necessario impiegare per poterlo risolvere. Partendo da tali costi è possibile calcolare i costi di tutti i nodi del grafo propagando verso l'alto i costi dei nodi foglia. Il costo della soluzione di un problema così concettualizzato verrebbe a coincidere con il costo del nodo radice.

La propagazione dei costi dei nodi di un albero AND/OR avviene in base ai seguenti criteri. Per ogni nodo n :

se n è un problema primitivo, il suo costo è rappresentato dal costo del problema;

se n è un nodo foglia irrisolvibile, il suo costo viene considerato come infinito;

se n è un nodo OR allora si considera come suo costo il minimo fra i costi dei suoi figli;

se n è un nodo AND, allora si considera come suo costo la somma dei costi dei suoi figli.

ESEMPIO 13

Vediamo come i criteri di propagazione sono applicati al problema rappresentato dall'albero in figura:

1 2

6

3 4

Inizialmente si conoscono solo i costi dei nodi foglia: D(1), H(6), M(3), N(4), G(2), L (problema irrisolvibile).

Il costo del nodo E è pari a quello del suo unico figlio H, il costo del nodo B è la somma dei costi dei suoi figli D ed E, essendo un nodo AND (1+6=7).

Anche I è un nodo AND e quindi ha costo 7 (3+4); il nodo F invece, essendo un nodo OR, ha come costo il minimo dei costi dei suoi figli e quindi 7 (min (7,

A questo punto è possibile calcolare il costo del nodo C che ha per figli F e G, essendo C un nodo AND, questo valore sarà dato dalla somma dei costi dei suoi figli (9=7+2).

Il problema A ha dunque due soluzioni: la prima è rappresentata dal sottoalbero radicato in B (di costo 7), la seconda da quello radicato in C (di costo 9).

Essendo la radice del problema un nodo OR, il costo della soluzione del problema è il minimo fra i costi delle due soluzioni cioè 7.

Mentre l'algoritmo A* prende in esame per l'espansione il nodo più promettente, nel caso di ricerca in un albero AND/OR si ha bisogno di identificare il sottoalbero di soluzione più promettente. In definitiva a mano a mano che si espande un sottoalbero e si acquisiscono nuove informazioni , i valori euristici assegnati ai nuovi sottoproblemi portano ad un ricalcolo dei costi di soluzione. In ogni istante la ricerca procede espandendo il sottoalbero che, in quel momento, sembra più promettente.

Un algoritmo che funzioni in questo modo, attuando una ricerca best-first in un albero AND/OR utilizzante delle stime euristiche sulle difficoltà dei diversi nodi, viene detto algoritmo A()*.