TEORIA DEI FUZZY SETS

Se consideriamo, per esempio, l'insieme

X= ed il suo sottoinsieme A=, possiamo definire per ogni abitante della città considerata, in base al sesso la sua appartenenza all'insieme A che abbiamo definito.

Formalmente definiamo una funzione di appartenenza m_A(x) tale che

m_A(x) = 1 sse x è uomo

m_A(x) = 0 sse x è donna

Ci sono, però, dei casi in cui la teoria classica non riesce a classificare in maniera adeguata gli elementi di un sottoinsieme dell'universo del discorso. Ad esempio, consideriamo l'universo X che racchiude la popolazione di una città e consideriamone il sottoinsieme che include le persone di statura alta.

Volendo applicare la teoria classica degli insiemi, supponiamo di porre un limite per il quale si possa dire che tutte le persone al di sopra di 1.70 m. possono considerarsi alte. Questo tipo di posizione, però, non descrive compiutamente l'insieme delle persone alte di una città, poichè è evidente che le persone di 1.70 m non sono più alte di quelle di 1.69 m in maniera così netta da poter dire che le prime sono alte, mentre le seconde non lo sono. E la cosa appare ancora più evidente confrontando le persone alte 1.70 m con quelle che sono alte 2.00 m.

Quello che in realtà possiamo dire è che queste tre categorie di persone sono più o meno tutte appartenenti al sottoinsieme "popolazione alta di X", ma con grado differente.

Infatti, le persone alte 1.70 m sono alte solo leggermente più di quelle di 1.69 m, mentre lo sono meno di quelle alte 2.00 m. Volendoci esprimere in maniera diversa: le persone alte 2.00 m appartengono più di quelle di 1.70 m e 1.69 m al sottoinsieme delle persone alte; a cui queste due ultime categorie appartengono in misura pressochè uguale.

Un'idea centrale nella filosofia Platonica è che, nel mondo reale, 353b17d gli elementi sono perturbati da imperfezioni e quindi, per esempio non esiste alcun elemento perfettamente circolare. Le "nozioni perfette" o i "concetti esatti" corrispondono ad un tipo di oggetti tenuti in conto nella matematica pura, mentre le "strutture inesatte" prevalgono nella vita reale. E' convinzione diffusa che le strutture inesatte siano ricche abbastanza di operazioni e proprietà da essere di uso autentico nella costruzione di modelli per un'ampia varietà di situazioni. E' nostro intento introdurre un punto di vista unificante per la nozione di inesattezza, basata sulla teoria dei fuzzy set introdotta da Zadeh nel 1962; in tale articolo viene ipotizzata una "matematica fuzzy" o di quantità turbate che non sono descrivibili in termini di distribuzioni di probabilità. A questo articolo ne seguì un altro nel 1965 ove può trovarsi una esposizione tecnica proprio di una tale matematica definita teoria dei fuzzy sets. Non esiste però un modo unico per costruire una tale teoria, tutti gli approcci di cui tratteremo però includono la teoria degli insiemi ordinari come caso particolare. La teoria dei fuzzy sets di Zadeh, appare come la più intuitiva, sebbene concetti come l'inclusione o l'uguaglianza possono sembrare troppo restrittivi. C'è, inoltre una certa arbitrarietà nella scelta dell'insieme di valutazione per gli elementi: l'intervallo [0,1] è il più comunemente usato, ma sono possibili anche altre scelte tipo quelle che compaiono sotto l'etichetta L-fuzzy sets. Nel 1967 Goguen fornisce le ragioni che sostengono la rappresentazione dei concetti inesatti con i fuzzy sets. L'argomento più convincente è un teorema di rappresentazione che dice che qualsiasi sistema che soddisfa certi assiomi è equivalente ad un sistema di fuzzy sets.

Essenzialmente, la sfuocatezza (fuzziness) è un tipo di imprecisione che deriva da un raggruppamento di elementi in classi che non hanno confini ben definiti. Tali classi, chiamate fuzzy sets, sorgono, per esempio, ogni qualvolta descriviamo l'ambiguità, la vaghezza e l'ambivalenza nei modelli matematici di fenomeni empirici. Poichè certi aspetti della realtà sfuggono sempre da tali modelli, l'approccio strettamente binario (e persino ternario) al trattamento di fenomeni fisici non è sempre adatto per la descrizione di sistemi nel mondo reale e gli attributi delle variabili di sistema spesso emergono da una vaghezza elusiva, da un riadattamento del contesto o da un effetto dell'imprecisione umana. In moti casi, comunque, anche se il modello è preciso, la sfuocatezza può essere una concomitante della complessità.

La teoria dei fuzzy sets ha tra i suoi scopi lo sviluppo di una metodologia per la formulazione e la soluzione di problemi che sono troppo complesi o troppo mal definiti da essere suscettibili di un'analisi da parte di tecniche convenzionali.

La teoria dei fuzzy sets si occupa di un sottoinsieme A dell'universo del discorso X dove la transizione tra la piena appartenenza e la non appartenenza è graduale piuttosto che improvvisa.

Volendo esprimere formalmente questo concetto dobbiamo modificare la funzione di appartenenza vista precedentemente. Con la nuova funzione caratteristica non dovremo indicare più la semplice appartenenza, ma il grado di appartenenza. quindi questa funzione non assumerà più i semplici valori , ma un valore compreso nell'intervallo [0,1] dei reali con la convenzione che la funzione caratteristica sia crescente cioè l'appartenenza massima avrà grado 1.

La nuova funzione caratteristica avrà la forma

m_A(x) = y

Volendo esemplificare, consideriamo tre persone della città descritta dall'universo X. Supponiamo che l'altezza della prima persona sia quella di 1.69 m, quella della seconda 1.70 m, quella della terza 2.00 m.

Una possibile assegnazione di valori per queste tre persone potrebbe essere

m_A(prima persona) = 0.49

m_A(seconda persna) = 0.50

m_A(terza persona) = 0.85

Facciamo notare come non vi sia nessuna relazione di tipo numerico tra i valori assunti dalla funzione di appartenenza ed il valore che misura in metri le altezze reali delle persone. Questo perchè noi con la funzione di appartenenza indichiamo solo il grado di appartenenza stesso al sottoinsieme.

E' anche vero che questi valori sono del tutto arbitrari, e potrebbero essere ridefiniti con qualsiasi altra terna di valori che rispetti le relazioni esistenti tra gli elementi x dell'universo X. Inoltre il concetto espresso include anche la definizione classica di appartenenza ad un insieme. Fin qui il concetto alla base della teoria fuzzy.

A causa della sua generalizzazione tale teoria ha uno scopo più ampio di applicabilità della teoria astratta degli insiemi nella risoluzione di problemi che comportano in qualche modo una valutazione soggettiva. Intuitivamente, quindi, un fuzzy set è una classe che ammette la possibilità di appartenenza parziale in essa.

Definizione 1.1

Sia X uno spazio di oggetti (universo del discorso) e x un generico elemento di X.

Un "fuzzy set" A in X è caratterizzato da una "funzione di appartenenza" m_A(x):

m_A: x X ----> m_A(x) [0,1] incluso in R

dove m_A(x) è detto grado di appartenenza di x in A

In parole più il valore di m_A(x) si avvicina ad 1 più x appartiene ad A.

Se A è un insieme ordinario la m_A si riduce alla nota "funzione di appartenenza":

m_A: x X ----> m_A(x)

m_A(x)=1 sse x A

m_A(x) sse x A

Notiamo che, per i fuzzy sets viene a mancare il significato di confine risultando non ben definito.

Il fuzzy set A è completamente caratterizzato dall'insieme delle coppie

A = [(x, m_A(x)), x X]

In questo contesto preferiamo però utilizzare la seguente notazione proposta da Zadeh:

Supponiamo che l'insieme finito X= sia espresso come X= x +x +...+x_n con l'accordo che questa è la rappresentazione di X come unione dei "singletons" che lo costituiscono, dove il segno + gioca il ruolo di "unione" piuttosto che di somma aritmetica.

(Nota: x_j+x_k=x_k+x_j e x_j+x_j=x_j per j,k=1,2,...,n)

Come semplice estensione di questa notazione un fuzzy set A su X, se X è un insieme finito , sarà espresso come:

A = m_A(x )/x m_A(x )/x m_A(x_n)/x_n

Se X non è finito:

A = _X m_A(x)/x

(I simboli e + non vanno intesi in senso matematico, ma in quello di unione insiemistica)

E' importante notare che l'insieme X, considerato come universo, non è un insieme fuzzy.

I gradi di appartenenza denotano un ordinamento degli oggetti nell'universo; è interessante notare che il valore di grado di appartenenza m_A(x) di un oggetto x in A può essere interpretato come il grado di compatibilità del predicato associato ad A ed all'oggetto x.

In generale distinguiamo tre tipi di inesattezza:

-Generalità, che è un concetto che si applica ad una varietà di situazioni,

-Ambiguità, che descrive più di un sottoconcetto distinguibile,

-Vaghezza, se non sono definiti limiti precisi.

Tutti e tre i tipi di inesattezza sono rappresentati da un fuzzy set.

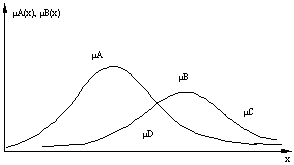
La "generalità" occorre quando l'universo non è solo un punto, l'ambiguità si presenta quando c'è più di un massimo locale di una funzione di appartenenza e la vaghezza occorre quando la funzione assume valori diversi da 0 e 1.

Esempio 1.1

X insieme delle monete metalliche in corso in Italia

X =

Su tale universo siano A e B due insiemi fuzzy rispettivamente delle "monete grandi" e delle "monete di valore".

Secondo la rappresentazione di Zadeh si ha:

A=grandezza=0.8/100L.+0.5/200L.+0.4/50L.+0.4/500L.+0.1/10L.

B=valore=0.2/100L.+0.4/200L.+0.1/50L.+ 0.8/500L.+ 0.02/10L.

Esempio 1.2

Consideriamo la classe di tutti i numeri reali che sono molto più grandi di 1.

Possiamo rappresentare tale insieme come:

A=.

Esso non è un insieme ben definito per le ragioni menzionate prima. Questo insieme può essere definito soggettivamente da una funzione di appartenenza così fatta:

m_A(x)=0 se x≤1 (1)

m_A(x)=(x-1)/x se x>1

L'assegnamento di una funzione di appartenenza di un fuzzy set è soggettiva in natura, in generale, riflette il concetto in cui il problema è visto. Sebbene tale assegnamento sia "soggettivo" esso non può avvenire arbitrariamente. Per esempio, sarebbe sbagliato assegnare la funzione di appartenenza dell'esempio come:

m_A(x)=(x-1)/x se x≤1

m_A(x)=0   se x>1

Funzioni come quest'ultima saranno chiamate funzioni non ammissibili del fuzzy set A. Funzioni, invece come la (1) ed altre quali:

m_A(x)=0   se x≤1

m_A(x)=1-exp(-0.1(x-1)) se x>1

che soddisfano la condizione 0≤m_A(x)≤1 per tutte le x, e sono consistenti con la specifica dell'insieme, saranno chiamate "funzioni ammissibili" di A.

2. ALCUNI TERMINI DI NOMENCLATURA.

Il Supporto (o Sostegno) di un insieme fuzzy A è l'insieme ordinario, sottoinsieme di X, tale che i suoi elementi hanno un valore di appartenenza positivo:

suppA =

I Punti di Incrocio (o punti di attraversamento) sono gli elementi x dell'universo X il cui grado di appartenenza in A sia pari a 0.5.

L'Altezza (o il peso) di A è definita come il valore di appartenenza più alto degli elementi di X:

hgt(A) = sup _{x X} m_A(x) (estremo superiore di m_A(x))

Un insieme fuzzy A si dice Normalizzato se e solo se esiste un elemento dell'universo che ha grado di appartenenza pari ad 1. Questa definizione implica hgt(A)=1.

Possiamo anche dire che se sup_X m_A(x) = 1 l'insieme fuzzy A è chiamato normale.

Un insieme fuzzy A non vuoto può sempre essere normalizzato dividendo m_A(x) per sup_X m_A(x).

Esempio 2.1

Sia l'universo l'intervallo [0,120], essendo x l'età di un individuo. Un sottoinsieme fuzzy A di X etichettato "vecchio" può essere definito da una funzione di appartenenza come:

m_A(x)=0 se 0≤x≤40

m_A(x)=[1+(x-40/5)^-2]^-1 se 40<x≤120

In questo esempio il supporto di "vecchio" è l'intervallo (40,120], il peso di "vecchio" è effettivamente 1 ed il punto d'incrocio di "vecchio" è 45.

Esempio 2.2

X = N =

Sia A = 0.1/7 + 0.5/8 + 0.8/9 + 1.0/10 + 0.8/11 + 0.5/12 + 0.1/13

A è un fuzzy set di interi approssimativamente uguale a 10.

Esempio 2.3

X = R =

m_A(x) = 1/ (1+[1/5(x-10)]²)

cioè A = _R 1/ (1+[1/5(x-10)]²) / x

A è un fuzzy set di numeri reali raccolti intorno a 10.

L'insieme fuzzy vuoto è l'insieme per cui ogni elemento dell'universo X ha valore di appartenenza nullo:

A = <==> m_A(x) = 0 "x X

Due fuzzy sets A e B sono detti essere uguali se e solo se

_X m_A(x)/x= _X m_B(x)/x

oppure

m_A(x) = m_B(x) "x X

Definiamo infine l'inclusione di due fuzzy sets come:

A contenuto in B <==> m_A(x) ≤ m_B(x)

ovvero _X m_A(x)/x ≤ _X m_B(x)/x.

Si noti che il ≤ è dato qui in senso booleano.

3. INTERSEZIONE ED UNIONE DI FUZZY SETS.

L'unione e l'intersezione classica può essere estesa ad insiemi fuzzy attraverso formule proposte da Zadeh.

Siano A e B fuzzy sets su X, m_A m_B funzioni di appartenenza di A e B.

Il fuzzy set unione di A e B è un fuzzy set C=A B la cui funzione di appartenenza è relazionata a quelle di A e B da:

m_C(x) = max ( m_A(x) , m_B(x) ) x X

ovvero A B è _X m_A(x) m_B(x)) /x dove è il sibolo di max.

L'operazione binaria gode della proprietà associativa.

L'unione si può definire equivalentemente come "il più piccolo fuzzy set che contiene A e B"

Il fuzzy set intersezione di A e B è un fuzzy set D=A B la cui funzione di appartenenza è:

m_D(x) = min ( m_A(x) ,m_B(x) ) x X

ovvero A B è _X m_A(x) m_B(x)) /x dove è il sibolo di min

L'intersezione tra A e B è il più grande fuzzy set contenuto sia in A che in B.

L'operazione binaria è associativa.

Notiamo che queste formule danno l'unione e l'intersezione ordinarie quando l'insieme di valutazione è ridotto a . Ovviamente ci sono altre possibili estensioni dell'unione e dell'intersezione.

Esempio 3.1

Partendo dall'Esempio 1.1.

A = monete grandi B = monete di valore

C = A B = monete grandi o di valore

D = A B = monete grandi e di valore

C = 0.8/100L. + 0.5/200L. + 0.4/50L. + 0.8/500L. + 0.1/10L.

D = 0.2/100L. +0.4/200L. +0.1/50L. + 0.4/500L. + 0.02/10L.

La scelta degli operatori max e min per definire le due operazioni esposte precedentemente è giustificata da Bellman e Giertz.[1973].

Gli operatori min e max non sono i soli che potrebbero essere stati scelti a modellare l'intersezione o l'unione degli insiemi fuzzy. Sorge una domanda,perchè questi e non altri?

Bellman e Gertz indirizzarono questa questione nel 1973 assiomaticamente. Essi mostrarono da un punto logico, che interpretando l'intersezione come "AND logico", l'unione come "OR logico", e l'insieme fuzzy A come l'affermazione "l'elemento x appartiene all'insieme A" può essere accettato come più o meno vera. E' molto istruttivo seguire il loro argomento che e' un esempio eccellente per una giustificazione assiomatica di modelli matematici specifici.

Consideriamo S e T per cui i valori di verità sono m_S e m_T, rispettivamente con m_S e m_T appartenenti a [0,1]. Il valore di verità della combinazione di queste istruzioni "AND" e "OR", m_{(S AND T)} e m_{(S 0R T)} entrambe appartenenti all'intervallo [0,1] sono interpretate come i valori delle funzioni di appartenenza dell'unione e dell'intersezione rispettivamente di S e T. Cercheremo due funzioni con valori reali f e g tali che:

m_{S AND T} = f(m_S m_T

m_{S OR T} = g(m_S m_T

Bellman e Giertz sentirono di imporre su f e g le seguenti restrizioni:

i. f e g sono continue in m_S e m_T

ii.f e g sono simmetriche cioè:

f(m_S m_T) = f(m_T m_S

g(m_S m_T) = g(m_T m_S

iii. f(m_S m_S) e g(m_S m_S) sono strettamente crescenti in m_S

iv. f(m_S m_T) ≤ min(m_S m_T) e g(m_S m_T) ≥ max(m_S m_T

v. f(1,1) =1 e g(0,0) =0

vi. Istruzioni equivalenti devono avere valori di verità uguali e:

S AND (S OR S

è equivalente a (S AND S OR (S AND S ) e perciò devono essere vere.

Bellman e Giertz formalizzano il precedente come segue:

Usando i simboli & per "AND" (intersezione) e per "OR"(unione), abbiamo le seguenti sette restrizioni:

m_S & m_T m_T & m_S m_S m_T m_T m_S

m_S & m_T) & m_U m_S &(m_T & m_U), (m_S m_T m_U m_S m_T m_U

m_S &(m_T & m_U m_S & m_T m_S & m_U),

m_S m_T & m_U m_S m_T)&(m_S m_U

m_S & m_T e m_S m_T sono continue e non decrescenti

m_S & m_S e m_S m_S sono strettamente crescenti in m_S

m_S & m_T ≤ min(m_S m_T), m_S m_T ≥ max(m_S m_T

7. 1&1 = 1, 0

inoltre m_S&T = min(m_S m_T) e m_{S T} = max(m_S m_T

Per il complemento si assumerà che se "S" è vera, il suo complemento "NOT S" è falso, oppure se m_S =1 allora m_NOTS=0 e viceversa.

Equivalentemente possiamo dire che max e min sono i soli operatori f e g che hanno i seguenti requisiti:

(i) Il valore di appartenenza di x in un fuzzy set composto dipende dal valore di appartenenza di x nei fuzzy sets elementari che lo formano ma non da altro:

"x X m_C(x) = f ( m_A(x) , m_B(x) )

m_D(x) = g( m_A(x) , m_B(x) )

(ii) f e g sono operatori commutativi, associativi e mutuamente distributivi

(iii) f e g sono continui e non decrescenti rispetto ad ogni uno degli argomenti.

(Intuitivamente, l'appartenenza di x in A B o A B non può decrescere quando l'appartenenza di x in A o B cresce. Un piccolo incremento di m_A(x) o m_B(x) non può indurre un forte incremento di m_C(x) o m_D(x).

(iv) f(u,u) e g(u,u) sono strettamente crescenti.

Se m_A(x m_B(x )> m_A(x m_B(x ), allora l'appartenenza di x in C o D è certamente strettamente maggiore di quella di x

(v) l'appartenenza ad A B richiede di più, e l'appartenenza ad A B meno dell'appartenenza ad A o B:

"x X m_C(x) ≥ max ( m_A(x) , m_B(x) )

m_D(x) ≤ min( m_A(x) , m_B(x) )

(vi) l'appartenenza completa in A e in B implica la completa appartenenza in A B. La mancanza completa di appartenenza in A e B implica la mancanza completa di appartenenza in A B:

g(1,1) = 1 f(0,0) = 0

Le assunzioni riportate sono consistenti e sufficienti ad assicurare l'unicità della scelta degli operatori di unione ed intersezione.

Illustriamo di seguito l'unione e l'intersezione di due fuzzy sets in R

Diamo ora suggestiva interpretazione per l'unione e l'intersezione di fuzzy sets.

Siano A ,...,A_n fuzzy sets e m_Ai x i=1,...,n) le relative funzioni caratteristiche; associamo a m_Ai x un "setaccio" S_i(x) le cui maglie siano di "taglia" m_Ai x

Allora l'unione tra m_Ai x e m_Aj x e l'intersezione corrispondono, rispettivamente a combinazioni in parallelo ed in serie di S_i(x) ed S_j(x):

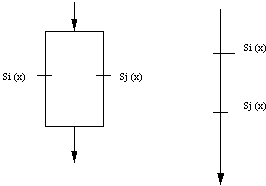
Connessioni in parallelo ed i serie di "setacci" simulanti unione ed intersezione.

In S_i(x) passa tutto quello che è minore o uguale ad m_Ai x mentre in S_j(x) passa tutto quello che è minore o uguale ad m_Aj x

Considerando il caso in cui S_i(x) e S_j(x) connessi in parallelo, abbiamo che i setacci operano in maniera indipendente, quindi in uscita si avrà tutto quello che è minore o uguale del max (m_Ai x m_Aj x ), ossia minore o uguale ad m_{Ai Aj} x

Se invece consideriamo i due setacci connessi in serie, vi è prima un filtraggio tramite S_i(x) e poi ve ne è un altro tramite S_j(x), per cui in uscita si ha solo quello che passa dal filtro più piccolo, cioè tutto quello che è minore o uguale al min (m_Ai x m_Aj x m_{Ai Aj} x

4. CONCETTO DI APPARTENENZA

L'appartenenza relativa ad insiemi ordinari perde di significato applicata a fuzzy set, non ha senso parlare di un punto x appartenente ad A.

Si possono introdurre due livelli a e b

(0 < a < 1, 0 < b < 1, a > b)

e convenire di dire:

x A se m_A x a

x A se m_A x b

x "ha uno stato indeterminato relativo ad A" se b<m_A x)<a

Ciò conduce ad una logica a tre valori con tre valori di verità:

V( m_A x a F( m_A x b I( b<m_A x)<a

5. ALCUNE OPERAZIONI ALGEBRICHE (ALTRI OPERATORI)

Consideriamo dei fuzzy sets ordinari (fuzzy sets di tipo 1) e definiamo alcune operazioni addizionali.

Definizione 5.1

Il prodotto cartesiano di fuzzy set è definito come segue: Siano A ,A ,...,A_n, fuzzy set in X x ...x X_n. Il prodotto cartesiano è quindi un fuzzy set nel prodotto spaziale X x ...x X_n con la funzione di appartenenza

m _{A1 x ...x An)}= min

Definizione 5.2

La potenza m-esima di un fuzzy set A è un fuzzy set con la funzione di appartenenza

(m_R)^m(x) =[m_A(x)]^m, x X

Le operazioni algebriche addizionali sono definite come segue:

Definizione 5.3

La somma algebrica (somma probabilistica) C=A+B è definita cosl

C =

dove

m_A+B(x) = m_A(x) + m_B(x) - m_A(x) . m_B(x)

Definizione 5.4

La somma limitata C = A B è definita così

C =

dove

m_{A B}(x) = min

dove "+ è la somma aritmetica.

Definizione 5.5

La differenza limitata C = AQ B è definita cosl

C =

AQ B è il fuzzy set di elementi che appartengono ad A più che a B.

Definizione 5.6

Il prodotto algebrico di due fuzzy set C=A ° B è definito cosl

C =

Si noti che A°B incluso in A B

Così, A^a dove a è un numero positivo, dovrebbe essere interpretato come:

A^a è _X m_A(x)^a ) /x

Analogamente se a è un numero non negativo tale che

a Sup_x m_A(x) ≤ 1 allora aA è _X a m_A(x) /x

Come caso speciale può essere definito l'operatore di Concentrazione: CON(A) è A², mentre la Dilatazione può essere espressa da DIL(A) è A^0.5.

Esempio 5.1

Siano

A(x) =

B(x) =

Le definizioni suddette sono quindi illustrate dai seguenti risultati :

A x B =

A²=

A + B=

A B=

A Q B=

A ° B=

Per quanto riguarda la differenza simmetrica, nella struttura della teoria dei fuzzy sets ci possono essere modi diversi per definire una differenza simmetrica. Dapprima il fuzzy set A B di elementi che appartengono più ad A che a B o al contrario è definito come

Per ogni x X, m_{A B}(x) = |m_A(x) - m_B(x)|

Tale operazione non è associativa.

In secondo luogo, il fuzzy set ADB degli elementi che approssimativamente appartengono ad A e non a B o al contrario a B e non ad A è definita come

"x X, m_AD­B(x)=max [min(m_A(x), 1- m_B(x)), min(1-m_A (x), m_B(x))]

Si può mostrare che tale operazione è associativa.

Il Quadrato sinistro di A è denotato con ²A ed è definito:

A è _V m_A(x) /x² dove V è

6.COMPLEMENTO DI UN FUZZY SET A.

Il complemento di A, denotato con A' è definito da:

A' è _X m_A(x)) /x

vale a dire m_A (x) =1- m_A (x) " x X.

Esempio 6.1

Con riferimento all'usuale insieme delle monete (Es.1.1), il complemento dell'insieme A sarà A' = monete piccole

A' = 0.2/100L. +0.5/200L. +0.6/50L. + 0.6/500L. + 0.9/10L.

Le condizioni generali da imporre ad una funzione di complementazione h furono proposte da Bellman e Giertz nel 1973.

m_A (x) dipende solo da m_A (x): m_A (x) = h( m_A (x))

-h(0) = 1 e h(1) = 0, per recuperare l'ordinaria complementazione quando A è un sottoinsieme ordinario.

-h è continua e strettamente decrescente monotona, poichè l'appartenenza in A' dovrebbe diventare più piccola quando l'appartenenza in A aumenta.

-h è involutiva: h(h( m_A (x))) = m_A (x)

Le assunzioni di sopra non determinano h univocamente nemmeno se si richiede h(1/2)=1/2

7. INSIEME POTENZA

Sia P(X) l'insieme dei sottoinsiemi fuzzy di X.

Esempio 7.1

Se X è un insieme di oggetti colorati ed A il sottoinsieme di quelli rossi, m_A(x) misura il grado di rosso di x. Un oggetto rosa ha un valore di appartenenza vicino a 1/2 e quindi appartiene ugualmente ad A e A'.

I ricercatori Netto e Chapin propongono una assiomatizzazione della teoria dei fuzzy sets. In un simile approccio i fuzzy sets sono costruiti dall'inizio, senza vederli come una superstruttura di una predeterminata teoria di insiemi ordinari.

La sola relazione primitiva usata nella teoria è una relazione ternaria interpretata come una relazione di appartenenza. Seguono 14 assiomi.

La difficoltà maggiore è mostrare che il suo solo modello è l'universo dei fuzzy sets.

8. OPERATORI ALTERNATIVI SU P(X)

Operatori di tipo probabilistico:

Intersezione

"x X m_A.B(x) = m_A(x) . m_B(x) (prodotto)

Unione

"x X m_A+B(x)=m_A(x) + m_B(x) - m_A(x).m_B(x)

(somma probabilistica)

Sotto questi operatori P(X) risulta essere una struttura non distributiva pseudocomplementata

In particolare + e . soddisfano solo la commutatività, l'associatività, l'identità, le leggi di De Morgan e A.O = O, A + X = X

Usando questi operatori inoltre una modifica di A (o B) non implica necessariamente una alterazione in A B o A B.

L'unione e l'intersezione sono detti in questo caso non interagenti.

9. INSIEMI LIVELLO (a-cuts)

Per meglio esibire un elemento x che appartiene ad A, possiamo richiedere che il suo valore di appartenenza sia più grande di una qualche soglia aÎ(0,1].

L'insieme ordinario di tali elementi è l'insieme livello A_a di A.

A_a

Si definisce anche l'insieme livello forte:

A_a

La funzione di appartenenza di un fuzzy set A può essere espressa in termini delle funzioni caratteristiche dei suoi insiemi livello in accordo con la formula:

m_A(x)=sup_a min[a, m_Aa (x)] a

dove

m_Aa (x) = 1 sse x appartiene ad A_a

=0 altrimenti

Si può facilmente controllare che valgono le seguenti proprietà:

(A B)_a= A_a B_a

(A B)_a A_a B_a

Comunque (A')_a = (A _-a ' ≠ (A_a)' se a a

I risultati derivano dal fatto che generalmente ci sono elementi che non appartengono nè ad A_a nè ad (A')_a, cioè:

(A_a (A')_a ≠ X).

Radecki [1977] ha definito i fuzzy sets livello di un fuzzy set A come i fuzzy sets A_a con aÎ (0,1) tale che:

A_a

La ragionevolezza che stà dietro questa definizione è il fatto che nelle applicazioni pratiche è sufficiente considerare i fuzzy sets solamente definiti in una parte del loro sostegno, la parte più significativa, allo scopo di salvaguardare il tempo di computazione e lo spazio di memoria del calcolatore.

Un fuzzy set A può essere decomposto nei suoi insiemi livello attraverso una espressione del tipo (Principio di risoluzione):

A = a A_a oppure A = S_a a A_a

dove a A_a è il prodotto di uno scalare per un insieme.

Il principio di risoluzione offre come risultato una combinazione di quegli elementi di A che cadono nello stesso insieme livello.

Esempio 9.1

Più specificatamente, si supponga A rappresentato nella seguente forma:

A = 0.1 / 2 + 0.3 / 4 + 0.5 / 7 + 0.9 / 8 + 1 / 9

Allora A può essere riscritto come:

A = 0.1 / 2 + 0.1 / 4 + 0.1 / 7 + 0.1 / 8 + 0.1 / 9

+ 0.3 / 4 + 0.3 / 7 + 0.3 / 8 + 0.3 / 9

+ 0.5 / 7 + 0.5 / 8 + 0.5 / 9

+ 0.9 / 8 + 0.9 / 9

+ 1.0 / 9

o

A = 0.1(1/2 + 1/4 + 1/7 + 1/8 + 1/9)

+ 0.3 (1/4 + 1/7 + 1/8 + 1/9)

+ 0.5 (1/7 + 1/8 + 1/9)

+ 0.9 (1/8 + 1/9)

+ 1/9

Con gli insiemi livello dati da:

A

A

A

A

A = 9

In molti casi gli insiemi livello fuzzy possono sostituire la classica funzione di appartenenza. Per esempio sia A un fuzzy set su X e A_a il suo insieme livello, A_a può essere scritto (m_A a,1]), cioè l'immagine inversa dell'intervallo [a,1] nell'insieme [0,1]:

m_Aa(x) = m _a m_A(x)) " x X.

10. ALTRE OPERAZIONI

Se A ,...,A_k sono sottoinsiemi fuzzy di X, e w ,...,w_k sono pesi non negativi che si sommano all'unità, allora una combinazione convessa di A ,...,A_k è un fuzzy set la cui funzione di appartenenza è espressa da:

m_A= w m_A + w_k m_Ak

dove in questo caso il simbolo + indica la somma aritmetica. Il concetto di una combinazione convessa è utile nella rappresentazione dei modificatori linguistici come "essenzialmente" e "tipicamente" modificano i pesi associati alle componenti di un fuzzy set.

Se A ,...,A_k sono sottoinsiemi fuzzy di X ,...,X_k rispettivamente, il prodotto cartesiano di A ,...,A_k è denotato con A x A x .... x A_k ed è definito come un sottoinsieme fuzzy di X x X x .... x X_k la cui funzione di appartenenza è espressa da:

m_{A x A x .... x Ak} (x ,...,x_k m_A (x m_Ak(x_k

Equivalentemente:

A x A x .... x A_k

_{X x...xXk} m_A (x m_Ak(x_k) / (x ,...,x_k

Esempio 10.1

Sia X=

e A = 0.8 / 3 + 1 / 5 + 0.6 / 6, B + 0.7 / 3 + 1 / 4 + 0.5 / 6

Allora A B = 0.8 / 3 + 1 / 4 + 1 / 5 + 0.6 / 6

A B = 0.7 / 3 + 0.5 / 6

A' = 1 / 1 + 1 / 2 + 0.2 / 3 + 1 / 4 + 0.4 / 6 + 1 / 7

AB = 0.56 / 3 + 0.3 / 6

A² = 0.64 / 3 + 1 / 5 + 0.36 / 6

0.5A = 0.4 / 3 + 0.5 / 5 + 0.3 / 6

CON(B) = 0.49 / 3 + 1 / 4 + 0.25 / 6

DIL(B) = 0.84 / 3 + 1 / 4 + 0.7 / 6

A B = 1 / 3 + 1 / 4 + 1 / 5 + 1 / 6

A B = 0.1 / 3 + 1 / 5 + 0.1 / 6

²A = 0.8 / 9 + 1 / 25 + 0.6 / 36

³A = 0.8 / 27 + 1 / 125 + 0.6 / 216

Esempio 10.2

Sia X = X = e siano

A A₂ = 1 / 2 + 0.6 / 4

allora A x A

11. CARDINALITA' DI UN FUZZY SET.

Nel caso di un sottoinsieme crispy, (non fuzzy), A, di un universo U, la proposizione "u è un elemento di A" è o vera o falsa, e da ciò segue che c'è soltanto un modo in cui la cardinalità di A, cioè il numero di elementi di A, può essere definita. Nel caso di un sottoinsieme fuzzy, F, di U, la proposizione "u è un elemento di F" è generalmente vera, basandoci sul significato del concetto di cardinalità.

Fra le differenti definizioni di cardinalità, alcuni associano ad un fuzzy set, F un numero reale, nel qual caso la cardinalità di un fuzzy set è non fuzzy. Altri associano ad F un numero fuzzy, poichè può essere dimostrato che la cardinalità di un fuzzy set dovrebbe essere un numero fuzzy.

Per completezza illustriamo ora un approccio alternativo al concetto di cardinalità.

Cardinalità scalare.

Quando X è un insieme finito, la cardinalità |A| di un fuzzy set A su X è definita come:

|A| = S_{x X} m_A(x)

|A| è detta anche potenza di A.

Cardinalità relativa:

||A|| = |A| / |X|

Interpretazione: proporzione di elementi di X che sono in A.

Quando X è non finito, |A| non sempre esiste

Se A ha supporto finito

|A| = S_{x suppA} m_A(x)

Altrimenti se X è un insieme numerabile e P è una misura su X

_x dP(x) = 1)

||A|| può essere la somma pesata

∫_x m_A(x) dP(x)

L'introduzione della funzione peso P assomiglia ad una "fuzzificazione" dell'universo X.

Questo può essere fatto in maniera più diretta scegliendo un fuzzy set Z su X costituito dalle parti più significative dell'universo X. Z è assunto avere un supporto finito o potenza finita. La cardinalità relativa di A sarà allora ||A Z||.

Cardinalità fuzzy di un fuzzy set.

Strettamente parlando la cardinalità di un fuzzy set sarebbe un "fuzzy numero".

Quando A ha un supporto finito, la sua cardinalità fuzzy è

|A|_f =S a /|A_a

dove A_a è l'insieme livello di A. [Zadeh 1977].

12. INCLUSIONE ED UGUAGLIANZE DI FUZZY SETS.

Le definizioni di inclusione e di uguaglianza di Zadeh possono apparire molto strette, specialmente perchè i valori di appartenenza precisi sono essenzialmente fuori portata.

a) Inclusione nel senso di Zadeh

A incluso in B sse

"x X m_A(x) ≤ m_B(x)

L'inclusione è una relazione di ordine su P(X).

Confronto di operatori:

" A,B P(X)  A.B incluso in A B

A B incluso in A + B

b) Inclusione ed uguaglianza debole.

Un modo per indebolire l'inclusione dei fuzzy sets è dato dalle seguenti definizioni:

x " a-appartiene" ad A sse x A_a

A è "debolmente incluso" in B,(denotato con A _a B) quando tutti gli elementi di X " a-appartengono" ad A o a B,

matematicamente

"x X max(1- m_A(x) , m_B(x) ) ≥ a

Praticamente, A _a B non è vero quando

esiste un x di X tale che m_A(x) >1 - a e m_B(x)<a

Quindi _a è transitiva solo per a >1/2.

La transitività per a= 1/2 può essere trovata modificando un poco la condizione precedente e stabilendo:

A _a/2 B sse per ogni x di X m_A(x) ≤ 1/2 o m_B(x) > 1/2

Possiamo voler imporre la condizione che l'inclusione di Zadeh sia un caso particolare di _a per esempio se

A incluso in B allora A _aa B

Questo vale solo per a ≤ 1/2. Quindi il solo transitivo _a consistente con tale inclusione è

Se a > 1/2 l'inclusione di Zadeh non implica _a poichè gli elementi x di X tali che

a < ( m_A(x) ≤ m_B(x) ) < a

non appartengono mai a (A' B)_a

L'uguaglianza di insiemi associata con è definita come

A uguale B sse A B e B A

A uguale B sse per ogni x di X

min[max(1- m_A(x) ,m_B(x)), max( m_A(x), 1- m_B(x) ] ≥ 1/2

che è equivalente a

max[min(m_A(x) ,m_B(x)), min(1- m_A(x), 1- m_B(x)) ] ≥ 1/2

L'uguaglianza debole ha la seguente interpretazione: Entrambi i valori di appartenenza m_A(x) e m_B(x) sono o maggiori o uguali ad 1/2 ed entrambi minori o uguali a 1/2.

Questa uguaglianza debole non è transitiva.

13. FUZZY SETS STRUTTURATI.

I fuzzy sets possono essere forniti di strutture algebriche. Sia * una legge di composizione su X.

Un fuzzy set A è chiuso rispetto a * se e solo se

"x X, "x X

m_A(x *x ) ≥ min( m_A(x m_A(x

Se (X,*) è un gruppo, un sottogruppo fuzzy A di X soddisfa la disuguaglianza precedente e l'uguaglianza:

m_A(x^-1) = m_A(x) dove x^-1x = e (e identità)

14. L-FUZZY SETS.

Sia L un insieme

Un L-fuzzy set A è associato ad una funzione m_A dall'universo X ad L. Se L ha una data struttura, come di reticolo o di gruppo, P_L(X), insieme degli L-fuzzy sets su X, avrà anchesso questa struttura.

Esempio 14.1

L reticolo.

L'intersezione e l'unione di L-fuzzy sets possono essere indotte attraverso le formule:

m_C(x) = inf ( m_A(x) , m_B(x) ) per ogni x X

m_D(x) = sup ( m_A(x) , m_B(x) ) per ogni x X

dove inf e sup denotano rispettivamente il più piccolo limite superiore ed il più grande limite inferiore.

Notiamo che i valori di appartenenza degli L-fuzzy sets non possono essere sempre confrontati a meno che L sia linearmente ordinato.

Inoltre, distributività e complementazione richiedono che sia definita una struttura più ricca.

Possono occorrere alcune situazioni per cui sono utili da considerare insiemi di valutazione diversi da [0,1].

Per esempio, se m ordinari fuzzy set A_i (i=1,...,m) in X corrispondono ad m proprietà, è possibile associare ad ogni x di X il vettore dei valori di appartenenza [m_Ai (x) ] che rappresenta il grado con cui x soddisfa le proprietà. Può essere costruita una funzione da X all'insieme L=[0,1]^m e L è un reticolo completo che non è un ordinamento lineare.

Ora assumiamo che ogni elemento x di X è descritto tramite una sola proprietà tra A ,...,A_m, supponendo quella più significativa per x. La proprietà che meglio descrive un elemento x'≠x può essere differente da quella che descrive x. Otteniamo in questo modo una partizione di X in m classi. Ovviamente, ciò è insignificante per confrontare valori di appartenenza di elementi di classi diverse. Così, l'insieme di valutazioni è qui una collezione di m ordinamenti lineari disgiunti.

Si può ovviamente estendere il concetto di fuzzy set in una gerarchia di k tipi di fuzzy sets in modo ricorsivo:

un fuzzy set di tipo 1 è un ordinario fuzzy set in X,

un fuzzy set di tipo k (k>1) in X è un L-fuzzy set i cui valori di appartenenza sono fuzzy sets di tipo k-1 su [0,1].

15. FUZZY SETS DI TIPO m.

Fino ora abbiamo considerato fuzzy set con funzioni di appartenenza che si definiscono crispy o gradi di appartenenza. Zadeh [1973a,p.52] perciò suggerì la nozione di fuzzy set la cui funzione di appartenenza è essa stessa un fuzzy set. Se noi chiamiamo fuzzy set, come li abbiamo considerati fino ad ora, come fuzzy set di tipo 1 allora fuzzy set di tipo 2 possono essere definiti come segue.

Definizione 16.1

Un fuzzy set di tipo 2 è un fuzzy set i cui valori di appartenenza sono fuzzy set di tipo 1 su [0,1].

Le operazioni di intersezione,unione e complemento definite fino ad ora non sono più adeguate per fuzzy set di tipo 2. Comunque, posteciperemo le discussioni sugli operatori adeguati fino a quando non avremo presentato il principio di estensione. Una naturale estensione di questi fuzzy set di tipo 2 è perciò la definizione di fuzzy set di tipo m.

Definizione 16.2

Un fuzzy set di tipo m è un fuzzy set in X i cui valori di appartenenza sono fuzzy set di tipo m-1, m>1 su [0,1].

I fuzzy sets di tipo m sono definiti anche ricorsivamente come segue:

i. un fuzzy set di tipo 1 è un fuzzy set ordinario su X.

ii. un fuzzy set di tipo m (m>1) è un insieme fuzzy la cui funzione di appartenenza è un insieme fuzzy di tipo m-1 su [0,1].

In questo contesto l'unione, l'intersezione ed il complemento di un fuzzy set di tipo m possono essere definite ricorsivamente per induzione dalla struttura dell'insieme di valutazione.

Denotate queste operazioni come _{m m}, '^m abbiamo per esempio

m_{A mB}(x)= m_A(x) _m-1 m_B(x)

m>1

I fuzzy sets di tipo 2 sono per noi i più interessanti.

I fuzzy sets di tipo 2 sono i fuzzy sets i cui gradi di appartenenza sono anch'essi insiemi fuzzy. Essi sono intuitivamente quegli insiemi fuzzy in cui gli elementi non hanno un grado di appartenenza preciso.

Più precisamente un fuzzy set di tipo 2, A è caratterizzato da una funzione fuzzy di appartenenza m_A come:

m_A : X ---> [0,1]^[0,1]

dove il valore m_A(x), è il "grado fuzzy" ed è un fuzzy set nell'intervallo unità [0,1] rappresentato da:

m_A (x) f(u)/u u

dove f è una funzione di appartenenza per il grado fuzzy m_A(x) ed è definita come:

f: [0,1] ---> [0,1]

Notiamo che la funzione di appartenenza di un insieme classico di tipo 2 è una corrispondenza da X all'insieme P() di sottoinsiemi classici di ,

P() = , , }

Una possibile interpretazione dei quattro valori di appartenenza è:

m_A(x) = ĝ   x A (come x A) è indefinito ed assurdo

m_A(x) = x A

m_A(x) = x A

m_A (x) = non sappiamo se x A o se x A.

Esempio 16.1

Consideriamo un fuzzy set di secondo tipo

A = valore delle monete

potrebbe essere formalizzato come:

A=medio/100L.=medio/200L.+basso/50L.+alto/500L.+basso/10L.

dove con le label medio, basso, alto indichiamo altri fuzzy sets che possiamo definire come

basso = 1/0.1 + 0.8/0.2 + 0.6/0.3 + 0.3/0.4

medio= 0.5/0.3 + 0.7/0.4 + 1/0.5 + 0.6/0.6 +0.4/0.7

alto = 0.5/0.7 + 0.7/0.8 + 0.8/0.9 + 1/1

16. MISURE FUZZY E MISURE DI FUZZINES.

Misure fuzzy

Per prevenire confusioni in merito alle misure fuzzy e alle misure di fuzziness, per prima cosa descriveremo brevemente il significato e le caratteristiche delle misure fuzzy. Nel lontano 1970, Sugeno definì una misura fuzzy come segue:

Definizione 1

Dato un campo di Borel ß su di un universo arbitrario X. Una funzione di insieme g definita su ß che ha le seguenti proprietà è chiamata una misura fuzzy:

1) g(Ĝ)=0, g(X)=1.

2) Se A, B ß e B A, allora g(A) ≤ g(B).

3) Se A_n ß, A_n A_n-1 ........ allora

lim _n-->oo g(A_n ) = g(lim_n-->oo A_n

La misura di Sugeno differisce dalla misura classica essenzialmente per la proprietà additiva [Murofushi e Sugeno 1989,p.201]. Un approccio differente è quello utilizzato da Klement e Schwyhla [1982].

Banon [1981] mostra che molte misure con universo finito del tipo di misura probabilità, funzioni di credibilità, misure di plausibilità, ed altre, sono misure fuzzy secondo la definizione di Sugeno. In questo contesto, una misura, quella di possibilità, è di particolare interesse [Dubois e Prade 1988a,p.7].

Nella teoria della struttura dei fuzzy sets Zadeh introdusse la nozione di distribuzione di probabilità e il concetto di misura di possibilità che rappresenta uno speciale tipo di misura fuzzy proposta da Sugeno. Una misura di possibilità è definita come segue [Zadeh 1978, Higashi e Klir 1982]

Definizione 2

Sia P(X) l'insieme potenza di un insieme X. Una misura di possibilità è una funzione

: P(x) --> [0,1]

con le eguenti proprietà:

1) π(Ĝ)=0, π(X)=1.

2) A incluso in B => π(A)≤π(B).

3) π( U_{i I} A_i )= sup_{i I} π(A_i ) con I insieme di indici.

Essa può essere univocamente determinata mediante una funzione di distribuzione di possibilità:

f: X-->[0,1] con π(A)= sup_{x A} f(x), X A.

Segue direttamente che f è definita da:

f(x)= π() per ogni x X [Klir e Floger 1988,p.122].

Una possibilità non è sempre una misura fuzzy [Puri e Ralescu 1982]. Ad ogni modo, questa rappresenta una misura fuzzy se X è finito e se la distribuzione di possibilità è normale cioè se ha valori compresi nell' intervallo [0,1].

Esempio 1

Sia X=, π="possibilità che x sia vicino a 8"

x   0 1 2 3 4 5 6 7 8 9 10

.0 .0 .0 .0 . 0 .1 .5 .8 1 .8 .5

π(A)= posssibilità che A contenga un intero vicino a 8

X A => π(A)=sup_{x A}

Per A= calcoliamo:

π(A)=sup_{x A} π()= sup,π,π}= sup =.8.

Misure di fuzziness

Le misure di fuzziness, in contrasto con le misure fuzzy, provano ad indicare il grado di fuzziness di fuzzy set.

Esistono vari tipi di approcci a questo scopo.

Alcuni autori, fortemente influenzati dall'entropia di Shannon come misura dell'informazione e seguendo de Luca e Termini [1972], considerano una misura di fuzziness come una applicazione d dall'insieme potenza P(X) a [0,+∞] soddisfacente determinate condizioni.

Altri [Kaufmann 1975] suggerirono un indice di fuzziness rappresentato da una distanza normalizzata, altri ancora [Yager 1979, Higashi e Klir 1982] considerano una misura di fuzzy come il grado di distinzione tra il fuzzy set ed i suoi complementi. Come esempio discuteremo di due di queste misure supponendo per entrambe i casi che il supporto di A sia finito.

La prima è:

Sia µ_A(x) la funzione di appartenenza del fuzzy set A per x X, con X finito.

Risulta plausibile che la misura di fuzziness d(A) dovrebbe avere le seguenti proprietà [de Luca e Termini 1972]:

1) d(A)=0 se A è un crispy set in X.

2) d(A) ha un unico valore massimo se µ_A(x)=1/2 x X

3) d(A) ≥ d(A') se A' è più crispy di A, per esempio se

µ_A'(x) ≤ µ_A(x)    per µ_A(x) ≤ 1/2   e

µ_A(x) ≥ µ_A'(x)    per µ_A(x)≥ 1/2.

4) d(A') = d(A) dove A' indica il complemento di A .

De Luca e Termini suggerirono, come misura di fuzziness, l' "entopia" di un fuzzy set [de Luca Termini 1972,p.305] che essi definirono come segue:

Esempio 1

Sia A="interi vicini a 10"

A=

Sia K=1, così:

d(A)=.325+.693+.506+0+.506+.693+.325=3.038

Sia inoltre B="interi strettamente vicini a 10"

B=

d(B)=.325+.611+.673+.611+0+.501+.693+.611+.325=4.35

La seconda è:

Knopfmacher [1975], Loo [1977], Gottwald [1979b], ed altri si basarono, per i loro contributi, sui suggerimenti di de Luca e Termini.

Se A è un fuzzy set in X e A' è il suo complemento, allora, contrariamente a quanto avviene per gli insiemi crispy, non è necessariamente vero che :

A A' = X

A A' = Ĝ

Il fatto che i fuzzy sets non sempre soddisfano la legge del "mezzo escluso" è una delle maggiori distinzioni tra i fuzzy sets e i tradizionali insiemi crispy.

Alcuni autori [Yager 1979, Higashi e Klir 1982] considerano le relazioni tra A e A' l'essenza di fuzziness. Yager [1979] nota che la distinzione tra A ed il suo complemento A' non è soddisfatta dai fuzzy sets. Egli, quindi, suggerisce che una misura di fuzziness sarebbe una misura della mancanza di differenza tra A e A' o tra µ_A(x) e µ_A'(x).

E' interessante anche determinare indici scalari per misurare il grado di fuzzines di un fuzzy set.

Il grado di fuzzines si assume per esprimere su un livello globale la difficoltà di decidere quali elementi appartengono e quali non appartengono ad un dato fuzzy set.

Matematicamente una misura di fuzzines è una corrispondenza d da P(X) a [0,+∞) che soddisfa le condizioni:

1)d(A)=0 sse A è un sottoinsieme ordinario di X

2)d(A) è massimo sse m_A(x)=1/2 "x X

3)d(A*)≤d(A) dove A* è una versione affinata di A cioè

m_A*(x)≤ m_A(x) se m_A(x) ≤1/2 e

m_A*(x)≥ m_A(x) se m_A(x)≥1/2

4)d(A) = d(A') (A' è un fuzzy set come A).

Quando X è finito, Loo ha proposto una forma generale matematica per d

d(A) = F [S_i=1,...,|X| c_i f_i( m_A(x_i))]

dove c_i R⁺ "i;

f_i è una funzione a valori reali tale che f_i(0)=f_i(1)=0;

f_i(u)=f_i(1-u) "u e f_i è strettamente crescente su [0,1/2].

F è una funzione crescente, positiva che soddisfa le 1),...4) ma non è a priori la forma più generale.

Quando F è lineare, vale la proprietà

d(A) + d(B) = d(A B)+ d(A B)

Forme particolari di d sono:

Indice di fuzzines: F è l'identità ...

Entropia: F(u) = ku k>0, e per ogni i c_i =1

f_i(u) = -u log (u) - (1-u) log(1-u) (funzione di Shannon)

Le misure di fuzziness valutano A e A' al tempo stesso.

. FUZZY SET CONVESSO

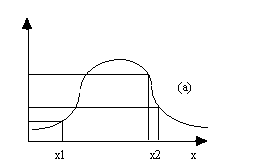
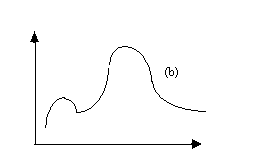
La nozione di convessità può essere generalizzata a fuzzy sets di un universo X, che assumeremo essere uno spazio euclideo n-dimensionale.

Un fuzzy set A è convesso se e solo se i suoi insiemi livello sono convessi.

Un'equivalente definizione di convessità è:

A è convesso se e solo se

"x ,x X, "p

m_A(px +(1-p)x ) ≥ min [ m_A(x m_A(x

nota: questo non implica la convessità della funzione m_A(x).

Diamo di seguito un esempio grafico di fuzzy set convesso (a) e di fuzzy set non convesso (b).

18. NUMERO FUZZY

Un numero fuzzy è un insieme fuzzy il cui universo coincide con l'insieme dei numeri reali X=R. (E' un fuzzy set normalizzato A della retta reale R).

La sua funzione di appartenenza sarà quindi:

m_A: x X=R ----> m_A(x)

Un fuzzy set A definito sui reali ed a valori in [0,1] è un numero fuzzy se e solo se

- A è convesso

- esiste un solo punto x_o R tale che m_A(x_o)=1

(x_o è detto valor medio)

m_A è continua a tratti.

L'importanza dei numeri fuzzy è quella di potersi ricollegare alla teoria classica della matematica dei numeri, attraverso il principio di estensione introdotto da Zadeh.

Analizzando la definizione della funzione di appartenenza di un numero fuzzy ci accorgiamo di essere di fronte alla definizione di una funzione di reali sull'intervallo [0,1].

Abbiamo visto che un numero fuzzy è un insieme fuzzy A con funzione di appartenenza:

m_A :R --> [0,1]

tale che, indicato con U l'universo del discorso si ha:

1)il supporto [A]_h= è un intervallo chiuso;

x U m_A(x)=1

m_A l x l)x )≥ min( m_A(x m_A(x )) con lÎ[0,1].

Quello che cerchiamo ora è una rappresentazione dei numery fuzzy.

La classe dei numeri fuzzy presa da noi in considerazione è quella dei "Flat fuzzy number ", dal momento che essa presenta tutti gli aspetti, convenienti e positivi, tipici delle funzioni lineari, proponendo dei meccanismi di sviluppo di operazioni non riscontrabili in altre classi.

Un Flat Number è un numero fuzzy M tale che:

(m,n) R con m≤n e m_M(x)=1 "x [m,n].

Ogni numero appartenente a questa classe è di tipo L-R ed è caratterizzato da una funzione di appartenenza definita come segue:

m_M(x) = L[(x-m)/(m-1)] se x [1,m]

1 se x [m,n]

R[(x-n)/(n-u)] se x [n,u]

0 altrimenti

con L(a) e R(b) funzioni crescenti e decrescenti nei relativi intervalli, m ed n valori modali e 1 ed u intersezioni di L(a) e R(b) con l'asse delle x.

Una rappresentazione simbolica di tali numeri è fornita dalla quadrupla [1,m,n,u] che offre tutte le caratteristiche di una facile gestione.

Per i nostri scopi consideriamo una sottoclasse dei Flat Number indicata come gli L-L Number Fuzzy, con L(a) funzione lineare con le caratteristiche citate.

Le scelte fatte e le proprietà della funzione di appartenenza ci permettono di manipolare numeri fuzzy di tipo trapezoidale. Tale classe comprende, chiaramente, sia numeri triangolari che numeri rettangolari fuzzy, dipendentemente dai parametri 1,m,n,u.

I vantaggi offerti dai numeri trapezoidali si evidenziano sia nella fase implementativa che in quella operazionale.

Gli svantaggi nascono dalle restrizioni imposte dalla linearità delle parti crescenti e decrescenti.

Il numero fuzzy risulta il punto di incontro tra la potenza concettuale fuzzy, e la grossa teoria dei numeri trattata dall'analisi matematica.

Con il principio di estensione introdotto da Zadeh è possibile estendere concetti matematici non fuzzy per poterli utilizzare su elementi fuzzy.

19. PRINCIPIO DI ESTENSIONE

Il principio di estensione è uno dei principali concetti della teoria dei fuzzy sets ed è uno strumento utilissimo per generalizzare i concetti matematici crispy ai fuzzy sets.

Nella sua forma elementare fu già utilizzato da Zadeh [1965], nel suo primo contributo. Allo stesso tempo furono suggerite delle modifiche [Zadeh 1973a, Zadeh 1975, Jain 1976].

Esempio 1

Sia A=

f(x)= x²

Allora applicando il principio di estensione otteniamo

B=f(A)== (Figura 1)

Il principio di estensione può essere modificato utilizzando la somma algebrica piuttosto che sup ed il prodotto algebrico piuttosto che min [Dubois e Prade 1980a]. In generale, comunque, il principio di estensione è usato così come è stato definito e noi limiteremo le nostre considerazioni a questa classica versione.

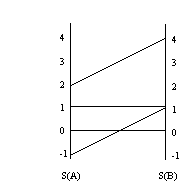
FIGURA .1

Equivalentemente possiamo dire che: supponendo che f sia una applicazione da X ad Y ed A un sottoinsieme fuzzy di X espresso come:

A = m /x m_n/x_n

Allora il principio di estensione asserisce che

f(A) = f(m /x m_n/x_n m /f(x m_n/f(x_n

Così l'immagine di A tramite f può essere dedotta dalla conoscenza dell'immagine di x₁,...x_n tramite f.

Sia X un prodotto cartesiano di universi

X = X x x X_r e siano

A ,...,A_r r fuzzy sets definiti su

X ....,X_r rispettivamente, con le relative funzioni di appartenenza.

Si abbia poi una funzione n-aria f, la quale è un'applicazione del prodotto cartesiano X ad un universo Y tale che y=f(x ,...x_n

Il prodotto cartesiano di A ,...,A_r è definito come:

A x xA_r

= _{X x...xXr} min( m_A (x m_Ar(x_r))/(x ...x_r

Il principio di estensione di Zadeh ci permette di indurre dagli r fuzzy sets A_i, un fuzzy set F su Y attraverso f così che

m_F(y)=supy = f( x ...,x_r) min[ m_A (x m_Ar(x_r

m_F(y)=0 se f^-1(y)=ĝ

dove f^-1(y) è l'immmagine inversa di y.

Definito questo principio, lo si può utilizzare per rendere fuzzy qualsiasi dominio della teoria matematica basato sugli insiemi.

Ci piace qui ricordare a tale proposito una frase di Gaines [1975]:

".... il fondamentale cambiamento è quello di sostituire il concetto che una variabile ha un valore con il concetto fuzzy che una variabile ha un grado di appartenenza ad ogni possibile valore."

Esempio 2

Dato X=1+2+...+7 e sia "grande" un sottoinsieme fuzzy su X definito da "grande" = 1/1 + 1/2 + 0.8/3 + 0.5/4. Se prendiamo f come l'operazione di elevamento al quadrato, allora:

f(grande) = ²grande = (grande²) = 1/1 + 1/4 + 0.8/9 + 0.5/16.

Chiaramente, con il principio di estensione, possiamo rendere fuzzy ogni dominio di argomentazione matematica usando la teoria degli insiemi. Dovrebbe essere chiaro, comunque, che un altro modo di rendere fuzzy una struttura è appunto sostituire insiemi non fuzzy tramite insiemi fuzzy o tramite la famiglia dei loro insiemi livello nella intelaiatura della struttura.

20.OPERAZIONI PER I FUZZY SETS DI TIPO 2

Intersezione, unione e complemento

Il principio di estensione può essere utilizzato per definire un insieme di operazioni teoriche per i fuzzy sets di tipo 2. Considereremo solo fuzzy sets di tipo 2 con dominio discreto.

Siano:

A(x)= e B= due fuzzy sets di tipo 2

dove:

_A(x)=

_B(x)=

Gli u_i ,v_j rappresentano il grado di appartenenza del fuzzy set di tipo 1 e i µ_ui, µ_vj, rispettivamente, le loro funzioni di appartenenza. Usando il principio di estensione, l'insieme di operazioni teoriche sopra mensionato può essere definito come segue [Mizumoto e Tanaka 1976]:

Consideriamo i due fuzzy sets sopra definiti. La funzione di appartenenza della loro unione è allora definita da:

_{A B}(x)= µ_A(x) U µ_B(x)=

= , u_i ,v_j

Dove:

_{A B}(w)= sup _w=max min.

La loro intersezione è definita da:

_{A B}(x)=µ_A(x) _B(x)=

, u_i ,v_j

Dove:

_{A B}(w)= sup_w=min min

ed il complemento è definito da:

_A'(x)= .

Esempio 1

Sia X=1,2,...,10

A = "interi piccoli", B = "interi vicini a 4"

definiti da:

A=, B=

dove per x=3

_A

_B

computiamo

u _i v _j w=min µ_ui (3) µ_vj (3) min

1 .8 1 1 1

.8 .8 1 .5 .5

.7 .7 1 .3 .3

1 .7 .5 1 .5

.8 .7 .5 .5 .5

1 .6 .4 1 .4

.6 .8 .6 .4 .5 .4

.6 .7 .6 .4 .3 .3

Poi abbiamo da computare l' estremo superiore del grado di appartenenza di tutte le coppie (u_i ,v_j) che producono w come minimo:

sup _=min =1

sup _=min =.5

sup _=min =.4

Così otteniamo la funzione di appartenenza di x=3 come il fuzzy set µ_{A B}

Mizumoto e Tanaka [1976,p.318] mostrano che i fuzzy set di tipo 2 sono: idempotenti, commutativi, associativi e soddisfano alle leggi di De Morgan. Del resto essi non sono distributivi, non soddisfano alle leggi di assorbimento, identità e del complemento. Il precedente esempio è un buon esempio della facilità di computazione richiesta dalle operazioni con i fuzzy sets di tipo 2. Il lettore può rendersi conto che il grado di appartenenza di uno solo degli elementi del fuzzy set di tipo 2 è noto a priori. Per tutti gli altri c' è bisogno del relativo calcolo.

21 Operazioni algebriche con i numeri fuzzy

Un numero fuzzy M è un fuzzy set convesso normalizzato del campo reale R come questi:

1) Esiste esattamente un x_o di R con µ_M (x_o)=1 (x_o è chiamato valor medio di M)

2) µ_M(x) è l' ampiezza continua del pezzo.

Attualmente la definizione data è molto spesso modificata. Per amore della efficienza computazionale e per la comodità della acquisizione dei dati, spesso, sono state usate funzioni di appartenenza trapezzoidali. La figura mostra un fuzzy set, che potrebbe essere chiamato "approssimativamente 5" e che normalmente è definito dalla quadrupla . Per esattezza questo non rappresenta un intervallo fuzzy.

Un numero fuzzy triangolare è naturalmente un caso speciale di questo appena trattato.

Un numero fuzzy M è detto positivo (negativo) se la sua funzione di appartenenza è tale che:

_M(x)=0, per ogni x<0 ( per ogni x>0).

Numero fuzzy trapezoidale.

Esempio 21.2

I seguenti fuzzy sets sono numeri fuzzy:

"approssimativamente 5" =

"approssimativamente 10" =

ma non è un numero fuzzy poichè µ(4) e µ(5) sono entrambe uguali a 1.

Abbiamo tutti familiarità con le operazioni algebriche con i numeri crispy. Se vogliamo utilizzare i fuzzy sets nelle applicazioni noi avremo a che fare con i numeri fuzzy ed il principio di estensione è una strada per estendere le operazioni dai numeri crispy ai numeri fuzzy.

Ci occorrono delle definizioni :

Siano F(R) l' insieme dei numeri fuzzy reali e X= X X

Possiamo definire le seguenti operazioni binarie:

Definizione 1

Un' operazione binaria * in R è chiamata crescente (decrescente) se :

per x > y e x > y

x * x > y * y (x * x < y * y )

Esempio 21.3

f(x,y) = x+y operazione crescente

f(x,y) = x*y operazione crescente in R

f(x,y) = -(x+y) operazione decrescente

21 Operazioni estese per la rappresentazione LR dei numeri fuzzy

L' efficienza computazionale è di particolare interesse quando si utilizza la teoria dei fuzzy sets per risolvere problemi reali. Quindi, nel seguito, considereremo in dettaglio la rappresentazione LR dei fuzzy sets, che aumenta l'efficienza computazionale senza diminuire, oltre limiti accettabili, la generalità. Dubois e Prade [1979] suggeriscono uno speciale tipo di rappresetazione per i numeri fuzzy. Essi definiscono, L (e R), che vanno da R⁺ a [0,1] e sono decrescenti, come funzioni shape se L(0)=1, L(x)<1 per ogni x>0;

L(x)>0 per ogni x<1; L(0)=1 oppure ( L(x)>0, per ogni x, e L(+∞)=0).

Definizione 21.2

Un numero fuzzy M è di tipo LR se esistono funzioni di riferimento L (per sinistra) R (per destra) e degli scalari a >0, b >0 con:

_M(x) = L( (m-x)/ a) ) per x ≤ m

R( (x-m) / b)) per x ≥ m

m, chiamato valor medio, di M, è un numero reale, a b sono rispettivamente chiamati distribuzione sinistra e destra.

Simbolicamente M è denotato con (m, a b _LR (vedi figura).

LR-rappresentazione di numeri fuzzy

Per L(z) possono essere scelte differenti funzioni. Dubois e Prade [1988a, p.50], propongono come esempio:

L(x)=max(0, 1-x)^p ; L(x)=max(0, 1-x^p ); con p>0;

L(x)= e^-x o L(x)= e^-x2 .

Questi esempi danno gia un'impressione sulla vasta portata di L(z). Il problema è quello di trovare la funzione appropriata allo specifico contesto.