|
|
| |
ESPERIENZA N° 4: MISURA DI CORRENTI E DIFFERENZE DI POTENZIALE CON MULTIMETRO ANALOGICO E DIGITALE. DETERMINAZIONE CURVA CARATTERISTICA V-I DI UN CONDUTTORE E MISURA DI RESISTENZA CON METODO VOLTAMPEROMETRICO.
OBIETTIVO:
Studio dell'andamento della relazione corrente - differenza di potenziale applicata a due resistenze di diverso valore nominale, per una lampadina e per un led.
STRUMENTI :
N° 1 Basetta;
N° 1 Saldatore;
N° 1 Generatore di forza elettromotrice e continua;
N° 1 Multimetro digitale;
N° 1 Multimetro analogico;
N° 1 Resistenza di valore nominale di 120 W con tolleranza del 5%;
N° 1 Resistenza di valore nominale di 2.7 MW con tolleranza del 10%;
N° 1 Lampadina a filamento metallico con resistenza interna dell'ordine di 1 kW e 3 W di potenza;
N° 1 Led con resistenza interna dell'ordine di 1.2 kW
INTRODUZIONE TEORICA :
Gli elettroni liberi di un conduttore metallico isolato si muovono di moto casuale come le molecole di un gas racchiuso in un contenitore e la loro agitazione termica non dà luogo ad alcun moto direzionale netto. Se ai capi del conduttore in questione viene applicata una differenza di potenziale V allora nel conduttore stesso si stabilisce un campo elettrico che agisce sugli elettroni imprimendo loro un moto netto opposto ad E. E' possibile dare quindi la definizione di corrente se si immagina una sezione del conduttore e le cariche dq che attraversano la sezione nell'unità di tempo dt, allora i = dq / dt.
Se applichiamo una identica differenza di potenziale a conduttori geometricamente simili ma costituiti da diversi materiali, ne risultano correnti diverse, la caratteristica che entra in gioco è la resistenza elettrica. La resistenza di un conduttore tra due punti si determina applicando una differenza di potenziale V e misurando la corrente i che ne risulta. La resistenza R è data da:
![]()
Proviamo ad applicare ad un corpo una differenza di potenziale e misuriamo la corrente risultante. Ripetendo la misura per diversi valori della differenza di potenziale possiamo determinare la relazione che lega quest'ultima entità all'intensità di corrente. Nel caso in cui, per un determinato oggetto, la relazione che lega differenza di potenziale e corrente sia lineare diremo che l'oggetto è ohmico. Nei circuiti elettronici però esistono dispositivi che non obbediscono alla legge di Ohm e sono chiamati non ohmici, ad esempio avremo a che fare nell'esperienza con un dispositivo (il led) non ohmico e la relazione che lega la corrente i che attraversa il led alla differenza di potenziale ai capi del led stesso è non lineare e strutturata in un modo che esamineremo in seguito.
La raccolta dei dati per l'analisi della relazione tra V ed I è stata realizzata per mezzo del metodo voltamperometrico, che prevede la misura della differenza di potenziale e della corrente che attraversa un elemento al variare della forza elettromotrice che alimenta il circuito.
I circuiti che possono essere realizzati per uno studio della relazione V-I sono essenzialmente due sono schematizzati subito sotto e saranno indicati come circuito a e circuito b

![]()

![]()
Affermiamo subito che con entrambi i circuiti si commette un
errore sistematico nella determinazione della resistenza R, la differenza di
potenziale misurata dal voltmetro non è uguale al prodotto tra la resistenza
incognita e la corrente misurata dall'amperometro: in effetti vanno considerate
le resistenze interne degli strumenti che influenzano le grandezze coinvolte.
Nel primo circuito schematizzato non tutta la corrente misurata dall'amperometro attraversa la resistenza poiché una parte devia verso il voltmetro, allora possiamo scrivere considerando la corrente in gioco:
rielaborando otteniamo:
![]()
![]()
Nel caso in
cui sia RV>>RX, allora
![]()
E quindi
Nel secondo circuito schematizzato accade che la differenza di potenziale non è esattamente uguale alla caduta di tensione ai capi della resistenza incognita perché va considerata la resistenza interna dell'amperometro scriviamo allora considerando le differenze di potenziale:
![]()
![]()
Nel caso in
cui Ra<<Rx otteniamo:
Dalle relazioni appena indicate ci aspettiamo un andamento lineare tra differenza di potenziale e intensità di corrente.
Nella nostra esperienza considereremo anche un led, e analizzeremo la relazione che lega la corrente che lo attraversa con la differenza di potenziale ai suoi capi. Allo scopo consideriamo il circuito rappresentato di seguito:

Con lo scopo di non danneggiare il led è stata aggiunta una resistenza di protezione. Il led è un conduttore non ohmico: ha corrente che lo attraversa pari a zero per valori negativi di differenze di potenziale e corrente che cresce (sino a raggiungere un limite di saturazione) esponenzialmente per valori positivi di differenze di potenziale. Dovremo verificare questo particolare andamento.
Infine per lo studio della relazione tra corrente e differenza di potenziale nel caso della lampadina si è creato e studiato il circuito:

La lampadina è un oggetto la cui resistenza cambia al variare della intensità di corrente e quindi è un conduttore non ohmico.
PROCEDIMENTO :
Abbiamo effettuato una serie di misurazioni di corrente e differenze di potenziale sui circuiti descritti in precedenza ed alimentati da una forza elettromotrice continua e variabile tra +20 V e -20 V. Per le misure delle differenze di potenziale si è adoperato un voltmetro digitale che ha una precisione di 0.01 V quando il fondo scala è posto ad 20 V, mentre per le misure di corrente si è adoperato un amperometro analogico a bobina mobile con una precisione del 1% sul valore del fondo scala in uso.
Consideriamo trascurabile l'errore di lettura commesso nell'uso dell'amperometro analogico.
Si è fatta particolare attenzione a non danneggiare il led durante le misure e pertanto quando abbiamo lavorato con il circuito in sui era inserito il led abbiamo fatto variare la forza elettromotrice e tra -2.5 V e + 2.5 V.
Abbiamo raccolto nella Tabelle n° 1 e n° 2 i dati ricavati applicati ai primi due circuiti schematizzati applicando la resistenza nominale di 120 W. Nelle Tabelle n° 3 e n° 4 abbiamo espresso invece i dati raccolti con la resistenza nominale di 2.7 MW. Infine nelle Tabelle n° 5 e n° 6 abbiamo sistemato i dati relativi al circuito contenente il led ed il circuito contenente la lampadina.
ANALISI DEI DATI :
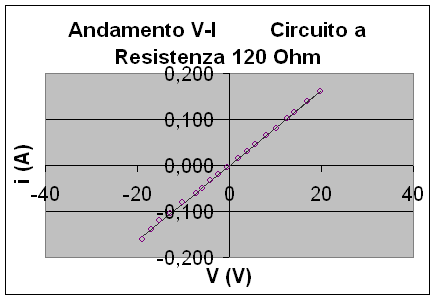
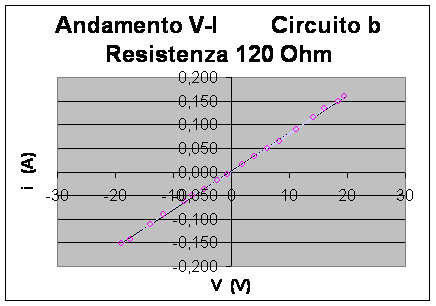
Diamo subito un'occhiata alle Tabelle n° 1 e n° 2 che riguardano le misure di corrente e differenza di potenziale misurate nei circuiti a e b prima schematizzati in corrispondenza di una resistenza del valore nominale di 120 W
Dalla base delle differenze di potenziale e dei valori di corrente rilevati abbiamo determinato la retta di regressione ed il coefficiente di correlazione lineare.
Il valore calcolato per il coefficiente di correlazione lineare nei due circuiti è pari a 0.9998 ed è quindi evidente che l'andamento tra V ed i è lineare visto che il coefficiente di correlazione lineare fornisce un giudizio su quanto le variabili V ed i siano in dipendenza lineare fra loro.
Dopo questo primo risultato possiamo vedere come sia possibile stimare il valore della resistenza inserita nel circuito. Possiamo assegnare tale valore adoperando due criteri distinti.
Un primo fissa come punto saldo la linearità tra V ed i e permette di valutare la resistenza come l'inverso della pendenza della retta andamento V-I, visto che V = i R. Un secondo metodo invece permette di calcolare il valore della resistenza andando a mediare su tutti i valori di resistenza ottenuti in corrispondenza delle singole rilevazioni.
Approfondiamo questi discorsi.
Il primo criterio quindi considera l'andamento V-I come rettilineo e permette di calcolare la resistenza come inverso della pendenza di tale retta. Noi però non conosciamo perfettamente tale retta e pertanto andremo a considerare una approssimazione di questa sulla base dei dati ottenuti sperimentalmente, questa approssimazione è la retta dei minimi quadrati.
![]()
Quindi
partendo dalla retta y = mx + q stimiamo R dalla relazione:
Banalmente possiamo anche determinare l'incertezza commessa nella valutazione di R con questo metodo, e dalla formula di propagazione degli errori otteniamo:
![]()
Dove sm è l'incertezza che abbiamo su m e deriva dall'utilizzo del metodo dei minimi quadrati.
Il secondo criterio per la stima di R considera invece la media pesata sui valori di resistenza Ri ottenuti nelle singole rilevazioni dell'esperienza ed gli errori commessi nelle singoli misurazioni ei. Quindi scriviamo:
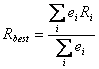
Dobbiamo ora valutare l'errore commesso sulla singola misura di Ri. Se consideriamo la definizione della resistenza:
![]()
dalla formula di propagazione degli errori otteniamo:
![]()
![]()
Allora risulta
che:
L'incertezza che si viene a creare su questa misura è:
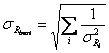
Il concetto di calcolare la media pesata sugli errori sta nel dare maggiore 'importanza' ai dati che sono meno affetti da errori per stimare il 'vero' valore di una grandezza.
Abbiamo applicato i due metodi appena descritti per stimare la resistenza R del valore nominale di 120 W, con una tolleranza del 5%, inserita nei circuiti a e b.
Abbiamo ottenuto per il primo circuito R = 122.2 W W ed Rbest = 123.8 W W mentre per il secondo circuito R = 123.9 W W ed Rbest = 124.06 W W; tutti questi valori sono in pieno accordo con il valore reale della resistenza che è compreso tra 114 W e 126 W. Però possiamo fare ulteriori considerazioni sui circuiti coinvolti nelle misure. Infatti una ipotesi fondamentale nella concezione del circuito b è:
![]()
e nel caso in cui RA<< RX otteniamo:
![]()
Ragioniamo quindi sui valori della resistenza dell'amperometro che variano a seconda del fondo scala adoperato in un determinato istante. Nella fattispecie abbiamo adoperato un fondo scala talvolta a 50 mA e talvolta a 500 mA che corrispondono ad una resistenza rispettivamente di 6.4 W e 0.64 W e questi valori non soddisfano pienamente la condizione RA<< RX, quindi possiamo pensare che per valori di resistenza da stimare più grandi il circuito b fornirà una stima più fedele.
Se invece consideriamo velocemente una ipotesi fondamentale su cui è basato il circuito a ed ovvero RV>>RX notiamo che questa condizione è pienamente verificata visto che nel voltmetro digitale in uso la resistenza interna è dell'ordine di 10 MW
Riassumendo possiamo affermare che entrambi i circuiti, come si è visto, forniranno una stima corretta, ma per grandi valori di resistenza da misurare il circuito b risulta essere più appropriato, mentre per piccoli valori di resistenza il circuito a è più adatto.
Questi discorsi hanno riscontro nel momento in cui siamo andati a stimare la resistenza del valore nominale di 2.7 MW, infatti abbiamo determinato per il primo circuito R = 2.3 MW W ed Rbest = 2.27 MW 0.021 MW mentre per il secondo circuito R = 2.9 MW 0.27 MW ed Rbest = 2.9 MW W. In questo caso abbiamo adoperato un fondo scala per l'amperometro analogico di 50 mA che corrisponde ad una resistenza interna di 2 kW, valore piccolissimo rispetto ai 2.7 MW
Per quanto riguarda il circuito in cui si è inserito il led abbiamo fatto una serie di misurazioni di corrente e differenze di potenziale ed abbiamo ottenuto i dati raccolti nella tabella n° 5 evidenziando nel grafico successivo l'andamento V-I che risulta essere in linea con quanto ci aspettavamo, ovvero per valori negativi di differenza di potenziale la corrente che attraversa l'elemento è nulla ed in seguito al crescere della differenza di potenziale applicata cresce esponenzialmente.
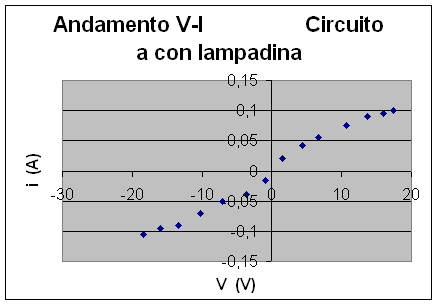
Ultimo caso di studio è invece il circuito in cui è inserita la lampadina che ha permesso di ottenere i dati espressi nella Tabella n° 6. Esprimendo questi dati in forma grafica si è evidenziato un comportamento per la resistenza R non costante, ma variabile a seconda della corrente e della differenza di potenziale applicate.
Tabella n° 1 : Misure corrente e d.d.p. con resistenza nominale di 120 W e circuito a
|
DV (V) |
Corrente I (A) |
Fondo Scala (A) |
Errore su I (A) |
Resistenza R (W |
Errore su R (W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = mx + q
m = 0.0082 q = -0.00039
sm sq
sy
r = 0.9998
R = 122.2 W sR W
Rbest = 123.8 W sRbest W
Tabella n° 2 : Misure corrente e d.d.p. con resistenza nominale di 120 W e circuito b
|
DV (V) |
Corrente I (A) |
Fondo Scala (A) |
Errore su I (A) |
Resistenza R (W |
Errore su R (W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = mx + q
m = 0.0081 q = -0.0011
sm sq
sy
r = 0.9998
R = 123.9 sR W
Rbest = 124.1 W sRbest W
|
DV (V) |
Corrente I (A) |
Fondo Scala (mA) |
Errore su I m(A) |
Resistenza R (MW |
Errore su R (W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = mx + q
m = 0.00044 q = -0.0000194
sm sq
sy
r = 0.9986
R = 2.3 MW sR W
Rbest = 2.27 MW sRbest W
|
DV (V) |
Corrente I (A) |
Fondo scala (mA) |
Errore su I (mA) |
Resistenza R (MW |
Errore su R (W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = mx + q
m = 0.00035 q = -0.00039
sm sq
sy
r = 0.99994
R = 2.9 MW sR 26.9 W
Rbest = 2.9 MW sRbest W
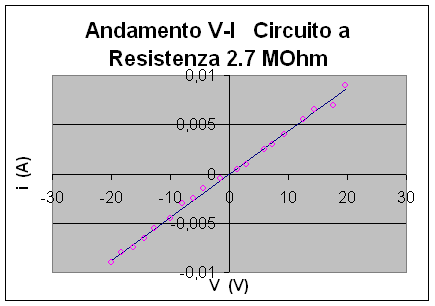
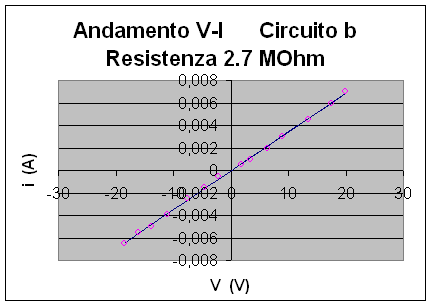
Tabella n° 5 : Misure corrente e d.d.p. con resistenza LED e circuito b
|
Ddp DV(V) |
Corrente I (A) |
Fondo Scala (A) |
Errore su I (A) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
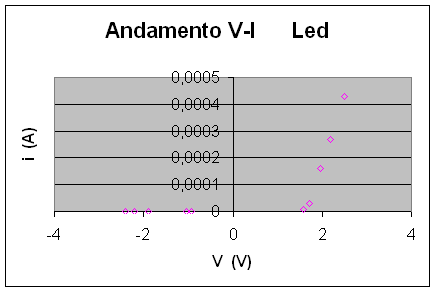
Tabella n° 6 : Misure corrente e d.d.p. con resistenza Lampadina e circuito b
|
Ddp DV(V) |
Corrente I (A) |
Errore su I (A) |
Resistenza R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026