RELAZIONE DI FISICA SUL MOTO DEL PENDOLO - ricercare la relazione tra il periodo e la lunghezza del pendolo

fisica

RELAZIONE DI FISICA SUL MOTO DEL PENDOLO

SCOPO: ricercare la relazione tra il periodo e la lunghezza del pendolo.

MATERIALE:

1. morsetto
2. peso
3. asta di sostegno
4. noce
5. astina
6. coccodrillo
7. spessore

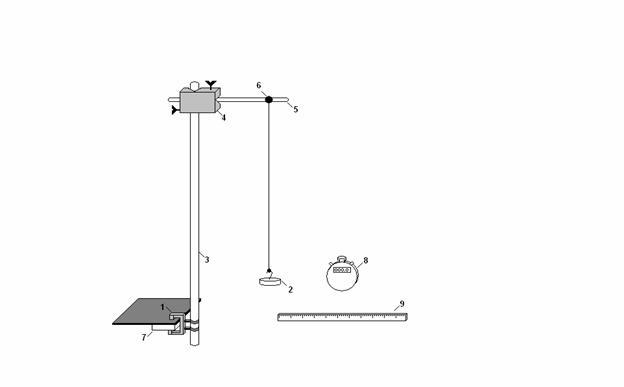
PROCEDIMENTO

Con un pendolo simile a quello riportato qua sopra, abbiamo svolto questo esperimento.

Per prima cosa abbiamo regolato la lunghezza del pendolo con il metro, successivamente abbiamo portato il pendolo ad un'inclinazione pari a 15° rispetto all'asse verticale di partenza; lo abbiamo fatto oscillare e abbiamo misurato il periodo che ci impiega per fare dieci oscillazioni. Poi abbiamo eseguito le precedenti operazioni cambiando progressivamente la lunghezza del pendolo da 0.2 a 1 metro.

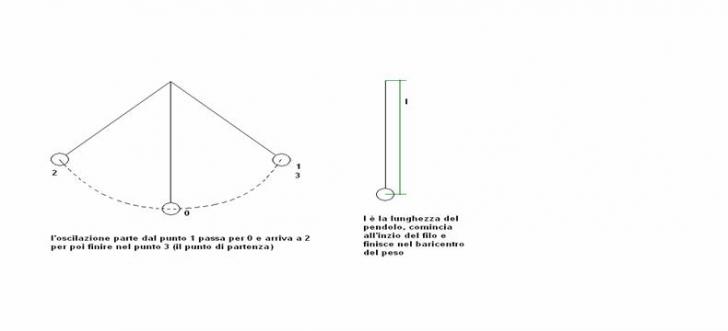
L = lunghezza del pendolo.

T= periodo di dieci oscillazioni.

T =  = periodo di un'oscillazione.

T = quadrato di T.

CALCOLI

1)    

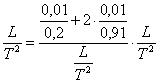
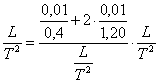
3)

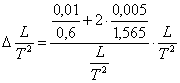
4)

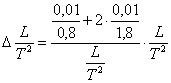
5)   

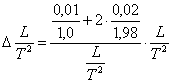
COSTRUZIONE GRAFICA

K =

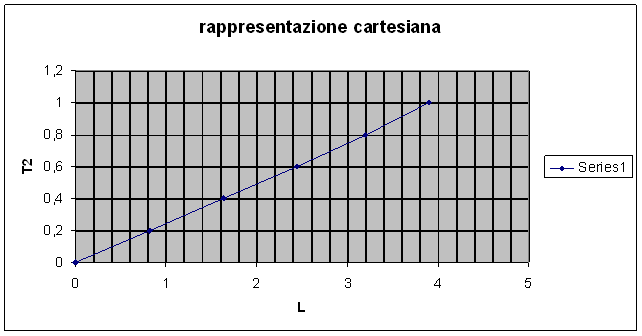
CONCLUSIONI

Dopo questo esperimento abbiamo visto che il tempo delle oscillazioni e la lunghezza del pendolo () sono direttamente proporzionali cioè il loro rapporto è sempre costante. Infatti, possiamo notare che con il pendolo a lunghezza 0,2 metri il tempo di un'oscillazione è di 0,91 secondi, mentre a lunghezza 1 metro il tempo è di 1,98 secondi .