|
|
| |
Onde elettromagnetiche
Le equazioni di Maxwell
A metà del diciannovesimo secolo si sapeva che campi magnetici variabili creavano campi elettrici, grazie alla legge di Faraday-Lenz. Però non era dimostrato che potesse avvenire il contrario, poiché l'interazione tra campi magnetici e correnti era allora data dalla legge di Ampere, che non metteva in relazione i due campi. L'opera di Maxwell fu quella di assumere come ipotesi che fosse possibile il contrario e da i suoi studi si ottenne la seconda grande sintesi della fisica, riassunta in quattro leggi fondamentali:
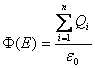 (Teorema di Gauss per il campo
elettrico)
(Teorema di Gauss per il campo
elettrico)Terza equazione di Maxwell
Possiamo facilmente ricavare la terza equazione partendo dalla legge di
Faraday-Lenz: ![]()
![]()
![]()
Quarta legge di Maxwell
Per ottenere la quarta equazione di Maxwell dobbiamo introdurre il
concet 252d39c to di corrente di spostamento. Analizzando un circuito capacitivo
alimentato in alternata, possiamo notare che ad una variazione di tempo ![]() , corrisponde una variazione di tensione
, corrisponde una variazione di tensione ![]() A questa inoltre
corrisponde una variazione di campo elettrico
A questa inoltre
corrisponde una variazione di campo elettrico ![]() , a cui corrisponde a sua volta una variazione di carica
, a cui corrisponde a sua volta una variazione di carica ![]() . Partendo dalla legge
. Partendo dalla legge ![]() e ricordando che
e ricordando che ![]() e
e ![]() , possiamo facilmente giungere a
, possiamo facilmente giungere a 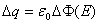 . Definendo
. Definendo ![]() come corrente di
spostamento considerando
come corrente di
spostamento considerando ![]() , possiamo riscrivere la legge di Ampere:
, possiamo riscrivere la legge di Ampere:
![]()
Le onde elettromagnetiche
Dalla combinazione delle quattro equazioni proposte Maxwell ottenne altre equazioni in funzione del tempo, dalla cui soluzione ottenne:
![]()
![]()
Egli concluse inoltre che campo magnetico ed elettrico oscillano in direzioni tra loro perpendicolari e la composizione di queste oscillazioni corrisponde ad un'onda, detta elettromagnetica, che si propaga con direzione perpendicolare al piano individuato dai vettori E e B con verso tale da formare con i due vettori una terna levogira. Possiamo osservare come, a differenza delle onde meccaniche, quelle magnetiche sono individuate da due equazioni e non da una soltanto.
Le onde elettromagnetiche emesse da un dipolo
I risultati teorici ottenuti da Maxwell si possono ben riscontrare nel funzionamento di un'antenna a dipolo, connessa ad un generatore di corrente alternata. Le cariche che si muovo nell'antenna creano un campo elettrico ondulatorio che si propaga alla velocità della luce e le linee del campo elettrico sono sempre perpendicolari alla direzione di propagazione: si dice infatti che l'onda del campo elettrico è un'onda trasversale. Un antenna percorsa da corrente genera però anche un campo magnetico, e poiché la corrente è alternata, anche il campo magnetico è oscillatorio. Inoltre anche il campo magnetico risulta trasversale. Da un'antenna a dipolo vengono quindi emessi un'onda di campo elettrico e una di campo magnetico perpendicolari tra loro e in fase e per gli studi di Maxwell ciò significa che si è in presenza di un'onda elettromagnetica.
La classificazione delle onde
L'insieme delle onde con tutte le possibili lunghezze d'onda viene chiamato spettro elettromagnetico. E' utile suddividere tale spettro in alcune categorie, anche se spesso tali categorie si sovrappongono, poiché esso si estende su un intervallo amplissimo di valori, pari a circa 20 ordini di grandezza.
Le onde radio: hanno in genere frequenza
inferiore a 109 Hz e lunghezza d'onda maggiore di
Le microonde: hanno lunghezza d'onda molto corta, da un millimetro sino a pochi centimetri. Sono i tipi di onde utilizzate dai radar, dalle trasmissioni telefoniche satellitari.
Le onde infrarosse: Hanno una frequenza di
circa 10-
La luce visibile: le lunghezze d'onda
rilevabili dall'occhio umano vanno da
Le onde ultraviolette: quando la frequenza aumenta e l'occhio non è più in grado di percepire le onde, si hanno le onde ultraviolette Quelle più vicine alla sensibilità dell'occhio vengono assorbite dall'ozono presente nella nostra atmosfera, mentre quelle più lontane si sovrappongono ai raggi X.
I raggi X: vengono generati bombardando con un fascio di elettroni una lamina metallica entro un tubo vuoto. Possono penetrare materiali morbidi, tra cui la carne. Una parte di raggi X si sovrappone a quelli gamma, ma differiscono per il modo in cui sono generate.
I raggi gamma: hanno lunghezze d'onda a volte paragonabili al nucleo di un atomo. Sono generati dalle variazioni di struttura di certi nuclei atomici (radioattività) e dai raggi cosmici dello spazio esterno.
La ricezione delle onde radio
E'
possibile rilevare un'onda elettromagnetica rilevando la sua parte elettrica o
la sua parte magnetica. Consideriamo la parte elettrica. Disponiamo un'antenna
lungo il cammino dell'onda elettrica. Quando questa colpisce l'antenna, mette
in moto le cariche al suo interno e poiché il campo è oscillatorio la polarità
nell'antenna verrà continuamente invertita, in modo che anche le cariche al suo
interno si muovano in modo oscillatorio creando una corrente alternata. Questa
corrente alternata, attraverso la mutua induzione, induce una tensione
alternata in un circuito RLC accoppiato all'antenna. Per poter ricevere il
segnale dell'onda, è necessario che il circuito RLC entri in risonanza con
l'onda. Ma poiché l'antenna è colpita da moltissime onde di diversa frequenza,
per selezionare quella che interessa, è necessario poter cambiare la frequenza
di risonanza del circuito RLC per sintonizzarsi. Ricordando che la frequenza di
risonanza in un circuito RLC è ![]() , basterà modificare
la capacità del condensatore per variare tale frequenza e selezionare l'onda da
cui ricevere il segnale.
, basterà modificare
la capacità del condensatore per variare tale frequenza e selezionare l'onda da
cui ricevere il segnale.
Come detto è possibile rilevare un'onda elettromagnetica anche dalla sua parte magnetica. Infatti l'onda elettromagnetica induce direttamente una f.e.m. oscillatoria in un circuito RLC, senza aver bisogno di un'antenna che crei in modo induttivo tale f.e.m. nel circuito. Il metodo di sintonizzazione risulta poi lo stesso in entrambi i casi.
Relazione tra campo magnetico e campo elettrico in un'onda elettromagnetica
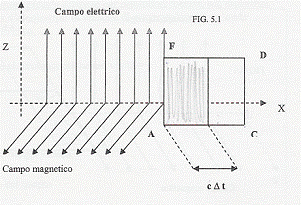 Consideriamo un'onda elettromagnetica che si
propaga nel vuoto e un rettangolo posto nel piano XZ attraversato dall'onda,
come mostrato in figura. Poiché FA=DC=h, avremo che l'area della zona
tratteggiata è
Consideriamo un'onda elettromagnetica che si
propaga nel vuoto e un rettangolo posto nel piano XZ attraversato dall'onda,
come mostrato in figura. Poiché FA=DC=h, avremo che l'area della zona
tratteggiata è![]() . Sappiamo che
. Sappiamo che ![]() ;
;
Sappiamo inoltre che il secondo termine dell'equazione è la forza elettromotrice indotta da un campo magnetico variabile.
![]()
Calcoliamo la circuitazione di E lungo i lati del rettangolo ACDF:
![]() perché il campo
elettrico e spostamento sono perpendicolari
perché il campo
elettrico e spostamento sono perpendicolari
![]() perché il fronte
d'onda non è ancora raggiunto il lato DC
perché il fronte
d'onda non è ancora raggiunto il lato DC
![]() .
.
Dunque avremo che ![]()
Sostituendo i valori ottenuti nella terza equazione di Maxwell otteniamo:
![]() , da cui
, da cui ![]() . Quest'ultima equazione, dove c è la velocità dell'onda
elettromagnetica nel vuoto, esprime la relazione tra campo magnetico e campo
elettrico.
. Quest'ultima equazione, dove c è la velocità dell'onda
elettromagnetica nel vuoto, esprime la relazione tra campo magnetico e campo
elettrico.
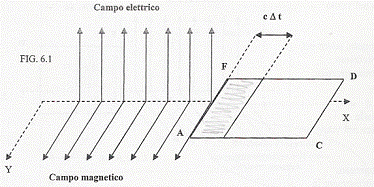 Velocità
delle onde elettromagnetiche nel vuoto
Velocità
delle onde elettromagnetiche nel vuoto
Consideriamo
un'onda elettromagnetica che si propaga nel vuoto e un rettangolo posto nel
piano XY, attraversato dall'onda, come mostrato in figura. Poiché AF=DC=h,
avremo che l'area della zona tratteggiata è![]() . Sappiamo che
. Sappiamo che ![]() poiché non vi è
presente corrente ohmica. Calcolando la circuitazione di B otterremo che
poiché non vi è
presente corrente ohmica. Calcolando la circuitazione di B otterremo che ![]() e calcolando la variazione di flusso di E che
e calcolando la variazione di flusso di E che ![]() . Sostituendo i valori ottenuti nella quarta equazione di
Maxwell, possiamo scrivere:
. Sostituendo i valori ottenuti nella quarta equazione di
Maxwell, possiamo scrivere: ![]() . Ricordando inoltre la relazione tra campo magnetico e campo
elettrico
. Ricordando inoltre la relazione tra campo magnetico e campo
elettrico ![]() , possiamo scrivere
, possiamo scrivere ![]() , da cui otteniamo che
, da cui otteniamo che ![]() . Sapendo che
. Sapendo che ![]() e che
e che ![]() , otteniamo che
, otteniamo che ![]() .
.
Velocità delle onde elettromagnetiche in un dielettrico
Come trovato la velocità di un'onda elettromagnetica nel vuoto è ![]() . Se vogliamo conoscere la velocità dell'onda in un
dielettrico, non possiamo considerare la permeabilità magnetica e la costante
dielettrica nel vuoto, ma avremo bisogno di valori assoluti, che si ottengono
moltiplicando i coefficienti considerati nel vuoto per quelli relativi al mezzo
in cui si propaga l'onda. Otterremo così che:
. Se vogliamo conoscere la velocità dell'onda in un
dielettrico, non possiamo considerare la permeabilità magnetica e la costante
dielettrica nel vuoto, ma avremo bisogno di valori assoluti, che si ottengono
moltiplicando i coefficienti considerati nel vuoto per quelli relativi al mezzo
in cui si propaga l'onda. Otterremo così che:
![]() .
.
Il termine ![]() , viene chiamato indice di rifrazione assoluto del mezzo in
cui si propaga l'onda elettromagnetica e viene indicato con la lettera n.
Dunque avremo che
, viene chiamato indice di rifrazione assoluto del mezzo in
cui si propaga l'onda elettromagnetica e viene indicato con la lettera n.
Dunque avremo che ![]()
Energia trasportata da un'onda elettromagnetica
L'energia trasportata da un'onda elettromagnetica è data dalla somma di energia associata al campo elettrico e quella associata al campo magnetico.
Possiamo calcolare l'energia associata al campo elettrico dallo studio
di un circuito capacitivo: ricordandosi che l'energia immagazzinata da un
condensatore è ![]() e che
e che ![]() e
e ![]() , possiamo calcolare la densità di energia associata al campo
elettrico:
, possiamo calcolare la densità di energia associata al campo
elettrico:
![]() , da cui otteniamo che
, da cui otteniamo che ![]() .
.
Possiamo calcolare l'energia associata al campo magnetico dallo studio di un circuito RL, ottenendo così (VEDI INDUZIONE ELETTROMAGNETICA) che:
![]()
Sommando dunque le energie associate ai due campi otterremo l'energia
trasportata dall'onda elettromagnetica per unità di area. Essa risulta: ![]() . Questo vettore prende il nome di vettore di Poyniting e ci
permette di affermare che l'energia trasportata per unità di area e per unità
di tempo da un'onda elettromagnetica, si propaga nella direzione e nel verso di
propagazione dell'onda stessa.
. Questo vettore prende il nome di vettore di Poyniting e ci
permette di affermare che l'energia trasportata per unità di area e per unità
di tempo da un'onda elettromagnetica, si propaga nella direzione e nel verso di
propagazione dell'onda stessa.
La legge dell'inverso del quadrato per la radiazione
Definiamo l'intensità di un'onda come ![]() , cioè la potenza che attraversa una superficie A.
Consideriamo adesso una sorgente puntiforme e isotropa, cioè che emette
radiazione con la stessa intensità in ogni direzione. Immaginiamo una
superficie sferica concentrica alla sorgente di raggio
, cioè la potenza che attraversa una superficie A.
Consideriamo adesso una sorgente puntiforme e isotropa, cioè che emette
radiazione con la stessa intensità in ogni direzione. Immaginiamo una
superficie sferica concentrica alla sorgente di raggio ![]() . Indicata con P la potenza della radiazione emessa,
otterremo che
. Indicata con P la potenza della radiazione emessa,
otterremo che ![]() . Se facciamo lo stesso procedimento con una nuova sfera di
raggio
. Se facciamo lo stesso procedimento con una nuova sfera di
raggio ![]() , avremo
, avremo ![]() . Mettendo insieme le due espressioni otterremo
. Mettendo insieme le due espressioni otterremo ![]() , che prende il nome di legge dell'inverso del quadrato per
l'energia irradiata da una sorgente puntiforme e che indica che l'intensità
della radiazione emessa da tale sorgente diminuisce con l'inverso del quadrato
della distanza dalla sorgente.
, che prende il nome di legge dell'inverso del quadrato per
l'energia irradiata da una sorgente puntiforme e che indica che l'intensità
della radiazione emessa da tale sorgente diminuisce con l'inverso del quadrato
della distanza dalla sorgente.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025