|
|
| |
MOTO ARMONICO SEMPLICE
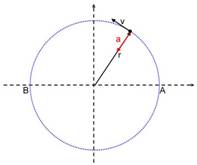 Riprendendo la teoria del
moto circolare uniforme, il quale è appunto il moto di un corpo che compie un
percorso circolare, è utile ricordare alcune formule relative all'argomento
Riprendendo la teoria del
moto circolare uniforme, il quale è appunto il moto di un corpo che compie un
percorso circolare, è utile ricordare alcune formule relative all'argomento
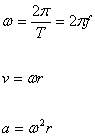
Partendo dal moto circolare, il moto armonico
semplice nasce dalla proiezio 959c22j ne di questo e di tutti gli elementi che vi anno
parte su uno dei diametri. Facendo questo, accade che a intervalli di tempo
uguali tra loro, il vettore posizione spazia un angolo sempre uguale (![]() ), ma non vale lo stesso per le proiezioni.
), ma non vale lo stesso per le proiezioni.
|
|
|
|
|
|
|
|
|
|
|
|
Dall'unione della legge oraria dello spazio e dell'accelerazione in funzione del tempo si ricava la relazione fondamentale del moto armonico.
![]()
Per far sì che il moto armonico semplice sia autonomo dal moto circolare uniforme, il raggio della circonferenza, che coincide con la massima elongazione, prende il nome di ampiezza (A); mentre la velocità angolare diventa pulsazione.
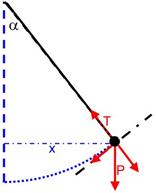 Nel moto del pendolo si
presenta un caso di moto armonico.
Nel moto del pendolo si
presenta un caso di moto armonico.
Infatti il peso del corpo appeso ha una componente che permette la traslazione su un arco di circonferenza; il valore di questo componente è pari a
![]()
Se l'angolo ![]() è molto piccolo, la
differenza tra la lunghezza della corda e quella dell'arco sotteso dall'angolo
precedente è minima e inoltre si può affermare che il componente della forza
peso è parallelo allo spostamento lineare del corpo.
è molto piccolo, la
differenza tra la lunghezza della corda e quella dell'arco sotteso dall'angolo
precedente è minima e inoltre si può affermare che il componente della forza
peso è parallelo allo spostamento lineare del corpo.
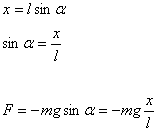
Infine comparando quest'ultima formula con il secondo principio della dinamica
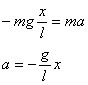
Quest'ultima è molto simile alla formula della relazione fondamentale del moto armonico.
Grazie a questa similitudine possiamo affermare che la pulsazione e le altre formule riguardanti il moto del pendolo sono
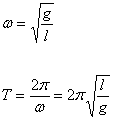
RISONANZA
Prendendo in considerazione un oscillatore elastico al quale è appesa una massa, la pulsazione del moto armonico che compie muovendosi è
![]()
Se all'oscillatore applichiamo una forza che nel corso del tempo cambia seguendo un moto armonico tutto suo con una pulsazione differente da quella dell'oscillatore elastico, questa può esser scritta come
![]()
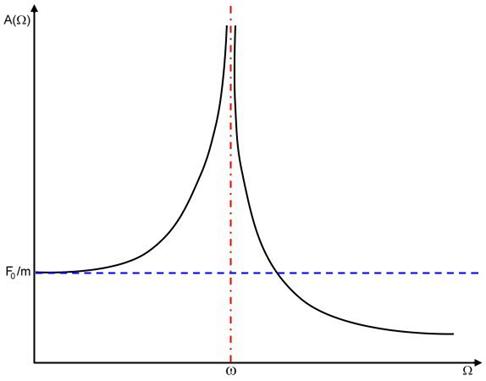
Sommando tutte le forze che agiscono su questo sistema, quindi la forza applicata e quella di richiamo della molla
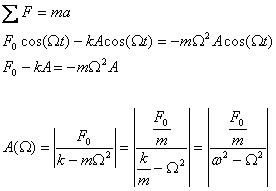
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025