|
|
| |
|
|
Un moto di particolare interesse dal punto di vista matematico-fisico è sicuramente quello armonico; per ipotizzarlo basti pensare ad un blocco di massa M, a cui è attaccata una molla ideale, di costante elastica k e priva di massa, vincolata a sua volta ad una parete: con tali ipotesi è possibile immaginare un moto periodico, causato da una forza di richiamo costante nel tempo (data in questo caso dalla legge di Hooke: F= - kx), che descrive un'oscillazione completa in un tempo detto Periodo (T).
L'analisi matematica di tale fenomeno si ottiene uguagliando la forza di richiamo alla forza data dalla seconda legge di Newton:
Ma = - kx a si può scrivere come ![]() , per cui
, per cui
M
![]() = - kx o ancora
meglio
= - kx o ancora
meglio ![]() +
+ ![]() x = 0
x = 0
Quest'ultima espressione rappresenta un equazione differenziale di secondo ordine, non omogenea, la cui soluzione "potrebbe essere" una funzione trigonometrica, che è caratterizzata dal fatto di avere la derivata seconda uguale, a meno di qualche fattore, alla funzione stessa.
Ipotizziamo, perciò, di avere x = xm cos(wt+Φ), e deriviamo:
![]() = - w xm sin (wt+ e
= - w xm sin (wt+ e
![]() = - w2 xm
cos (wt+
= - w2 xm
cos (wt+
Ritornando all'equazione differenziale, sostituiamo i valori ottenuti:
- w2
xm cos (wt+ ![]() xm
cos(wt+Φ)
xm
cos(wt+Φ)
da
cui otteniamo la relazione w2
= ![]() , o meglio w =
, o meglio w = ![]() , chiamata "frequenza
angolare" o "pulsazione". xm rappresenta l'ampiezza massima
dell'oscillazione; Φ invece è detta costante di fase, e rappresenta lo
"spostamento temporale" del moto.
, chiamata "frequenza
angolare" o "pulsazione". xm rappresenta l'ampiezza massima
dell'oscillazione; Φ invece è detta costante di fase, e rappresenta lo
"spostamento temporale" del moto.
w = 2π /T oppure w = 2 π ν dove ν è la frequenza, ovvero l'inverso del periodo ν = 1/T.
Invertendo tali relazioni otteniamo T = 2π/w
Sollecitazione che tende a far ruotare attorno al proprio asse di rotazione una parte di un oggetto, (ad esempio una barra), rispetto ad un'altra parte vincolata. L'entità della torsione è pari al prodotto della forza applicata per la distanza fra l'asse di rotazione dell'oggetto e il punto d'applicazione della forza stessa.
Se l'entità della torsione supera il limite d'elasticità del materiale, questo subisce una deformazione permanente, che può arrivare alla rottura.
|
|
Quando applichiamo delle forze ad un corpo, tale che la risultante di queste e dei momenti sia nulla, ci accorgiamo che tali azioni provocano nel corpo degli sforzi e delle deformazioni. Le molecole del corpo sottoposte agli sforzi, tendono a spostarsi dalla loro configurazione d'equilibrio ed esercitano un'azione diretta sulle molecole circostanti: in tal modo si avrà una distribuzione di sforzi in tutto il corpo. Il rapporto tra lo sforzo e la deformazione ci fornisce un coefficiente, che descrive la migliore o minore capacità del corpo di deformarsi. Tale coefficiente ha una natura tensoriale, in quanto deriva dalla combinazione di più componenti vettoriali (almeno nove vettori).
Consideriamo il comportamento elastico di un corpo solido sottoposto a torsione: data una sbarra omogenea di forma cilindrica, lunghezza l e raggio r, fissata per l'estremità superiore ad una superficie fissa. Applicando una coppia di forze, di momento M, si osserva una torsione, ovvero l'estremità libera ruota di un angolo θ, che soddisfa la relazione M = c θ ("c" è una costante di proporzionalità).
Ogni altra sezione
della sbarra situata alla distanza l' < l rispetto l'estremità fissa,
subisce una rotazione: ![]() ' =
' = ![]()
![]() .
.
|
|
La torsione è un caso particolare di scorrimento: infatti immaginiamo di considerare nell'intorno del cilindro uno strato cilindrico coassiale di raggi r e r+dr, e poi supponiamo di "segare" tale strato lungo una generatrice e di "stenderlo" su di un piano. In tale rappresentazione si spiega come la torsione si riduce ad una deformazione per scorrimento.
La sbarra in esame,
subendo una deformazione θ, ammette uno scorrimento α = ![]() . Questo valore di "scorrimento", per un materiale con modulo
di rigidità μ, richiede una forza "traente" pari a : F/S= μ
α = μ
. Questo valore di "scorrimento", per un materiale con modulo
di rigidità μ, richiede una forza "traente" pari a : F/S= μ
α = μ ![]() .
.
La forza
infinitesima che agisce sulla corona circolare considerata prima ( di raggi r e
r+dr), diventa dF/dS = μ ![]() , e siccome dS =
, e siccome dS = ![]()
![]()
![]() =
= ![]()
A questa forza corrisponde
un momento torcente dM = ![]() , che agisce sulla sbarra, cioè il cilindro di raggio R (per
non confondere la variabile d'integrazione):
, che agisce sulla sbarra, cioè il cilindro di raggio R (per
non confondere la variabile d'integrazione):
dM = ![]() →
→ ![]() →
→ ![]() , e chiamando nuovamente r il raggio della sbarra:
, e chiamando nuovamente r il raggio della sbarra: ![]()
Osservando ora la relazione precedente, M = c θ ci accorgiamo che c è uguale alla quantità
c = ![]() . Ponendo poi κ =
. Ponendo poi κ = ![]() da cui la forma delle
legge di Hooke M = c θ; da questa si può ancora ricavare
da cui la forma delle
legge di Hooke M = c θ; da questa si può ancora ricavare ![]() , dove κ prende il nome di modulo di torsione
, dove κ prende il nome di modulo di torsione
|
|
Il Pendolo di Torsione è un sistema che applica (nei limiti di varie approssimazioni), il moto armonico inizialmente esposto.
Consideriamo, ad esempio, una struttura costituita da un filo vincolato all'estremità superiore, mentre all'estremità inferiore è attaccato un corpo (disco omogeneo, cilindro omogeneo, sfera omogenea.); tale filo presenta un "coefficiente di proporzionalità di Hooke "c"; se sottoposto ad una piccola torsione, la fibra opporrà un momento di richiamo, proporzionale allo spostamento angolare θ; per cui la forza agente sarà : F = - c θ.
Il meno è giustificato dal fatto che l'azione è diretta in verso opposto al moto.
La formulazione rotazionale della seconda legge di Newton, per un sistema con asse fisso, è:
F = I![]() , dove I è il
momento d'inerzia del corpo posto in rotazione.
, dove I è il
momento d'inerzia del corpo posto in rotazione.
L'uguaglianza
tra le due espressioni ci fornisce l'equazione differenziale: ![]() +
+ ![]() θ = 0
θ = 0
La corrispondenza con l'equazione del moto armonico semplice ci fornisce immediatamente la soluzione:
w
= ![]() , che rappresenta la "pulsazione angolare": w =
, che rappresenta la "pulsazione angolare": w = ![]() , e invertendo:
, e invertendo:
T = ![]() =
= 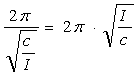 .
.
Tema della prova:
Determinare il modulo di torsione del filo di sospensione del pendolo con il metodo delle oscillazioni libere. [I Parte]
Misurare il momento d'inerzia di un corpo incognito con il pendolo torsione, avente lo stesso filo della parte I. [II Parte]
Materiale
Procedimento
I Parte
Consideriamo il filo di cui si vuole misurare il modulo di torsione: questo è fissato ad una estremità ad un supporto fisso, mentre l'altra è collegata (preferibilmente SALDATA) con un corpo di forma cilindrica. Sotto l'azione della forza peso il cilindro rimane sospeso in modo da poter compiere delle oscillazioni torsionali libere intorno ad un asse che coincide con la direzione del filo e passa per il punto di sospensione.
Il momento
d'inerzia del cilindro appeso all'asse intorno al quale si fanno compiere le
oscillazioni vale: I = 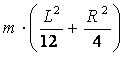 , dove R è il raggio del cilindro e L la sua lunghezza. [Teorema di Stainer]
, dove R è il raggio del cilindro e L la sua lunghezza. [Teorema di Stainer]
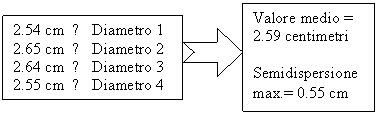
C'è da precisare che la misura del diametro viene fatta con il calibro a Coulisse, e vanno presi più valori, ognuno per un diverso diametro: il valore da considerare sarà il valore medio, mentre l'incertezza non sarà altro che la "semidispersione massima": la semidifferenza tra il valore massimo e il valore minimo delle misurazioni effettuate.
Applichiamo al corpo sospeso una coppia di forze, giacenti in un piano ortogonale alla direzione del filo; il momento generato provoca uno spostamento angolare, e quindi una torsione θ del filo.
Interrompendo l'azione di questa forza il filo esplica una "reazione elastica" che tende ad annullare la deformazione subita.
Tenendo conto delle
considerazioni già fatte a proposito del pendolo, sappiamo che w2 =![]() e
e
w2 = ![]() , c =
, c = 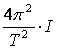 e che
e che ![]() si ottiene
si ottiene ![]()
Il periodo T delle
oscillazioni, per diminuire l'incertezza, si ricava sperimentalmente:
registrando il tempo t impiegato ad effettuare n oscillazioni complete, si
ha: T = t/n. Questo ragionamento deriva
dal fatto che in statistica lo scarto quadratico medio della media aritmetica è
minore di quello della variabile: ![]()
II Parte
Vogliamo misurare il momento d'inerzia di un corpo incognito, collegato a due fili, disposti verticalmente secondo lo stesso asse. Il filo è costituito dello stesso materiale usato per la determinazione del modulo di torsione κ.
Applicando al corpo una coppia di forze giacente su un piano ortogonale alla direzione del filo; il corpo ruota di un certo angolo, ed il filo subisce una torsione.
Indicando con I il
momento d'inerzia del corpo, il periodo d'oscillazione T = ![]() ,
,
w = 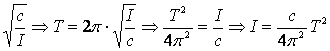
Poichè è già noto
il modulo di torsione κ, e nota la relazione c = ![]() , possiamo calcolare I:
, possiamo calcolare I:
I = ![]()
Dati sperimentali:
![]()
Il momento d'inerzia del cilindro può facilmente calcolarsi:
I
= ![]() 0.25
0.25![]() 22720.5
22720.5 ![]() 0.5 [grammi cm2]
0.5 [grammi cm2]
Il tempo entro cui il cilindro compie 15 oscillazioni è : 63.85 secondi, per cui il periodo da prendere in considerazione è T = 4.25 sec.
Per cui il coefficiente di torsione del filo sarà:
![]()
![]() [Parte I]
[Parte I]
Passando al secondo sistema, dobbiamo considerare soltanto il tempo impiegato a compiere 15 oscillazioni, mentre conosciamo già tutto il resto (coefficiente di torsione, raggio, lunghezza, π.)
Il tempo trascorso in 15 oscillazioni è 84.28 secondi, e da ciò si stima che un periodo T è pari a 5.61 secondi. Dalla formula possiamo ottenere il valore del momento d'inerzia del "corpo composto":
I = 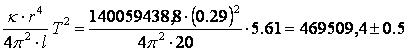
![]() [Parte II]
[Parte II]
Emanuele Umberto
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025