1) In relazione al II principio della Dinamica

fisica

In relazione al II principio della Dinamica si discuta la differenza tra forze reali e forze fittizie.

Calcolare la minima velocità con cui deve essere spinto il carrello mostrato in figura affinchè riesca a compiere il giro della morte. Il carrello parte dal punt 525i83f o A posto ad una altezza pari ad R e il raggio della guida circolare è R=5m.    

Sapendo che un corpo di massa m = 10 Kg, appoggiato su un tappeto elastico, produce una deformazione pari a 5 cm, calcolare la costante elastica della molla. Supponiamo che un bambino di massa M = 25Kg  si lasci cadere su tale tappeto elastico da una altezza h producendo una deformazione pari a 50 cm. Calcolare l'altezza da cui si è lanciato il bambino.

Due masse m₁ ed m₂, sono collegate da un filo in estensibile che scorre su un piolo fisso come rappresentato in figura.

a) Trovare l'accelerazione del sistema e la tensione del filo.

b) Se sul piano è presente un attrito con coefficiente μ, quale sarà l'accelerazione del sistema?

m₁=10 kg , m₂ = 4 kg,

Soluzioni

B

Esercizio 2

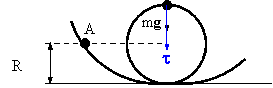
La condizione di distacco del carrello dalla guida si realizza quando la reazione vincolare nel punto B si annulla. Pertanto calcoliamo la reazione vincolare in B, t_B, applicando il secondo principio della dinamica:

Imponendo che la reazione vincolare si annulli, otteniamo la velocità minima in B :

   

Applicando il teorema della conservazione dell'energia tra i punti A e B :

ricavo la velocità minima che deve essere applicata in A per consentire al carrello di compiere il giro della morte:

Esercizio 3

Il tappeto elastico può essere schematizzato da una molla di costante elastica k

a) La costante elastica della molla si ricava imponendo la condizione di equilibrio statico tra la forza peso mg e la forza elastica di richiamo:

mg=kx

da cui si ricava  .

b) Applichiamo la conservazione dell'energia tra il punto A da cui si lancia il bambino e il punto B corrispondente alla posizione di equilibrio della molla:

e tra il punto B e il punto C di massima compressione

Dx

della molla, nell'ipotesi che la deformazione Dx=50cm

sia trascurabile rispetto ad h:

In questa approssimazione si ricava 

Notiamo che la deformazione Dx non è in realtà trascurabile rispetto ad h, pertanto nella seconda equazione occorre tenere in considerazione anche la variazione di energia potenziale gravitazionale:

da cui si ottiene

Esercizio 4

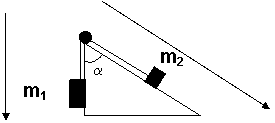
A)    Applicando la 2° equazione della dinamica ai due corpi separatamente, si ottiene il seguente sistema di equazioni in 2 incognite (T ed a):

m₁a = m₁g - T

-m₂a = -T + m₂gcosa

Dalla prima eq. Si ricava T = m₁g - m₁a che sostituita nella seconda eq. dà:

(m₁ + m₂) a = m₁g - m₂gcosa

da cui

a = g (m₁- m₂ cosa)/(m₁ + m₂) = 4,6 m/s²

T = 52.3 N

B) Analogamente al primo quesito ed aggiungendo il termine dovuto all' attrito nella seconda equazione si ha:

m₁a = m₁g - T

-m₂a = -T + m₂gcosa + m m₂gsena

Ricavando  T dalla prima eq. e sostituendola nella seconda si ha:

a = g (m₁ - m₂cosa m m₂sena)/(m₁ + m₂) = 4,2 m/s²