Sintesi Vettori
I vettori sono gli oggetti matematici che costituiscono la base di tutte le
teorie fisiche.
Esponiamo qui i concetti fondamentali della teoria dei vettori limitatamente al
caso dei vettori dello
spazio (tridimensionale) della nostra esperienza (ed in
particolare del piano (bidimensionale))
tenendo presente che tali concetti possono essere estesi a spazi a più
dimensioni ed addirittura a
spazi astratti formati oggetti astratti quali le funzioni.
Tali estensioni vengono approfondite in altre pagine di questo sito.
Un vettore si può rappresentare come un segmento dotato di una freccia.
Un generico vettore V dello spazio ha 3 componenti
rispetto ad un sistema di coordinate
cartesiane ortogonali ed è indicato come 
.
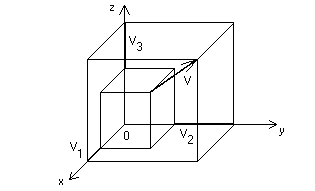
Seguendo l'usuale formalismo degli indici, possiamo inoltre indicare il
vettore V tramite le sue
componenti, ovvero useremo indipendentemente V e 
per esprimere il vettore stesso (l'indice
i assume i valori interi 1, 2 , 3 ).
Ribadiamo ulteriormente il significato di componente di un vettore rispetto ad
un sistema di coordinate
cartesiane tramite il seguente esempio nel piano :
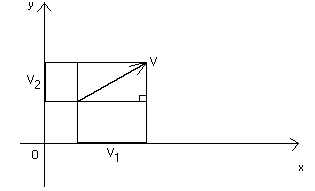
dove il vettore V può essere "applicato" in qualunque
punto.
Un vettore possiede un modulo o intensità (o norma ) che ne
rappresenta la lunghezza definibile
tramite il teorema di Pitagora. Il modulo del vettore V è
indicato con |V| e vale :
nello spazio
e :
nel piano.
01 - Operazioni elementari.
Esiste il vettore nullo le cui componenti sono tutte nulle e che ha
perciò modulo 0 . Esso coincide
con l'origine 0 del sistema di assi cartesiani. Esso è :
0 = (0 , 0 , 0)
e per ogni vettore V esiste il vettore inverso
-V ottenuto moltiplicando per -1 tutte le sue
componenti per cui :
.
Il vettore inverso di un vettore dato è quel vettore di uguale direzione,
intensità ma di verso opposto.
Dati i due vettori A e B , si definisce per addizione
l'operazione che fa ottenere come risultato il
vettore C = A + B le cui componenti sono date dalla somma
delle corrispondenti componenti :
dove i = 1, 2, 3 .
L'addizione fra due vettori ha una importante interpretazione grafica che va
sotto il nome di regola
del parallelogramma. Nel piano :
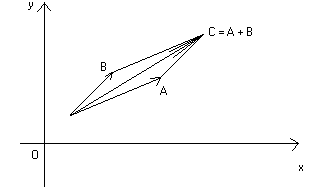
Questa regola corrisponde in fisica alla legge di composizione delle forze.
Dati uno scalare (numero reale) k ed un vettore A , si
definisce la moltiplicazione per uno scalare
come l'operazione che fa ottenere per risultato il vettore B = k A
le cui componenti sono date dal
prodotto di k per le corrispondenti componenti di A :
dove i = 1, 2, 3 .
Moltiplicando un vettore per k si ottiene un altro vettore di
uguale direzione, intensità moltiplicata
per |k| e stesso verso, se k è positivo, o verso
opposto, se k è negativo.
Ovviamente, moltiplicando un vettore per -1 si ottiene il vettore
inverso e moltiplicando un vettore
per 0 si ottiene il vettore nullo.
02 - Prodotto scalare.
Fra due vettori A e B è possibile definire due tipi di
moltiplicazione : quella scalare, che dà come
risultato uno scalare, e quella vettoriale, che dà come risultato un vettore.
Di queste presentiamo qui la prima, il cosiddetto prodotto scalare.
Il prodotto scalare (o prodotto interno) fra due vettori è definito come
la somma dei prodotti delle
componenti corrispondenti ed è indicato con il simbolo · ,
ovvero :
.
Sottolineiamo il fatto che il risultato 
del
prodotto scalare è uno scalare (cioè un numero).
Il prodotto scalare assume l'importante significato geometrico di essere uguale
al prodotto del modulo
del primo vettore per la proiezione dell'altro vettore sulla direzione su cui
giace il primo.
Graficamente, nel piano :
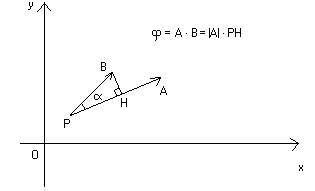
Una tipica applicazione fisica del prodotto scalare è il lavoro. Quando
una forza subisce uno
spostamento vi è lavoro ed il suo valore è appunto dato dal prodotto scalare
fra il vettore
forza per il vettore spostamento.
