INFtub.com è un sito progettato per cercare i documenti in vari tipi di file e il caricamento di articoli online.

Prima pagina Caricare document Cerca documento Contatto

  Moto uniforme e moto uniformemente accelerato

Materiali

Carrello

1 Peso

filo

Rotaia anti attrito ad aria

Piattaforma di arresto del peso.

Compressore

Strumenti

Scala graduata (valore max. 2,5 m.- errore 1 mm.)

Cronometro con contatti di Avvio e Stop (errore 1 centesimo di secondo)

^Teoria   

Abbiamo cosi' due tipi di esperimenti: in uno misuriamo la velocità media , e in un altro l ' accelerazione costante.

Il moto uniforme si ha quando le misurazioni eseguite sono direttamente proporzionali al tempo percorso. Per verificarne la velocità dovremo calcolare il rapporto delle distanze e i tempi. Il rapporto risulterà pressoché costante.

Questo tipo di movimento può essere visualizzato per mezzo di una formula. Indicando con s la distanza e con t il tempo.

Perciò v sarà la velocità del moto uniforme. Nel Sistema Internazionale l ' unità di misura e' il metro per secondo (m/s) .Essendo questa una misurazione derivata il suo errore sarà la somma degli errori da cui e' derivata (es. err. spazio percorso = err. Partenza + err. Arrivo ), però noi non considereremo gli errori relativi per la loro grandezza .

Il moto uniformemente accelerato.

Proviamo ora a sottoporre al carrello una forza non equilibrata. In questo caso il carrello viene costantemente trascinato con una forza costante. Vedremo subito che il moto del carrello non e' uniforme : la velocità aumenta proporzionalmente al tempo. Si può esprimere questo fatto con una formula:

Il rapporto tra velocità e tempo si definisce accelerazione e ci dice di quanto varia la velocità del carrello.

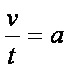
La sua unità di misura e' il metro al secondo quadrato (m/s2).    Con questo possiamo affermare che un corpo soggetto ad una forza costante ha un accelerazione costante. Ciò ci conferma che una forza non produce velocità ma variazioni di velocità.

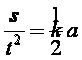
Inoltre vediamo che le distanze percorse sono direttamente proporzionali ai quadrati dei tempi: Si può notare che la costante k corrisponde alla meta' di a. In formula:   

^{Metodo Operativo}

Prima esperienza

Per prima cosa abbiamo montato la rotaia, la abbiamo livellata e abbiamo montato il carrellino con il filo, il peso e la piattaforma di arresto. Poi abbiamo posizionato i contatti del cronometro badando che il peso tocchi la piattaforma prima che si apra il contatto di avvio.

Per motivi di scarsità di materiale abbiamo dovuto prima accendere il compressore e poi l ' orologio per evitare che le vibrazioni facessero partire l ' orologio. Lo sgancio del carrello avverrà per mezzo di una matita per non influenzare le misure. Lasciando il carrello libero di muoversi sotto l ' azione del peso  misuriamo il tempo misurato dal cronometro. Possiamo ora compilare una tabella.

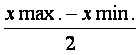
Con questi dati possiamo derivare anche la semi oscillazione massima con la formula:

In questo caso il risultato è 0,01.

Seconda esperienza

Il metodo operativo rimane sempre lo stesso ma evitiamo di posizionare la piattaforma di arresto.

La tabella è la seguente:

La media delle accelerazioni e' di 0.04 m/s2

La sua semi oscillazione massima è di 0.33

^Conclusioni

Nella prima esperienza

Abbiamo notato che la relazione tra le distanze percorse e il tempo impiegato per percorrerle è sempre uguale. Perciò il carrello dopo aver avuto una spinta iniziale ha proseguito con una velocità' costante .

Nella seconda esperienza

Osserviamo che la accelerazione di un corpo e' determinata da una forza costante.