|
|
| |
ELETTRONI ITINERANTI IN UN RETICOLO
Consideriamo un semplice modello per la conduzione elettrica in solidi cristallini. Un numero Ne di elettroni che "saltellano" tra stati associati a gli N siti di un reticolo regolare. Indichiamo con cis ,cis gli operatori che rispettivamente creano e distruggono elettroni nello stato associato al sito i e allo stato s della componente sz dello Spin . Per effetto della natura fermionica delle particelle valgono le seguenti regole di commutazione.
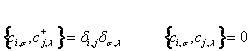 Eq.(1)
Eq.(1)
L'Hamiltoniana del sistema si esprime
![]() Eq.(2)
Eq.(2)
La somma tra parentesi angolari sugli indici i,j in Eq.(2) si estende per ogni i sui j che individuano i siti primi vicini del sito i (siti posti a distanza minima dal sito considerato . Il numero dei primi vicini varia a seconda del reticolo considerato). Ad esempio su di un reticolo unidimensionale (D=1) costituito da siti disposti a distanza a su di una retta abbiamo due primi vicini j=i+1,i-1. In reticolo bidimensionale (D=2) il numero dei primi vicini varia a se 555j92f conda della geometria del reticolo. Il minimo numero di primi vicini si ha quando il reticolo si ottiene dalla ripetizione nel piano di una cella elementare costituita da un quadrato di lato a. In tal caso il numero di primi vicini è pari a quattro. Analogamente per un reticolo tridimensionale (D=3) avremo sei primi vicini. Nella Hamiltoniana di Eq.(2) il primo termine rappresenta l' energia che deriva dal trasferimento di particelle da un sito ai siti adiacentied il secondo termine l'energia associata alla presenza della particella nel sito.
La costante t è legata all'ampiezza di probabilità associata al fenomeno di tunneling di particelle tra stati localizzati su siti adiacenti e separati da una barriera di energia potenziale.
Per capire l'origine fisica del modello
consideriamo una particella in un campo di energia potenziale simmetrico
costituito da due minimi separati da una barriera di potenziale. Ai due
minimi associamo un potenziale armonico
, il relativo stato fondamentale ci dà
una stima della incertezza sulla localizzazione della particella nello
stato relativo ad uno dei minimi. Se l'ampiezza
della barriera è molto maggiore di tale incertezza caratteristica si ottiene
una valutazione accurata dello stato fondamentale e del primo stato eccitato
costruendo due stati variazionali come
combinazioni rispettivamente simmetrica ed antisimmetrica degli stati
fondamentali ![]() relativi ai due
minimi. Tali stati e le loro energie
sono quelle previste dalla versione a due siti della Hamiltoniana di Eq.(2) se
l'ampiezza di trasferimento t è identificata con l'integrale di sovrapposizione
ed e con
l'energia media per lo stato di sito.
relativi ai due
minimi. Tali stati e le loro energie
sono quelle previste dalla versione a due siti della Hamiltoniana di Eq.(2) se
l'ampiezza di trasferimento t è identificata con l'integrale di sovrapposizione
ed e con
l'energia media per lo stato di sito.
![]() Eq.(3)
Eq.(3)
![]()
Abbiamo evidenziato un segno negativo perchè ci si aspetta che il trasferimento di particelle tra stati localizzati diminuisca l'energia del sistema. Questa ipotesi è compatibile con la formulazione variazionale solo se il potenziale armonico associati ai minimi supera la barriera di potenziale intermedia. Ciò si può ottenere facilmente diagonalizzando la vesione a due siti dell'Hamiltoniana di Eq.(2) con la seguente trasformazione canonica;
![]() Eq.(4)
Eq.(4)
![]()
![]()
Gli autovalori dell'energia risultano e e-t, e e+t . Queste energie sono le energie sono quelle che il metodo variazionale assegna agli stati combin azioni simmetrica o antisimmetrica
Nel caso di più siti la diagonalizzazione si ottiene passando al cosiddetto reticolo reciproco.
Il reticolo reciproco definisce una particolare trasformata di Fourier per ogni funzione definita sul reticolo.
![]() Eq.(5)
Eq.(5)
In Eq.(5) abbiamo introdotto una trasformazione dallo spazio dei siti,individuato dalle variabili l, ad un nuovo spazio detto del reticolo reciproco individuato dalle variabili q, fq è l'ampiezza di Fourier associata alla fi.. I possibili valori della variabile q vengono fissati dalle cosiddette condizioni al contorno. Nel caso di un numero elevato di siti i risultati non dipendono apprezzabilmente dal tipo di condizione al contorno ed è pertanto conveniente scegliere le condizioni più semplici ovvero le " condizioni periodiche al contorno" . Tali condizioni per un reticolo unidimensionale implicano che fN=f0 . Si può interpretare la condizione periodica in D=1 pensando che gli N siti siano disposti lungo una circonferenza in modo che il sito l=0 coincida con il sito l=N. Analoghe condizioni valgono per reticoli in D=2,3. In tali reticoli la posizione di un sito è individuata da un vettore n di componenti ni con i=1,2,3 rispettivamente in una ,due,tre,dimensioni. I numeri interi ni sono compresi tra zero ed Ni.Il numero totale dei siti N è il prodotto degli Ni. La periodicità si realizza spostandosi lungo ciascuna delle direzioni indipendenti rispetivamente dopo N1 o N2 o N3 passi reticolari. In tal caso sia l che q ed m in Eq.(5) indicano un vettore di due o tre componenti rispettivamente in D=2,3 la somma diventa una somma sui possibili valori delle componenti di q , il prodotto ql un prodotto scalare ed N il prodotto degli Ni. Dalle condizioni di periodicità otteniamo
![]() Eq.(6)
Eq.(6)
In Eq.(6) mi sono numeri interi positivi o negativi. Lo spazio definito dalle q è detto reticolo reciproco. Per avere lo stesso numero di gradi di libertà per il sistema nella rappresentazione del reticolo reciproco limitamo mi ai valori compresi tra +(Ni-1) /2 e -(Ni-1) /2. La scelta di valori di q simmetrici rispetto all'origine ci permette di ottenere che la trasformata nel reticolo reciproco della complessa coniugata di una funzione fl è la complessa coniugata della trasformata fq della funzione calcolata in -q . Si noti come il reticolo reciproco abbia lo stesso numero di punti del reticolo originale con spaziatura 2p/a invece di a.
La corrispondenza tra i due reticoli si può invertire, è possibile cioè definire la trasformazione opposta.
![]() Eq.(7)
Eq.(7)
Infatti è semplice dimostrare la validità delle seguenti relazioni.
![]()
![]() Eq.(8)
Eq.(8)
La trasformazione di Eq.(5) può essere applicata agli operatori di creazione e distruzione.
![]() Eq.(9)
Eq.(9)
E' importante verificare che i nuovi operatori definiti nel reticolo reciproco soddisfano le stesse regole di commutazione degli operatori originali. La trasformazione tra i due reticoli è pertanto una trasformazione canonica.
L'Hamiltoniana trasformata risulta inoltre diagonale.
![]() Eq.(10)
Eq.(10)
![]()
Si noti come un autostato sia ad esempio lo stato in cui si aggiunge al vuoto una particella nello stato q,s di energia eq
![]() Eq.(10)
Eq.(10)
Tale stato in virtù della Eq.(9) si esprime come stato sovrapposizione di stati localizzati sui siti del reticolo originale. Il modulo quadro dell'ampiezza di probabilità di osservare l'elettrone localizzato in un sito particolare risulta inoltre indipendente dal sito e pari ad 1/(N-1). In altre parole l'effetto tunnel ha portato la particella in uno stato stazionario completamente delocalizzato su tutto il reticolo. L'insieme delle eq costituisce la "banda di energia".
Si usa riassumere il risultato dicendo che la perturbazione dovuta all'effetto tunnel ha trasformato lo stato N volte degenere associato ad una particella localizzata in uno qualsiasi dei siti (la degenerazione è dovuta al fatto che l'energia è indipendente dalla scelta del sito) negli N stati distinti in energia che costituiscono la banda.
Lo stato fondamentale del sistema di Ne (minore di 2N) particelle si otterrà, in accordo col principio di Pauli, saturando progressivamente gli stati q (ogni stato q potrà accogliere al più due particelle in stato di spin opposto) fino ad una energia massima ef detta energia di Fermi.
Per studiare le proprietà di conduzione introduciamo un campo esterno il cui effetto sia quello di aumentare l'ampiezza di trasferimento in una direzione associata al verso positivo rispetto a quella associata al verso negativo. Se consideriamo , per semplicità un reticolo unidimensionale la nuova Hamiltoniana è la seguente.
![]() Eq.(10)
Eq.(10)
Si noti come le ampiezze di trasferimento t e ![]() associate rispettivamente
al trasferimento di particelle verso sinistra e destra debbano necessariamente
essere l'una la complessa coniugata dell'altra affinché l'operatore H risulti
hermitiano.
associate rispettivamente
al trasferimento di particelle verso sinistra e destra debbano necessariamente
essere l'una la complessa coniugata dell'altra affinché l'operatore H risulti
hermitiano.
La corrente si definisce naturalmente come il flusso di particelle trasferite nel verso positivo (a destra di i) meno quello associato al verso negativo.
![]() Eq.(11)
Eq.(11)
Passando al reticolo reciproco H risulta ancora diagonale ma l'energia eq non è più una funzione simmetrica della variabile q: i modi corrispondenti a q positivi avranno energia superiore ai modi con q negativi.
![]() Eq.(12)
Eq.(12)
Se il numero di elettroni Ne è minore del numero di stati moltiplicato per la degenerazione, nel caso cioè di banda non completamente piena, ciò comporta che,nello stato fondamentale, un maggior numero di elettroni si collocherà negli stati con q negativo dando luogo in base alla Eq.(11) ad una corrente media diversa da zero.
Nel caso invece di una banda completamente piena non è possibile trasferire elettroni su altri stati in quanto tutti gli stati sono completamente occupati. In questo caso nonostante all'applicazione del campo esterno non corrisponde lo stabilirsi di una corrente. Questi due diversi comportamenti corrispondono a quelli dei conduttori e degli isolanti.
Tali proprietà si ritrovano anche nel caso di un sistema in equilibrio termodinamico con un termostato a temperatura T. Utilizzando l'ensemble gran canonico otteniamo che l'occupazione media del modo q è data dalla formula caratteristica della statistica di Fermi-Dyrac.
![]() Eq.(13)
Eq.(13)
Il potenziale chimico corrisponde alla cosidetta "energia di Fermi" infatti a bassa temperatura l'occupazione data dall'Eq.(12) è molto prossima ad uno per eq minore di m e prossima a zero per eq maggiore di m. Tale andamento diventa discontinuo (o zero o uno) a temperatura nulla.
La corrente media a temperatura non nulla si ottiene dalla Eq.(11) pasando al reticolo reciproco, sostituendo i numeri medi di occupazione di Eq.(13) e le energie di banda in presenza di "hopping" anisotropo di Eq.(12).
![]() Eq.(14).
Eq.(14).
Si ottiene una corrente diversa da zero a temperatura non nulla anche nel caso di banda completamente piena. Tale corrente è dovuta al raccordo continuo che si ha a temperatura non nulla nella funzione di Fermi tra i valori asintotici 0,1. Tale effetto è peraltro molto piccolo anche a temperature relativamente elevate.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024