1. Introduzione

I. Un gioco è caratterizzato da regole che lo governano, dal numero di giocatori, dalle strategie a disposizione di ciascuno giocatore e dagli esiti (payoff) associati ad ogni combinazione di strategie giocabili.

II. Gioco: qualsiasi situazione in cui più giocatori si trovano a controllare ciascuno una o più variabili che influiscono sull'utilità propria e/o degli altri descrive l'interazione strategica nelle scelte di giocatori autonomi.

III. L'obiettivo di un giocatore consiste nella massimizzazione del proprio esito finale. Inoltre, ogni giocatore sa che anche gli altri perseguono il medesimo obiettivo. Questo conduce la concetto di razionalità massimizzante, tipicamente neoclassico, esplicitamente usato dalla teoria dei giochi.

IV. L'interazione strategica tra individui, sulla base delle norme dettate dalla loro razionalità, produce, quando esiste, l'equilibrio del gioco, che può non essere unico.

a. Un equilibrio è definibile come la combinazione delle migliori strategie a disposizione di ognuno degli agenti che prendono parte del gioco.

b. Il concetto di equilibrio è, quindi, distinto da quello di esito del gioco, quest'ultimo identificato nell'insieme dei payoff prodotti dalle strategie di equilibrio.

2. Classificazione dei giochi, definizione e rappresentazione

a)    Giochi cooperativi e giochi non cooperativi

I. Giochi non cooperativi sono quelli in cui non sono fattibili accordi vincolanti tra giocatori

II. Giochi cooperativi in cui tali accordi sono fattibili per certi sottoinsiemi di giocatori (detti coalizioni ammissibili). Esempio di gioco pienamente cooperativo: cartello di imprese.

b)   Per i giochi non cooperativi escludiamo che:

III. Possano esservi contrattazioni preliminari a carattere vincolante (gioco pienamente cooperativo);

IV. Possano esservi pagamenti collaterali tra giocatori (gioco parzialmente cooperativo).

c)    Per i giochi non cooperativi diremo:

V. Che è un gioco a somma costante se il payoff  complessivo a disposizione degli agenti non varia al variare delle loro scelte: il guadagno di uno è la perdita dell'altro. Nel caso contrario diciamo che il gioco è a somma variabile.

VI. Che il gioco è ad informazione perfetta, se ogni giocatore, in ogni istante del gioco, è interamente a conoscenza della sua storia passata; vale a dire dell'intera sequenza di mosse effettuate da lui e dagli altri fino a quel momento.

VII. Che il gioco è ad informazione simmetrica, se nessuno dei giocatori dispone di informazioni di cui non siano in possesso anche tutti gli altri.

VIII. Che il gioco è ad informazione completa, se gli elementi che lo caratterizzano sono di comune conoscenza tra tutti i giocatori. Altrimenti si dice che il gioco è con informazione incompleta.

Rappresentazione del gioco in forma strategica

Un gioco in forma strategica con due giocatori si rappresenta comunemente mediante una bimatrice le cui righe e colonne sono intestate rispettivamente alle strategie pure del giocatore 1 e del giocatore 2. In corrispondenza alla riga k e alla colonna j , la bimatrice riporta la coppia di vincite associata alla combinazione strategica (k,j). Per brevità, se la bimatrice ha dimensione mxn, si parla di gioco mxn. Ad esempio , la bimatrice G=

rappresenta un generico gioco 2x2.

Definizione 2.1

Un gioco in forma strategica è caratterizzato da tre elementi:

i. un insieme di N giocatori;

ii. un insieme Si di strategie pure per ogni giocatore ;

iii. una funzione di vincita per ogni giocatore .

G.1 - gioco in forma strategica:

N=2 ,

Strategie: Paese1:;

Paese2: ;

4 possibili esiti:     (guerra, guerra); (pace, guerra)

(guerra, pace); (pace , pace)

Il numero in alto a sin in ciascuna cella individua la vincita per il giocatore riga; il numero in basso a destra, la vincita per il giocatore colonna.

Definizione 2.2

Un gioco in forma estesa è caratterizzato da sette elementi:

un insieme di giocatori tra i quali può rientrare la Natura;

un albero di gioco i cui nodi denotano situazioni strategiche;

un'attribuzione dei nodi ai giocatori che specifica a chi è intestato ciascun nodo;

una lista di insiemi di informazione che indica quali nodi un giocatore può scegliere in ogni suo insieme di informazione;

un elenco di mosse o azioni che ciascun giocatore può scegliere in ogni suo insieme si informazione;

una funzione di vincita per ogni giocatore (esclusa al più la Natura);

una distribuzione iniziale di probabilità sulle azioni della Natura.

Rappresentazione del gioco in forma estesa

Ogni gioco in forma estesa ammette una rappresentazione in forma strategica che è unica a meno di permutazioni dell'ordine dei giocatori e delle loro strategie. Al contrario, in generale, un gioco in forma strategica ammette più rappresentazioni in forma estesa.

		a1					a2
								b2
	b1

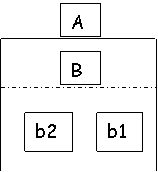
(m,n)    (p,q) (r,s) (w,z)

La presenza di un legame tra più nodi in forma tratteggiata evidenzia il fatto che il giocatore in questione non sa con esattezza in quale nodo si trova. Se invece il set informativo comprende un solo nodo, il gioco è ad informazione perfetta.

Indichiamo come supergioco l'intera struttura ad albero. Definiamo come sottogioco (proprio) ciascun sottoinsieme del supergioco avente origine in un nodo singolo e contenente tutti i nodi successivi a quello di origine.

In forma estesa: ad ogni profilo di strategie corrisponde non un esito, ma una distribuzione di probabilità sugli esiti e sui vettori di vincita. Tali vettori sono espressi in unità di utilità.

Le strategie pure e le strategie miste

Strategie Pure. Indichiamo con una generica strategia pura del giocatore i e con una generica combinazione di strategie pure dei suoi avversari, e con una generica combinazione di strategie pure. Sostituendo a indichiamo i corrispondenti insiemi. Ad esempio, rappresenta l'insieme delle combinazioni di strategie pure degli avversari di i.

Strategie miste. Sostituendo a nella precedente definizione di strategia pura, riferiamo lo stesso concetto ad una strategia mista. Ad esempio, rappresenta una generica strategia mista del giocatore i. Analogamente, sostituendo a S indichiamo i corrispondenti insiemi nel caso di strategie miste. Ad esempio rappresenta l'insieme di tutte le combinazioni di strategie miste del gioco. Si ricordi che una strategia mista è una distribuzione di probabilità sulle strategie pure. Scriveremo 1/3A2/3B per indicare la strategia mista che attribuisce probabilità 1/3 alla strategia pura A e 2/3 alla strategia pura B (e 0 alla strategia pura C). Con una notazione alternativa scriveremo che per indicare che la strategia assegna la probabilità ½ alla strategia pura .

Giochi in forma strategica a somma variabile: alcuni criteri di soluzione

Dato il gioco in forma strategica o estesa, come si comporteranno i giocatori? Quali strategie sceglieranno?

Le ipotesi sui giocatori sono:

a)       che conoscano il gioco in cui sono immersi, che sappiano che gli altri partecipanti lo conoscono.

b)       Che siano razionali, che sappiano di esserlo, sappiano di saperlo e che ciò sia a conoscenza di tutti i giocatori.

Soluzione di un gioco non cooperativo: consiste nell'indicazione di un profilo di strategie come candidato per l'adozione da parte di giocatori nell'ipotesi a) e b).

Questo comporta possedere un criterio che permette di associare ad ogni gioco di una certa classe un profilo di strategie che i giocatori tenderanno a scegliere.

Essendo tale scelta del criterio basata su teorie del comportamento che fanno riferimento all'ipotesi di comportamento razionale, la soluzione che ne deriva è suscettibile di doppia interpretazione:

aspetto normativo: indica ai giocatori come essi dovrebbero giocare se accettassero certi principi di comportamento

aspetto predittivo: indica come andranno le cose (cosa faranno i giocatori) date le ipotesi.

Razionalità nella teoria dei giochi. Ogni giocatore si comporta in modo da ottenere il meglio per sè; sa che anche l'avversario si comporta in modo analogo ed è quindi in grado di valutare sia le proprie che le altrui scelte. Possiamo dire che il criterio di scelta segue un ragionamento del tipo: "io so che tu sai che io so che tu sai che...". In altre parole i giocatori risolvono un problema di ottimo, vincolato al fatto che anche gli avversari perseguano un ottimo vincolato.

Il criterio della dominanza

Una strategia h è dominante su tutte le altre possibili strategie a disposizione del giocatore, quando il risultato associato a h è sempre il migliore, quale che sia la mossa dell'avversario.

Se il giocatore è razionale e se tra le sue strategie ve ne è una strettamente dominante, possiamo esser certi che la sceglierà.

G.2 - dominanza

Giocatore A a₁ domina a₂; Giocatore B: b₂ domina b₁

Definizione 3.1 - Dominanza

Una strategia pura domina un'altra strategia pura se per ogni in . La definizione si estende in modo ovvio alle strategie miste.

Nel gioco G.1 la strategia "Guerra" è una strategia dominante per il giocatore 1 (verificate che =Guerra soddisfa la definizione di strategia dominante). Nel gioco G.2

Definizione 3.2 - Dominanza debole

Una strategia pura domina debolmente un'altra strategia pura se per ogni in e per almeno un s_i vale il segno di disuguaglianza stretta. La definizione si estende in modo ovvio alle strategie miste.

Una strategia pura è (debolmente) dominante se domina (debolmente) tutte le altre strategie del giocatore i ed è (debolmente) dominata se tra queste ne esiste almeno una che la domina (debolmente).

Definizione 3.3 - Equilibrio con strategie dominanti

Una combinazione di strategie tale che per ogni giocatore i la strategia è (debolmente) dominante costituisce un equilibrio in strategie (debolmente) dominanti.

La nozione di equilibrio in azioni dominanti è intuitiva e fornisce una previsione dell'esito di equilibrio del gioco molto attraente; infatti:

l'equilibrio è unico

i giocatori hanno un solo modo ragionevole di giocare.

Purtroppo, la gran parte dei giochi non ammette un equilibrio in azioni dominanti, vedi G.3.

G.3 - Battaglia dei Sessi

Se esiste tra le mosse del giocatore una strategia dominante, è naturale attendersi che essa verrà giocata, escludendo di norma la scelta delle strategie alternative. Allo stesso modo si può escludere che vengano giocate strategie dominate in quanto vi sono alternative che garantiscono guadagni maggiori.

Il fatto che esistano strategie dominanti è noto non solo al giocatore ma anche a tutti gli altri. Tutti perciò dovranno ovviamente tener conto, scegliendo le rispettive mosse,  del fatto che uno di loro giocherà con certezza la strategia dominante di cui dispone.

La soluzione di un gioco con dominanza iterata e induzione a ritroso si ha applicando la dominanza debole ed eliminando progressivamente non intere strategie, ma azioni o insieme di informazioni (nodi di decisione) che renderebbero qualsiasi strategia (almeno debolmente) dominata.

Definizione 3.4 - Dominanza iterata

Per ogni giocatore i, definiamo la successione di insiemi di strategie pure e per k=1,2.. Un gioco si dice risolubile per dominanza se esiste un numero t tale che contiene un unico elemento per ogni i. La combinazione di strategie si chiama soluzione per dominanza iterata. Se esiste, la soluzione per dominanza iterata è unica.

In un gioco in forma estesa con informazione perfetta dove ogni giocatore non è mai indifferente fra due nodi terminali, la procedura di dominanza iterata corrisponde al metodo di induzione a ritroso (backward induction). Quest'ultimo consiste nell'eliminare le mosse dominate partendo dai nodi terminali e risalendo l'albero a ritroso.

G.4 - Dominanza iterata

In G.4 la strategia b₁ domina la b₂. Il giocatore A (che non possiede strategie dominanti), può però ritenere ragionevole che B sceglierà b₁ e dunque opterà per scegliere a₁. Un meccanismo di questo genere, da parte del giocatore A prevede l'applicazione del criterio della dominanza iterata.

Critiche al criterio della dominanza

Il criterio della dominanza non prende in considerazione motivazioni di prudenza. Nel caso del gioco G.5 dove c'è un payoff di -100, è probabile che il giocatore A preferisca optare per la strategia a₂ che è più sicura in questo modo preferirà optare per un criterio che massimizza la sicurezza, senza tenere in considerazione i criteri di stretta razionalità sui quali si basa il criterio stesso di dominanza.

G.5

Un criterio basato sulla massimizzazione della sicurezza è il criterio di massiminimo in base al quale si considera qual è l'esito peggiore in corrispondenza di ogni possibile scelta e si effettua poi la scelta che conduce al migliore tra gli esiti peggiori. E' un criterio di scelta razionale in giochi a somma costante, ma non lo è in giochi a somma variabile nei quali non è detto che il meglio per un giocatore coincida con il peggio dell'altro.

Definizione 3.5 - Soluzione di Sicurezza

Dato un gioco C, chiamiamo valore di massiminimo in strategie pure per il giocatore i la quantità Ogni strategia pura che ottiene il valore di massiminimo si chiama strategia di massiminimo. Ogni combinazione di strategie prudenti costituisce una soluzione di sicurezza per il gioco G.

E' facile controllare che se G è un gioco a somma nulla, vale

Così che il massiminimo del giocatore 2 può essere scritto come l'opposto del minimassimo del giocatore 1.

Il criterio della dominanza non garantisce l'unicità delle strategie di equilibrio. Nel gioco G.6 che segue, B potrebbe ragionare:

dal momento che a₁ è debolmente dominata da a₂, A sceglierà a₂, pertanto B ha convenienza a giocare b₂, determinando un equilibrio in (a₂, b₂).

A potrebbe ragionare b₃ è dominata dalle altre 2 strategie di cui dispone B, quindi escluso b₃, per A è assolutamente indifferente giocare a₁ o a₂ : esito potrebbe quindi esser diverso da (a₂, b₂).

G.6

non vi è un univoco risultato del gioco.

Soluzioni ovvie

Nel gioco G.7 la coppia di strategie (a₁, b₁) si impone come equilibrio, eppure non è frutto di scelte che seguono il criterio della dominanza (a1 non è dominante su a₂ e b₁ non lo è su b₂). Tuttavia, se i giocatori avessero la possibilità di accordarsi preventivamente avrebbero entrambi l'interesse a stabilirsi su (a_1, b₁).

La (a₁, b₁) non è frutto di strategia di massiminimo: questa infatti condurrebbe a (a₂, b₂).

G.7

Equilibrio ovvio: è quel equilibrio in corrispondenza del quale nessun giocatore trae vantaggio dallo spostarsi, nel senso che non solo egli non ha incentivo a deviare dalla propria scelta ma neppure che gli altri giocatori devino dalle proprie scelte (equilibrio self enforcing).

Equilibrio di NASH

Una soluzione costituisce equilibrio di Nash (1951) quando le strategie di ciascun giocatore rappresentano la scelta migliore, date le migliori altrui strategie. In altri termini, un equilibrio è di Nash se ciascun giocatore, una volta osservate le scelte degli altri, non ha alcun interesse a cambiare la propria.

L'equilibrio di Nash gode della proprietà di stabilità (ciascuno ha interesse a confermare la propria scelta, una volta rilevata la mossa dell'avversario).

G.8

In G.8, (a₁, b₁) è un equilibrio di Nash ed è l'unico punto stabile. Se B avesse infatti conosciuto la scelta di A (a₁) avrebbe confermato la propria scelta b₁.  Se A avesse saputo che B avrebbe scelto b₁, avrebbe confermato a₁: questo è sufficiente per stabilire che (a₁, b₁) è un equilibrio di Nash.

(a₂, b₂) non è un equilibrio di Nash perché se A avesse conosciuto la mossa di B (b₂) non avrebbe scelto a₂, ma a₁. Analogo ragionamento si può fare per (a₁, b₂) e (a₂, b₁).

L'equilibrio di Nash si autoimpone (self enforcing) posto che l'avversario giochi la mossa dell'equilibrio di Nash, ciascuno è indotto a sua volta a giocare la propria mossa di eq. Nash. Se i giocatori sono razionali ed intelligenti: l'unica allocazione sostenibile è quella dell'eq. di Nash.

Si può mostrare che un equilibrio che sia frutto di strategie dominanti è anche un equilibrio di Nash (ma non vale il contrario).

DEFINIZIONE 3.5 - Equilibrio di Nash

Dato un gioco G, chiamiamo equilibrio di Nash in strategie pure ogni combinazione di strategie tale che per ogni giocatore i e in ogni strategia . Sostituendo ovunque la lettera alla lettera otteniamo la definizione di equilibrio di Nash.

Un equilibrio di Nash richiede che la strategia di ogni giocatore i sia ottimale rispetto a ciò che fanno gli altri, nel senso che il giocatore i massimizza la sua utilità attesa quando ogni avversario si attiene alla sua strategia di equilibrio.

G.9 - Dilemma del Prigioniero

Il Dilemma del Prigioniero, illustra il conflitto tra incentivi individuali e incentivi collettivi (vedi successiva sezione 4).

Molteplicità degli equilibri di Nash

Non sempre l'equilibrio Nash gode della proprietà dell'unicità. Nel gioco G.10 abbiamo - per esempio - 2 eq. Nash, (a₁ b₂) e (a₂, b₁).

G.10

Assenza dell'equilibrio di Nash

Quando i giocatori hanno a disposizione sole le strategie pure (giocano cioè delle strategie a loro disposizione e non una combinazione probabilistica di esse) può esser che l'eq. Nash non esista.

G.11

Non esiste equilibrio frutto di strategie dominanti e neppure equilibrio ovvio. In G.11, l'equilibrio (a₂, b₂) non è un equilibrio ovvio B non avrebbe alcun motivo per non deviare dalla scelta di b₂.

Esempio - Il gioco del contribuente

In questo gioco ci sono due giocatori: il contribuente e l'ispettore fiscale. Il contribuente deve decidere se evadere le tasse o fornire dichiarazione veritiera. L'ispettore deve decidere se controllare o meno la dichiarazione dei redditi considerando il costo che incorre nel controllare.

G.12

Si noti che non esiste equilibrio di Nash: questo è conseguenza del fatto che le preferenze sono cicliche. Se l'ispettore non controllasse per il contribuente sarebbe ottimale evadere. Se questi evade, però, per l'ispettore è ottimale controllare. Ma posto che l'ispettore controlli al contribuente conviene non evadere e se il contribuente paga le tasse il comportamento migliore per l'ispettore è non effettuare il controllo.

Unicità e non soluzione

Non esistenza e non unicità sono difetti dell'equilibrio di Nash. Inoltre, alcune soluzioni possono non essere convincenti anche se uniche.

G.13

Nel G.13 pur essendo (a_3, b₃) l'unico equilibrio di Nash, nessuno dei giocatori si augura di pervenirvi. E' evidente che entrambi i giocatori auspicano di collocarsi su una delle quattro caselle con payoff superiori a 20 pur non configurando tra esse nessun equilibrio di Nash.

Giochi in forma estesa a somma variabile: alcuni criteri di soluzione

La forma estesa evidenzia l'ordine in cui i giocatori muovono (ordine che può non essere per nulla temporale, ma bensì puramente logico), le informazioni e le strategie a disposizione dei giocatori, ed i payoff conclusivi. Risulta un forma ad albero.

I. Se il gioco è ad informazione perfetta la presentazione ad albero mette opportunamente in luce la successione temporale delle scelte fatte.

II. Se invece il gioco è ad informazione imperfetta il giocatore non è a conoscenza della sequenza delle mosse precedenti la sua decisione e il set informativo sarà caratterizzato da più nodi. Questo è un modo alternativo per dire che il gioco è di natura statica e simultanea.

III. Ricordiamo, inoltre, che se è possibile escludere qualsiasi incertezza di tipo esogeno, il gioco è ad informazione completa ovvero è caratterizzato da common knowledge.

IV. Identifichiamo come supergioco l'intero albero e definiremo sottogioco (proprio) ciascun sottoinsieme del supergioco avente origine da un nodo.

Backward induction. (induzione a ritroso) detto anche algoritmo di Kuhn (1953). Si procede a ritroso, partendo dai sottogiochi conclusivi, allo scopo di individuare l'equilibrio perfetto nei sottogiochi (subgame perfect equilibrium).

Al fine di produrre un equilibrio perfetto occorre che le strategie adottate dai giocatori producano un equilibrio di Nash in qualunque punto (leggi sottogioco) dell'albero, anche al di fuori del sentiero di equilibrio (cioè anche in un punto del gioco che potrebbe non essere mai effettivamente raggiunto).

In definitiva, si perviene allo stesso percorso di equilibrio, qualunque sia il punto di partenza del gioco. L'idea di fondo è quindi quella di individuare gli equilibri di Nash che non comportano la scelta di strategie non credibili da parte dei giocatori.

G.14 - Forma normale

Il gioco G.14 è caratterizzato dalla presenza di due equilibri di Nash:   (a₁, b₁) e (a₂, b₂). Per capire quale dei due verrà effettivamente giocato possiamo ricorre al criterio della dominanza iterata che permette di concludere che, essendo la strategia b₂ debolmente dominata dalla b₁, i giocatori si collocheranno sulla casella (5,2).

Un modo alternativo di ragionare e risolvere il gioco è quello di ricorre alla rappresentazione in forma estesa: ad un medesimo gioco possono corrispondere più rappresentazioni in forma estesa, ma una sola in forma strategica.

G.14 - Forma estesa

A

a a

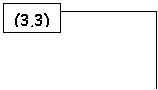
B

b b

	(5,2)

 

A

a₁ a₂

b b b b

(5,2) (1,1) (3,3) (3,3)

Ovviamente la rappresentazione 1) è la più significativa, in quanto sottolinea come la scelta del giocatore B sia irrilevante nel caso il giocatore A abbia scelto la strategia a₂. Ma andiamo per ordine.

Il giocatore A può evitare di scegliere la strategia a₁, scegliendo in tal modo la strategia a₂, perché in tal caso B minaccia di scegliere b₂. Tuttavia, se ci limitiamo al sottogioco che prende avvio dal nodo corrispondente alla mossa di B, ovvero supponiamo che A abbia scelto effettivamente a₁, a B conviene comunque giocare b₁, perché ottiene un payoff pari a 2. Vale a dire che la minaccia su cui si regge l'equilibrio (a_2, b₂) non è credibile. La coppia (a_1, b₁) individua quindi l'unico equilibrio perfetto del gioco (Si noti che il risultato coincide con quello fornito dal criterio della dominanza, ma questo è sempre vero).

Fallimento del criterio di Backward induction. Sebbene questo criterio dia dei risultati soddisfacenti, possono presentarsi casi in cui la sua applicazione conduce ad equilibri che sembrano andare contro ogni logica. L'esempio più noto è il gioco del Centipede di Rosenthal (1981).

L'albero del gioco si articola su di un numero arbitrariamente alto di nodi per ogni giocatore. In corrispondenza di ogni singolo nodo l'individuo può scegliere se chiudere (Mossa C) oppure passare (Mossa P) la mano all'altro.

G. 15

X Y X Y X Y X Y

P P P P P P P P

C C C C C C C

(1,1) (0,3) (2,2) (1,4) (3,3) (2,5) (4,4) (3,6)

La sequenza (virtuale) viene aperta dal giocatore X e chiusa dal giocatore Y. I nodi dispari (giocatore X) offrono ad entrambi lo stesso payoff, definito semplicemente dalla sequenza dei numeri naturali. I nodi pari (giocatore Y) forniscono coppie di payoff così definite: se indichiamo con i la sequenza dei nodi dispari, il generico nodo pari sarà j=i+1 e la coppia di payoff associata sarà (i-1, i+2).

Se applichiamo il criterio della backward induction partendo dall'ultimo nodo otteniamo che in corrispondenza dell'ultimo nodo il giocatore Y sceglierà C (perché 6>5): essendo conscio di questo il giocatore X sceglierà in corrispondenza del penultimo nodo C (perché 4>3). Consapevole di ciò, Y al terzultimo nodo opterà per C che garantisce 5>4. entrambi X e Y sceglieranno sempre C fino ad (1,1) che rappresenta un payoff subottimale rispetto ai payoff che si sarebbero potuti ottenere.

risultato insoddisfacente dal punto di vista teorico e poco credibile su quello reale: 2 giocatori dotati di razionalità operativa si spingeranno avanti nello sviluppo del gioco.

esperienza empirica mostra come non ci possa essere rigida applicazione dei criteri di soluzione individuati dall'elaborazione teorica (i.e.: criterio backward induction).

Le strategie miste

Un giocatore potrebbe scegliere di giocare non una delle strategie pure di cui dispone, in modo secco, ma giocare una combinazione probabilistica di due o più strategie. Ad esempio legare la scelta al fatto che nel lancio di una moneta esca testa o croce. Si parla in tal caso di strategia mista (vedi definizione nella precedente sezione 2) .

VANTAGGI:

I. Nel caso di strategie miste non ha più senso parlare di induzione certa rispetto alle strategie degli avversari (viene vanificato ogni tentativo di spionaggio).

II. Si dimostra che nell'ambito delle strategie miste l'equilibrio di Nash esiste sempre quando il numero di giocatori e di strategie è finito.

III. Con le strategie miste dovrà essere introdotto anche il concetto di payoff atteso (utilità attesa), inteso come la media ponderata dei payoff puri applicando come pesi di ponderazioni le probabilità assegnate da ciascuno giocatore alla scelta delle strategie pure. Utilità attesa: media ponderata delle utilità associate ai possibili esiti elementari.

Dominanza nelle strategie miste

Come abbiamo già visto in questo gioco entrambi i giocatori cercheranno di sfuggire all'unico equilibrio di Nash di strategie pure (1,1) per collocarsi su una delle quattro caselle di Nord-Ovest.

G.16

Possiamo immaginare allora che le intenzioni di A siano le seguenti: lancio una moneta bilanciata se esce testa gioco a₁ altrimenti gioco a₂. Supponiamo che lo stesso faccia B. Il payoff atteso di A risulta essere 23 e quello di B è 25 (Ovviamente ex-post A riceverà 24 o 22 e B 24 o 26).

Le grandezze attese sono comunque superiori in ogni caso alle utilità associate alle scelte a₃ e b₃. Siamo quindi in presenza di una strategia dominata. Cioè per entrambi i giocatori A e B, la strategia mista del tipo: gioco a₁ (b₁) con probabilità ½, a₂ (b₂)  con probabilità ½ e a₃ (b₃) con probabilità zero, domina la strategia a pura a₃ (b₃).

Inoltre, l'equilibrio derivante dal gioco della strategia mista è un equilibrio di Nash, in quanto nessun giocatore avrebbe potuto scegliere una strategia migliore, data le strategia scelta dall'avversario.

in G.16: 2 equilibri di Nash, uno in strategie pure (1,1); l'altro in strategie miste.

Equilibrio di Nash con strategie miste

Nell'esempio la distribuzione di probabilità scelta per la strategia mista è stata (½, ½ ,0). In verità, la scelta di questa distribuzione dovrebbe essere tale da rendere massimo il livello di payoff atteso (espresso in termini di utilità cardinali) di ciascun giocatore.

PROBLEMA: Scelta di distribuzione della probabilità. Come avviene tale scelta? La scelta della distribuzione delle probabilità deve esser tale da rendere max il livello di utilità attesa di ogni giocatore.

G.17

In G.17 non esiste alcun equilibrio di Nash nell'ambito delle strategie pure. Per definizione, essendo finito il numero di giocatori ed il numero delle strategie pure, sicuramente esisterà un equilibrio di Nash tra le strategie miste. Possiamo immaginare che il problema di A sia quello di attribuire una opportuna probabilità alla scelta a₁ ed alla scelta a₂ .

Siano rispettivamente p₁ e p₂ le probabilità, con p₁+p₂=1. Simmetricamente siano v₁ e v₂ le rispettive probabilità applicate da B rispettivamente alla scelta b₁ e b₂. Naturalmente vale v₁+ v₂=1.

Combinando le due strategie miste, la probabilità che l'esito finale risulti (a₁,b₁) è pari a p₁v₁ e così per gli altri 3 risultati; scriviamo l'utilità attesa dal giocatore A:

E(U)A=2p₁v₁+3p₂v₁+2 p₁v₂+1p₂v₂

Ossia, dopo calcoli banali e sostituzioni:

E(U)A= p₁(1-2v₁)+2v₁+1

Nello stesso modo si trova l'utilità attesa del giocatore B

E(U)B= v₁(4p₁-3)-4p₁+5

In questo modo si può osservare che le uniche scelte che assicurano l'equilibrio del gioco (con massima utilità attesa per ciascuno) sono:

da parte di A:    p₁=3/4 p₂=1/4; E(U)A=2

da parte di B: v₁=1/2 v₂=1/2; E(U)B=2

L'esito derivante rappresenta un equilibrio di Nash: infatti, ogni diversa attribuzione di probabilità da parte di A o di B avrebbe spinto l'altro individuo ad una scelta pura, per aumentare la propria utilità; si sarebbe così ritornati nel dominio delle strategie pure, dove già sappiamo non esservi stabilità. Si è così mostrato un gioco privo di equilibrio nelle strategie pure, ma con equilibrio di Nash tra le strategie miste.

Alcuni giochi importanti

Il dilemma del Prigioniero

La configurazione del gioco è la seguente: la polizia custodisce in celle diverse due individui accusati di essere complici di uno stesso crimine. Tuttavia, non disponendo di prove sufficienti a comminare ai due una pena più che simbolica, gli inquirenti cercano di indurre i detenuti a confessare, promettendo clemenza.

Nella tabella compaiono gli anni di reclusioni inflitti a seconda del comportamento dei due prigionieri, i quali debbono decidere se confessare  (C) oppure non confessare (NC).

G.18

L'equilibrio di Nash (che è anche equilibrio nelle strategie dominanti) è individuato dalla combinazione (C,C) che comporta per entrambi 5 anni di reclusione.

Si noti che l'adozione di un criterio di razionalità individuale conduce ad un risultato subottimale nel senso di Pareto, perché è peggiore di quello che potrebbero ottenere se nessuno dei 2 confessasse. Non basta, questo è anche il risultato complessivamente peggiore, dal momento che comporta un totale di 10 anni di carcere. Se i due prigionieri potessero comunicare e stipulare un accordo vincolante, potrebbero adottare entrambi la strategia dominata (NC, NC) ed ottenere il risultato ottimale (-1,-1). Questo non avviene perché quando ci sono pochi agenti (oligopolio) in generale si creano delle esternalità.

Il gioco del pollo (chicken game)

La configurazione del gioco è la seguente: immaginiamo due ragazzi che percorrono una stretta strada in senso opposto e quando si avvistano, debbono decidere se deviare oppure no. Se entrambi deviano il gioco finisce in parità (-1,-1). Se entrambi tirano diritto, succede il disastro (-5,-5). Se uno devia e l'altro no, quello che ha deviato subisce una penale e l'altro riceve un premio. (Esempio reale due paesi in guerra che devono decidere se sferrare un attacco militare).

G.18

Vi è una perfetta simmetria tra i guadagni spettanti ai due giocatori, ma a differenza del dilemma del prigioniero, nel gioco del pollo non esistono strategie dominanti ed esistono due equilibri di Nash. Non è chiaro quale di questi due rappresenta la situazione che verrà affettivamente a determinarsi.

Ciascuno dovrebbe convincere l'altro a giocare la strategia arrendevole assicurando che egli si impegna fermamente (inflessibilmente) a giocare la strategia NO.

Se i due giocatori sono identici, non si può sapere a priori quale sarà l'esito del gioco. Se i due giocatori sono invece diversi potrebbero esserci considerazioni di reputazione e di inflessibilità ad indicare quale sarà la conclusione del gioco. In altre parole, la soluzione del gioco del pollo è ovvia soltanto se esiste una differenza di forza, o di determinazione, o di reputazione tra i due giocatori, che sia nota ad entrambi e che spinga l'uno ad essere arrendevole e l'altro ad essere inflessibile.

La battaglia dei sessi

La configurazione del gioco è la seguente:  C'è una Valentina (giocatore A) e un Valentino (giocatore B) che devono decidere cosa fare la sera di San Valentino. Tuttavia, i due non possono (o non riescono) a comunicare. Entrambi sanno però che Valentino desidera ardentemente andare al cinema e Valentina andare a vedere un incontro di pugilato. Inoltre, entrambi odiano stare soli la sera di San Valentino e pur di stare assieme all'amato/a accettano di buon grado di andare allo spettacolo preferito dall'altro/a. I due amanti devono, senza sapere cosa farà l'altro, decidere dove andare.

G.19

In questo gioco ci sono due equilibri di Nash in strategie pure: (Cinema, Cinema) e (Pugilato, Pugilato). Si nota anche che questi due equilibri non sono strategie dominanti per nessuno dei due giocatori. Infatti Valentina, preferisce andare al Cinema solo se Valentino va la Cinema, altrimenti preferisce andare al Pugilato.

Questo gioco mostra un classico problema di coordinamento. Se i due giocatori si coordinano finiscono per stare meglio entrambi, tuttavia non vi sono meccanismi ovvi di coordinamento, poiché i due giocatori hanno ordinamenti opposti circa i due equilibri. (Esempio reale: tutti i processi di contrattazione possono essere visti come problemi di coordinamento).

6. Pluralità di Equilibri

Caratteristiche dell'eq. di Nash e necessità di introdurre i refinements:

l'equilibrio di Nash non sempre esiste in strategie pure

non sempre è unico

anche quando è unico, non è detto che sia la soluzione desiderabile del gioco

le strategie miste garantiscono che un equilibrio di Nash esista sempre, ma questo solo se il numero di giocatori e il numero di strategie è finito.

Quando vi sono più equilibri di Nash, quale può esser considerata la soluzione del gioco?

Sono stati proposti alcuni criteri (refinements) che si prefiggono di perfezionare uno tra i molteplici equilibri che potrebbero emergere dal gioco, in modo da giudicarlo per qualche motivo "migliore" degli altri.

In altre parole, la teoria dei giochi mette in evidenza come, in certe circostanze, siano possibili diverse configurazioni di equilibrio. Per stabilire quale effettivamente si verrà a determinare, non è sufficiente limitarsi a studiare tali equilibri, ma occorrono considerazioni ulteriori, che possono esser relative sia alla struttura complessiva dei payoffs, sia a fattori esogeni.

Ordinamento Paretiano degli equilibri di Nash

E' rara la circostanza che tra gli equilibri di Nash ve ne sia uno Pareto-dominante, cioè che presenti dei payoffs per ciascun giocatore NON  INFERIORI ai payoffs garantiti dagli equilibri e, per almeno un giocatore, strettamente maggiore.

Se esiste tra gli equilibri di Nash uno che è Pareto-dominante, possiamo pensare che esso dia la soluzione del gioco: non è consueto!

In un gioco che presenti più equilibri di Nash, potremo pensare di ordinare tali equilibri in base a criteri "Collettivi".

G.20

Se tra gli equilibri di Nash ne esiste uno Pareto-dominante, possiamo pensare che esso sia la soluzione del gioco. Ma può verificarsi il caso di un equilibrio di Nash che è pure Pareto-dominante rispetto ad altri equilibri, ma non rappresenti la soluzione del gioco.

G.20 presenta 2 equilibri di Nash (4,3) e (8,9). Il secondo è Pareto-dominante rispetto al primo (8>4) e (9>3) si sarebbe tentati di dire che (a₂, b₁) è la soluzione del gioco. Ma non è così: a₂ è dominata da a₁ (anche se in senso debole).

Il criterio Paretiano, tuttavia, è minato da una lacuna assai più grave della rarità che ne caratterizza l'applicabilità. Infatti, può verificarsi il caso che un equilibrio di Nash, che è pure Pareto dominante sugli altri equilibri, non rappresenti la soluzione del gioco per motivi di sicurezza.

Nel gioco G.20, l'equilibrio (a₁, b₂) è dominante e quindi più sicuro dell'equilibrio (a₂, b₁).

Refinement: eliminazione di equilibri con strategie dominate.

Affinchè un equilibrio di Nash possa essere un equilibrio del gioco: deve escludere tutti gli equilibri che coinvolgono strategie dominate (a₁, b₂) in G.20 coinvolge una strategia dominata.

Subgame perfection

Abbiamo già introdotto il concetto di equilibrio perfetto nei sottogiochi alla Selten. Ora, lo stesso concetto verrà esaminato come refinement dell'equilibrio di Nash.

Si osservi il gioco G.22. Il giocatore B è un produttore già presente nel mercato come monopolista, ed A è un'impresa potenziale entrante nel mercato. Il giocatore A dispone di due strategie: Entrare (a₁), Non entrare (a₂). Il giocatore B dispone di due strategie: Combattere (b₁), Colludere (b₂). Vi sono due equilibri di Nash: (a₁, b₂) (entrare, collusione) e (a₂, b₁) (non-entrare, guerra).

G.22 (forma normale)

In questo gioco le mosse dei giocatori non avvengono simultaneamente: prima A decide se entrare oppure no; in un secondo momento B decide, se A è entrato, di combattere oppure no.

La raffigurazione più adeguata è quella estesa.

G.22 (forma estesa)

guerra (-1, -1)

B

entra collude

A 

Non entra (0, 40)

Se il gioco iniziasse nel nodo B, il risultato di equilibrio sarebbe (Entra-Collude). Tale equilibrio gode dunque della subgame perfection alla Selten.

Il risultato (Non entra - Guerra), invece, non è raggiungibile se si parte da un punto del gioco che sia differente dal nodo A e pertanto non può esser giudicato perfetto.

Ciò non vuol dire che (a₂, b₁) non sia un equilibrio di Nash. Ma non ha un senso economico: non ha senso per il giocatore B combattere se l'impresa A decide di non entrare nel mercato!

Convenzioni sociali

Se esistono più equilibri e non esiste alcun "modo ovvio" di giocare e nessuno degli equilibri di Nash, bisogna ricorrere ad altri criteri. Bisogna introdurre degli elementi aggiuntivi che permettano di superare l'impasse dell'incertezza nella definizione dell'equilibrio.

In particolare:

esistenza convenzioni sociali che permettano di selezionare un equilibrio

si può pensare che il gioco venga ripetuto più volte e che intervengano fenomeni di learning (apprendimento).

Si consideri il gioco della "precedenza" G23. Il luogo in cui si svolge è un crocevia, i giocatori sono gli automobilisti 1 (che viene da sinistra) e 2 (che viene da destra), che dispongono della medesima coppia di strategie: F=fermarsi e P=passare.

G.23

Il gioco presenta due equilibri di Nash: (1F, 2P) e (1P, 2F) la teoria dei giochi può servire a spiegare la nascita delle istituzioni sociali: quando a priori non è evidente quale gioco verrà giocato, può intervenire la convenzione sociale (es. precedenza da dx). La convenzione sociale secondo la quale ha precedenza chi viene da destra porta (1F, 2P), l'equilibrio che viene effettivamente giocato.

Ma allora le convenzioni possono nascere come equilibrio di un gioco, magari ripetuto?

Learning

Consideriamo il gioco della "Battaglia dei Sessi", tipo G.19.

Le strategie possibili sono C=andare al cinema, e P andare all'incontro di pugilato. Assumiamo che lui preferisca P e lei preferisca C. Tuttavia entrambi traggono maggior profitto dalla compagnia dell'altro/a.

Abbiamo due equilibri (C,C) e (P, P)

G.19

Una società fortemente maschilista potrebbe indurre a ritenere che l'equilibrio sarà (P, P). Si tratta in questo caso di una convenzione esogena che impone un equilibrio piuttosto che un altro (si ricade nel caso precedente).

Possiamo, tuttavia, pensare ad un equilibrio endogeno. Se il gioco fosse ripetuto i giocatori potrebbero stabilire (piu' o meno implicitamente), un accordo che preveda l'alternanza un round dopo l'altro, dei due equilibri.

Focal Point

Tirole (1988) identifica il genere di equilibrio del gioco precedente - frutto del meccanismo dell'alternanza - come focal equilibrium.

Più in generale un focal point è un esito che si impone all'attenzione dei giocatori per la natura peculiare di esso all'interno della matrice dei payoff e che spinge i giocatori a sceglierlo. Vedi nel G.24 la coppia di strategie (a₅, b₅).

G.24

Giocare le strategie incrociate che danno (9,9) in assenza di comunicazione tra i giocatori, è un caso molto fortunoso. Esiste però una coppia di risultati soddisfacenti che è (8,8) ed essendo unica si segnala come focal point. E' vero che tale risultato è peggiore di (9,9) ma, essendo unico e non potendo i giocatori comunicare tra loro, potrebbe indurre i giocatori a far convergere verso la sua scelta: infatti, il giocatore A potrebbe pensare che il giocatore B ragioni in modo simile e quindi giocare (8,8).