AFFINITA' IN UN PIANO

La matrice A= si chiama matrice dell'affinità. Le (0) si chiamano equazioni dell'affinità.

Per quanto detto un'affinità T è una corrispondenza invertibile. Si può dimostrare che la corrispondenza inversa, quella che alla coppia (X,Y) associa la coppia (x,y), che indichiamo con T è anch'essa un'affinità.

Per le affinità valgono le seguenti proprietà (teoremi):

In un'affinità ad una retta corrisponde una retta (o equivalentemente, a tre punti allineati corrispondono tre punti ancora allineati).

In un'affinità a rette parallele corrispondono rette parallele.

In un'affinità a rette incidenti corrispondono rette incidenti.

In un'affinità è costante il rapporto delle aree 424f53e corrispondenti.

Tale rapporto si chiama rapporto d'affinità e si può dimostrare che esso è uguale al valore assoluto del determinante della matrice A dell'affinità.

Si danno inoltre le seguenti definizioni:

Definizione: Un'affinità di equazioni (1) e matrice A è detta

positiva, o diretta, se det(A)>0;       negativa, o inversa, se det(A)<0.

Definizione: Un punto (x,y) si dice unito in un'affinità se è il corrispondente (o immagine o trasformato) di se stesso, cioè se risulta

X=x,  Y=y.

Se un'affinità possiede un solo  punto unito tale punto è detto centro dell'affinità.

Definizione: Una retta si dice unita (o invariante o fissa) in un'affinità se è la corrispondente di se stessa. Inoltre, se è luogo di punti uniti si dice puntualmente unita ( o puntualmente invariante o puntualmente fissa); altrimenti si dice globalmente unita (o globalmente invariante o globalmente fissa).

Definizione: Una proprietà di una figura F si dice invariante per una trasformazione se essa risulta verificata anche dalla figura F (o, come suol dirsi, si conserva nella figura F ) corrispondente di F tramite la trasformazione.

Qui di seguito elenchiamo le proprietà invarianti per un'affinità:

l'allineamento di tre punti (pertanto un'affinità trasforma rette in rette);

il parallelismo (pertanto un'affinità trasforma rette parallele in rette parallele, senza peraltro conservare la direzione);

l'incidenza (pertanto un'affinità trasforma rette incidenti in rette incidenti, senza peraltro conservare l'ampiezza degli angoli);

il punto medio (pertanto il punto medio M di un assegnato segmento AB avrà come immagine, tramite l'affinità, un punto M che risulterà essere punto medio del segmento A B immagine, tramite l'affinità del segmento AB).

Riportiamo alcuni esempi di proprietà che non sono invarianti:

distanza fra due punti (o equivalentemente, lunghezza di un segmento);

la direzione;

l'ampiezza degli angoli.

Possiamo pertanto affermare che un'affinità non conserva né le dimensioni (poiché non conserva la lunghezza) né la forma (poiché non conserva gli angoli).

Inoltre mentre è vero che in un'affinità è costante il rapporto delle aree 424f53e di figure corrispondenti, non risulta, in generale, costante il rapporto di segmenti corrispondenti. Tuttavia, se due segmenti sono paralleli e hanno un certo rapporto, allora anche i loro segmenti corrispondenti hanno lo stesso rapporto; così se AB è parallelo a CD ed il loro rapporto vale k, anche il rapporto fra i segmenti corrispondenti A B e C D dovrà valere k.

Infine diamo la seguente definizione:

Definizione: Si chiamano proprietà affini quelle proprietà delle figure che si conservano nelle loro immagini ottenute mediante un'affinità.

Anticipiamo che esistono particolari affinità per le quali è costante il rapporto di due qualsiasi segmenti corrispondenti; tali affinità prendono il nome di similitudini. In virtù di quanto affermato si può dire che l'insieme delle similitudini è un sottoinsieme (proprio) di quello delle affinità.

Vogliamo provare con un esempio che un'affinità conserva il rapporto fra due segmenti paralleli (ovvero il rapporto fra segmenti paralleli è un' invariante per un'affinità). A tal fine consideriamo l'affinità di equazioni:

e due segmenti paralleli  AB e CD di estremi A(0,0), B(1,2), C(-1,1), D(2,7). Si verifica facilmente che A'(1,-1), B'(0,3), C'(-1,-2), D'(-4,10) e che ==.

Inoltre vogliamo segnalare un'altra proprietà delle affinità:

un'affinità diretta conserva il verso di percorrenza delle figure;

un'affinità inversa non conserva il verso di percorrenza delle figure.

Per convincersene basta disegnare tre punti A, B, C e i loro corrispondenti A', B',C' nell'affinità in esame e verificare che il verso di percorrenza ABC è lo stesso di quello A'B'C' se l'affinità considerata è diretta, mentre è l'opposto nel caso in cui tale affinità è un'affinità inversa.

SIMILITUDINI NEL PIANO

Definizione: Si chiama similitudine piana un'affinità che trasforma una circonferenza in una circonferenza.

Si può dimostrare la seguente proprietà che caratterizza le similitudini piane:

Teorema: Un'affinità è una similitudine se e soltanto se è costante il rapporto di segmenti corrispondenti (rapporto di similitudine).

E' inoltre importante il seguente teorema:

Teorema: In un sistema cartesiano ortogonale, le equazioni di una similitudine sono del tipo:

(1)  oppure del tipo   (2) 

dove k, , p, q sono costanti reali e k>0.

Commento-dimostrazione: a tale risultato si giunge a partire dalle equazioni di un'affinità

imponendo che l'immagine della circonferenza di equazioni X+Y=1 sia ancora una circonferenza; ciò si verifica se e soltanto se valgono le seguenti relazioni:

(*)  

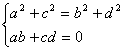
che rappresentano le condizioni analitiche cui debbono soddisfare i coefficienti di un'affinità per essere una similitudine.

Posto k =  , si può scrivere a = kcos e c = ksen; sostituendo le espressioni di a e c appena trovate nel sistema (*) si ottiene il sistema equivalente:

(**)  

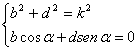
Risolvendo tale sistema rispetto a b e d si ottengono le soluzioni:

   e  

Sostituendo nelle (3) ad a, b, c, d i valori ora trovati si ottengono le (1) e le (2).

Il numero reale positivo k =  =   che compare nelle equazioni (1) e (2) di una similitudine prende il nome di rapporto di similitudine.

Esso rappresenta il rapporto costante tra segmenti corrispondenti in una similitudine (tale proprietà può essere facilmente dimostrata).

Poiché risulta a = kcos e c = ksen , le equazioni della similitudine assumono la forma:

)      oppure     (2 )  

essendo k =  il rapporto di similitudine.

Nelle (1 ) risulta  det(A) = a>0, mentre nelle (2 ) risulta  det(A) = a<0. Pertanto le (1 ) rappresentano le equazioni di una similitudine diretta di rapporto k = , mentre le (2 ) rappresentano le equazioni di una similitudine inversa di rapporto k = .

Qui di seguito elenchiamo le proprietà invarianti per una similitudine:

tutte le proprietà invarianti per un'affinità;

ampiezza degli angoli.

Inoltre una similitudine conserva il rapporto tra segmenti corrispondenti. Tale rapporto costante k, come già detto, prende il nome di rapporto di similitudine. Da questa proprietà discende in modo ovvio che in una similitudine è costante il rapporto dei perimetri di due figure corrispondenti (dette figure simili) e tale rapporto è pari al rapporto di similitudine k.

Elenchiamo alcune proprietà che non sono invarianti per una similitudine:

distanza fra due punti (o equivalentemente, lunghezza di un segmento);

direzione.

Per quanto detto si può affermare che le similitudini non conservano le dimensioni (poiché non conservano la distanza) ma conservano la forma (poiché conservano l'ampiezza degli angoli).

OMOTETIE

Se nelle equazioni (1) di una similitudine poniamo α=0 otteniamo:

(3)   ;

tali equazioni rappresentato le equazioni di una omotetia a patto che la trasformazione da esse rappresentata abbia uno ed un solo punto unito; ciò accade, come facilmente si verifica sse , risulta k 1 (e anche k>0 trattandosi di una similitudine); infatti:

    dunque la trasformazione considerata ammette uno ed un solo punto unito sse  1-k 0,  ovvero sse  k

Se invece risulta k=1 allora le equazioni (3), come facilmente si comprende, rappresentano una traslazione (trasformazione priva di punti uniti) di vettore v(p,q) se almeno uno fra i valori di p e q è diverso da zero (se p vel q 0), l'identità (o trasformazione identica) avente come punti uniti tutti i punti del piano se p=q=0. L'identità, trasformazione avente tutti i punti del piano uniti, può essere vista come una particolare omotetia, quella di rapporto 1; pertanto, a rigore, avremmo dovuto dire che le equazioni (3) costituiscono le equazioni di un'omotetia a patto che la trasformazione da esse rappresentata abbia almeno un punto unito.

Riepilogando possiamo dire che le equazioni

(3)  

con k>0 e k 1 rappresentano un'omotetia di centro C (il centro di un'omotetia è il suo unico punto unito) e rapporto k. Tale omotetia essendo stata ricavata da una similitudine diretta è una omotetia diretta. Il numero k, detto rapporto di omotetia rappresenta il rapporto costante fra segmenti corrispondenti.

Se, invece, nelle (3) si pone k=1 allora tali equazioni rappresentano quelle di una particolare omotetia (priva di centro poiché dotata di infiniti punti uniti), l'identità, solo se p=q=0, in caso contrario rappresentano le equazioni di una trasformazione priva di punti uniti, la traslazione di vettore non nullo v(p,q) la quale, essendo priva di punti uniti non è un'omotetia.

Se invece nelle equazioni (1) di una similitudine poniamo α=π otteniamo:

(4)   ;

posto h= k le (4) diventano:

(5) 

con h<0 (essendo k>0 poiché rapporto di similitudine).

Tali equazioni rappresentano le equazioni di una omotetia a patto che la trasformazione da esse rappresentata abbia uno ed un solo punto unito (o, almeno un punto unito, se vogliamo includere l'identià); ciò accade, come facilmente si verifica, per ogni valore negativo di h (cioè sempre); infatti:

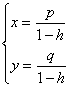    dunque la trasformazione considerata ammette uno ed un solo punto unito poichè  1 h 0,  ovvero h 1, essendo nelle (5) h<0.

Anche in questo caso l'omotetia, essendo stata ricavata da una similitudine diretta, è una omotetia diretta di rapporto k= h. Tale rapporto, come al solito, rappresenta il rapporto costante fra due segmenti corrispondenti.

Mentre le (3) definiscono un'omotetia che ad un punto P diverso dal suo centro C fa corrispondere un punto P' che si trova dalla stessa parte di P rispetto a C, le (5) definiscono un'omotetia che ad un punto P diverso dal suo centro C fa corrispondere un punto P' che si trova dalla parte opposta di P rispetto a C. Ecco perché talune volte si usa dire, impropriamente, che le omotetie di equazioni (3) sono omotetie dirette, mentre quelle di equazioni (5) sono omotetie inverse.

Ribadiamo invece che le omotetie sono sempre dirette (essendo particolari similitudini dirette), pertanto conservano il verso di percorrenza delle figure.

Le omotetie con k>1 e quelle con h< 1 sono degli "ingrandimenti", quelle con 0<k<1 e quelle con 1<h<0 sono delle "riduzioni".

Osserviamo infine che se nelle (5) poniamo h= 1 otteniamo:

(6) 

che sono le equazioni di una simmetria centrale il cui unico punto unito è il centro C.Alla luce di quanto detto possiamo affermare che le simmetrie centrali sono delle particolari omotetie di rapporto k=1 (rapporto costante fra segmenti corrispondenti) e che come tutte le omotetie sono delle trasformazioni dirette (conservano cioè il verso di percorrenza delle figure).

Qui di seguito elenchiamo le proprietà invarianti per una omotetia:

tutte le proprietà invarianti per una similitudine;

la direzione.

La proprietà (2) si dimostra immediatamente:

Sia r la retta di equazione y=mx+c e siano

le equazioni di un'omotetia (diversa dall'identità) di centro C. Ricaviamo le equazioni dell'omotetia inversa esprimendo x e y in funzione di X e Y:

;

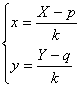l'equazione della retta r diventa:

  ovvero: Y=mX -mp+kc; tale equazione altro non è che l'equazione della retta r' immagine di r; come si vede chiaramente i coefficienti angolari delle due rette r ed r' sono uguali pertanto le due rette sono parallele. Resta così provato che l'omotetia conserva la direzione.

Non è invariante per omotetia la distanza fra due punti (lunghezza di un segmento).

Una notevole proprietà delle omotetie è la seguente: i punti corrispondenti sono allineati con il centro dell'omotetia.

Siano  le equazioni di un'omotetia di centro C (con k 1 ovviamente); le equazioni dell'omotetia possono essere scritte nella forma

essendo  e .

Dim.:

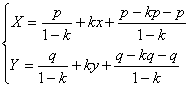;   ;      e posto

   si ha:   con C(x, y) centro dell'omotetia .

Osservazioni: Si può provare che la composizione di due omotetie aventi lo stesso centro C e rapporti k e k è ancora una omotetia di centro C e rapporto k=k.

La composizione di una omotetia con una traslazione dà per risultato ancora una omotetia avente lo stesso rapporto, ma centro diverso da quello dell'omotetia data.

La composizione di una omotetia con una simmetria assiale non è più una omotetia ma dà per risultato un nuovo tipo di  trasformazione detta similitudine. Più precisamente si dà la seguente

Definizione: Si chiama similitudine una corrispondenza biunivoca del piano in sé che sia il risultato  della composizione di una omotetia con una isometria.

Ossia: 

Similitudine = (omotetia) ◦ (isometria).

Tale definizione di similitudine è equivalente a quella da noi data precedentemente (lo si può provare).

ISOMETRIE NEL PIANO

Definizione: Si chiama isomeria (o congruenza o movimento rigido) piana ogni similitudine di rapporto 1.

Ponendo nelle equazioni (1) e (2) delle similitudini k=1 si hanno le isometrie, rispettivamente, dirette e inverse.

Per k=1 le (1) diventano:

(7) 

che sono le equazioni delle isometrie dirette o rototraslazioni.

Per α=0 e p e q non entrambi nulli si ha la traslazione di vettore v(p,q) di equazioni:

(8)  .

Per p=q=0 si ha la rotazione di centro l'origine delle coordinate e ampiezza α di equazioni:

(9)  .

Si comprende così il nome di rototraslazioni dato alle trasformazioni di equazioni (7): esse risultano dalla composizione, nell'ordine, di una rotazione di centro l'origine degli assi e ampiezza α con una traslazione di vettore v(p,q) o, come suol dirsi, dal prodotto di una traslazione e di una rotazione; in simboli:  rotot.=  t_v(p,q)◦R_O,α

Per α=π , dalle (7) si hanno le equazioni della simmetria centrale di centro C:      

(10)  .

Per k=1 le (2) diventano:

(11) 

che sono le equazioni delle isometrie inverse.

Le isometrie inverse possono essere:

simmetrie assiali;

glissosimmetrie (composizioni di una simmetria assiale con una traslazione).

Le (11) per p=q=0 diventano:

(12)

o, con notazione diversa:

                   (13) ,  con  a²+c²=1;

sia le (12) che le (13) rappresentano le equazioni di una simmetria assiale di asse la retta passante per l'origine e formante col semiasse positivo delle ascisse un angolo di ampiezza .

Dimostriamolo:

Consideriamo le (12) e troviamo gli eventuali punti uniti. Ponendo X=x e Y=y si ottiene il seguente sistema lineare omogeneo:

(14) ;

poiché risulta

= - cos²α + 1 - sen²α = 0

il sistema ammette soluzioni.

L'isometria possiede allora infiniti punti uniti e precisamente tutti quelli della retta avente per equazione una delle (14).

L'isometria è allora una simmetria avente per asse proprio la retta in questione. Come equazione dell'asse a scegliamo, per fissare le idee, la seconda delle (14) e cioè l'equazione:

x sen - (cos + 1)y = 0.

Tale asse passa per l'origine ed ha coefficiente angolare

m ===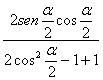 tg

Pertanto risulta m= tg e quindi, come volevamo dimostrare, la retta a forma con il semiasse positivo delle x l'angolo.

E' bene tener presente, se si usano le (13), che α = tg^-1.

Se nelle (11) p e q non sono entrambi nulli, si hanno, come già detto, le glissosimmetrie che sono le composizioni, nell'ordine, di una simmetria assiale di asse la retta passante per l'origine e formante col semiasse positivo delle ascisse un angolo di ampiezza  con una traslazione di vettore v(p,q) o, come suol dirsi, il prodotto di una traslazione per una simmetria assiale; in simboli: 

 glissosimm.= t_v(p,q)◦ s_o,α/2.

In particolare, per p=q=α=0 le (11) ci danno:

(12) 

che sono le equazioni della simmetria assiale di asse x

e per p=q=0 e α=π ci danno invece:

(13) 

che sono le equazioni della simmetria assiale di asse y.

Osservazione: Per quanto detto risulta chiaro che le equazioni:

(14) 

individuano un'isometria sse

(15)  .

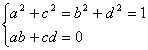e che :

se =1, l'isometria è diretta;

se invece = 1, l'isometria è inversa.

Evidentemente le (7) e le (11) possono scriversi nelle forme:

                      (16)       con  a²+c²=1

e

                      (17)    con  a²+c²=1.

Pertanto tutte le affinità aventi equazioni del tipo (16) e (17) con a²+c²=1 costituiscono delle isometrie, rispettivamente dirette e inverse (in esse a rappresenta cosα e c rappresenta senα).

Quadro riassuntivo sulle isometrie

Sono similitudini di rapporto

◦ Se det(A)=1: isometrie dirette;    ◦ se det(A)= −1: isometrie inverse.

a) Isometrie dirette

traslazioni:    ◦ nessun punto invariante;

◦ infinite rette globalmente invarianti: quelle parallele al segmento       orientato che individua la traslazione.

simmetrie centrali:    ◦ un punto invariante: il centro;

               ◦ infinite rette invarianti: quelle passanti per il centro.

rotazioni:    ◦ un punto invariante: il centro;

  ◦ nessuna retta invariante.

rototraslazioni

b) Isometrie inverse

simmetrie assiali:    ◦ una retta puntualmente invariante: l'asse;

  ◦ infinite rette globalmente invarianti: le perpendicolari all'asse.

glissosimmetrie:    (composizioni di una simmetria assiale con una traslazione)

 ◦ una retta globalmente invariante: l'asse della simmetria.

Relativamente alla composizione di isometrie non è difficile provare quanto sgue:

la composizione di due traslazioni dà per risultato ancora una traslazione di vettore pari alla somma dei vettori che individuano le traslazioni componenti;

in generale, componendo due simmetrie (ortogonali) assiali s e s, il risultato non è una simmetria assiale;

la composizione di due simmetrie (ortogonali) assiali s e s, di assi a e b paralleli è una traslazione;

la composizione di due simmetrie (ortogonali) assiali s e s, di assi a e b perpendicolari è una simmetria centrale di centro il punto P di intersezione degli assi a e b;

la composizione di due simmetrie (ortogonali) assiali s e s di assi a e b che non siano né paralleli né perpendicolari è una rotazione di centro il punto P di intersezione degli assi a e b e ampiezza pari al doppio dell'ampiezza dell'angolo acuto formato dalle due rette a e b;

la composizione di due simmetrie centrali di centri distinti è una traslazione;

la composizione di due rotazioni aventi lo stesso centro è ancora una rotazione di centro pari al centro delle rotazioni componenti e ampiezza pari alla somma delle ampiezze delle rotazioni componenti.

Infine, poiché tanto le rotazioni quanto le traslazioni possono ottenersi come prodotto di due simmetrie assiali, tenuto conto di quanto osservato a proposito delle isometrie dirette e inverse, possiamo affermare quanto segue:

un'isometria diretta è il prodotto di un numero pari di simmetrie assiali;

un'isometria inversa è il prodotto di un numero dispari di simmetrie assiali.

LE SIMMETRIE ORTOGONALI ASSIALI

Si chiama simmetria ortogonale assiale di asse r una corrispondenza biunivoca del piano in sé  che ad ogni punto P associa il puntoche si ottiene con le seguenti condizioni:

1)

2) oppure  , con M punto medio del segmento PP' e M(x_M,y_M)

Per trovare l'equazione di una simmetria di  asse (di simmetria) r bisogna trasformare le due condizione algebricamente.

Per trovare le coordinate dell'immagine di un puntobisogna sostituire le coordinate del punto iniziale (P) alla x e alla y nell'equazione della simmetria.

Per trovare l'equazione dell'immagine di una rettabisogna sostituire i valori di x e di y dell'equazione della simmetria inversa nell'equazione della retta iniziale.

Simmetria con asse di simmetria parallelo all'asse X

 

quindi

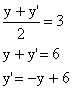    Trovo

 Equazione della simmetria

 Equazione della simmetria inversa

Esempio 1 (simmetria di un punto):

 

Cordinate di

Esempio 2 (simmetria di una retta):

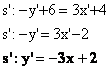
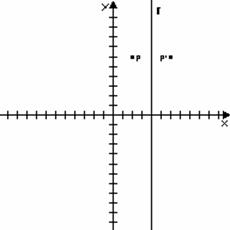
Simmetria con asse di simmetria parallelo all'asse Y

quindi

    Trovo

 Equazione della simmetria

 Equazione della simmetria inversa

Esempio 1 (simmetria di un punto):

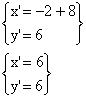
Cordinate di

Esempio 2 (simmetria di una retta):

Simmetria avente l'asse X come asse di simmetria

Questa simmetria ha una sua equazione della simmetria che e:

 Equazione della simmetria inversa

Esempio 1 (simmetria di un punto):

 

Cordinate di

Esempio 2 (simmetria di una retta):

Simmetria avente l'asse Y come asse di simmetria

Questa simmetria ha una sua equazione della simmetria che e:

 Equazione della simmetria inversa

Esempio 1 (simmetria di un punto):

 

Cordinate di

Esempio 2 (simmetria di una retta):

Simmetria avente la bisettrice del 1° e 3° quadrante come asse di simmetria

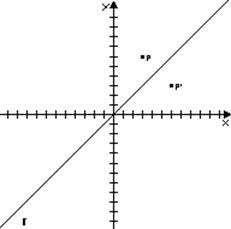
Questa simmetria ha una sua equazione della simmetria che e:

 Equazione della simmetria inversa

Esempio 1 (simmetria di un punto):

 Cordinate di

Esempio 2 (simmetria di una retta):

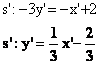
Simmetria avente la bisettrice del 2° e 4° quadrante come asse di simmetria

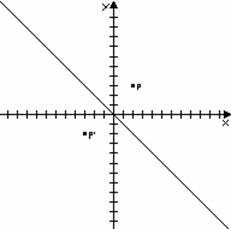Questa simmetria ha una sua equazione della simmetria che e:

 Equazione della simmetria inversa

Esempio 1 (simmetria di un punto):

 

Cordinate di

Esempio 2 (simmetria di una retta):

Simmetria con asse di simmetria obliquo

Da ricordare:  

Due rette sono ortogonali se il coefficiente angolare (k) di una retta è l'antireciproco del coefficiente angolare dell'altra retta.

Condizione 1)       e

           Quindi

         

Condizione 2)  e

           Quindi

         

Mettendo le due condizione in un sistema si ottiene:

Esempio 1 (simmetria di un punto):

Cordinate di

Esempio 2 (simmetria di una retta):