|
|
| |
AFFINITA' IN UN PIANO
Consideriamo un piano p e su di esso un sistema di coordinate cartesiane ortogonali Oxy (ai fini di quello che diremo in questo paragrafo tale ipotesi non è necessaria, ma noi la facciamo per il semplice motivo che siamo abituati a lavorare esclusivamente con tali sistemi di coordinate).
Definizione: Si chiama affinità nel piano p una corrispondenza biunivoca del piano in sé che ad ogni punto P(x,y) associa il punto P le cui coordinate, X e Y sono date da:
![]()
dove a, b, c, d, p, q sono costanti reali
e![]()
La matrice A=![]() si chiama matrice dell'affinità. Le (1) si chiamano equazioni
dell'affinità.
si chiama matrice dell'affinità. Le (1) si chiamano equazioni
dell'affinità.
Per quanto detto un'affinità T è una
corrispondenza invertibile. Si può dimostrare che la corrispondenza inversa,
quella che alla coppia (X,Y) associa la coppia (x,y), che indichiamo con T![]() è anch'essa un'affinità.
è anch'essa un'affinità.
Per le affinità valgono le seguenti proprietà (teoremi):
In un'affinità ad una retta corrisponde una retta (o equivalentemente, a tre punti allineati corrispondono tre punti ancora allineati).
In un'affinità a rette parallele corrispondono rette parallele.
In un'affinità a rette incidenti corrispondono rette incidenti.
In un'affinità è costante il rapporto delle aree corrispondenti.
Tale rapporto si chiama rapporto d'affinità e si può dimostrare che esso è uguale al valore assoluto del determinante della matrice A del 717b15h l'affinità.
Si danno inoltre le seguenti definizioni:
Definizione: Un'affinità di equazioni (1) e matrice A è detta
positiva, o diretta, se det(A)>0; negativa, o inversa, se det(A)<0.
Definizione: Un punto (x,y) si dice unito in un'affinità se è il corrispondente (o immagine o trasformato) di se stesso, cioè se risulta
X=x, Y=y.
Se un'affinità possiede un solo punto unito tale punto è detto centro dell'affinità.
Definizione: Una retta si dice unita (o invariante o fissa) in un'affinità se è la corrispondente di se stessa. Inoltre, se è luogo di punti uniti si dice puntualmente unita ( o puntualmente invariante o puntualmente fissa); altrimenti si dice globalmente unita (o globalmente invariante o globalmente fissa).
Definizione: Una proprietà di una figura F si dice invariante per una trasformazione se essa risulta verificata anche dalla figura F (o, come suol dirsi, si conserva nella figura F ) corrispondente di F tramite la trasformazione.
Qui di seguito elenchiamo le proprietà invarianti per un'affinità:
L'allineamento di tre punti (pertanto un'affinità trasforma rette in rette).
Il parallelismo (pertanto un'affinità trasforma rette parallele in rette parallele, senza peraltro conservare la direzione).
L'incidenza (pertanto un'affinità trasforma rette incidenti in rette incidenti, senza peraltro conservare l'ampiezza degli angoli).
Il punto medio (pertanto il punto medio M di un assegnato segmento AB avrà come immagine, tramite l'affinità, un punto M che risulterà essere punto medio del segmento A B immagine, tramite l'affinità del segmento AB).
Riportiamo alcuni esempi di proprietà che non sono invarianti:
Distanza fra due punti (o equivalentemente, lunghezza di un segmento).
La direzione.
L'ampiezza degli angoli.
Possiamo pertanto affermare che un'affinità non conserva né le dimensioni (poiché non conserva la lunghezza) né la forma (poiché non conserva gli angoli).
Inoltre mentre è vero che in un'affinità è costante il rapporto delle aree di figure corrispondenti, non risulta, in generale, costante il rapporto di segmenti corrispondenti. Tuttavia, se due segmenti sono paralleli e hanno un certo rapporto, allora anche i loro segmenti corrispondenti hanno lo stesso rapporto; così se AB è parallelo a CD ed il loro rapporto vale k, anche il rapporto fra i segmenti corrispondenti A B e C D dovrà valere k.
Infine diamo la seguente definizione:
Definizione: Si chiamano proprietà affini quelle proprietà delle figure che si conservano nelle loro immagini ottenute mediante un'affinità.
Anticipiamo che esistono particolari affinità per le quali è costante il rapporto di due qualsiasi segmenti corrispondenti; tali affinità prendono il nome di similitudini. In virtù di quanto affermato si può dire che l'insieme delle similitudini è un sottoinsieme (proprio) di quello delle affinità.
Vogliamo provare con un esempio che un'affinità conserva il rapporto fra due segmenti paralleli (ovvero il rapporto fra segmenti paralleli è un' invariante per un'affinità). A tal fine consideriamo l'affinità di equazioni:
![]()
e due segmenti paralleli AB e CD di estremi A(0,0), B(1,2), C(-1,1),
D(2,7). Si verifica facilmente che A'(1,-1), B'(0,3), C'(-1,-2), D'(-4,10) e
che ![]() =
=![]() =
=![]() .
.
Inoltre vogliamo segnalare un'altra proprietà delle affinità:
un'affinità diretta conserva il verso di percorrenza;
un'affinità inversa non conserva il verso di percorrenza.
Per convincersene basta disegnare tre punti A, B, C e i loro corrispondenti A', B',C' nell'affinità in esame e verificare che il verso di percorrenza ABC è lo stesso di quello A'B'C' se l'affinità considerata è diretta, mentre è l'opposto nel caso in cui tale affinità è un'affinità inversa.
SIMILITUDINI NEL PIANO
Definizione: Si chiama similitudine piana un'affinità che trasforma una circonferenza in una circonferenza.
Si può dimostrare la seguente proprietà che caratterizza le similitudini piane:
Teorema: Un'affinità è una similitudine se e soltanto se è costante il rapporto di due segmenti corrispondenti (rapporto di similitudine).
E' inoltre importante il seguente teorema:
Teorema: In un sistema cartesiano ortogonale, le equazioni di una similitudine sono del tipo:
![]() oppure del
tipo (2)
oppure del
tipo (2) ![]()
dove k, , p, q sono costanti reali e k>0.
Commento-dimostrazione: a tale risultato si giunge a partire dalle equazioni di un'affinità
![]()
imponendo che l'immagine della circonferenza
di equazioni X![]() +Y
+Y![]() =1 sia ancora una circonferenza; ciò si verifica se e
soltanto se valgono le seguenti relazioni:
=1 sia ancora una circonferenza; ciò si verifica se e
soltanto se valgono le seguenti relazioni:
(*) 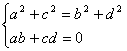
che rappresentano le condizioni analitiche cui debbono soddisfare i coefficienti di un'affinità per essere una similitudine.
Posto k = ![]() , si può scrivere a =
kcos
, si può scrivere a =
kcos![]() e c = ksen
e c = ksen![]() ; sostituendo le espressioni di a e c appena trovate nel
sistema (*) si ottiene il sistema equivalente:
; sostituendo le espressioni di a e c appena trovate nel
sistema (*) si ottiene il sistema equivalente:
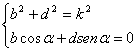
Risolvendo tale sistema rispetto a b e d si ottengono le soluzioni:
![]() e
e ![]()
Sostituendo nelle (3) ad a, b, c, d i valori ora trovati si ottengono le (1) e le (2).
Il numero reale positivo k = ![]() =
= ![]() che compare nelle
equazioni (1) e (2) di una similitudine prende il nome di rapporto di
similitudine.
che compare nelle
equazioni (1) e (2) di una similitudine prende il nome di rapporto di
similitudine.
Esso rappresenta il rapporto costante tra segmenti corrispondenti in una similitudine (tale proprietà può essere facilmente dimostrata).
Poiché risulta a = kcos e c = ksen , le equazioni della similitudine assumono la forma:
) ![]() oppure (2 )
oppure (2 ) ![]()
essendo k = ![]() il rapporto di
similitudine.
il rapporto di
similitudine.
Nelle (1 ) risulta det(A) = a![]() >0, mentre nelle (2 ) risulta det(A) = a
>0, mentre nelle (2 ) risulta det(A) = a![]() <0. Pertanto le (1 ) rappresentano le equazioni di una similitudine diretta di
rapporto k =
<0. Pertanto le (1 ) rappresentano le equazioni di una similitudine diretta di
rapporto k = ![]() , mentre le (2 ) rappresentano le equazioni di una similitudine inversa di
rapporto k =
, mentre le (2 ) rappresentano le equazioni di una similitudine inversa di
rapporto k = ![]() .
.
Qui di seguito elenchiamo le proprietà invarianti per una similitudine:
Tutte le proprietà invarianti per un'affinità.
Ampiezza degli angoli.
Inoltre una similitudine conserva il rapporto tra segmenti corrispondenti. Tale rapporto costante k, come già detto, prende il nome di rapporto di similitudine. Da questa proprietà discende in modo ovvio che in una similitudine è costante il rapporto dei perimetri di due figure corrispondenti (dette figure simili) e tale rapporto è pari al rapporto di similitudine k.
Elenchiamo alcune proprietà che non sono invarianti per una similitudine:
Distanza fra due punti (o equivalentemente, lunghezza di un segmento).
Direzione.
Per quanto detto si può affermare che le similitudini non conservano le dimensioni (poiché non conservano la distanza) ma conservano la forma (poiché conservano l'ampiezza degli angoli).
OMOTETIE
Se nelle equazioni (1) di una similitudine poniamo α=0 otteniamo:
![]() ;
;
tali equazioni rappresentato le equazioni di una omotetia a patto che la trasformazione da esse rappresentata abbia uno ed un solo punto unito; ciò accade, come facilmente si verifica sse , risulta k 1 (e anche k>0 trattandosi di una similitudine); infatti:
![]()
![]()
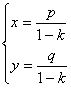 dunque la
trasformazione considerata ammette uno ed un solo punto unito sse 1-k 0, ovvero sse k
dunque la
trasformazione considerata ammette uno ed un solo punto unito sse 1-k 0, ovvero sse k
Se invece risulta k=1 allora le equazioni (3), come facilmente si comprende, rappresentano una traslazione (trasformazione priva di punti uniti) di vettore v(p,q) se almeno uno fra i valori di p e q è diverso da zero (se p vel q 0), l'identità (o trasformazione identica ).avente come punti uniti: tutti i punti del piano se p=q=0.
Riepilogando possiamo dire che le equazioni
![]()
con k>0 e k 1 rappresentano un'omotetia di centro C![]() (il centro di un'omotetia è il suo unico punto unito) e
rapporto k. Tale omotetia essendo stata ricavata da una similitudine diretta è
una omotetia diretta. Il numero k, detto rapporto di omotetia rappresenta il
rapporto costante fra segmenti corrispondenti.
(il centro di un'omotetia è il suo unico punto unito) e
rapporto k. Tale omotetia essendo stata ricavata da una similitudine diretta è
una omotetia diretta. Il numero k, detto rapporto di omotetia rappresenta il
rapporto costante fra segmenti corrispondenti.
Se invece nelle equazioni (1) di una similitudine poniamo α=π otteniamo:
![]() ;
;
posto h= k le (4) diventano:
(5) ![]()
con h<0 (essendo k>0 poiché rapporto di similitudine).
Tali equazioni rappresentano le equazioni di una omotetia a patto che la trasformazione da esse rappresentata abbia uno ed un solo punto unito; ciò accade, come facilmente si verifica, per ogni valore negativo di h (cioè sempre); infatti:
![]()
![]()
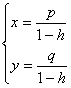 dunque la trasformazione
considerata ammette uno ed un solo punto unito sse 1 h ovvero sse h 1, ma ciò
accade sicuramente essendo nelle (5) h<0. Anche in questo caso l'omotetia,
essendo stata ricavata da una similitudine diretta, è una omotetia diretta di
rapporto k= h. Tale rapporto, come al solito,
rappresenta il rapporto costante fra due segmenti corrispondenti.
dunque la trasformazione
considerata ammette uno ed un solo punto unito sse 1 h ovvero sse h 1, ma ciò
accade sicuramente essendo nelle (5) h<0. Anche in questo caso l'omotetia,
essendo stata ricavata da una similitudine diretta, è una omotetia diretta di
rapporto k= h. Tale rapporto, come al solito,
rappresenta il rapporto costante fra due segmenti corrispondenti.
Mentre le (4) definiscono un'omotetia che ad un punto P diverso dal suo centro O fa corrispondere un punto P' che si trova dalla stessa parte di P rispetto ad O, le (5) definiscono un'omotetia che ad un punto P diverso dal suo centro O fa corrispondere un punto P' che si trova dalla parte opposta di P rispetto ad O. Ecco perché talune volte si usa dire, impropriamente, che le omotetie di equazioni (4) sono omotetie dirette, mentre quelle di equazioni (5) sono omotetie inverse.
Ribadiamo invece che le omotetie sono sempre dirette (essendo particolari similitudini dirette), pertanto conservano l'orientamento.
Le omotetie con k>1 e quelle con h< 1 sono degli "ingrandimenti", quelle con 0<k<1 e quelle con 1<h<0 sono delle "riduzioni".
Osserviamo infine che se nelle (5) poniamo h= 1 otteniamo:
(6) ![]()
che sono le equazioni di una simmetria
centrale il cui unico punto unito è il centro C![]() .Alla luce di quanto deto possiamo afermare che le simmetrie
centrali sono delle particolari omotetie di rapporto k=1 (rapporto costante fra
segmenti corrispondenti) e che come tutte le omotetie sono delle trasformazioni
dirette (conservano cioè l'ordinamento).
.Alla luce di quanto deto possiamo afermare che le simmetrie
centrali sono delle particolari omotetie di rapporto k=1 (rapporto costante fra
segmenti corrispondenti) e che come tutte le omotetie sono delle trasformazioni
dirette (conservano cioè l'ordinamento).
ISOMETRIE NEL PIANO
Definizione: Si chiama isomeria (o congruenza o movimento rigido) piana ogni similitudine di rapporto 1.
Ponendo nelle equazioni (1) e (2) delle similitudini k=1 si hanno le isometrie, rispettivamente, dirette e inverse.
Per k=1 le (1) diventano:
(7) ![]()
che sono le equazioni delle isometrie dirette o rototraslazioni.
Per α=0 si ha la traslazione:
(8) ![]() .
.
Per p=q=0 si ha la rotazione:
(9) ![]()
con il centro nell'origine delle coordinate e ampiezza α.
Per α=π , dalle (9) si hanno le equazioni della simmetria centrale di centro O:
(10) ![]() .
.
Per k=1 le (2) diventano:
(11) ![]()
che sono le equazioni delle isometrie inverse.
Per p=q=α=0 le (11) ci danno:
(12) ![]()
che sono le equazioni della simmetria assiale di asse x.
Per p=q=0 e α=π le (11) ci danno invece:
(13) ![]()
che sono le equazioni della simmetria assiale di asse y.
Osservazione: Per quanto detto risulta chiaro che le equazioni:
(14) ![]()
individuano un'isometria sse
(15) 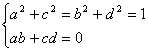 .
.
e che :
se ![]() =1, l'isometria è diretta;
=1, l'isometria è diretta;
se invece ![]() = 1, l'isometria è inversa.
= 1, l'isometria è inversa.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024