|
|
| |
DIAGRAMMI DI FASE
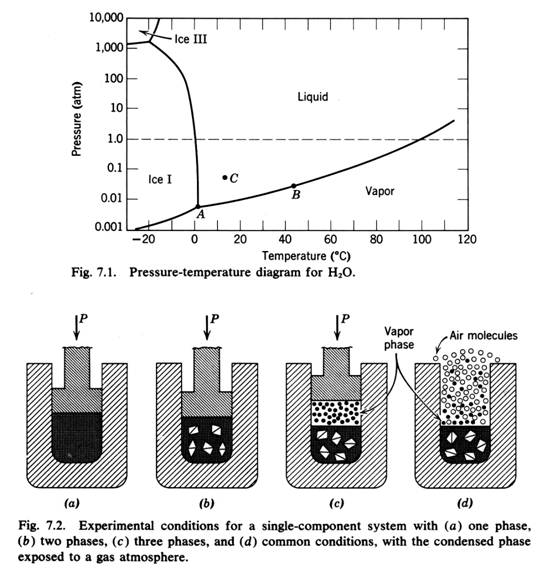
Fase : Parte del sistema con proprietà omogenee in tutta la sua estensione separato dalle altre da una interfaccia.
Un sistema è in equilibrio a T e P costanti quando G è minima
G = H -TS
Analogamente si può dimostrare che un sistema è in equilibrio quando
U è minima a S e V costanti
H è minima a S e P costanti
A è minima a T e V costanti
Consideriamo un cristallo in equilibrio con il suo vapore
A = U -TS
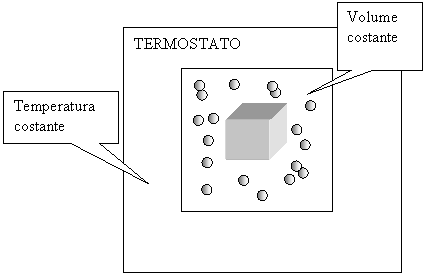
A sarà minima quando U è piccola e TS è grande
Le forze attrattive tendono a far condensare il vapore
U diminuisce
q viene trasferito al termostato.
Se il processo fosse completo U sarebbe minima ma anche S sarebbe bassa.
S= k ln W e W è più piccola per la disposizione ordinata del cristallo che per il gas.
Se il cristallo evaporasse completamente
U sarebbe massima
Il disordine sarebbe massimo .. S massima
q viene assorbito dal termostato.
Calcolando U e S mediante metodi della meccanica statistica
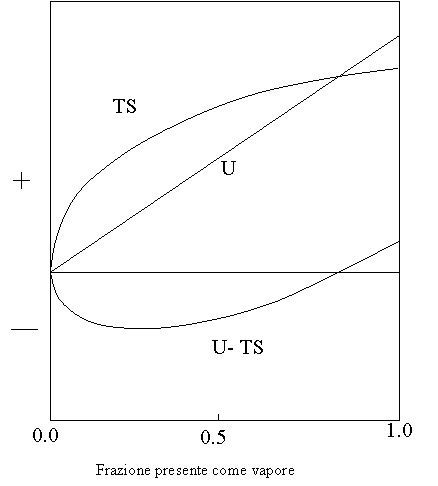
Il valore minimo di A si ottiene quando una certa frazione della sostanza è presente in fase vapore.
La pressione a cui si trova in equilibrio si chiama TENSIONE DI VAPORE.
Lo stato di equilibrio del sistema è un "compromesso" tra ordine e disordine.
Per il sistema isolato complessivo ( cristallo + termostato) è ancora vero che l'entropia tende ad un valore massimo
Equilibrio di trasferimento tra le fasi
![]()
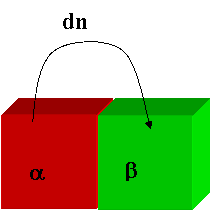
dG =-SdT+VdP+ S midni
A temperatura costante
dG = S dG = S VfdPf.+ (mib mia dnia
A pressione costante
dG = (mib mia dnia
Un sistema a P,T costante è in equilibrio se dG = 0
mib mia
La condizione di equilibrio fra più fasi è quindi che il potenziale chimico di ogni sostanza abbia lo stesso valore in tutte le fasi fra le quali può passare liberamente
REGOLA DELLE FASI
Due fasi in equilibrio devono avere
Stessa Temperatura
Stessa Pressione
Ogni sostanza contenuta nelle fasi deve avere lo stesso potenziale chimico
Per una sostanza pura
Lo stato del sistema è completamente determinato se si conoscono : Ta ,Tb Pa ePb
Ma in condizioni di equilibrio devono sussistere le relazioni :
Ta = Tb
Pa = Pb
ma (Ta,Pa mb (Tb,Pb
Ne consegue che una sola delle quattro variabili può essere scelta arbitrariamente
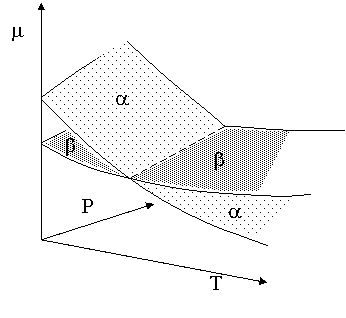
Ta = Tb
Pa = Pb
ma (Ta,Pa mb (Tb,Pb
Le tre relazioni sono soddisfatte lungo la linea tratteggiata !
La proiezione dell' intersezione delle due superfici sul piano P T è la linea della tensione di vapore.
Sistema a più componenti ( che non reagiscono fra loro)



Per fissare la composizione di ciascuna fase sono sufficienti C-1 variabili
(Es. Xi , Ci , ni), comprendendo anche temperatura e pressione ( +2)
Numero totale delle variabili = F ( C + 1)
Relazioni tra le variabili
Ta = Tb = Tg = .......... (F-1) eguaglianza di temperatura
Pa = P b = P g = ........ .. (F-1) eguaglianza di pressione
m1a m1b = m 1g = ......(F-1) eguaglianza di m per la specie 1
m2a m2b = m 2g = ......(F-1) eguaglianza di m per la specie 2
Numero delle equazioni (F-1) (C+2)
I potenziali di una fase mista sono funzione delle C-1 variabili.
mia (Ta,Pa, x1a, x2a, .., x(c-1) a mib (Tb,Pb, x1b, x2b, .., x(c-1) b
Il numero delle relazioni non può essere superiore al numero delle variabili,( in caso contrario alcune equazioni sarebbero incompatibili).
F ( C + 1) ≥ (F-1) (C+2)
C+2 - F>0
Il numero delle fasi in equilibrio fra loro non può essere maggiore del numero dei componenti + 2.
( cfr punto triplo dell'acqua)
Sottraendo il numero delle equazioni dal numero delle variabili si ottiene il numero delle variabili del sistema (V ) che possono essere scelte liberamente dallo sperimentatore.
F ( C + 1) - (F-1) (C+2) = V
V= C+2-F
V viene detta anche varianza o numero di gradi di libertà del sistema
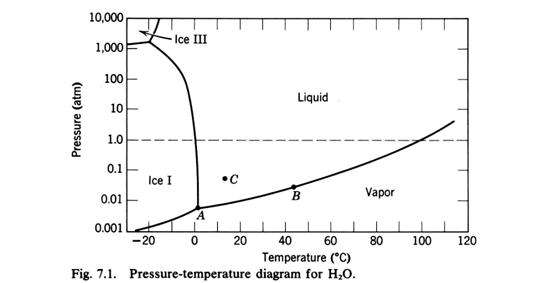
Esempi di applicazione della regola delle fasi
1 Solo vapore varianza ?
2. Vapore più una sola fase liquida
3 Vapore + liquido+ solido
Clausius-Clapeyron
È noto che nelle trasformazioni di fase
Solido liquido gas
Avvengono a T e P costanti con assorbimento di calore
Per la trasformazione acqua vapore a
q = DU +w
il 92% va speso in aumento dell'energia interna
Cinetica (traslazionale, vibrazionale, rotazionale)
Potenziale ( aumento della distanza tra le molecole)
DH = DU + D(PV)
Indicando con h l'entalpia molare ci si può attendere che
hs<hl<hg
Ws<Wl<Wg
ss<sl<sg
con s minuscolo si indica l'entropia molare
Fissati i valori di temperatura e pressione la fase più stabile è quella che ha il potenziale chimico ( o l'energia libera di Gibbs molare g) più basso.
Per es. il liquido è più stabile se
ml<mg
(hl-Tsl) < (hg-Tsg)
T (sg-sl) < (hg-hl)
Viceversa il vapore è più stabile se
T (sg-sl) > (hg-hl)
L'equilibrio tra due fasi è determinato da un compromesso tra il fattore energetico e quello entropico. La transizione liquido vapore è resa possibile dall'aumento dell'energia disponibile
L'equazione di Clausius-Clapeyron
Sistema ad un componente due fasi a e b
ma mb
ma + d ma mb + d mb
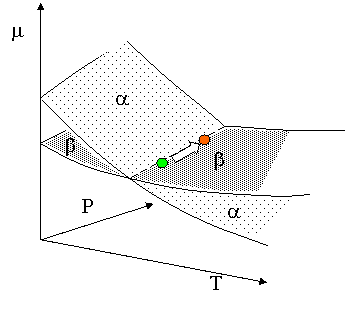
d ma d mb
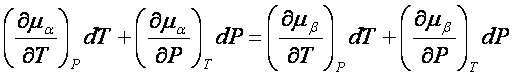
Esprime la relazione che esiste fra una variazione di temperatura dT e una simultanea variazione dP in modo tale da mantenere l'equilibrio tra la fasi.
- Sa dT + Va dP = - Sb dT + Vb dP
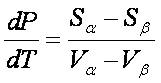
all'equilibrio i potenziali chimici sono uguali la transizione di fase è reversibile
(sa - sb ) = L/T = (ha - hb ) / T
L calore latente di evaporazione
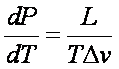
Determina l'aumento di pressione dP necessario a mantenere l'equilibrio di fase se la temperatura aumenta di dT. ( pendenza nel diagramma Temperatura / Pressione)
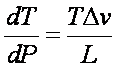
effetto della pressione sulla temperatura della transizione di fase
Trascurando il volume molare del liquido
Dv = vg = RT/P
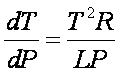
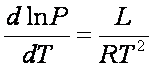
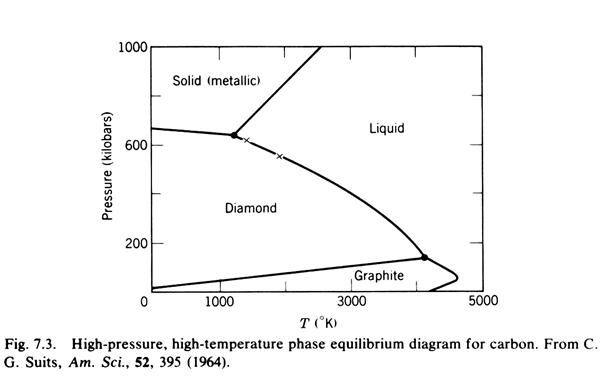
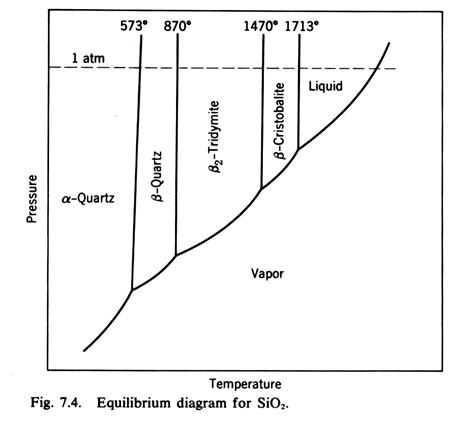
ALLOTROPIA
![]()
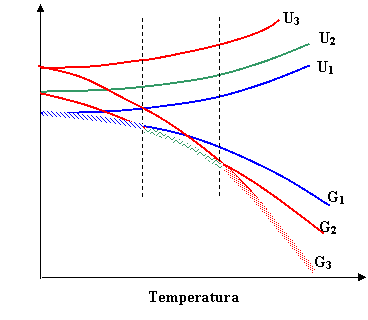
Relazioni tra l'energia interna U e l'energia libera di Gibbs di diverse forme allotropiche (polimorfismi) U1<U2<U3 e S1<S2<S3
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026