|
|
| |
Leggi costitutive e definizioni
Lo sforzo di deformazione che mantiene le particelle a velocità differenti, opponendosi all'attrito viscoso, è pari a una forza su unità di area, che è la sezione per cui passa il fluido:
τ = F/A (τ = 0 se campo di velocità è uniforme non c'è attrito viscoso)
Esso è proporzionale alla variazione delle velocità lungo un eventuale ascissa y, tale per cui v=0 sulle pareti e massima al centro della sezione, la costante di proporzionalità è detta viscosità dinamica:
τx = μ dvx/dy dv/dy = ° LEGGE DI NEWTON: τ = μγ°
Proprietà fisiche dei fluidi
Densità: ρ = dm/dV [kg m-3] nei gas perfetti: ρ = P / RxT
Volume specifico: V* = dV/dm = 1/ρ [m3 kg-1] su massa
V° = V/n = RuT/P [m3 kmol-1] su n moli
Per miscele di gas: V* = Σωi V*i con ω = frazione massiva
Peso specifico: γ = mg/V = ρg [N m-3]
Viscosità dinamica: μ = τ/γ° [Pa s] indica quanto è forte lo sforzo di deformazione in funzione dell'aumento delle velocità relative di scorrimento
μ = μ(T, P) la viscosità dipende da T e P: nei gas è direttamente proporzionale, nei liquidi è inversamente proporzionale a T.
gas: μg = μg(T riferimento) (T/Trif)α
liquidi: μl = μl(T riferimento) exp[(1/T - 1/Trif) β] con α e β costanti e T in Kelvin
Modulo di comprimibilità
k = -V* dP/dV* = ρ dP/dρ [Pa] definisce la comprimibilità di un fluido
gas perfetti: compressione isoterma: P = RuT/V° k = -V° (-RuT/V°2) = RuT/V° = P
tras. adiabatica isoentropica: PV°γ = cost, con γ = Cp°/Cv° k = γP
liquidi: ho leggi empiriche (es acqua) V*(T P) = V*o [1+λ(T-To+aP)2-koP]
con V*o = 1,00008 10-3 m3/kg , λ = 8 10-6 1/K2 , a = 2 10-7 Pa/K , To = 277°K
ottengo: k = [1+ (T-To+aP)2-koP] / [ko - 2a (T-To+aP)] = 2,0003 109 Pa
Tensione superficiale = forza per unità di lunghezza, è dovuta al fatto che le forze idrostatiche al pelo libero non sono bilanciate. Se considero una bollicina tagliata di traverso, devo avere che la forza esterna è bilanciata da quella interna:
ΔP πr2 = σ 2πr ΔP = 2σ/r per un cilindro: ΔP = σ/r
l'effetto della tensione superficiale è importante per raggi piccoli; ad esempio, per le bolle di vapore in un liquido, se ΔP supera la tensione di vapore, la bollicina collassa.
Capillarità: θ = bagnabilità, è l'angolo che si forma tra il menisco e i bordi del capillare. L'equilibrio statico impone che la spinta verso l'alto dovuta alla tensione superficiale Fσ , sia bilanciata dal peso della colonna di liquido sollevata:
σ cosθ π d = ρ g π/4 d2 H H = 4 σ cosθ / ρ g d risalita capillare
Tensione di vapore: Nel piano P/T rappresenta il luogo dei punti che tra il punto triplo e il punto critico separa liquido da gas, esprime la volatilità di una sostanza.
Statica dei fluidi
Isotropia della pressione: considero un triangolo rettangolo e forze agenti su cateto x (py), sul cateto y (px) e sull'ipotenusa s (ps) e una forza peso pari a ρg dxdy/2 = γ dxdy/2 diretta verso la parte negativa delle ascisse. Le equazioni della statica sono:
Rx = 0 pxdy - psds senθ = 0
Ry = 0 pydx - psds cosθ - γ dxdy/2 = 0
Essendo ds cosθ = dx e ds senθ = dy, ottengo:
(px - ps)dy = 0
(py - ps)dx - dxdy/2 = 0
Mandando al limite dx e dy a 0 ottengo px = py = ps per qualunque angolo θ
Campo di pressione: δP/δz = -ρg EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI
Mentre le derivate parziali x e y sono uguali a 0 perché P varia solo in funzione della quota.
Integrando ottengo P(z) = P(z1) - ρg (z - z1) che mi indica la variazione di P da una quota conosciuta z1 a una quota qualsiasi z.
Pressione in termini di altezza liquida: H = P/ρg = P/γ se soddisfatta, ovvero ρ è costante, si parla di campo di pressione idrostatico.
Nei gas perfetti: ρ = P/RxT dP/dz = -P/RxT (equazione differenziale)
dP/P = -g/RxT dz integro ln(P/Po) = -g(z-zo)/RxT = -ρg(z-zo)/Po
P = Po exp(-ρg(z-zo)/Po)
Forze su superfici consideriamo un diga inclinata di un angolo α con la verticale, sia η la profondità, Y le
contenenti fluidi: coordinate lungo la linea verticale della diga e X lungo il bordo di essa. Se scegliamo una superficie arbitraria A, ad una qualsiasi quota η si avrà una spinta pari a Fext + Fint:
dF = -PodA + (Po + γη)dA = γηdA
detto S il baricentro di A, F = γηsA che rappresenta il modulo di F. Il suo punto di applicazione però non coincide con S, bensì col centro di spinta M. Se riscriviamo F secondo le coordinate della diga X e Y, tale che S coincide con Ys e η = Ycosα, ottengo:
F = γηsA = γAYscosα dF = γYcosα
M è identificato ponendo le componenti del momento della forza F, rispetto a x e a y, siano le stesse dei momenti distribuiti sulla superficie A:
F XM = ∫A x dF = ∫A γ cosα x y dA con F = γYcosα
F YM = ∫A y dF = ∫A γ cosα y2 dA semplifico γ cosα e ottengo
XM = [ ∫A xy dA ] / A Ys
YM = [ ∫A y2 dA ] / A Ys integrali doppi da risolvere in dx e dy Affondamento: e = YM - YS considero superficie rettangolare di altezza h, larghezza b, affondata di Δ al pelo libero. Y parte dal pelo libero, X è il pelo libero, O è posto a metà in modo che Y tagli la base b in b/2.
A = hb YS = Δ + h/2
XM = [ ∫A xy dA ] / A Ys = -b/2∫+b/2 x dx Δ∫Δ+h y dy = 0 [y3/3]ΔΔ+h / AYS = 0
YM = [ ∫A y2 dA ] / A Ys = -b/2∫+b/2 dx Δ∫Δ+h y2 dy = b [y3/3]ΔΔ+h / AYS =
b/3 [(Δ+h)3 - Δ3] / hb (Δ+h) = [(Δ+h)3 - Δ3] / [3h(Δ+h)]
e = YM - YS = [(Δ+h)3 - Δ3] / [3h(Δ+h)] - (Δ+h) = h2/12(Δ+h) >0 sempre
se Δ = 0 YM = 2/3 h YS = 1/2 h e = 1/6 h
quindi F = γAYs ma è applicata in YM, quindi il momento rispetto a O: M = γAYSYM
Forze su superfici P è uniforme, F = ∫PdA = PA = γhA applicata nel baricentro della superficie.
orizzontali:
Forze su superfici curve: Considero superficie curvilinea, X e Y indicano il piano del pelo libero, Z la profondità.
Su dA agisce dF = γzdA normale alla superficie. Gli angoli tra dA e i piani YZ, XZ, XY sono rispettivamente λ, μ, υ. Le proiezioni sugli assi di dA sugli assi sono:
dAx = dA cosλ dAy = dA cosμ dAz = dA cosυ
Le componenti di dF:
dFx = γzdAx dFy = γzdAy dFz = γzdAz e integro in A.
La componente verticale di F è uguale al peso della colonna di fluido sovrastante: ∫dFz = γV
Dinamica dei fluidi
In un sistema di coordinate cartesiane x,y,z ogni particella al tempo t ha una velocità v che dipende dal punto considerato P e dal tempo t. Si ha un campo di moto esteso a tutta la regione di spazio occupata dal fluido. Se il vettore velocità in A non è in funzione del tempo si parla di campo di moto stazionario, altrimenti dinamico o transitorio.
v = v(P, t) = (u i , v j , w k)
Descrizione Lagrangiana: Considero una porzione di fluido dm e ne descrivo il moto:
a t0 dm è in P0 (x0, y0, z0)
a t>0 dm è in P = P (P0, t) = [X(x0, y0, z0, t), Y(x0, y0, z0, t), Z(x0, y0, z0, t)]
P - P0 = vettore spostamento, v = dP/dt = vettore velocità
Descrizione Euleriana: Considero un campo di velocità e v in funzione della posizione P e del tempo t:
v = [vx(x, y, z, t), vy(x, y, z, t), vz(x, y, z, t)] = v(P, t)
dv/dt = accelerazione sostanziale = [dvx/dt, dvy/dt, dvz/dt]
le componenti dell'accelerazione si ottengono: dvx/dt = δvx/δx + δvy/δy + δvz/δz + δv/δt
Flussi unidirezionali: La superficie di fluido che non è attraversata dal fluido stesso è dette linea di flusso ed è tangente in ogni punto a v. Un insieme di linee di flusso costituisce un tubo di flusso.
Tubi di corrente Per ipotesi consideriamo ρ costante. Considero un elemento di fluido che passa per due
monodimensionali: sezioni diverse S e S'. m = cost t1 = t t2 = t+dt
la legge di conservazione della massa ci dice che ρ1v1A1 = ρ2v2A2 e siccome la densità è costante passo alla legge di conservazione della portata volumetrica v1A1 = v2A2. Per fluidi molto comprimibili devo tener conto del possibile accumulo di massa nel volume di controllo: d[∫SρdV]/dt = ρ1v1A1 - ρ2v2A2
Equazioni euleriane del Consideriamo un fluido non viscoso soggetto solo alla forza della gravità. Facciamo
moto riferimento ad un tubo di corrente di lunghezza ds lungo il flusso e sez. dA ortogonale a ds.
Sia φ l'angolo tra ds e la coordinata verticale negativa.
dm dv/dt = ∑F dm = ρdsdA v = velocità lungo la coordinate A.
Le forze applicate sono la componente nella direzione S della forza peso:
dFg = g dm cosφ = g ρ ds dA cosφ
la differenza di pressione tra le facce superiore e inferiore del volume del fluido:
dFP = -δP/δs ds dA
ottengo quindi: ρ ds dA dv/dt = g ρ ds dA cosφ -δP/δs ds dA
sostituisco cosφ = -δz/δs e ottengo l'accelerazione lungo la coordinata S di v:
dv/dt = -g δz/δs - 1/ρ δP/δs
Inoltre, essendo dv/dt = δv/δs ds/dt + δv/δt = δv/δt + v δv/δs = δv/δt + ½ δv2/δs
Componendo le due equazioni ottengo la 1A EQUAZIONE DI EULERO:
δv/δt + ½ δv2/δs + g δz/δt + 1/ρ δP/δs = 0 lungo la coordinata S tangente al flusso.
Se ora considero l'accelerazione trasversale, quindi come varia v in funzione della posizione lungo la sezione di tubo, dia dn la lunghezza e dA' la sezione del volume di controllo. Sia φ' l'angolo tra dn e la coordianata verticale negativa (rispetto a prima dn è perpendicolare a ds).
dm [δun/δt + v2/R] = ∑F con R = raggio di curvatura cosφ' = δz/δs
operando in modo analogo a prima so che le forze in gioco sono:
Fg = -g ρ dn dA'cosφ' FP = - δP/δn dn dA'
Ottengo la 2A EQUAZIONE DI EULERO
δun/δt + v2/R = -g δz/δn - 1/ρ δP/δn lungo la coordinata N perpendicolare al flusso.
Equazione di Bernoulli: Equazione della piezometrica: la somma delle tre altezze rimane costante lungo una linea di
flusso: v2/2g + z + P/ = cost [m]
Misuratore di portata come calcolare la portata volumetrica V/s = Q dalla differenza di pressione dovuta al
Venturi: restringimento di sezione: considero un tubo di sezione A1, che si riduce alla sezione A2, per poi tornare alla sezione iniziale. Vengono misurate le pressioni del fluido in A1 e in A2:
Bilancio di materia: ρv1A1 = ρv2A2
Bernoulli: v12/2g + P1/γ = v22/2g + P2/γ
Ottengo:v1 = v2 A2/A1 (P2-P1)/γ = v22/2g [(A2/A1)2 -1] v2 = √[2g (P2-P1)/γ]/ [(A2/A1)2 -1]
Concludo: Q = v2A2 = A2 √[2g (P2-P1)/γ]/ [(A2/A1)2 -1]
Efflusso sotto battente: Considero un serbatoio riempito fino altezza h. Alla base vi è un foro di sezione A, che a causa della contrazione di vena diminuisce nel calcolo a: A = Cc A.
v12/2g + P1/γ + h = v22/2g + P2/γ + 0 v2 = √[v12 + 2g [(P1-P2)/γ + h]]
in genere v2>v1 v22/2g >>> v12/2g quindi elimino v12/2g
inoltre P1 = P2 = Patm elimino anche P1-P2
ottengo la Velocità Torricelliana di efflusso: v = √[2gh]
Pertanto la portata volumetrica è pari a: Q = vA = √[2gh] Cc A
Nel caso in cui il foro sia talmente grande da giustificare una differenza nelle velocità di uscita all'interno della stessa sezione, si fa una media di v:
<v2> = 1/A ∫A v dA = 1/Asenφ h1∫h2 b √[v12 + 2gz] dz con b = larghezza sezione
Nel caso di parete verticale senφ = 1 si ha:
Q = v Cc A = Cc h1∫h2 b √[v12 + 2gz] dz = Cc b √2g h1∫h2 √[v12/2g + z] dz =
Q = 2/3 Cc b √2g [(v12/2g + h2)3/2 - (v12/2g + h2)3/2]
Stramazzi rettangolari: Considero una "diga" affondata di H dal pelo libero. Se scrivo l'eq. di Bernoulli tra le due sezioni: v12/2g + P1/γ + z1 = v22/2g + 0 + z2 sia H = P1/γ + z1 altezza pelo libero
v2 = √[2g(H - z2 + v12/2g)] Q = Cc b 0∫H v2z2 dz = Cc b 0∫H √2g (H - z2 + v12/2g)1/2 dz2 =
Q = 2/3 Cc b √2g [(v12/2g + H)3/2 - (v12/2g)3/2
In genere la corrente è lenta: v 0, ottengo: Q = 2/3 Cc b √2g H3/2
Altezza di crescita sopra lo stramazzo: Hcr = (3/[2Cc √2g])3/2 (Q/b)3/2
Empiricamente: Hcr = 0,666 (Q/b)3/2 da cui Cc per stramazzi rettangolari: Cc = 0,623
Bilancio della Q di Moto: QdM = P dPtot/dt = ρ1v12S1 - ρ2v22S2 + (P1S1 - P2S2) - F + mtotg [N]
N.B. S1 e S2 sono aree vettoriali: |S|n = area per il suo versore normale.
mtot = ∫ρdV Ptot = ∫ρvdV -F = forza netta esercitata dal fluido su superfici
portate massive vettorializzate: W = |ρvS|norm [kg/s]
dP/dt = -Δ[Wv + PS] -F + mg in condizioni di regime stazionario dP/dt = 0 e ottengo:
F = -Δ[Wv + PS] + mg che è la formula per calcolare la spinta di un fluido su superfici.
Bilancio energia Rimuoviamo l'ipotesi di fluido non viscoso v = <v> media
meccanica: Bernoulli: Δ[½ (<v3>/<v>) + gz + P/ρ] + Ev = 0 [m2/s2 = energia/massa = J/Kg]
Ev = energia dissipata per attrito viscoso piezometrica non costante ma in caduta: cadente.
<vn> = [ 0∫2π dφ 0∫R vn r dr] / πR2 per cui uso:
n=1 per portata fluente, n=2 v = <v2>/v per la QdM, n=3 v = <v3>/<v> per en. cinetica.
Distribuzione di velocità Considero un fluido viscoso che scorre su un piano inclinato: x è la coordinata che misura la
in regime laminare: profondità ed è perpendicolare a z che è posta sul pelo libero. Osserviamo una porzione profonda δ e lunga L: v è diretta lungo asse z e dipende da x = vz (x)
bilancio QdM: LWτx=x - LWτx=x+Δx + WΔxV2z=0 - WΔxV2z=L + LWΔxρgcosβ = 0
Siccome v non dipende da z, il terzo e il quarto termine riferenti all'energia cinetica sono uguali e si annullano. Inoltre sul pelo libero non ho sforzi quindi τx=x = 0
Dividendo tutto per LWΔx e mandando al limite Δx 0 ottengo:
τx=x+Δx/Δx = ρgcosβ dτ/dx = ρgcosβ τ = ρgcosβ x
lo sforzo cresce con la profondità ed è massimo in x = δ
Ma Newton dice: τ = -μdvz/dx e ottengo: dvz/dx = - ρgcosβ x / μ
Integrando ottengo: vz = [ρgcosβ/2μ] x2/2 + C
Le condizioni sono: per x = δ, vz = 0 per l'adesione alle pareti.
vz = [ρgcosβ/2μ] δ2 [1-(x/δ)2] che è massima in x = 0 e nulla in x = δ
La velocità media è: <v> = [0W∫dy 0δ∫ v dx ]/ wδ = vmax 0δ∫[1-(x/δ)2]dx / δ
<v> = vmax 01∫(1-ξ2)dξ con ξ = x/δ = 2/3 vmax = ρgcosβδ2/3μ
La forza esercitata dal fluido sulla parete di scorrimento è:
F = τw W L = ρgcosβδ W L pari alla componente in z del peso del film.
La portata per unità di larghezza Г = W/w con w = larghezza:
Г = ρδ<v> se è nota trovo δ = (3μГ / ρ2gcosβ)1/3
I risultati ottenuti sono validi solo in regime laminare, ovvero se il numero di Reynolds del
Film è inferiore ad un valore critico: Recr = 4δ<v>ρ/μ = 4Г/ρ < 25
Flusso laminare in Considero un tubo di asse z e diametro y, e ne sviluppo il bilancio di QdM in direzione z:
condotto circolare: ![]()
Il terzo e quarto termine si annullano perché v non dipende da z, dividendo tutto per 2πrLΔr e mandando Δr 0 ottengo: d(rτ)/dr = [(Po-PL)/L + ρg]r
Chiamando Ρ = P + ρgz l'altezza piezometrica, e integrando ottengo:
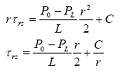
Le
condizioni sono: per r = 0, τ = 0, e allora C = 0 ![]()
Secondo Newton: τ = -μdvz/dx
Ottengo: ![]()
integrando: ![]()
Posso
comunque scrivere: ![]()
La
velocità media vale: 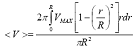 =
= ![]()
I rapporti tra velocità medie reali e aritmetiche vale:
![]()
Il legame tra <v> e τ è:
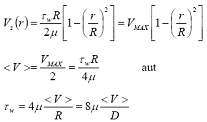
Ma siccome:
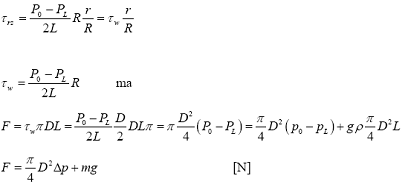
Per cui il primo termine misura la caduta di pressione legata alla viscosità, il secondo il peso del fluido, se il condotto fosse orizzontale vi sarebbero solo perdite di pressione.
Fattore d'attrito: Il rapporto tra la forza appena ottenuta esercitata sul tronco di tubazione e l'area è:
F/A = τ fattore d'attrito: f = τ / ½ρ<v>2
Se introduco l'espressione trovata in precedenza: τ = 8μ <v>/D, ottengo:
f = 16 μ / ρ<v>D = 16/Re laminare per Re < 2100-2350 e turbolento per Re> 104
Sempre all'interno del condotto circolare, la potenza meccanica dissipata vale:
QΔP con Q = portata volumetrica e P = altezza piezometrica = Ρ = P + ρgz
![]()
Riferita alla portata massiva fluente W:
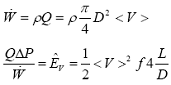
Questo termine si riferisce alle perdite di carico distribuite.
Prima di cambiare argomento, mette conto scrivere, e memorizzare per sviluppi futuri, relazioni alternative, ma equivalenti, per lo scorrimento, a regime, in un tubo cilindrico
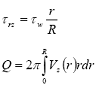
Integrando la seconda relazione (portata) per parti, si ottiene:
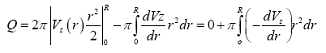
Dalla prima:
![]()
sostituendo la variabile r con la variabile τrz, si può scrivere altresì:
![]()
nel caso, già considerato, di fluido a viscosità newtoniana in regime laminare:
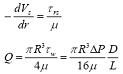
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026