Lezioni di Elettronica digitale - Le porte logiche (parte prima)

elettronica

Lezioni di Elettronica digitale

Le porte logiche (parte prima)

Premessa

Le principali parti elettroniche dei computer sono costituite da circuiti digitali che, come è noto, elaborano segnali logici basati sullo 0 e sull'1.

I mattoni fondamentali dei circuiti logici sono, appunto, le porte logiche che sono in grado di soddisfare un'algebra particolare, detta algebra binaria, sviluppata dallo scienziato George Boole (1815-1864).

In questo semplice articolo si introdurranno le porte logiche fondamentali in grado di svolgere le operazioni di somma, prodotto e negazione indicate, rispettivamente, con OR (somma logica), AND (prodotto logico) e NOT (negazione o complementazione).

Si descriveranno, inoltre, le porte logiche derivate NOR (OR seguito da un NOT), NAND (AND seguito da un NOT), XOR (noto come OR esclusivo o circuito di anticoincidenza), XNOR (noto come NOR esclusivo o circuito di coincidenza).

Ogni porta logica ha una o più variabili di ingresso ed una sola variabile di uscita. Le variabili di ingresso e di uscita sono di tipo digitale per cui è possibile inserire in una tabella tutte le possibili combinazioni che si possono verificare tra le variabili di ingresso. L'uscita assume il valore 0 oppure il valore 1 in corrispondenza di ciascuna combinazione delle variabile di ingresso in funzione della definizione assegnata.

1. Somma logica OR

Si effettua su due o più variabili, l'uscita assume lo stato logico 1 se almeno una variabile di ingresso è allo stato logico 1.

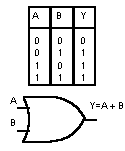
Nel caso di due variabili di ingresso A e B, detta Y la variabile di uscita, si scrive: Y=A+B e si legge A or B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta OR a due ingressi. Nella colonna Y si sono posti i valori assunti dall'uscita Y che soddisfa la definizione della porta OR.

2. Prodotto logico AND

Si effettua su due o più variabili, l'uscita assume lo stato logico 1 solo se tutte variabile di ingresso sono allo stato logico 1.

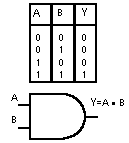
Nel caso di due variabili di ingresso A e B, detta Y la variabile di uscita, si scrive: Y=A·B e si legge A and B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta AND a due ingressi. Nella colonna Y si sono posti i valori assunti dall'uscita Y che soddisfa la definizione della porta AND.

3. Negazione

Si effettua su una sola variabile. L'uscita assume il valore logico opposto a quello applicato in ingresso.

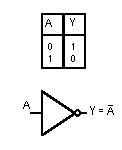
Detta A la variabile di ingresso la negazione si scrive: Y = A e si legge A negato oppure A complementato.

Nella seguente figura si mostra la tabella della verità con le due possibili combinazioni di A ed il simbolo logico relativo ad una porta NOT. Nella colonna Y si sono posti i valori assunti dall'uscita Y che soddisfa la definizione della porta NOT.

4. Somma logica negata NOR

Si effettua su due o più variabili, l'uscita assume lo stato logico 0 se almeno una variabile di ingresso è allo stato logico 1. In tutti gli altri casi Y=1.

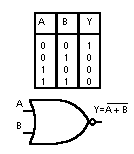
Per due variabili di ingresso A e B:   Y= A+B e si legge A nor B.

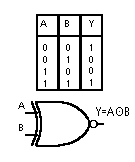
Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta NOR a due ingressi. Nella colonna Y si sono posti i valori assunti dall'uscita Y che soddisfa la definizione della porta NOR.

5. Prodotto logico negato NAND

Si effettua su due o più variabili, l'uscita assume lo stato logico 0 se tutte le variabili di ingresso sono allo stato logico 1. In tutti gli altri casi Y=1.

Per due variabili di ingresso A e B: Y = A·B e si legge A nand B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta NAND a due ingressi. Nella colonna Y si sono posti i valori assunti dall'uscita Y che soddisfa la definizione della porta NAND.

6. OR esclusivo XOR

A differenza delle precedenti porte logiche, l'XOR opera su due soli ingressi. L'uscita vale 1 se gli ingressi assumono valore diverso, vale 0 se gli ingressi sono tra loro uguali. La funzione logica si scrive: e si legge A or esclusivo B oppure A diverso da B.

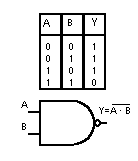
Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta XOR. Nella colonna Y si sono posti i valori assunti dall'uscita Y che soddisfa la definizione della porta XOR.

7. NOR esclusivo XNOR

Anche la porta XNOR opera su due soli ingressi. L'uscita vale 1 se gli ingressi assumono valore uguale, vale 0 se gli ingressi sono tra loro diversi. La funzione logica si scrive: e si legge A nor esclusivo B oppure A coincidente con B.

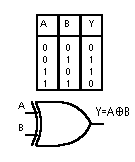
Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta XNOR. Nella colonna Y si sono posti i valori assunti dall'uscita Y che soddisfa la definizione della porta XNOR.

Le porte logiche

(parte seconda)

Le porte logiche esaminate nel numero scorso si dividono in porte logiche fondamentali e porte logiche derivate.

Quelle fondamentali sono: somma logica OR, prodotto logico AND e negazione NOT.

Le porte logiche derivate sono: la somma logica negata NOR, il prodotto logico negato NAND, l'OR esclusivo XOR o circuito di anticoincidenza e il NOR esclusivo XNOR o circuito di coincidenza.

Le porte logiche fondamentali costituiscono i mattoni dell'elettronica digitale.

Con esse è possibile realizzare qualsiasi circuito digitale dal più semplice al più complesso.

È, inoltre, possibile verificare che anche con le sole porte NOR o con le sole porte NAND è possibile realizzare qualsiasi circuito digitale. È sufficiente, infatti, verificare che con le sole porte NAND, ad esempio, si può realizzare il NOT, l'OR e l'AND.

Infatti collegando tra loro gli ingressi A e B della porta NAND come in figura 1 si ottiene il NOT:

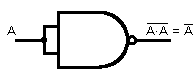
Fig.1 - NOT realizzato con una porta NAND.

Per ottenere l'AND è sufficiente far seguire la porta NAND da un NOT realizzato come in figura 1.

Per ottenere l'OR, infine è sufficiente far precedere ciascun ingresso del NAND da un NOT come in fig.2. Infatti, per il noto teorema di De Morgan, la somma logica è il complemento del prodotto dei complementi.

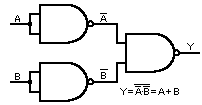
Fig.2 - OR realizzato con porte NAND.

Progettazione di un semplice circuito digitale combinatorio.

Si vuole realizzare un circuito digitale combinatorio con tre ingressi A B C ed una uscita Y.

L'uscita deve valere 1 se almeno due ingressi sono uguali ad 1. Se, invece, vale 1 un solo ingresso o nessuno di essi l'uscita Y deve valere 0 (problema della maggioranza).

Risoluzione

Compiliamo una tabella, nota come tabella della verità, in cui in ciascuna riga applichiamo le possibili combinazioni binarie tra gli ingressi A B C. Tali combinazioni sono: 2³=8.

In corrispondenza di ciascuna di esse sarà possibile, grazie alla formulazione del problema, assegnare all'uscita Y il valore 0 o il valore 1.

Dalla tabella osserviamo che l'uscita Y assume il valore 1 in corrispondenza delle combinazioni ABC pari a 011, 101, 110 e 111.

Nell'ultima combinazioni tutti gli ingressi sono a 1 per cui, a maggior ragione, risulta Y=1.

Per le altre combinazioni l'uscita Y vale 0 come richiesto dal problema.

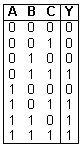
Come si realizza il circuito? Sarà, innanzitutto, necessario ricavare l'espressione algebrica dalla tabella della verità.

Il procedimento è il seguente: si considerano le combinazioni delle variabili di ingresso che rendono l'uscita Y uguale a 1. La combinazione di ingresso da considerare conterrà il prodotto tra A B C e ciascuna variabile sarà considerata in forma naturale o in forma negata a seconda se assume il valore 0 o 1. La prima combinazione che rende l'uscita uguale a 1 è: ABC=011, cioè A=0, B=1 e C=1. Allora A dovrà essere considerata in forma negata (complementata), mentre B e C in forma naturale (cioè senza negazione). I quattro termini che rendono la variabile di uscita Y uguale a 1 devono, poi, essere sommati (somma logica !!) tra di loro.

In definitiva si ottiene:

Questa espressione si può semplificare algebricamente applicando le regole dell'algebra di Boole che solo parzialmente coincidono con quelle dell'algebra ordinaria.

In particolare, per la semplificazione che si intende effettuare, si applica la regola che aggiungendo quante volte si vuole un termine già esistente in una espressione, il valore dell'espressione non cambia. L'altra regola è che la somma logica tra una variabile e la stessa variabile negata vale 1.

Nel nostro caso aggiungiamo, nella espressione della funzione Y, il termine ABC per altre due volte. In tal caso il primo termine ha BC in comune con ABC, il secondo ha AC in comune con l'altro ABC aggiunto ed infine il terzo termine ha AB in comune con l'ultimo ABC aggiunto.

Attraverso la messa in evidenza si ottiene:

A + A=1 e così pure B + B = 1 e C + C = 1 , l'espressione si riduce a:

L'espressione così minimizzata è una somma di prodotti. Il circuito logico da realizzare sarà costituito da tre porte AND a due ingressi e da una porta OR finale a tre ingressi. In fig.3 si mostra il circuito risolutivo.

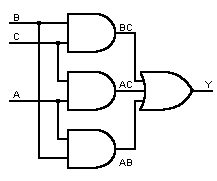
Fig.3 - Circuito risolutivo.

Per verificarne il funzionamento è sufficiente attribuire alle variabili di ingresso A B C ciascuna delle otto combinazioni mostrate nella precedente tabella ed eseguendo la somma logica tra i tre termini prodotto BC, AC e AB.

I multiplexer a cura del prof. Giuseppe Spalierno docente di Elettronica e Sistemi presso l'I.T.I. "Modesto PANETTI" di BARI

Sono dispositivi in grado di trasferire 131b16b in uscita una sola di 2ⁿ possibili linee di ingresso. La selezione della linea di ingresso da traferire in uscita dipende da n linee di controllo.
Il multiplexer è assimilabile ad un commutatore a posizioni multiple; la posizione dipende dai bit di controllo.
Si mostra in fig.1 la tabella della verità e il simbolo equivalente di un multiplexer a 4 ingressi A B C D e  2 linee di controllo (o selezione) S1 e S0.
 

Ingressi di selezione  uscita S1 S0 Y A  B C D

  Fig.1 Tabella della verità e simbolo equivalente di un multiplexer a 4 ingressi.  

La funzione di uscita Y del multiplexer vale:

Y = S1·S0·A + S1·S0·B + S1·S0·C + S1·S0·D

Nel caso di un multiplexer a due ingressi P1 e P2 ed un ingresso di selezione S, l'uscita Y assume la seguente espressione, trasformata applicando il teorema di De Morgan:

Il circuito logico risolutivo, realizzato a porte NAND, è mostrato in fig.2.

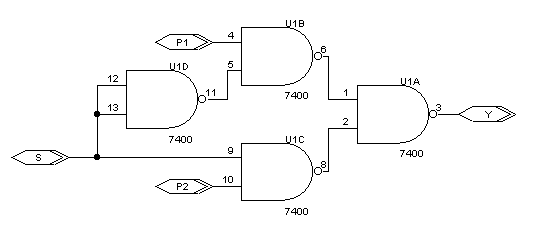
Fig.2 Multiplexer a due ingressi realizzato nella logica a porte NAND.

In commercio sono disponibili circuiti integrati che contengono multiplexer a 2 ingressi, 4 ingressi, 8 ingressi e 16 ingressi. Il multiplexer 74157 contiene 4 MUX a 2 ingressi, il 74153 contiene 2 MUX a 4 ingressi, il 74151 contiene 1 MUX a 8 ingressi.  Si riporta, in fig.3, la piedinatura dei citati multiplexer.

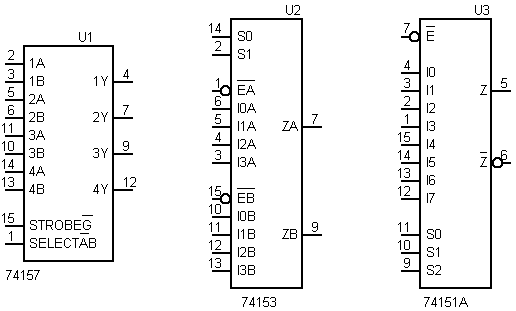
Fig.3 Piedinatura di 3 multiplexer della famiglia logica TTL.

Cenni sulle famiglie logiche TTL e CMOS

1. Generalità

I dispositivi digitali vengono suddivisi in famiglie logiche ciascuna delle quali differisce dalle altre per la tecnologia utilizzata e per il circuito di base con cui si realizzano le porte logiche.

Nell'ambito della stessa famiglia logica vi sono diverse serie atte a migliorare alcune caratteristiche elettriche rispetto ad altre.

Le famiglie logiche più utilizzate sono la TTL (Transistor -Transistor Logic) e la CMOS (Complementary MOS).

La prima prende il nome di TTL per la presenza di transistor sia nello stadio di ingresso che di uscita.

La seconda si chiama CMOS perché fa uso di MOSFET (Transistor ad Effetto di Campo MOS, Metallo Ossido Semiconduttore).

2. Famiglia logica TTL

Tutti i circuiti integrati della famiglia logica TTL sono alimentati con Vcc=+5V, sono caratterizzati da un numero di serie che ha, come cifre iniziali, 74 (serie commerciale che funziona tra 0 e 70°C) o 54 (serie militare che funziona tra -55 e +125°C).

I livelli di tensione da applicare in ingresso sono:

• V_IL compreso tra 0 e +0.8V per il riconoscimento del livello logico basso;
• V_IH compreso tra +2V e +5V per il riconoscimento del livello logico alto.

I valori di tensione compresi tra 0.8V e 2V individuano una zona di indeterminazione che è bene non utilizzare.

I livelli di tensione che si ottengono in uscita sono:

• V_OL compreso tra 0 e 0.4V con corrente di sink I_OL<16mA
• V_OH compreso tra 2.4V e circa 4V con corrente di source I_OH< 400µA.

 

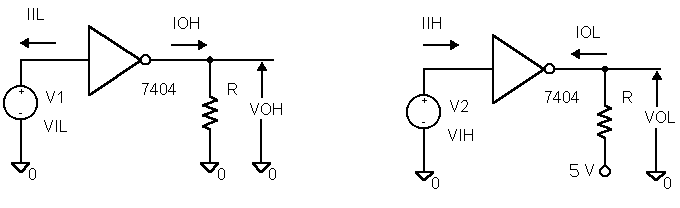
Fig.1 Disposizione di un NOT TTL per la valutazione della tensione e corrente di ingresso e di uscita.

In fig.1 si mostra una porta NOT pilotata con un generatore di tensione che fornisce in ingresso una tensione V₁ = V_IL e V₂ = V_IH e i relativi versi delle correnti I_IL, I_IH, I_OH, I_OL. Sono indicate, inoltre, le tensioni di uscita V_OH e V_OL.

Si riportano nella tabella 1 le caratteristiche più importanti delle diverse serie della famiglia logica TTL ricordando che:

L è la serie a basso consumo (Low power), ormai obsoleta;

S è la serie che impiega i veloci transistor Schottky;

LS è la serie che riunisce le due precedenti caratteristiche (Low power Schottky);

AS è la serie S tecnologicamente Avanzata;

ALS è la serie LS tecnologicamente Avanzata.

Tabella 1

3. Famiglia logica CMOS

I circuiti integrati appartenenti alla famiglia logica CMOS (Complementary MOS) utilizzano al loro interno transistor MOSFET  a canale N ed a canale P, quindi di tipo complementare.
La caratteristica fondamentale di un componente CMOS è la ridottissima potenza dissipata in condizioni statiche: circa 10nW per porta logica e un ampio intervallo di valori di tensione di alimentazione: da 3V a 15V.
In commercio sono disponibili diverse serie della famiglia logica CMOS che di seguito si elencano:

• CD4000 ormai obsoleta;
• 74C compatibile, nella piedinatura, ai corrispondenti integrati della famiglia logica TTL;
• 74HC e 74HCT come la precedente ma con tempi di propagazione ridotti (intorno a 10-15ns) e valori di alimentazione da 2V a 6V (HC) e 5V (HCT)
• 74AHC simile alla famiglia HC ma con prestazioni "Avanzate".

L'uso dei dispositivi CMOS impone l'osservanza di alcune regole:

• La tensione applicata in ingresso deve essere compresa tra 0 e Vcc;
• I piedini di ingresso non devono essere mai inutilizzati: essi vanno collegati al livello logico alto o basso;
• Il terminale di uscita può essere collegato direttamente a massa o all'alimentazione senza il pericolo di avarie poiché lo stadio di uscita è di tipo resistivo, cioé si può assimilare ad un generatore di tensione avente in serie una resistenza;
• La tensione di soglia di commutazione è circa la metà della tensione di alimentazione applicata.

I livelli di tensione da applicare in ingresso sono:

• V_IL compreso tra 0 e +Vcc/3 per il riconoscimento del livello logico basso;
• V_IH compreso tra +2Vcc/3  e +Vcc per il riconoscimento del livello logico alto.

I valori di tensione compresi tra Vcc/3 e 2Vcc/3 individuano una zona di indeterminazione che è bene non utilizzare.

I livelli di tensione che si ottengono in uscita, in assenza di carico applicato, sono:

• V_OL = 0 ;
• V_OH = Vcc.

Le correnti di ingresso I_IL e I_IH sono praticamente nulle perchè l'ingresso dei transistor MOSFET presenta resistenza infinita.
Le correnti di uscita I_OL e I_OH dipendono dalla particolare serie CMOS utilizzata e comunque generalmente non superano il valore di alcuni milliampere.

4. Le moderne famiglie logiche

In questi ultimi anni si sono rese disponibili sul mercato numerose altre famiglie logiche molto più efficienti della classica TTL e della classica CMOS serie 4000 e serie 74C.

Le tecnologie utilizzate per queste nuove famiglie logiche sono ancora di tipo CMOS e di tipo BICMOS (transistor bipolari e CMOS) aventi, come caratteristiche particolarmente interessanti, un ridottissimo autoconsumo ed elevata frequenza di funzionamento. In particolare, si citano le famiglie logiche a bassa tensione di alimentazione (famiglie logiche Low Voltage), tipicamente a +3.3V, con elevati valori di corrente di carico e compatibili con i livelli logici delle famiglie alimentate a +5V.

In fig.2 si mostra un grafico che illustra la posizione occupata, dalle varie famiglie logiche, nel tipico ciclo di vita in cui si evidenzia una fase di introduzione, una di crescita, una di maturità, una di declino e l'ultima di obsolescenza.

La figura è tratta dalla documentazione fornita dalla Texas Instruments.

Dalla figura si nota che le nuove famiglie logiche hanno una tecnologia di tipo CMOS o BICMOS e sono a bassa tensione. Le sigle riportate hanno il seguente significato:

LV - Low Voltage CMOS.

ALV - Advanced Low Voltage CMOS

ABT - Advanced BICMOS Technology

Le cause che hanno spinto i costruttori a realizzare famiglie logiche alimentate con bassi valori di tensione sono sostanzialmente riassunte nei seguenti punti:

• La riduzione orizzontale e verticale della geometria del wafer dei moderni dispositivi integrati a semiconduttori richiede una più bassa tensione di alimentazione pena la possibilità di breakdown dell'ossido del MOS. Ciò potrebbe rendere il dispositivo inutilizzabile.

• I costruttori di apparecchi elettronici alimentati a pile chiedono componenti elettronici a bassa dissipazione di potenza. La potenza consumata, come è noto, dipende dai carichi elevati, è direttamente proporzionale alla frequenza di lavoro, ed è proporzionale al quadrato della tensione di alimentazione.

• Il ridotto consumo di potenza riscalda di meno i componenti e ciò consente di evitare l'uso di ingombranti e costosi dissipatori di calore e permette la realizzazione di dispositivi a maggior grado di integrazione.

 

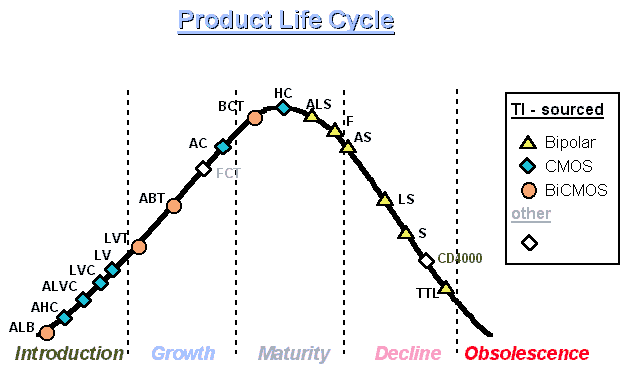
Fig.2 Stato attuale delle famiglie logiche nel ciclo di vita.

Le caratteristiche elettriche delle famiglie logiche a bassa tensione di alimentazione sono sostanzialmente simili a quelle delle corrispondenti famiglie logiche alimentate a 5V. Se ne riportano alcune in tabella 2.

Tabella 2

In fig.3 si riportano i livelli di tensione di ingresso, uscita e della soglia di commutazione delle famiglie logiche a bassa tensione e delle famiglie logiche a 5V TTL e CMOS.

 

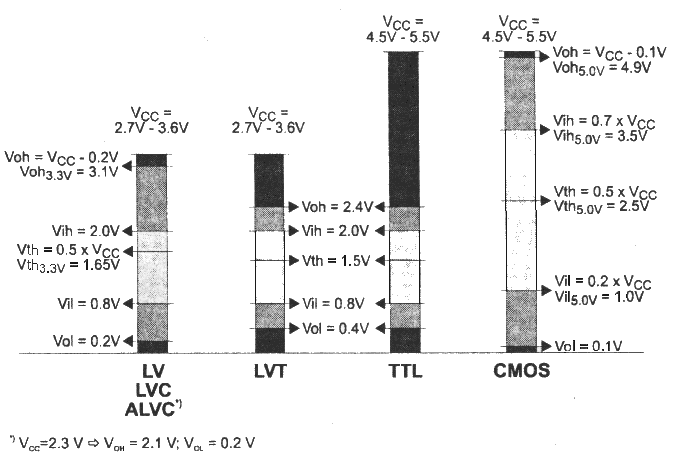
Fig.3 Confronto dei livelli delle famiglie logiche a bassa tensione con quelli delle famiglie TTL e CMOS a 5V.

Tralasciando la descrizione delle altre caratteristiche elettriche e degli schemi interni, concludiamo questa nota riportando, nella successiva fig.4, un grafico che individua la posizione delle varie famiglie logiche in un piano avente per assi la corrente di alimentazione e il tempo di ritardo di propagazione. Una buona famiglia logica deve potersi collocare nelle immediate vicinanze dell'origine degli assi, posizione occupata dalle tecnologie ACL, BCT e ABT.

Si consideri, infine, che queste nuove famiglie logiche non contengono tutti i circuiti logici come la TTL; alcune sono specializzate come bus driver e quindi annoverano integrati con array di buffer invertenti o non invertenti con uscite tristate o array di flip-flop D anch'essi con uscita tristate.

 

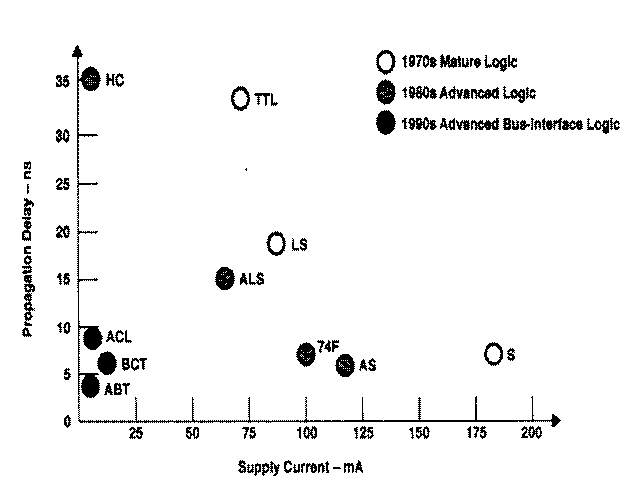
Fig.4

5. Famiglia logica AHC

La famiglia logica CMOS ad alta velocità in tecnologia avanzata (AHC) è una delle ultime apparse sul mercato ed unisce alla bassa potenza dissipata, tipico della CMOS, una elevata velocità di funzionamento.
La famiglia logica AHC consiste di porte logiche elementari, di integrati della media scala e di dispositivi ottali (driver e flip-flop per collegamenti a bus a 8 bit).
La famiglia logica AHC è quasi tre volte più veloce della HC poichè il tipico tempo di ritardo di propagazione è di circa 5.2ns, presenta bassi valori di rumore, non presenta problemi di overshoot e di undershoot, dissipa una potenza  inferiore rispetto alla HC, presenta una capacità di carico di 8mA per Vcc=5V e 4mA per Vcc=3.3V.
Si mostra nella tabella 3 i valori del tempo di ritardo di propagazione di alcuni tipici dispositivi della famiglia logica AHC comfrontati con quelli della famiglia logica HC.

Tabella 3

La potenza dissipata da un dispositivo CMOS dipende da tre fattori:

potenza dissipata a riposo P_q (quiescient power)

potenza dissitapa in transitorio P_t (transient power)

potenza dissipata capacitiva P_c (capacitive power)

La potenza dissipata a riposo P_q dipende dalla tensione di alimentazione V_cc e dalla corrente I_cc che scorre a riposo nel dispositivo. In formule si ha:

P_q = V_cc x I_cc

Poichè I_cc è molto bassa, P_q è spesso trascurabile.

La potenza dissipata in transitorio P_t dipende dalla corrente che fluisce nei transistor interni quando essi commutano da un livello logico all'altro. Durante questo tempo i due transistor dello stadio finale sono parzialmente in conduzione e ciò produce un piccolo spike di corrente che viene ripetuto, in un secondo, un numero di volte pari alla frequenza  f_i di input. L'intensità di corrente dipende dalla tensione di alimentazione V_cc e la potenza dissipata, quindi, dal quadrato della corrente. La durata di ciascuno di questi spikes dipende anche dalla rapidità di commutazione dei transistor e quindi dalla capacità parassita C_pd (power dissipation capacitance). In formule si ha:

P_t = C_pd x V_cc² x f_i

La potenza dissipata capacitiva P_c dipende dalla carica e dalla scarica di capacità esterne C_L e dipende dalla frequenza di commutazione f_o secondo la formula:

P_c = C_L x V_cc² x f_o

FLIP -FLOP

a cura del prof. Giuseppe Spalierno docente di Elettronica e Sistemi
presso l'I.T.I. "Modesto PANETTI" di BARI
ultima versione: dicembre 2003

1. Premessa
I flip flop sono circuiti digitali sequenziali che hanno il compito di memorizzare un bit.
Un circuito digitale si dice sequenziale se l'uscita dipende dagli ingressi applicati e dallo stato precedente della stessa uscita.
Un circuito sequenziale, pertanto, deve ricordare il suo stato precedente e quindi deve possedere uno o più elementi di memoria.
I circuiti digitali si dividono in due fondamentali categorie:

1. combinatori (il valore dell'uscita dipende solo dal valore dei bit applicati in ingresso);
2. sequenziali (il valore dell'uscita dipende anche dal suo stato precedente).

I flip-flop sono noti, anche, come multivibratori bistabili perché ciascuno degli stati logici 0 e 1 può essere reso stabile nel tempo.
I multivibratori si dividono in:

1. astabili (nessuno stato stabile - ad esempio i generatori di onde quadre);
2. monostabili (un solo stato stabile - ad esempio i temporizzatori);
3. bistabili (due possibili stati stabili - ad esempio una cella di memoria).

2. Flip-flop SR (Set-Reset)
Il più semplice dispositivo di memoria è il flip-flop Set-Reset. Esso possiede due ingressi denominati Set e Reset ed una uscita indicata con Q.
I circuiti digitali che realizzano il flip flop sono dotati, spesso, anche dell'uscita Q .
Occorre precisare, inoltre, che in un dispositivo di memoria, l'uscita dipende non solo dalla particolare combinazione assunta dalle variabili di ingresso ma anche dallo stato precedente assunto dall'uscita Q. Tale stato precedente verrà indicato con Qo.

2.1. Flip-flop SR con porte NOR
Alla luce di quanto detto si mostra in figura 1 il simbolo logico, la tabella della verità e la soluzione circuitale a porte logiche NOR di un flip-flop S-R.

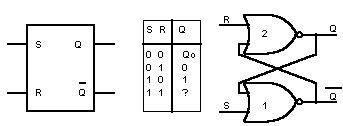
Fig.1 - Flip-flop S-R. Simbolo, tabella della verità e soluzione circuitale con porte NOR. 

Combinazione SR=00.
Essa è nota come combinazione di riposo poiché l'uscita conserva lo stato precedente (Q=Qo).

Combinazione SR=01.
Ponendo R=1, l'uscita Q si porta a 0 indipendentemente dallo stato precedente.

Combinazione SR=10.
Ponendo S=1, l'uscita Q si porta a 1 indipendentemente dallo stato precedente.

Combinazione SR=11.
Tale combinazione va evitata poiché da un punto di vista logico è una incongruenza: infatti non ha senso comandare il flip-flop per memorizzare lo 0 (R=1) oppure l'1 (S=1). 

Tale flip-flop viene spesso utilizzato per funzionare nel modo seguente.
Se si vuole memorizzare 1 si pone: S=1 e R=0. Successivamente si torna nello stato di riposo: S=0 e R=0. In tal caso l'uscita conserva lo stato precedente: Q=Qo=1.
Se si vuole memorizzare 0 si pone: S=0 e R=1. Successivamente si torna nello stato di riposo: S=0 e R=0. In tal caso l'uscita conserva lo stato precedente: Q=Qo=0.

Verifichiamo, infine, che il circuito realizzato con le porte NOR in figura 1 si comporta da flip-flop S-R.
Dobbiamo ricordare, a tal fine, la tabella della verità della porta NOR (somma logica negata).

Ponendo S=0 e R=1 si deve verificare che Q=0. Infatti l'uscita Q della porta 2 va a 0 poiché l'ingresso R=1.
La porta 1 risulta pilotata con gli ingressi uguali a 0 per cui la sua uscita va a 1. Si noti che le due uscite sono complementari tra loro.
Torniamo nella combinazione di riposo portando R=0 e lasciando S=0.
Poiché l'uscita Q precedentemente era stata portata a 0 (Qo=0), l'uscita della porta 1 rimane a 1 e di conseguenza l'uscita della porta 2 rimane a 0 (Q=0).

Poniamo, ora: S=1 e R=0. L'uscita della porta 1 va a 0 e di conseguenza, poiché R=0, l'uscita della porta 2 si porta a 1: Q=1.
Torniamo nella combinazione di riposo portando S=0 e lasciando R=0.
Poiché l'uscita Q precedentemente era stata portata a 1 (Qo=1), l'uscita della porta 1 rimane a 0 e di conseguenza l'uscita della porta 2 rimane a 1 (Q=1).

Se, infine applichiamo S=1 e R=1, le uscite di entrambe le porte andranno a 0. Conseguenze: le due uscite, in questo caso, non sono più l'una il complemento dell'altra, ed inoltre portando contemporaneamente S ed R a 0 entrambe le uscite si porteranno ad 1 e poi a 0 e così via. In realtà, a causa dei diversi tempi di ritardo di propagazione del segnale elettrico in ciascuna porta, uno dei due NOR propagherà l'1 in uscita prima dell'altra porta. In conclusione diventa aleatorio il valore dell'uscita Q che, pertanto, potrà trovarsi o a 0 o a 1. Anche per questo motivo è bene evitare l'applicazione dell'ultima combinazione della tabella della verità: S=1 e R=1. 

2.2. Flip-flop a porte NAND
Si riporta in fig.2 lo schema logico del flip-flop realizzato a porte NAND.
Qui gli ingressi sono indicati con le lettere A e B che, sostanzialmente, si comportano come gli ingressi S ed R del precedente flip-flop a porte NOR con la differenza che gli ingressi sono attivi in logica negativa. In altre parole i flip-flop di fig.1 e di fig.2 coincidono nella funzione logica purché si ponga: 

A = S ,   B = R

Ponendo AB=10 si realizza la funzione di reset per cui l'uscita Q si porta a 0.
Ponendo AB=01 si realizza la funzione di set per cui l'uscita Q si porta a 1.
Ponendo AB=11 si realizza la funzione di memoria per cui l'uscita conserva il precedente valore memorizzato.
AB=00 è la combinazione da evitare sia per incongruenza logica sia perché porterebbe entrambe le uscite al valore 1 e quindi non sarebbero una il complemento dell'altra.

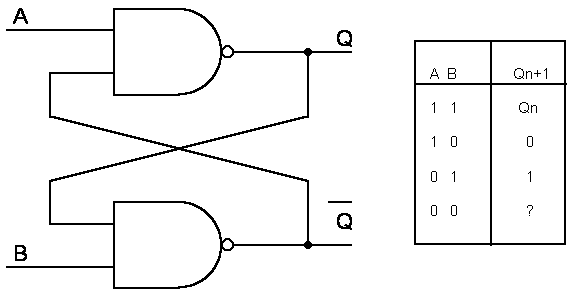
Fig.2 - Flip-flop S-R con porte NAND. Soluzione circuitale e tabella della verità . 

3. Flip-flop sincronizzati

Spesso l'eventuale cambiamento di stato di un flip-flop non si fa coincidere con l'istante in cui si modificano i valori dei bit di ingresso ma con l'istante in cui un ulteriore ingresso, detto ingresso di sincronismo o ingresso di clock e denominato con la sigla CK, va da 1 a 0 oppure da 0 a 1.
Un flip-flop che funziona col clock prende il nome di flip-flop sincronizzato.
I flip-flop esaminati nelle figure 1e 2, invece, essendo privi di ingresso di clock, sono denominati flip-flop Set Reset asincroni.

Il flip-flop si dice attivo sul livello quando il clock è caratterizzato da un livello logico (0 o 1) applicato all'omonimo ingresso.
Il flip-flop si dice attivo su fronti (edge triggered) quando l'eventuale modifica dello stato di uscita dipende dal fronte positivo o di salita (PET = Positive Edge Triggered) o dal fronte negativo o di discesa (NET = Negative Edge Triggered).
Sui dice, anche, che l'uscita si aggiorna nel:

PET quando il clock passa da 0 a 1;

NET quando il clock passa da 1 a 0.

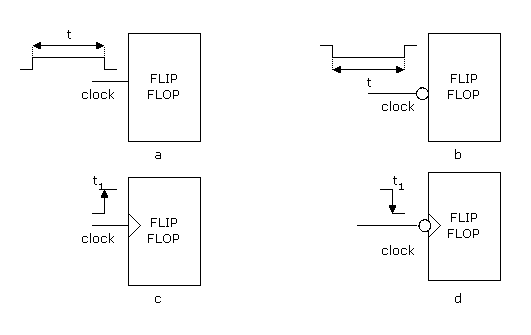
Fig.3 - Flip-flop sensibili ai livelli ed alle transizioni.
Il flip-flop "a" è sensibile al livello logico 1 e funziona nell'intervallo di tempo t.
Il flip-flop "b" è sensibile al livello logico 0 durante il tempo t.
Il flip-flop "c" è di tipo PET e funziona solo nell'istante t_1.
Il flip-flop "d", infine, è di tipo NET e funziona solo nell'istante t₁.

3.1. Flip-flop S-R sincronizzato
In fig.4 si mostra lo schema logico del flip-flop Set Reset sincronizzato. Esso è costituito da due porte logiche NAND, dette porte pilota, e da altre due porte NAND che realizzano il flip-flop S R vero e proprio del tipo mostrato nella precedente fig.2.

Se il clock CK è al livello logico 1 le porte pilota si comportano da NOT e quindi gli ingressi S ed R sono effettivamente coincidenti con gli omonimi ingressi del generico flip-flop Set Reset.

Se, invece, il clock CK è al livello logico basso, le uscite delle due porte pilota sono al livello logico 1 indipendentemente dai valori applicati agli ingressi S e R. Per tale combinazione la "latch" a porte NAND conserva lo stato precedente e quindi il flip flop è insensibile ai comandi esterni applicati.

Nella tabella della verità si riporta l'uscita futura Q_{n+1 in funzione del clock, degli ingressi S ed R e dallo stato presente Qn.}

X rappresenta indifferentemente sia lo stato logico 0 che lo stato logico 1.

CK S R Qn Qn+1 X X X X da evitare

Fig.4. - Flip-flop SR sincronizzato con porte NAND.
U1A e U1B costituiscono le porte pilota.
Le porte U1C e U1D rappresentano il flip-flop vero e proprio.
Con Qbar si indica l'uscita Q (Q barrata).

4. Flip-flop JK

Il flip-flop JK è un dispositivo a due entrate denominate J e K che operano in modo analogo alle entrate S ed R di un flip-flip Set Reset con la differenza che se : J=1 e K=1 l'uscita commuta, cioè se lo stato presente è 0, lo stato futuro è 1 e viceversa.
Per evitare commutazioni multiple, nel caso si lasci a lungo la combinazione J=1 e K=1, tale flip-flop deve essere necessariamente sincronizzato.

J K Qn Qn+1

Fig.5. - Flip-flop JK e tabelle della verità. A destra si mostra la tabella della verità che prescinde dalla presenza del clock e che mostra l'uscita futura in presenza degli ingressi esterni J e K e dallo stato presente Q_n.

In fig.5 si mostrano due flip-flop JK sincronizzati. Il primo adegua le uscite quando al clock si applica un segnale digitale che passa da 0 a 1 (transizione positiva indicata con una freccia verso l'alto nella tabella della verità). Il secondo adegua le uscite quando al clock si applica un segnale digitale che passa da 1 a 0 (transizione negativa indicata con una freccia verso il basso nella tabella della verità).

Il primo flip flop JK si dice di tipo PET (Positive Edge Triggered), il secondo, invece, si dice di tipo NET (Negative Edge Triggered).

I flip-flop JK si realizzano con una soluzione circuitale costituita da porte logiche secondo uno schema interno più complesso rispetto a quello visto per il flip-flop SR realizzato a porte NOR e a porte NAND.

Si mostrano, in fig.6, i simboli logici e le tabelle della verità di due diversi flip-flop JK, il primo di tipo PET ed il secondo di tipo NET, con ingressi asincroni di preset (PRE) e di cleear (CLR).

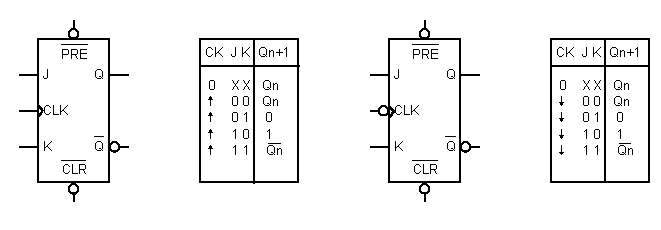
Fig.6 - Simbolo del flip-flop JK PET e relativa tabella della verità ( a sinistra);
simbolo del flip-flop JK NET e relativa tabella della verità ( a destra).
Si noti il simbolo del clock nei due casi.
La maggior parte dei flip-flop integrati presentano, inoltre, ingressi asincroni di preassegnazione a 1 (PRE) e/o di azzeramento (CLR clear).
Quelli indicati in figura sono attivi bassi: se, ad esempio, si applica un livello logico basso sulla linea PRE, il flip-flop memorizza 1 indipendentemente dal clock; se, invece, si applica un livello logico basso sulla linea CLR, il flip-flop memorizza 0 indipendentemente dal clock.

5. Flip-flop D

Presenta un solo ingresso denominato D. Spesso è di tipo sincronizzato e funziona nel seguente modo: quando è attivo l'ingresso di clock l'uscita assume lo stesso valore applicato all'ingresso D. In assenza di comando di clock l'uscita conserva lo stato precedente indipendentemente dal valore applicato all'ingresso D.
In fig.7 si mostra il simbolo logico e la tabella della verità del flip -flop D.
Il flip-flop D rappresenta l'elemento fondamentale delle memorie centrali degli elaboratori ( almeno a livello concettuale).

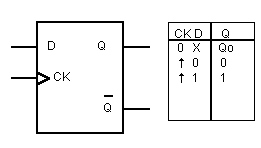
Fig.7 - Flip-flop D e relativa tabella della verità. 

6. Flip-flop T
E' un flip-flop avente una sola entrata denominata T e le solite due uscite: Q e la sua complementata Q.
L'uscita Q conserva lo stato precedente se T=0 e commuta se T=1 quando si applica il segnale di clock.
I flip-flop T, al contrario dei JK, D e SR, non sono disponibili commercialmente in forma  integrata poiché si possono ottenere direttamente dai flip-flop JK semplicemente collegando tra loro gli ingressi J e K.
E'  utilizzato come dispositivo divisore di frequenza di clock per due e nei contatori digitali.
Si mostra in fig.8 il collegamento di un flip-flop NET di tipo JK per ottenere un flip-flop di tipo T e la relativa tabella della verità.

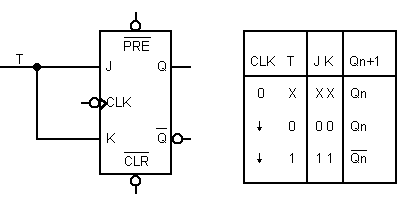
Fig.8 -   Simbolo del flip-flop T e relativa tabella della verità.
Dalla tabella si nota che solo quando il clock passa dal livello logico alto al livello logico basso si ha:
 Q_n+1=Q_n se T=0 e Q_n+1=Q_n  se T=1.

7. Diagramma degli stati
Le possibili modalità di funzionamento di un flip-flop e, più in generale, di qualsiasi circuito digitale con uno o più flip-flop, possono essere descritte in diverse modalità: tabella della verità, equazione caratteristica, tabella delle transizioni, diagramma degli stati. Le varie modalità sono tra loro perfettamente equivalenti per cui da ciascuna rappresentazione è possibile ricavare qualsiasi altra.
In questa sede si vuole ricavare il diagramma degli stati del flip-flop J-K.
Il procedimento per ricavare il diagramma degli stati degli altri flip-flop è del tutto equivalente.

Intanto diciamo subito che per diagramma degli stati si intende una rappresentazione grafica dei vari stati o valori logici che il sistema digitale sequenziale può assumere. Nel caso del singolo flip-flop, che possiede una sola uscita Q, i possibili stati sono due: 0 e 1.
I due valori si inseriscono in altrettanti cerchietti ognuno dei quali rappresenta il punto di arrivo o il punto di partenza di un arco orientato che rappresenta la transizione dello stato interno del circuito.  L'arco orientato è condizionato  dagli ingressi esterni che, per il flip-flop JK, sono gli ingressi J e K.

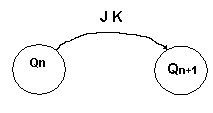
Fig.9. - L'arco orientato individua il passaggio di stato condizionato dagli ingressi J e K

   In fig.10 si mostra il diagramma degli stati del flip-flop JK. Per poterlo costruire si è tenuta presente la tabella della verità rappresentata nella parte destra della fig.5. Per ogni combinazione si tiene conto dei valori degli ingressi J e K e di quelli dello stato presente Q_n e futuro Q_n+1.

Per la prima combinazione, ad esempio, si ha: J=K=0 e Q_n=Q_n+1=0.
Si deve disegnare, pertanto, un arco orientato che parte dallo stato 0 (stato presente Q_n) e termina nello stesso stato 0 (stato futuro Q_n+1).
Si procede con lo stesso ragionamento per le altre combinazioni.
Per l'ultima combinazione si ha: J=K=1, Q_n=1 e Q_n+1=0.
L'arco orientato parte dallo stato 1 e termina nello stato 0. Sull'arco orientato si scrivono i due valori degli ingressi J e K: 11.

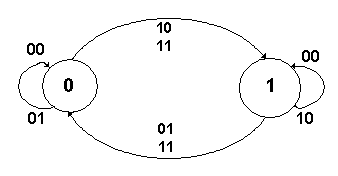
Fig.10. - Diagramma degli stati del flip-flop JK.

8. Tabella delle transizioni
Si indica col nome di tabella delle transizioni la mappa di Karnaugh in cui si inseriscono i valori che assume lo stato futuro Q_n+1 dell'uscita  in funzione degli ingressi e dello stato presente Q_n. Nel caso del flip-flop JK gli ingressi da considerare sono J e K.

Si mostra, in fig.11, la tabella delle transizioni del flip-flop JK. Essa si ricava dalla tabella della verità di fig.5 o, indifferentemente, dal diagramma degli stati della precedente fig.10.

JK Qn

Fig.11. - Tabella delle transizioni per un flip-flop JK. Le celle in cui compare un bit coincidente col valore di Qn (celle con sfondo giallo) rappresentano uno stato stabile poiché un impulso di clock non modifica lo stato di uscita Q. Sono stabili i due stati della prima colonna (JK=00), lo stato superiore della seconda colonna e lo stato inferiore della quarta colonna. Gli altri sono stati instabili.

La funzione minimizzata che si ricava dalla precedente tabella delle transizioni prende il nome di equazione caratteristica e vale:

Q_n+1 = J·Q_n + K·Q_n

Essa si ricava raggruppando le due celle adiacenti della prima riga in cui compare 1 e le due celle della seconda riga poste in prima e quarta colonna.

9. Applicazioni dei flip-flop

I flip-flop trovano applicazione in tutti i circuiti digitali sequenziali, cioè in quei circuiti in cui le uscite, oltre a dipendere dagli ingressi esterni, dipendono anche dallo stato interno assunto in precedenza. In altre parole trova applicazione in tutti i dispositivi di memoria: contatori, centralina dei cancelli automatici, ascensori, lavatrici, antifurto, generatori di sequenze binarie e, in particolare, in tutte le applicazioni di automazione industriale.

9.1. Comandi separati di marcia e di arresto
A titolo d'esempio si mostra in fig.12 un flip-flop SR con ingressi in logica negativa realizzato con due porte NAND comandato da due pulsanti, normalmente aperti, indicati con PM e PA. Il circuito consente i comandi separati per la marcia e l'arresto di apparati di potenza.

Quando i pulsanti sono nello stato di riposo, gli ingressi del flip-flop sono al livello logico alto: l'uscita conserva lo stato precedente.

Per mettere in marcia il circuito di potenza, ovvero porre Q=1, si deve pigiare il pulsante di marcia PM.
Ciò provoca il collegamento a massa del pin 1 e quindi l'uscita Q si porta al livello logico alto: il circuito di potenza viene attivato.
Rilasciando il pulsante l'uscita conserva lo stato Q=1 e l'impianto rimane in marcia.
Per arrestare l'impianto si deve pigiare il pulsante di arresto PA. Ciò provoca il collegamento a massa del piedino 5 e quindi Q=0.
L'impianto si arresta. Rilasciando il pulsante l'uscita conserva lo stato Q=0 e l'impianto rimane nello stato di arresto.

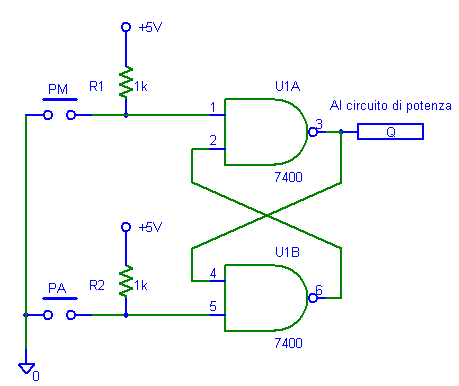
Fig.12. - Flip-flop SR per la marcia e l'arresto di apparati.

9.2. Circuito antirimbalzo
Una variante del circuito precedente consente la realizzazione di un circuito in grado di sopprimere rimbalzi meccanici dovuti ai contatti mobili di interruttori.  I rimbalzi multipli, infatti, generano un numero imprecisato di impulsi indesiderati che potrebbero far funzionare in modo anomalo il circuito dipendente dall'interruttore. Si pensi, ad esempio, al contatore "elimina code" dei supermercati. Quando il salumiere preme il pulsante, il display a due cifre deve mostrare il numero successivo a quello corrente grazie alla presenza di un circuito contatore digitale. Se, però, l'interruttore non è protetto da circuito antirimbalzo, alla pressione dello stesso da parte del salumiere, si generano più impulsi che verrebbero conteggiati e quindi anziché visualizzare il numero successivo, vedremmo sui display un numero sicuramente più grande. Se, ad esempio, il display mostra il numero 30 ed alla pressione dell'interruttore si generano 5 impulsi, il successivo numero visualizzato sul display sarà 35 anziché 31.
Un possibile circuito antirimbalzo si realizza con lo schema logico di fig.13 che impiega un flip-flop S R a porte NAND.

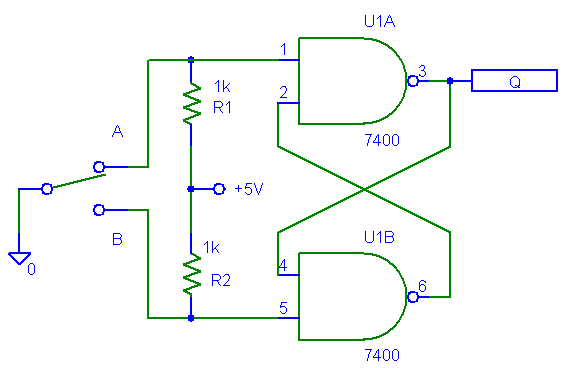
Fig.13.- Il deviatore seguito dal flip-flop prende il nome di interruttore antirimbalzo. 

Il deviatore può assumere due posizioni: A e B. Il contatto mobile è collegato alla massa e perciò porta il livello logico 0 all'ingresso collegato.
Supponiamo che il deviatore passi da A a B e successivamente ritorni nella posizione A.

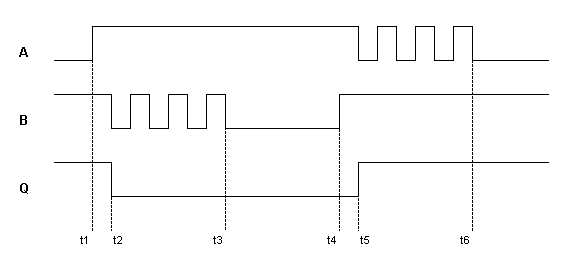
Fig.14. - Forme d'onda nei punti A, B e sull'uscita Q.

Nell'istante t1 il contatto mobile lascia il punto A e questo si porta al livello logico 1. Nell'istante t2, terminata la sua corsa, il contatto mobile tocca il punto B che si porta al livello 0. A causa della sua elasticità, la lamella vibra causando gli impulsi visibili tra gli istanti t2 e t3. In t3 la lamella tocca definitivamente il punto B. Nell'istante t4 si decide di riportare l'interruttore nella posizione A. Quando in t4 il contatto mobile lascia il punto B, questo si porta a 1 e nell'istante t5 raggiunge per la prima volta il punto A che si porta a zero. A causa dell'elasticità della lamella del contatto mobile, si creano su A delle vibrazioni che generano gli impulsi visibili sulla linea A nell'intervallo di tempo compreso tra t5 e t6. In t6 il contatto mobile tocca definitivamente il punto A che rimane definitivamente al livello logico. Nella fig.14 si è supposto che il rimbalzo meccanico produca 3 impulsi spuri prima di raggiungere definitivamente il livello logico 0.

Esaminando le forme d'onda di A e B nei vari  intervalli di tempo, si deduce facilmente la forma d'onda dell'uscita Q che, come si vede nella fig.14, è esente dai rimbalzi meccanici.

9.3 Contatore a tre bit
Si mostra in fig.15 un collegamento tra 3 flip-flop JK NET che realizzano un contatore binario a tre bit capace di mostrare su un display, ciclicamente, cifre da 0 a 7 sotto l'applicazione di un fronte di discesa applicato al clock.

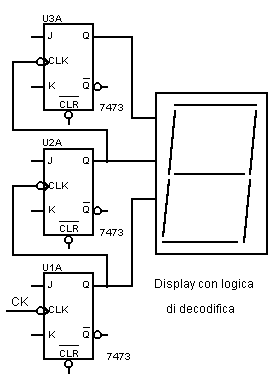
Fig.15 - Contatore a 3 bit con visualizzazione su un display. 

Gli impulsi di clock CK si applicano all'ingresso CLK del flip-flop JK denominato U1A. L'uscita Q del flip-flop U1A si applica all'ingresso CLK del flip-flop U2A e, analogamente, l'uscita Q del secondo flip-flop si applica all'ingresso CLK del flip-flop U3A. Gli ingressi J e K di tutti i flip-flop sono tenuti ad 1 per cui ad ogni fronte di discesa applicato agli ingressi CLK l'uscita Q cambia di stato.
Indicando con Q3 Q2 Q1 le uscite dei 3 flip-flop e supponendo 000 lo stato iniziale del contatore si ha, dopo l'applicazione di successivi impulsi di clock:

Applicando tali linee ad un display dotato di circuito di decodifica interno si avrà sul visualizzatore la comparsa delle cifre da 0 a 7.
Dopo il 7 riapparirà nuovamente lo 0 e così via. Le linee CLR, se portate allo 0 logico, azzerano il contatore indipendentemente dal clock (comando asincrono).

9.4. Flip-flop D per la rivelazione del verso di rotazione di un disco.
Su un disco metallico vengono praticate due fenditure semicircolari sfalsate fra di loro di 1/4 di giro come si mostra nella fig.16. Da parti opposte al disco sono inserite due sorgenti di luce (diodi LED) e due fotorivelatori S1 e S2 in grado di trasformare in forma binaria le zone opache e trasparenti delle semicorone circolari A e B (00 01 11 10).

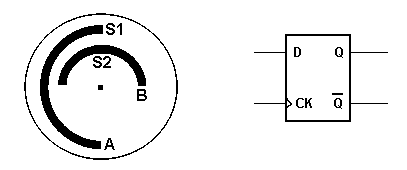
Fig.16. - Encoder e flip flop per il rilievo del verso di rotazione.

Applicando il bit B all'ingresso D del flip-flop ed il bit A all'ingresso di clock, l'uscita Q è in grado di rivelare il verso di rotazione del disco.
Infatti nel caso in cui il disco ruota in senso orario si ottiene per il bit A e B la seguente sequenza: AB = 00 01 11 10.
Se, invece, il disco ruota in senso antiorario, si ottiene: AB = 00 10 11 01.

In fig.17 si mostrano le forme d'onda da cui si deduce che, nel caso di rotazione in senso orario, i fronti di salita applicati al clock durante gli istanti t1, t2, ... vedono la linea B applicata all'ingresso D di valore 1 e quindi si ottiene Q=1, viceversa durante la rotazione antioraria i fronti di salita presenti all'ingresso di clock durante gli istanti t3, t4,... vedono la linea D al valore 0 e quindi Q=0.

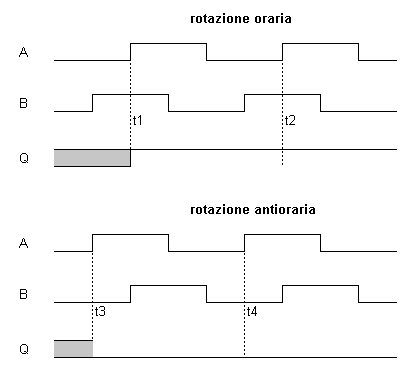
Fig.17. -  Forme d'onda.

Contatore sincrono UP/DOWN mod.8
a cura del prof. Giuseppe Spalierno docente di Elettronica e Sistemi presso l'I.T.I. "Modesto PANETTI" di BARI

1. Premessa

Un contatore digitale si dice sincrono se il clock esterno è applicato simultaneamente agli ingressi di clock di tutti i flip - flop che lo costituiscono.

Un contatore mod.8 in avanti (UP) consente di ottenere, in forma binaria, la sequenza di numeri compresi tra 0 e 7, come si mostra nel diagramma degli stati di fig.1, cioè le configurazioni binarie comprese tra 000 e 111. Sono, pertanto, necessari 3 flip-flop che sceglieremo di tipo J-K non importa se PET (Positive Edge Triggered) o NET (Negative Edge triggered).

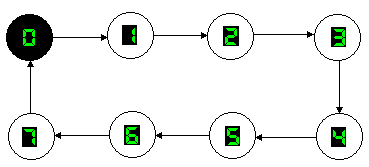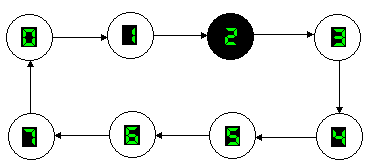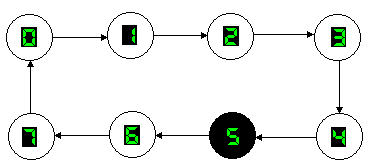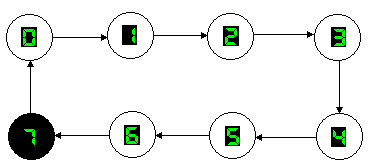
Fig.1 Diagramma degli stati per un contatore UP mod.8.

Un contatore mod.8 indietro (DOWN) consente di ottenere, in forma binaria, la sequenza di numeri compresi tra 7 e 0, come si mostra nel diagramma degli stati di fig.2, cioè le configurazioni binarie comprese tra111 e 000. Sono, pertanto, necessari 3 flip-flop che sceglieremo di tipo J-K non importa se PET (Positive Edge Triggered) o NET (Negative Edge triggered).

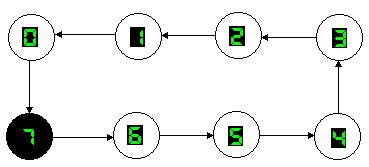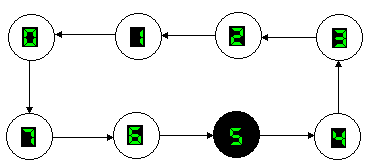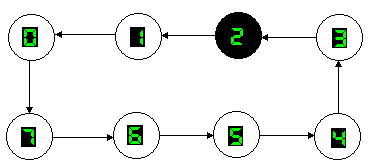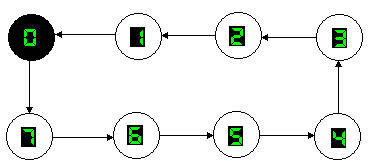
Fig.2 Diagramma degli stati per un contatore down mod.8.

Un contatore UP/DOWN consente di comandare la sequenza di conteggio in senso crescente (UP) o decrescente (DOWN). Il contatore UP (in avanti) a tre bit conta da 0 a 7; il contatore DOWN (indietro) conta da 7 a 0. Una linea digitale esterna U/D consente di selezionare la direzione del conteggio.

Si mostra, di seguito, la tabella delle transizioni che il contatore deve rispettare.

Tabella delle transizioni per un contatore UP ed un contatore DOWN entrambi binari a 3 bit

2. Equazioni di funzionamento

Il metodo di progettazione dei contatori sincroni porta alle seguenti funzioni da applicare agli ingressi J e K dei flip-flop utilizzati.

a) contatore sincrono binario UP a 3 bit:

J1=1, K1=1 per il flip-flop meno significativo; 

J2=Q1, K2=Q1 per il secondo flip-flop; 

J3=Q2·Q1, K3=Q2·Q1 per il flip - flop più significativo. 

b) contatore sincrono binario DOWN a 3 bit:

J1 = K1 = 1   per il flip-flop meno significativo; 

J2 = K2 = Q1   per il secondo flip-flop; 

J3 = K3 = Q2·Q1    per il flip - flop più significativo. 

c) contatore sincrono binario UP/DOWN a 3 bit:

J1 = K1 = 1

 per il flip-flop meno significativo (come nei casi precedenti); 

   J2 = K2 = Q1·U/D + Q1·U/D  per il secondo flip - flop; 

J3 = K3 = Q2·Q1·U/D +Q2· Q1·U/D  per il flip -flop più significativo. 

In altre parole, gli ingressi del secondo flip -flop J2 e K2 sono pilotati dall'uscita di un MUX (multiplexer) i cui due ingressi (Q1 e Q1) sono le uscite del primo flip -flop e gli ingressi del terzo flip-flop J3 e K3 sono pilotati dall'uscita di un altro MUX avente come ingressi Q2·Q1 e Q2·Q1 .
 

3. Simulazione con il programma DesignLab Ev.8 della MicroSim o PSpice 9.2 

In fig.3 si mostra lo schema elettrico realizzato in ambiente Schematic.

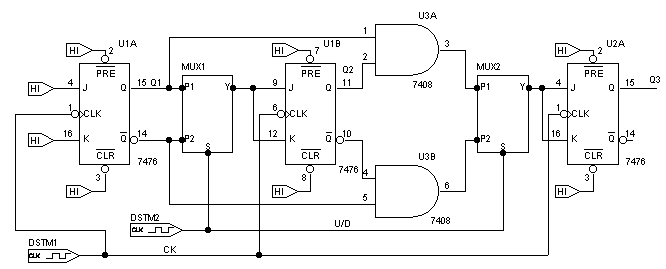
Fig.3 Schema logico del contatore sincrono UP/DOWN a tre bit.

Particolare attenzione merita il MUX realizzato tramite il comando DRAW/BLOCK.
Dopo aver editato il comando DRAW/BLOCK appare, sul foglio di lavoro, la sagoma di un rettangolo che, successivamente si potrà ridimensionare a piacere.
Il blocco così definito assume il nome HR1 che possiamo cambiare, ad esempio, in MUX1 semplicemente cliccando due volte in rapida successione sul testo HR1.
Il blocco deve possedere tre ingressi che chiameremo P1, P2, S e una uscita che chiameremo Y.
Per definire queste 4 linee digitali è sufficiente disegnare una linea dalla sinistra del blocco fino all'interno del blocco: il programma disegna un nodo sul lato sinistro del blocco che denomina P1 (ci sta bene).
Ripetiamo il tracciamento di una linea più in basso dall'esterno all'interno del blocco. Il programma denomina P2 il nodo che fa apparire.
Tracciamo ancora una linea che termina sul lato inferiore del blocco e il nodo P3 inserito dal programma lo rinominiamo S.
Tracciamo, infine, una linea che termina sul lato destro del blocco e il nodo P4 lo denominiamo Y.
Terminato il disegno del blocco si procede alla realizzazione dello schema logico che lo rappresenta.
Facciamo doppio click in rapida successione all'interno della sagoma del blocco.
Ci viene chiesto di definire il nome del file che conterrà il circuito logico che ci apprestiamo a sviluppare. Decidiamo di chiamare tale file col nome MUX.SCH.
Ci appare un foglio vuoto di Schematic che presenta, però, quattro connettori di nome P1, P2, S e Y.
Realizziamo lo schema elettrico come quello mostrato in fig.4.

Fig.4 Realizzazione a porte NAND di un MUX a 2 ingressi.

Al termine della realizzazione del circuito di fig.4 si ritorna al livello superiore, nello schema di fig.3, tramite il comando NAVIGATE/POP.
Poiché ci servono due multiplexer, procediamo selezionando il blocco MUX1 (click all'interno del blocco) e ricorriamo al copia ed incolla. Il secondo blocco, ovviamente, sarà ridenominato come MUX2.

4. Impostazione della simulazione

Per ottenere il generatore di clock DSTM1 avente all'interno la dicitura CLK, si attiva il comando DRAW/GET NEW PART (oppure CTRL+G) e si digita, nel campo part name, DigClock.
Doppio click nel DigClock per definire ONTIME=0.5us e OFFTIME=0.5us (peraltro già preimpostati).
La linea U/D, per la selezione della direzione del conteggio, viene applicata all'ingresso S dei due MUX ed è definita da un altro generatore di clock, DSTM2 avente ONSTATE=10us e OFFSTATE=10us.
In tal modo il contatore conterà in avanti per 10 impulsi di clock e indietro per altri 10 impulsi di clock nell'intervallo di tempo di 20 us.
Se si decide di inizializzare a zero i flip-flop il contatore assumerà i seguenti valori come mostrato in fig.5.
Per ottenere la simulazione del funzionamento come in fig.3 fare come segue:

1. si attiva il comando ANALYSIS/SETUP,
2. si clicca sul pulsante DIGITAL SETUP;
3. nella maschera flip - flop initialization si attiva all 0 ;
4. si clicca su OK;
5. si abilita la casella transient;
6. si clicca sul pulsante transient e si definiscono i seguenti valori:
1. print step = 200ns;
2. final time= 20us;
7. si termina con OK e successivamente con CLOSE.

Si può procedere alla simulazione attivando il comando ANALYSIS/SIMULATE (oppure il tasto funzione F11).

Se tutto è stato realizzato correttamente si entra in Probe e, tramite il comando Trace add, si inseriscono le linee indicate sulla parte sinistra della fig.5.

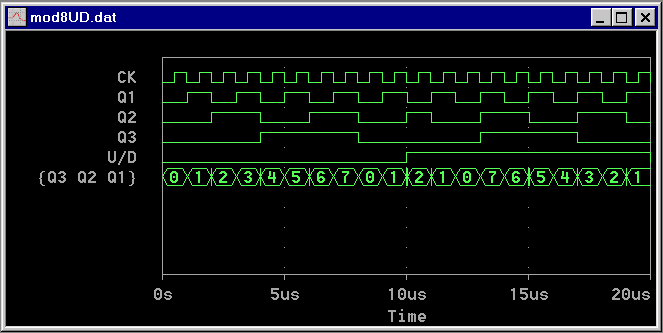
Fig.5 Forme d'onda del contatore sincrono UP/DOWN a tre bit ottenute col programma Probe.

Si osservi, infine, che per ottenere la rappresentazione in decimale del valore delle linee Q3 Q2 Q1, queste ultime devono essere rappresentate in un gruppo delimitato dalle parentesi graffe.

Dall'esame delle forme d'onda si evince che, quando U/D=0, il contatore conta in avanti e si incrementa quando il segnale di clock compie la transizione negativa (passaggio dallo stato logico alto a quello basso); quando, invece, U/D=1 il contatore conta indietro e si decrementa, anche in questo caso, durante la transizione negativa del clock.

5. Osservazioni

Un'analisi più attenta dei risultati porta ad osservare degli spike nella configurazione decimale del contatore in corrispondenza del passaggio da un numero dispari ad un numero pari durante il conteggio UP e del passaggio da un numero pari ad un numero dispari durante il conteggio DOWN.

Ciò è dovuto ai diversi tempi di ritardo di propagazione dei flip-flop: t_pLH=16ns e t_pHL=25ns (tipici valori della TTL standard. Le serie commerciali TTL più moderne presentano tempi di ritardo di propagazione più brevi).

Il passaggio, ad esempio, dal numero 1 (001) al 2 (010) durante il conteggio UP, comporta la contemporanea commutazione da parte di Q2 e Q1. In questo caso Q2 è più veloce perché per passare da 0 a 1 impiega 16ns mentre Q1 prima di passare da 1 a 0 impiega 25ns. Per 9ns risultano a 1 sia Q2 che Q1. In tale intervallo di tempo il contatore fornisce il valore 011 che corrisponde a 3.

Riassumendo: nonostante il contatore sia sincrono, si ottiene per quasi il 50% delle commutazioni, una non corretta modalità di conteggio. Abbiamo appena visto che il passaggio da 1 a 2 avviene secondo la sequenza 1 - 3 - 2; lo stato 3 è instabile e decade spontaneamente nello stato 2 dopo un tempo di 9ns (decisamente trascurabile per la maggior parte delle applicazioni