ESERCITAZIONE (Exercise): DETERMINAZIONE SPETTRO SEGNALE(determination spectrum signal): SCHEMA ELETTRICO (Electrical Plane)

elettronica

ESERCITAZIONE (Exercise):

DETERMINAZIONE SPETTRO SEGNALE(determination spectrum signal):

SCHEMA ELETTRICO (Electrical Plane):

IMMAGINI EFFETTUATE IN LABORATORIO

TABELLA (Chart):

Valori teorici (Theorical value):

Valori calcolati (Calculed value):

APPARECCHI ED ATTREZZATURE (Tools and equipment):

RELAZIONE (Report):

CALCOLI EFFETTUATI (Effected Calculations):

Per calcolare la frequenza abbiamo dovuto utilizzare la seguente formula:

f₀=1/T

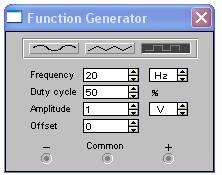
dove T assumeva un valore pari a 50 μs; quindi 1/50 * 10⁶ = 20 kHz.

Dopo aver effettuato il calcolo della frequenza abbiamo dovuto ricavare tutte le armoniche dispari affinche ci accorgessimo che i valori andassero man mano avvicinandosi.

Quindi abbiamo utilizzato la seguente formula:

A_n= 2 V_pp / nπ

Una volta effettuati questi calcolo ci siamo ricavati la frequenza di risonanza e la formula utilizzata è la seguente:

R = 1 / 2 πfC

Essenso C un'incognita e noto R ci siamo ricavati dalla formula inversa C sostituendo a C la R.

PREMESSE TEORICHE (Theorical introductions):

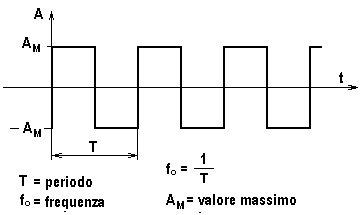Un segnale di particolare interesse nel campo delle telecomunicazioni è certamente l'onda quadra per via dei numerosissimi impieghi che la caratterizzano oggi come il clock di tutti i computer del mondo, di tutti gli orologi digitali, di tutte le portanti numeriche,  come segnale base di tutti i processi digitali e così via.

Dall'applicazione delle formule della serie di Fourier risulta che l'onda quadra in oggetto è costituita dalla somma di infinite sinusoidi, dette armoniche, di frequenza multipla intera di fo e di ampiezza data dai valori:

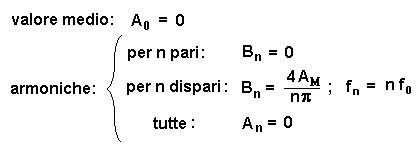
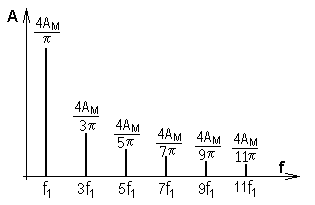
Lo spettro di ampiezza del segnale dato risulta allora quello indicato di seguito:

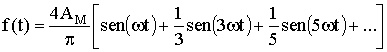La funzione sviluppata in serie di Fourier risulta allora espressa come segue:

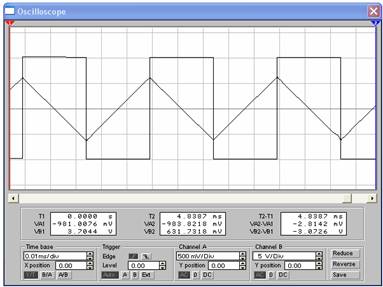
Il segnale può essere studiato dunque da due punti di vista diversi. 

Nel dominio del tempo, attraverso la sua forma d'onda.   Lo strumento idoneo per questo studio è l'oscilloscopio

Nel dominio della frequenza attraverso il suo spettro. Lo strumento idoneo in questo caso è l'analizzatore di spettro.

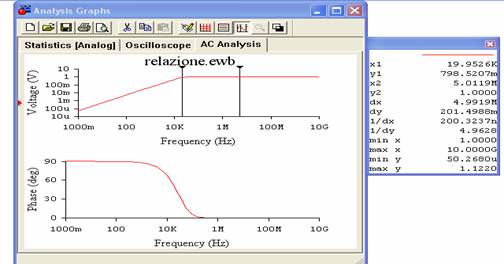
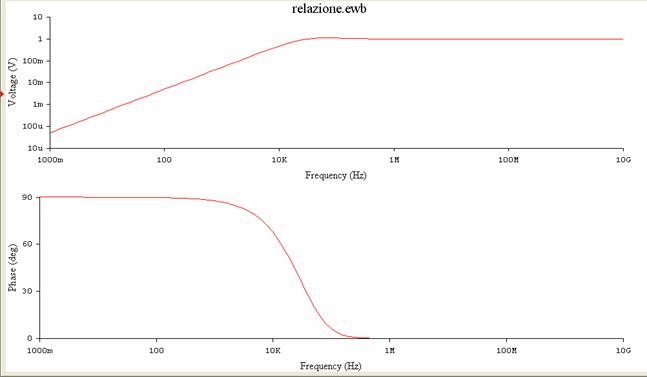
SPIEGAZIONE DIAGRAMMA DI BODE (Explanation bode's diagrams):

I diagrammi di bode rappresentano l'andamento  del segnale nel filtro attivo passa alto e abbiamo visto che la f.d.t nel diagramma del modulo si avvicina a quella teorica infatti e poco superiore a 19.5 KHz mentre quella teorica era pari a 20 KHz.

SIMULAZIONE CON WORKBENCH (Workbench simulation):

CONCLUSIONI (Conclusion): 

DIAGRAMMI DI BODE (Bode's diagram):

COMMENTI DEL PROFESSORE (Remark of teacher):

FRATTAIOLI PIETRO