|
|
| |
RISOLUZIONE DI PROBLEMI E INTELLIGENZA ARTIFICIALE.
La risoluzione dei problemi comprende tutta l'informatica.
I metodi di risoluzione dei problemi fanno uso del concetto di ricerca per tentativi, ricercando una soluzione in uno spazio di soluzioni possibili.
Presentazione dei più importanti metodi di risoluzione di problemi basati sulla ricerca per tentativi.
ROMPICAPO E GIOCHI COME ESEMPIO DI PROBLEMI
Definizione di problemi mediante esempi.
Il gioco del quindici.
Questo gioco consiste di 15 tessere mobili numerate, inserite in un telaio 4x4. Una cella del telaio è sempre vuota, cosicché è possibile spostare una tessera numerata adiacente nella cella vuota. Il problema è di mutare la disposizione iniziale in quella finale con tutte le tessere poste in modo progressivo.
STATI E OPERATORI DEI PROBLEMI
Una soluzione nel gioco del quindici è di tentare varie mosse finché non capiti di ottenere la disposizione finale, un tentativo del genere implica essenzialmente una ricerca per tentativi.
Per discutere i metodi risolutivi di questo tipo è utile introdurre la nozione di stato e operatore del problema.
- Nel gioco del quindici uno stato del problema è semplicemente una particolare disposi 727f54h zione delle tessere.
- Un operatore trasforma uno stato in un altro, nel gioco del quindici ci sono quattro operatori corrispondenti alle mosse: muovi lo spazio vuoto a sinistra, in alto, a destra, in basso.
Lo spazio degli
stati raggiungibili dallo stato iniziale consiste di tutte le disposizioni che
si possono produrre movendo le tessere nel modo corretto.
RIDUZIONE DI PROBLEMI A SOTTOPROBLEMI
Un metodo di risoluzione di problemi un po' più raffinato richiede la nozione di sottoproblema.
Per esempio, poniamoci il problema di dover guidare un'auto da Salerno a Milano. Il tutto si potrebbe ridurre ai seguenti sottoproblemi:
guidare da Salerno a Napoli
guidare da Napoli a Roma
guidare da Roma a Milano
La soluzione di tutti e tre i sottoproblemi produrrebbe la soluzione del problema originario.
Possibilità di risolvere i sottoproblemi con un metodo qualsiasi. Si può affrontare con il metodo dello spazio degli stati o analizzarlo a sua volta in sottoproblemi.
LA RAPPRESENTAZIONE E LA RICERCA
I metodi di risoluzione che abbiamo menzionato richiedono un'azione di ricerca della soluzione.
Quindi è indispensabile condurre tali ricerche nel modo più efficiente possibile.
Lo stesso problema può ammettere diverse rappresentazioni, alcune delle quali con uno spazio degli stati molto più piccolo delle altre.
Descrizioni degli stati e della forma
Definizioni degli operatori
Definizione degli stati finali
Descrizioni degli stati
Schematizzare gli stati del problema.
Scegliere una particolare forma per la descrizione degli stati
Scelta della forma
Produzioni
Operatori - funzioni
Operatori che mutano uno stato in un altro in funzione dell'input
Funzioni di descrizioni i cui valori sono nuove descrizioni
Operatori - Produzioni
Si usano :
quando le descrizioni degli stati sono in forma di stringhe
la soluzione e' una stringa
Fa uso di regole di riscrittura ( produzioni )
Un insieme di regole di
riscrittura definisce i modi un cui una stringa può essere trasformata in
un'altra
Regola di riscrittura
Per ogni occorrenza del simbolo A può essere rimpiazzato dal simbolo B.
Il segno $ sta per una sottostringa arbitraria ( anche stringa vuota )
Stati finali
Le procedure di ricerca generano nuove descrizioni
Controllare se una descrizione di stato coincide con una descrizione di stato finale assegnata
Controlli più complessi sull'ottimalita' della soluzione trovata, ritrattando il problema fino a quando non se ne trovi una ottima.
METODI DI RICERCA NELLO SPAZIO DEGLI STATI
Formulando i problemi nello spazio degli stati si può ottenere una soluzione applicando gli operatori alle descrizioni degli stati fino ad ottenere un'espressione che descrive lo stato finale.
Processi di Ricerca nei Grafi
Il linguaggio dei grafi è molto utile per la descrizione d'efficienti strategie di ricerca nello spazio degli stati.
Il principio su cui si basano tutte le rappresentazioni che vedremo è il seguente:
Si associa un nodo di partenza alla descrizione dello stato iniziale
Si calcolano tutti i successori di un nodo mediante gli operatori applicabili alla sua descrizione di stato. Tale operazione è detta espansione
Si creano i puntatori da ogni nodo al suo genitore
Si controllano le descrizioni dei nodi successori per vedere se corrispondono a quella di uno stato finale. In questo caso si può ottenere un cammino risolutivo attraversando i puntatori che dal nodo portano alla radice. In caso contrario si continua il processo di espansione.
Tuttavia una descrizione completa di un processo di ricerca deve contenere anche il criterio di espansione dei nodi. Dal differente criterio adottato si possono individuare sostanzialmente due famiglie di procedimenti, una detta di ricerca cieca ed un'altra basata sulla conoscenza euristica.
Ricerca cieca: l'espansione dei nodi avviene seguendo un ordine prestabilito dal metodo di ricerca (es. ricerca in ampiezza o ricerca in profondità) e non è influenzata dalla posizione dell'obiettivo.
Ricerca basata su conoscenza euristica: l'espansione dei nodi non avviene seguendo un ordine prestabilito ma con l'aiuto appunto di una base di conoscenza utile alla scoperta (euristica). Vengono quindi espansi prima i nodi "più promettenti" ovvero quelli che, sulle basi della nostra conoscenza, dovrebbero portarci prima ad uno stato finale.
La discussione e l'esposizione di tali metodi di ricerca avverrà limitando, senza perdita di generalità, la nostra attenzione agli alberi e non ai grafi, permettendoci di cogliere gli aspetti principali delle ricerche avendo a disposizione una struttura più chiara.
Metodi di ricerca in ampiezza
I metodi di ricerca in ampiezza espandono i nodi nell'ordine in cui questi sono generati.
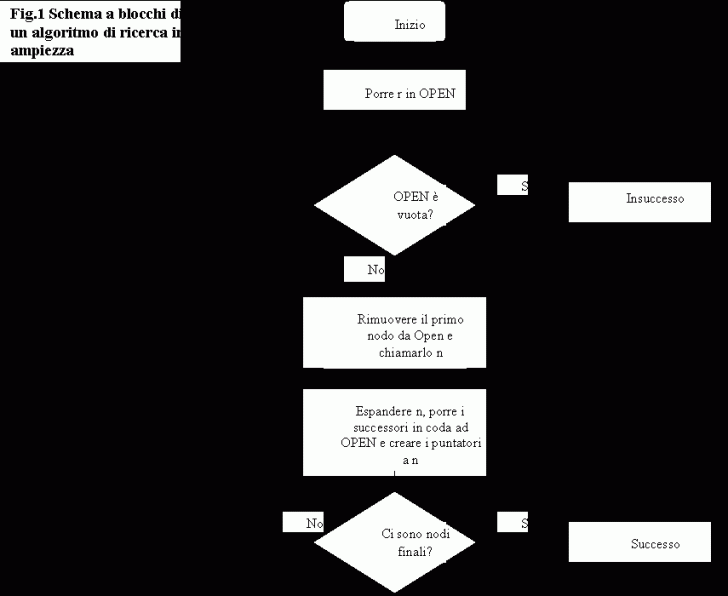
Un semplice algoritmo per la ricerca in ampiezza si basa sull'utilizzo di una coda, che chiameremo OPEN, in cui vengono inseriti i nodi da espandere (in condizioni iniziali sarà presente solo la radice). Da ogni nodo presente in questa lista vengono generati i suoi successori, verificate le condizioni di stato finale per ognuno di loro e, nel caso non si sia raggiunto nessuno stato finale, verranno a loro volta inseriti in coda ad OPEN per una futura espansione.
Possiamo vedere un semplice schema a blocchi per un algoritmo di questo tipo in Fig.1
Metodi del costo uniforme
Una versione del metodo di ricerca in ampiezza prevede che ad ogni espansione sia assegnato un costo e, come soluzione finale, restituisce un cammino a costo minimo dal nodo di partenza al nodo finale. Tale metodo è detto del costo uniforme.
E' quindi necessario tener conto di una funzione costo c(ni , nj) che indica il costo del trasferimento dal nodo ni al successore nj. Il costo del cammino generato dalla radice r al nodo n verrà indicato con g(n) e, nel caso degli alberi, sarà sicuramente il minimo costo da r a n (in quanto esiste un solo cammino).
Il metodo del costo uniforme espande i nodi secondo valori crescenti di g(n).
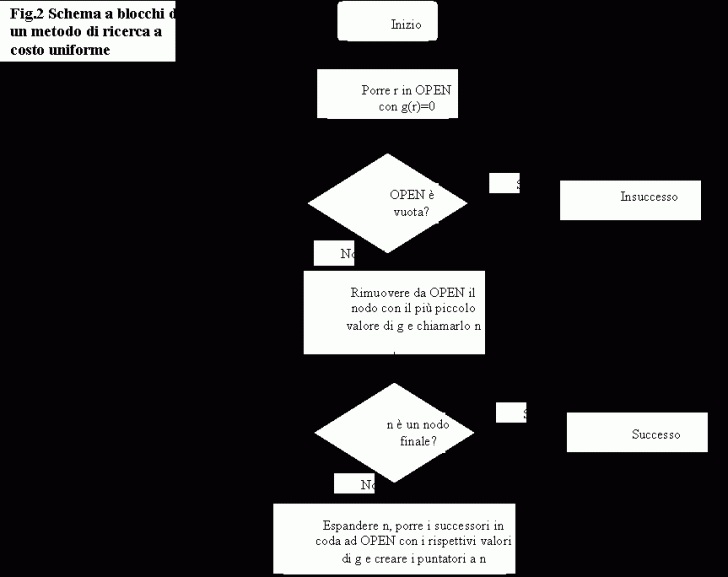
Il principio su cui lavora tale metodo è quindi simile al precedente, la differenza sostanziale sta nell'estrazione del nodo da espandere dalla lista OPEN che non avviene più in modo da selezionare il primo della lista ma estraendo il nodo con più piccolo valore di g(n) (eventuali conflitti possono essere risolti arbitrariamente).
Mostriamo in Fig.2 lo schema a blocchi di tale metodo di ricerca.
Metodi di ricerca in profondità
La ricerca in profondità è un altro metodo di ricerca cieca, il suo criterio di espansione dei nodi è caratterizzato dal fatto che viene espanso per primo l'ultimo nodo generato.
Per l'analisi di tale metodo è utile definire il concetto di profondità dei nodi in un albero.
Possiamo definire la profondità in questo modo:
La profondità della radice è zero
La profondità di un nodo interno è uguale alla profondità del suo genitore più uno.
E' da notare che questo procedimento può spingersi lungo un cammino in modo indefinito senza portare a nessun risultato. Prevedere una procedura di backtracking diventa molto utile.
Un'idea generale potrebbe essere quella di assegnare un limite massimo di espansione lungo un cammino, superato il quale, la procedura di ritorno fa in modo di espandere il nodo con profondità maggiore a disposizione ma che ancora non abbia superato tale limite.
Una procedura per questa ricerca segue gli stessi passi di quelle per la ricerca in ampiezza, ovviamente i nodi generati (non finali) vengono messi in cima alla lista OPEN per essere presi in considerazione per primi al prossimo passo di espansione. Necessario un controllo sul limite della profondità raggiunta ad ogni passo.
In Fig.3 è riportato uno schema a blocchi per tale metodo di ricerca.
Fig.3 Schema a blocchi di un metodo di ricerca in profondità



No

MODIFICHE RICHIESTE DALLA RICERCA NEI GRAFI
Le modifiche necessarie da apportare agli algoritmi di ricerca quando si eseguono nei grafi sono:
METODO DI RICERCA IN AMPIEZZA
Richiede di poter riconoscere se un nodo generato si trova già in OPEN o CLOSED in seguito ad una precedente espansione.
ALGORITMO A COSTO UNIFORME
Si associa ai nodi OPEN il più piccolo valore di g trovato fino a quel momento.
Il puntatore uscente da un nodo deve essere diretto al genitore del nodo che si trova sul cammino meno costoso trovato fino a quel momento.
Se un successore appena generato si trova già in CLOSED, si poterebbe pensare che il suo valore di g può essere inferiore, rendendo necessario lo spostamento del puntatore.
ALGORITMO DI RICERCA IN PROFONDITÀ
Se la profondità di un nodo è posto pari alla profondità del genitore meno profondo più uno, con la profondità del nodo di partenza uguale a zero, si potrebbe ottenere una ricerca in profondità scegliendo per l'espansione il nodo più profondo di OPEN.
Quando vengono generati successori che già si trovano in OPEN o in CLOSED potrebbe essere necessario reticolare la profondità.
DISCUSSIONE DELLA CONOSCENZA EURISTICA
I metodi di ricerca in ampiezza e in profondità sono metodi esaustivi per la ricerca di un cammino, ma troppo dispendiosi in termini di tempo e di memoria.
E' possibile enunciare principi e regole che aiutano a ridurre lo sforzo di ricerca facendo perdere la certezza di trovare un cammino a costo minimo in corrispondenza di alcuni o tutti i problemi.
Un metodo flessibile (ma costoso), applicato alla ricerca in profondità, consiste nel piazzare i successori appena generati all'inizio di OPEN in un ordine ben definito dalla conoscenza euristica cosi che la ricerca in profondità espanda ad ogni passo il successore ritenuto più adatto. Per applicare una simile procedura di riordinamento è necessario poter misurare quanto un nodo sia "promettente" con una funzione di valutazione.
SCOPO DELLA FUNZIONE DI VALUTAZIONE:
Fornire un metodo di classificazione dei nodi candidati all'espansione che permetta di determinare quale nodo si trova più probabilmente sul miglior cammino verso l'obiettivo.
Supponiamo di avere una funzione f che possa essere usata per ordinare i nodi in vista della loro espansione, allora f(n) denota il valore della funzione al nodo n.
Se si ordinano i nodi da espandere secondo valori crescenti di f, si può usare un algoritmo che sceglie per la prossima espansione il nodo di OPEN con il più piccolo valore di f supponendo che il nodo con la valutazione più bassa abbia la massima probabilità di trovarsi sul cammino ottimo.
I risultati della ricerca dipendono in modo critico dalla scelta della funzione di valutazione:
L'uso di una funzione di valutazione che ignori la promessa verace di certi nodi può portare a cammini di costo non minimo
D'altra parte l'uso di una funzione di valutazione che creda con troppa facilità alle promesse di tutti i nodi, porta all'espansione di troppi nodi.
La linea generale che questo metodo adotta,consiste nel ragionare all'indietro.
Partendo da un problema originario lo si suddivide in sotto-problemi
I sotto-problemi in sotto-problemi più piccoli ..
Sino ad arrivare a problemi primitivi banali.
Questo gioco si può risolvere
semplicemente mediante la riduzione a sottoproblemi. Un modo per ridurlo è: per portare i dischi sul piolo 3, bisogna prima
portarvi il disco C, ma ancora prima bisogna che il piolo 3 sia libero. per spostare C, bisogna spostare prima A e B. Ma
per portare C sul piolo 3, bisogna che A e B, siano spostati sul piolo 2 ora possiamo spostare C dal piolo 1 al 3, e poi
spostare A e B
Per meglio capire come viene effettuato questo
metodo, prendiamo ad esempio il gioco della Torre di Hanoi
![]()
![]()
![]()
![]()
![]()
![]()
C B A
![]()
![]()
![]()
![]()
![]()
inizio obiettivo
![]()
![]()
![]()

I tre sottoproblemi, sono più semplici da risolvere rispetto al problema originario
In effetti il problema 3, è un problema primitivo che consiste di una sola mossa
Ripetendo il ragionamento per i punti 1 e 2, possiamo portare anche questi a problemi primitivi
Il metodo della riduzione a sottoproblemi impegna operatori che trasformano descrizioni di problemi in descrizioni di sottoproblemi
Spesso conviene descrivere un problema in termini di una rappresentazione nello spazio degli stati
Ogni problema nello spazio degli stati può essere rappresentato come:
S : l'insieme dei nodi di partenza
F : l'insieme degli operatori che mandano descrizioni di stato in descrizioni di stato
G : l'insieme degli stati finali
La terna (S,F,G) definisce un problema e può essere usata come sua descrizione
Un operazione di riduzione a sottoproblemi trasforma la descrizione di un problema in un insieme di problemi ridotti o successori
La trasformazione di tutti i problemi successori,comporta la soluzione del problema genitore
Per ogni descrizione ci possono essere molti operatori di deduzione applicabili, ognuno che produce soluzioni alternative di sottoproblemi
Possono esserci sottoproblemi che non ammettono soluzioni, in questo caso è necessario provare diversi operatori prima di produrre un insieme che sia pienamente risolvibile
Una classe di problemi consiste nel dimostrare che certi enunciati sono veri
Esempio:
Sia S l'enunciato da verificare e T premesse assunte vere
S|T
Nella soluzione del problema aggiungiamo N premesse per ottenere l'insieme dei problemi ridotti:
S|T, X1, X2, ..Xn
X1|T, X2, X3.......Xn
Xn|T
dove X1...Xn sono premesse addizionali
Lo scopo di tutte le riduzioni a sottoproblemi è di arrivare a sottoproblemi primitivi le cui soluzioni sono ovvie.
Per soluzioni ovvie, s'intendono sia soluzioni che si risolvono in una mossa sola, o problemi più complessi di cui già si conosce la soluzione
Lo scopo del processo di ricerca su un grafo AND/OR è di dimostrare che il nodo di partenza è risolto
La definizione di nodo risolto si può dare ricorsivamente:
i nodi terminali sono risolti (perché associati a problemi primitivi)
se un nodo non terminale ha successori OR, esso è risolto se e solo se almeno uno dei suoi successori è risolto
se un nodo non terminale ha successori AND, esso è risolto se e solo se tutti i suoi successori sono risolti
E' conveniente rappresentare la riduzione di un problema ad insiemi alternativi di problemi successori mediante una struttura simile ad un grafo.
Esempio:
Supponiamo che il problema A possa essere risolto risolvendo i problemi B e C, D ed E, o F.
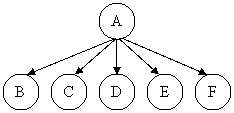
Introduciamo nella struttura nodi supplementari in modo tale che ogni insieme che contiene più di un problema successore si trova raggruppato sotto il suo nodo genitore
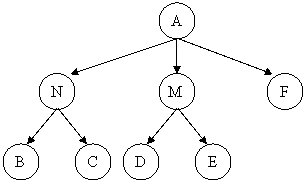
Un nodo privo di successori si dice insolubile
La presenza di un nodo insolubile può comportare l'insolubilità di anche altri nodi
La definizione generale:
i nodi terminali privi di successori sono insolubili
se un nodo non terminale ha successori OR, è insolubile se e solo se tutti i suoi successori sono insolubili
se un nodo non terminale ha successori AND, è insolubile se e solo se uno dei suoi successori è insolubile
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025