|
|
| |
Problemi di base di
Elaborazione Numerica
dei Segnali
a edizione: febbraio 1999
disponibile su rete telematica pubblica mediante
download gratuito per scopi didattici non commerciali
(1a edizione: sett. 1992; 2a edizione: sett. 1993; 3a edizione: feb. 1994)
Indice
pag.
Parte I. Operazioni su sequenze.
1. Convoluzione
1.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..6
1.2 Esempio grafico.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ...7
2. Correlazione temporale
2.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..9
2.2 Esempio grafico.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f 10
3. Espansione
3.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f 12
3.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ...............13
4. Interpolazione
4.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f 15
4.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ...............18
5. Decimazione
5.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f 19
5.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ...............21
6. Uso della trasformata continua di Fourier
6.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f 22
6.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ...............23
7. Uso della trasformata discreta di Fourier
7.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f 25
7.2 Esercizio (filtraggio mediante
sovrapposizione ed estrazione).................... 515j98f .................... 515j98f .....26
7.3 Esercizio (filtraggio mediante
sovrapposizione e somma).................... 515j98f .................... 515j98f ..............29
Parte II. La trasformata-Z.
8. Equazioni lineari alle differenze
8.1 Richiamo teorico.................... 515j98f .................... 515j98f .................... 515j98f ...................32
8.2 Esempio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ................32
9. Alcune trasformate-Z notevoli
9.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f 35
9.2 Esercizio (gradino unitario).................... 515j98f .................... 515j98f .................35
9.3 Esercizio (gradino unitario traslato).................... 515j98f .................... 515j98f 36
9.4 Esercizio (rettangolo unitario).................... 515j98f .................... 515j98f ............37
9.5 Esercizio (rampa finita).................... 515j98f .................... 515j98f .................... 515j98f .....38
9.6 Esercizio (esponenziale causale).................... 515j98f .................... 515j98f ........39
9.7 Esercizio (esponenziale anticausale).................... 515j98f .................... 515j98f 40
10. Metodo dei residui
10.1 Teorema dei residui.................... 515j98f .................... 515j98f .................... 515j98f .........42
10.2 Esercizio (poli distinti).................... 515j98f .................... 515j98f .................... 515j98f ....44
10.3 Esercizio (poli multipli).................... 515j98f .................... 515j98f .................... 515j98f ..46
10.4 Esercizio (sequenze di autocorrelazione).................... 515j98f ........49
Parte III. Filtri numerici.
11. Grafi di sistema
11.1 Premessa.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..........52
11.2 Esercizio (realizzazione in forma canonica).................... 515j98f ...52
11.3 Esercizio (sistema a traliccio).................... 515j98f .................... 515j98f ...........55
12. Filtri a fase minima
12.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................57
12.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ............58
13. Progetto mediante la trasformata inversa di Fourier
13.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................60
13.2 Esercizio (filtro derivatore).................... 515j98f .................... 515j98f ..............61
13.3 Esercizio...(filtro di Hilbert).................... 515j98f .................... 515j98f ...............63
14. Progetto mediante l'invarianza all'impulso
14.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................65
14.2 Esercizio (poli complessi coniugati).................... 515j98f ...................66
14.3 Esercizio (filtro di Butterworth).................... 515j98f .................... 515j98f .....68
15. Progetto mediante la trasformazione bilineare
15.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................71
15.2 Esercizio (poli complessi coniugati).................... 515j98f ...................72
15.3 Esercizio (filtro di Butterworth).................... 515j98f .................... 515j98f .....75
16. Progetto mediante il campionamento in frequenza
16.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................79
16.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ............81
Parte IV. Analisi statistica e stime spettrali.
17. Errori di quantizzazione
17.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................85
17.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ............87
18. Calcolo di momenti in sistemi non-lineari
18.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................91
18.2 Esercizio (quadratore).................... 515j98f .................... 515j98f .................... 515j98f .....92
19. Progetto di filtri ai minimi quadrati
19.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .................94
19.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ............96
20. Stima spettrale autoregressiva
20.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..............100
20.2 L'algoritmo ricorsivo di Levinson-Durbin.................... 515j98f ...102
20.3 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f .........104
21. Predizione lineare ottima
21.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..............106
21.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..........109
22. Relazione tra matrici di autocorrelazione e coefficienti AR
22.1 Premessa.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ........111
22.2 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..............111
23. Stima spettrale di Capon
23.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..............113
23.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..........116
24. Stima spettrale di Pisarenko
24.1 Teoria.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..............118
24.2 Esercizio.................... 515j98f .................... 515j98f .................... 515j98f .................... 515j98f ..........121
Parte V. Raccolta di esercizi riepilogativi.
25. Testi di esame di Elaborazione Numerica dei Segnali
25.1 Esercizio di marzo 1992.................... 515j98f .................... 515j98f ..................123
25.2 Esercizio del 17 marzo 1992 (primo esonero)...............124
25.3 Esercizio di aprile 1992.................... 515j98f .................... 515j98f ...................125
25.4 Esercizio del 12 maggio 1992 (secondo esonero).........126
25.5 Esercizio del 15 giugno 1992.................... 515j98f .................... 515j98f ........127
25.6 Esercizio del 25 giugno 1992.................... 515j98f .................... 515j98f ........128
25.7 Esercizio di luglio 1992.................... 515j98f .................... 515j98f .................... 515j98f 129
25.8 Esercizio di settembre 1992.................... 515j98f .................... 515j98f ..........130
25.9 Esercizio del 20 ottobre 1992.................... 515j98f .................... 515j98f .......131
25.10 Esercizio del 26 novembre 1992.................... 515j98f ..................132
25.11 Esercizio dell'11 gennaio 1993.................... 515j98f .................... 515j98f ..133
25.12 Esercizio del 25 febbraio 1993.................... 515j98f .................... 515j98f ..134
25.13 Esercizio del 16 marzo 1993 (primo esonero)............135
25.14 Esercizio del 5 aprile 1993.................... 515j98f .................... 515j98f ..........136
25.15 Esercizio del 18 maggio 1993 (secondo esonero)......137
25.16 Esercizio del 31 maggio 1993.................... 515j98f .................... 515j98f .....138
25.17 Esercizio del 21 giugno 1993.................... 515j98f .................... 515j98f ......139
25.18 Esercizio del 1o luglio 1993.................... 515j98f .................... 515j98f .........140
25.19 Esercizio del 12 luglio 1993.................... 515j98f .................... 515j98f ........141
25.20 Esercizio del 14 settembre 1993.................... 515j98f ..................142
25.21 Esercizio del 15 ottobre 1993.................... 515j98f .................... 515j98f ....143
25.22 Esercizio del 22 novembre 1993.................... 515j98f ..................144
25.23 Esercizio dell'11 gennaio 1994.................... 515j98f .................... 515j98f ..145
25.24 Esercizio del 25 gennaio 1994.................... 515j98f .................... 515j98f ...146
25.25 Esercizio del 16 febbraio 1994.................... 515j98f .................... 515j98f ..147
Parte I. Operazioni su sequenze.
1. Convoluzione.
1.1 Teoria.
L'operazione di convoluzione ricorre assai spesso nell'analisi dei segnali e sistemi a tempo discreto. Infatti, e' noto dalla teoria dei sistemi lineari che la sequenza in uscita ad un sistema lineare a tempo discreto invariante alla traslazione e' ottenibile come somma di convoluzione tra la sequenza di ingresso e la risposta impulsiva caratteristica del sistema stesso. In tal caso, i principi di stabilita' e fisica realizzabilita' dei sistemi reali vincolano le sequenze in gioco.
Tuttavia, piu' in generale, si puo' definire la convoluzione fra due sequenze qualunque, ovvero senza particolari ipotesi di causalita' e/o stabilita'. Formalmente, dette x(k) e y(k) le sequenze da elaborare, che si estendono da k=0 a k=M e k=N, rispettivamente, e definita z(k) = x(k) y(k) la sequenza risultante dalla loro convoluzione, si puo' scrivere la seguente relazione:

In generale, gli indici della sommatoria si estendono ai massimi valori possibili, cioe' laddove il risultato del prodotto fra le due sequenze opportunamente traslate e' diverso da zero. Ovvero, se supponiamo che x(k) e y(k) si estendano da M a M e da N a N rispettivamente, nell'eq. (1.1) l'indice i e' compreso fra max [N , k-M ] e min [N , k-M ], mentre l'indice j va dal valore max [M , k-N ] e min [M , k-N
Si noti inoltre che l'operatore di convoluzione gode della proprieta' commutativa e che la sequenza z(k) risultante dalla convoluzione si estende da M +N a M +N
1.2 Esempio grafico.
L'operazione fra sequenze ben si presta ad un calcolo di tipo grafico. A tal fine si considerino le due sequenze di fig. 1.1, supposte per semplicita' causali.
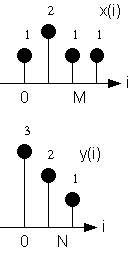
Fig. 1.1. Le sequenze originarie x(i) e y(i).
La procedura grafica di calcolo della convoluzione, illustrata nella fig. 1.2, e' la seguente. La freccia tratteggiata indica il verso di traslazione della prima sequenza dopo che e' stata invertita (verso destra per k positivi, verso sinistra se negativi). Le due sequenze, cosi' posizionate per ogni k, sono moltiplicate termine a termine; quindi, i risultati ottenuti sono sommati algebricamente (proprio come in un prodotto scalare tra due vettori). I valori cosi' ottenuti sono rappresentati graficamente in sequenza in funzione della traslazione k. Val la pena notare che invertire nel tempo i due segnali non cambia, per la proprieta' di commutativita', il risultato della convoluzione.
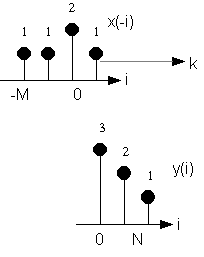
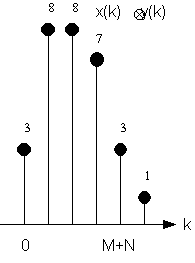
Fig. 1.2. Esempio di calcolo della convoluzione fra sequenze.
2. Correlazione temporale.
2.1 Teoria.
Anche l'operazione di correlazione temporale e' largamente usata nell'analisi ed elaborazione numerica dei segnali. Essa serve, intuitivamente, a valutare quanto due sequenze sono "simili". La sequenza di correlazione temporale e' matematicamente definita come:
![]()
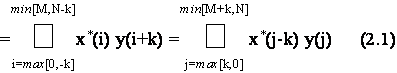
In generale, gli indici della sommatoria si estendono ai massimi valori possibili dei prodotti fra gli elementi delle due sequenze. In particolare, se le sequenze x(k) e y(k) si estendono da M a M e da N a N , rispettivamente, l'indice i varia fra il valore max [M , N -k] ed il valore min [M , N -k], mentre l'indice j si estende dal valore max [M +k , N ] fino a min[M +k , N
Fra le proprieta' della correlazione temporale, si osservi che quella commutativa non sussiste. Infatti, se si scambiano fra loro le due sequenze, si ottiene una diversa (in generale) sequenza di correlazione.
Ovviamente, quanto detto or ora non vale per la sequenza di autocorrelazione, ove le due sequenze in gioco coincidono. In questo caso, la sequenza di autocorrelazione risulta essere a simmetria coniugata (cioe' parte reale pari e parte immaginaria dispari). Cio' consente un piu' rapido calcolo del risultato (basta calcolare meta' sequenza di correlazione), nonche' un piu' agevole controllo di eventuali errori.
2.2 Esempio grafico.
Consideriamo le medesime sequenze x(i) e y(i) di fig. 1.1. La procedura grafica di correlazione consiste nelle seguenti operazioni. Le due sequenze sono moltiplicate termine a termine e quindi i risultati sono sommati per ogni k come nel caso della convoluzione (vedi eq. (2.2)), salvo che la prima sequenza deve essere in questo caso coniugata, se complessa, (invece che invertita come accadeva con la convoluzione), prima di essere traslata di k passi nel verso della freccia tratteggiata. I campioni risultanti sono rappresentati nella Fig. 2.1 in funzione della variabile temporale k.
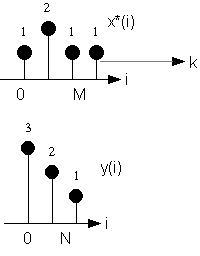
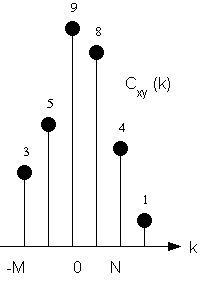
Fig. 2.1. Esempio di calcolo della correlazione temporale fra sequenze.
3. Espansione.
3.1 Teoria.
Fra le operazioni su sequenze, quella di espansione costituisce una delle piu' importanti poiche', come vederemo nel successivo capitolo, e' necessaria per effettuare l'interpolazione numerica. Essa e' una funzione del fattore di espansione F ed e' matematicamente esprimibile come:
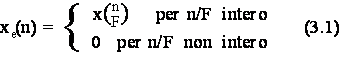
che corrisponde alla procedura grafica illustrata nella fig. 3.1 nel caso F=2.
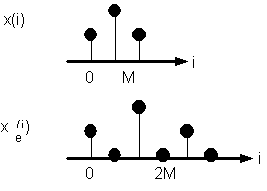
Fig. 3.1. Esempio di espansione di una sequenza di un fattore F=2.
Lo spettro della sequenza espansa Xe w) risulta, per definizione:
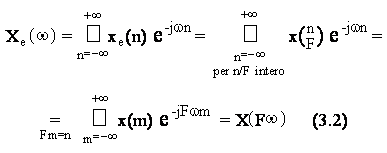
ove X(w) e' lo spettro della sequenza originaria.
L'operazione di espansione corrisponde graficamente alla compressione di un fattore F come illustrato in fig. 3.2 per F=2.
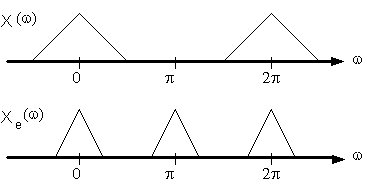
Fig. 3.2. Esempio di spettro prima e dopo l'espansione
della sequenza di un fattore F=2.
3.2 Esercizio.
Data la sequenza x(n) avente uno spettro in w pari a X(w), calcolare analiticamente lo spettro Y(w) della sequenza y(n) ottenuta nel seguente modo:
![]()
Svolgimento.
E' possibile considerare la sequenza y(n) come composta da due termini:
y(n) = xe(n) - xe(n-1)
ove xe(n) e' la sequenza x(n) espansa di un fattore 2, cioe':
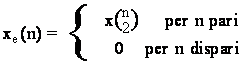
che ha uno spettro pari a:
Xe w) = X(2w
Pertanto, il risultato cercato e', per la linearita' della trasformata di Fourier:
Y(w) = X(2w) - e-jw X(2w
4. Interpolazione.
4.1 Teoria.
In molte applicazioni dell'elaborazione numerica dei segnali, l'interpolazione di sequenze riveste particolare importanza. Sovente, infatti, i segnali sono campionati con il massimo periodo possibile, compatibile con il teorema del campionamento, per aumentare la velocita' di elaborazione, ma l'utilizzazione del risultato richiede una risoluzione (numero di campioni per unita' di tempo) ben maggiore.
La formula classica che si basa sul sovracampionamento del segnale analogico ricostruito, ovvero sull'interpolazione analogica e successivo ricampionamento del segnale a tempo continuo, cioe':
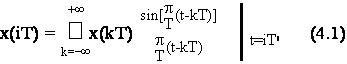
e' del tutto inadeguata per un sistema di elaborazione numerico perche', essendo implicitamente basata sull'elettronica analogica, risulta non solo troppo complessa e costosa, ma anche imprecisa (derive termiche dei componenti) e rigidamente vincolata al progetto iniziale (non e' riprogrammabile via software).
Un interpolatore numerico, ovvero realizzato con tecniche numeriche, e' implementabile come la cascata di un espansore e di un filtro numerico passa-basso ideale. La fig. 4.1 illustra lo schema a blocchi della procedura ed un esempio di applicazione per un fattore di interpolazione F=2.
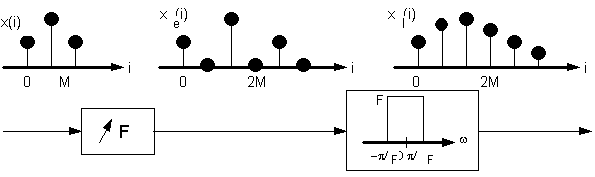 Fig.
4.1. Schema a blocchi di un interpolatore numerico (costuito dalla cascata di
un espansore e di un filtro numerico passa-basso ideale) ed esempio di
applicazione ad una sequenza con fattore di interpolazione F=2.
Fig.
4.1. Schema a blocchi di un interpolatore numerico (costuito dalla cascata di
un espansore e di un filtro numerico passa-basso ideale) ed esempio di
applicazione ad una sequenza con fattore di interpolazione F=2.
Lo spettro della sequenza interpolata risultera':
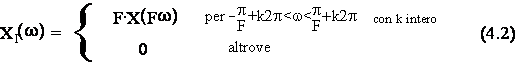
come illustra l'esempio di figura 4.2 nel caso F=2.
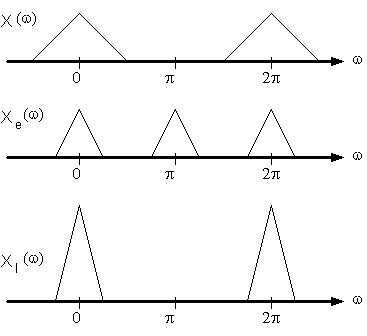
Fig. 4.2. Esempio di spettro di una sequenza prima dell'elaborazione (alto), dopo l'espansione (mezzo) e dopo il filtraggio passabasso che fornisce la sequenza interpolata (basso).
In realta', andrebbe precisato che quanto detto si riferisce al concetto di interpolazione passa-basso, motivata dalla supposizione che l'informazione analogica originaria risiedeva nella parte bassa dello spettro. Tuttavia, la proprieta' secondo cui non vi e' perdita di informazione nel sottocampionare un segnale di un fattore F e' assai piu' generale e vale se lo spettro e' non nullo in una banda F volte piu' stretta, ovunque tale banda si trovi (anche non alle basse frequenze).
In tal caso, il segnale puo' ugualmente essere ricostruito mediante un diverso tipo di interpolazione. Infatti, se l'informazione analogica era originariamente presente in altre bande, e' possibile definire un'interpolazione passa-alto o passa-banda in maniera del tutto duale. Lo schema numerico di interpolazione va quindi modificato sostituendo un filtro passa-alto o passa-banda ideale dopo l'espansore.
4.2 Esercizio.
Data una sequenza x(n), ottenuta da un campionamento con periodo T di un segnale analogico x(t), progettare un sistema di elaborazione numerico che fornisce, a partire dai campioni x(n), la sequenza ottenibile con un ipotetico campionamento del segnale x(t) con periodo T/2.
Svolgimento.
Si tratta di applicare lo schema esposto nel par. 4.1. Il sistema numerico di elaborazione operante su x(k) sara' costituito dalla cascata di un espansore di un fattore 2 e da un filtro passabasso ideale che elimina meta' banda ed amplifica (in frequenza) di due volte, cioe' la ripetizione spettrale della funzione:
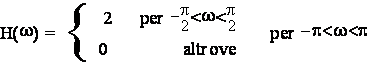
che ha una risposta impulsiva:

Come era ovvio, se si esamina il risultato della convoluzione del filtro h(n) con l'ingresso (i campioni espansi di x(n)), l'operazione cosi' progettata negli istanti pari lascia passare inalterati i campioni espansi di x(n), mentre in quelli dispari li interpola. Infatti h(n) vale 1 nell'origine e 0 negli altri istanti pari. Tale proprieta' puo' essere sfruttata per controllare la correttezza del progetto di h(n).
5. Decimazione.
5.1 Teoria.
L'operazione complementare all'espansione e' la decimazione. Essa consiste nel cancellare dalla sequenza su cui si opera un certo numero di campioni con cadenza periodica. In altre parole, data una determinata sequenza, si estrae, a partire dal campione nell'origine, un campione ogni F campioni della sequenza originaria, ove F e' detto fattore di decimazione. La sequenza decimata risulta percio' essere F volte piu' corta. Matematicamente si puo' scrivere la seguente relazione:
xd(n) = x(Fn) (5.1)
L'esempio grafico di fig. 5.1 illustra l'operazione.
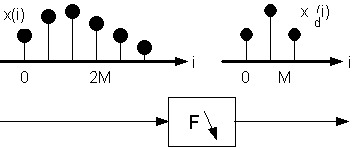
Fig. 5.1. Esempio di decimazione con fattore 2.
Lo spettro della sequenza decimata risulta attenuato in altezza del fattore F, espanso e replicato in modo da risultare comunque periodico di periodo 2p, cioe':
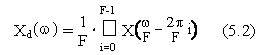
che graficamente corrisponde a quanto mostrato in fig. 5.2.
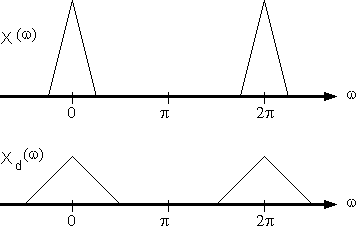
Fig. 5.2. Esempio di spettro di una sequenza decimata di un fattore 2 (in basso) in relazione a quello della sequenza originaria.
Ovviamente, se si desidera rappresentare correttamente un segnale campionato, e' necessario controllare che lo spettro della sequenza decimata non comporti sovrapposizioni spettrali (aliasing). Infatti, l'operazione di decimazione, come del resto anche il sottocampionamento analogico, non prevede alcun pre-filtraggio anti-aliasing.
In tal senso, la decimazione e' un'operazione "a rischio", poiche' non comporta perdite informative se e solo se lo spettro possiede in realta' una banda F volte piu' ristretta rispetto al dominio di Fourier originario. Come gia' detto a proposito della interpolazione, si noti anche qui come tale requisito non implichi una banda di tipo passa-basso, ma anche segnali con spettri di tipo passa-alto o passa-banda possono essere perfettamente ricostruiti.
5.2 Esercizio.
Data la sequenza x(n) avente uno spettro in w pari a X(w), calcolare analiticamente lo spettro Y(w) della sequenza y(n) ottenuta nel seguente modo:
y(n) = x(2n) - x(2n-1)
Svolgimento.
Si definisca, per comodita', la sequenza a(n):
a(n) = x(n) - x(n-1)
Lo spettro di a(n), cioe' A(w), risulta ovviamente:
A(w) = X(w) - e-jw X(w
Essendo poi:
y(n) = a(2n)
si ottiene, in base all'eq. (5.2):
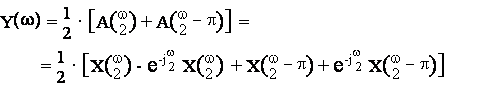
6. Uso della trasformata continua di Fourier.
6.1 Teoria.
La trasformata continua di Fourier X(w) di una sequenza x(n), che si estende da n=0 ad n=N-1, e' definita come:
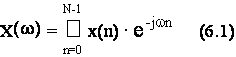
Ovviamente, se la sequenza x(n) e' definita in un generico intervallo [N , N ], anche l'indice n si estendera' da n=N ad n=N
La funzione X(w) e' comunemente detta spettro continuo della sequenza x(n) o, piu' semplicemente, spettro di x(n).
La trasformata inversa continua di Fourier consente di risalire alla sequenza originaria tramite la seguente relazione integrale:
![]()
Si noti che, mentre la sequenza e' una funzione della variabile discreta reale n, la trasformata continua di Fourier e' (come dice appunto il nome) una funzione complessa di variabile continua complessa (la pulsazione normalizzata w
Fra le proprieta' della trasformata continua di Fourier si ricordano le seguenti particolari relazioni:
dati F = X(w e F = Y(w allora
F = X*(w (6.3)
F = X(w Y(w (6.4)
F = F = X*(w Y(w) (6.5)
Le ultime due relazioni sono particolarmente utili poiche' consentono di calcolare la convoluzione e la correlazione fra due sequenze come prodotto nel dominio di Fourier delle rispettive trasformate, per poi antitrasformarne il risultato.
6.2 Esercizio.
Sia y(n) la sequenza ottenuta per differenziazione (ovvero y(n) = x(n)-x(n-1)) dalla sequenza x(n) caratterizzata dal seguente spettro, nella variabile complessa continua w
X(w) = 1 + cos w
Si chiede di calcolare lo spettro Y(w) della sequenza y(n), nonche' il suo spettro di densita' di energia.
Svolgimento.
Il filtro differenziatore ha per risposta impulsiva:
h(n) = d(n) - d(n-1)
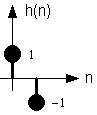
Fig. 6.1. Risposta impulsiva del filtro differenziatore.
La trasformata di Fourier continua H(w) di h(n) e':
H(w) = 1 - e-jw
Lo spettro Y(w) dell'uscita sara' dato da:
Y(w) = X(w) H(w) = [1 + cos w] [1 - e-jw
mentre lo spettro di densita' di energia di y(n) e':
Y*(w) Y(w) = X*(w) H*(w) X(w) H(w
= [1 + cos w [1 - ejw] [1 - e-jw] = [1 + cos w [2 - 2 cos w
7. Uso della trasformata discreta di Fourier.
7.1 Teoria.
La trasformata discreta di Fourier (Discrete Fourier Transform - DFT) di una sequenza x(n) di lunghezza N, e' una sequenza X(k), di lunghezza N, definita dalla:
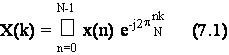
mentre la trasformata discreta inversa di Fourier (Inversa Discrete Fourier Transform - IDFT) di una sequenza X(k) di lunghezza N, e' una sequenza x(n), di lunghezza N, data da:
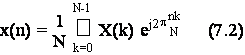
Definiti i vettori:
x = [ x(0) , x(1) , ... , x(N-1) ]T (7.3)
X = [ X(0) , X(1) , ... , X(N-1) ]T (7.4)
e le matrici simmetriche A e B di dimensione NxN, i cui elementi e , con 0 n N-1 (indice di riga) e 0 k N-1 (indice di colonna), sono:
(7.5)
= = / N (7.6)
le trasformazioni (7.1) e (7.2) possono alternativamente essere espresse mediante gli operatori lineari A e B=A come:
X = A x (7.7)
x = A X = B X (7.8)
Poiche' i vettori componenti la matrici A/![]() e B
e B ![]() sono ortogonali e di modulo
unitario, gli operatori corrispondenti sono delle semplici rotazioni di
coordinate e valgono percio' le proprieta' geometriche delle trasformazioni
ortonormali (ad esempio, conservazione delle distanze).
sono ortogonali e di modulo
unitario, gli operatori corrispondenti sono delle semplici rotazioni di
coordinate e valgono percio' le proprieta' geometriche delle trasformazioni
ortonormali (ad esempio, conservazione delle distanze).
La trasformata discreta di Fourier e' utilizzata in molte applicazioni di base dell'elaborazione numerica dei segnali, quali calcolo di correlazioni e convoluzioni circolari, filtraggi e stime spettrali. La popolarita' risiede nel fatto che tali operazioni sono immediate nel dominio trasformato discreto di Fourier e nel fatto che esistono algoritmi di calcolo rapido della DFT (la trasformata discreta veloce di Fourier - Fast Fourier Transform - FFT), facilmente implementabili su un processore numerico, talvolta addirittura integrati su componenti elettronici appositi.
7.2 Esercizio (filtraggio mediante sovrapposizione ed estrazione).
Data la sequenza a tempo discreto x(n) di fig. 7.1 in ingresso al filtro differenziatore, con risposta impulsiva h(n) di fig. 7.2, calcolarne l'uscita y(n)=x(n) h(n) mediante l'uso della DFT su 4 punti con il metodo di sovrapposizione ed estrazione.
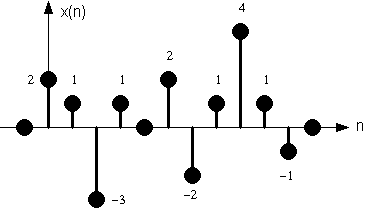
Fig. 7.1. Sequenza di ingresso al filtro.

Fig. 7.2. Risposta impulsiva del filtro differenziatore.
Soluzione.
Dovendo utilizzare DFT su 4 punti, si calcolano in primo luogo le matrici A e B definite dalle (7.5) e (7.6):

la DFT di h(n) risulta quindi:

Come richiesto dal testo dell'esercizio, calcoliamo le convoluzioni utilizzando la DFT, dopo aver aggiunto uno zero in testa alla sequenza x(n) per evitare errori di circolarita'. La procedura grafica diretta (qui sicuramente la piu' semplice ed immediata) potra' essere utilizzata per controllare a posteriori i risultati ottenuti. La procedura di soluzione e' la seguente:
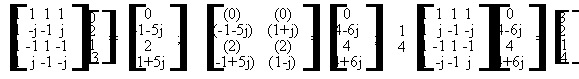
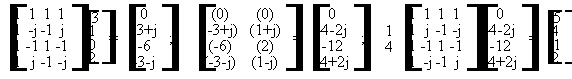
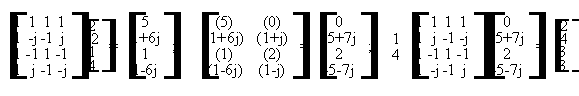
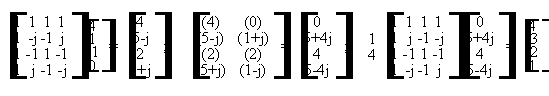
A questo punto, basta ignorare il primo elemento di ogni vettore (uno solo poiche' h(n) ha lunghezza 2), che e' affetto da errori di circolarita' durante l'operazione di convoluzione circolare mediante l'uso di algoritmi DFT, dovuti all'influenza ciclica dell'ultimo elemento del vettore della sequenza sul primo elemento del vettore risultante; quindi, "incollare" consecutivamente gli elementi restanti. Il risultato finale e':
y(n) = 2 -1 -4 4 -1 2 -4 3 3 -3 -2 1
che e' mostrato nella fig. 7.3.
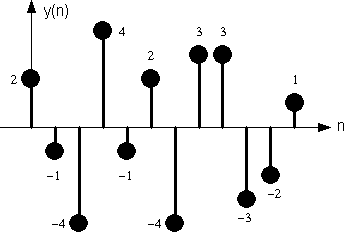
Fig. 7.3. Sequenza risultante dal filtraggio.
7.3 Esercizio (filtraggio mediante sovrapposizione e somma).
Data la sequenza a tempo discreto x(n) di fig. 7.1 in ingresso al filtro differenziatore, con risposta impulsiva h(n) di fig. 7.2, calcolarne l'uscita y(n)=x(n) h(n) mediante l'uso della DFT su 4 punti con il metodo di sovrapposizione e somma.
Soluzione.
Si tratta dello stesso esercizio 7.2 da risolvere con il metodo di sovrapposizione e somma mediante l'uso della DFT. Le matrici di trasformazione di Fourier A e B ed il vettore H rappresentante il filtro sono gli stessi dell'esercizio precedente. E' necessario utilizzare uno zero in coda ad ogni vettore da trasformare per evitare errori di circolarita' (un solo zero perche' h(n) ha lunghezza 2). Il calcolo va effettuato come segue:
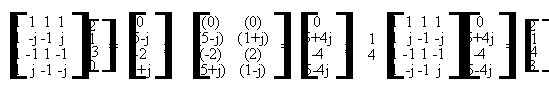
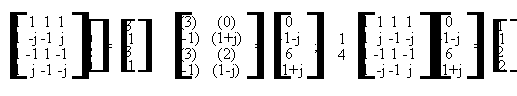
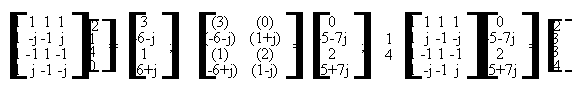
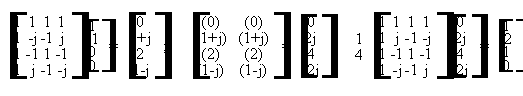
Per ottenere il risultato finale, poiche' la convoluzione mediante DFT e' circolare, i risultati ottenuti vanno considerati consecutivamente, effettuando la somma fra ogni ultimo elemento dei vettori ed il primo elemento del successivo vettore (esenti da errori di circolarita' per lo zero inserito in coda ai vettori da trasformare), ottenendo:
y(n) = 2 -1 -4 (3+1) -1 2 (-2-2) 3 3 (-4+1) -2 1 0
ottenendo il medesimo risultato illustato nella fig. 7.3.

Fig. 7.3. Sequenza risultante dal filtraggio.
Risulta evidente come sia preferibile dal punto di vista computazionale il metodo di sovrapposizione ed estrazione poiche' non prevede alcuna operazione aritmetica di addizione fra risultati della DFT.
Parte II. La trasformata Z.
8. Equazioni lineari alle differenze.
8.1 Richiamo teorico.
Una sotto-classe di sistemi lineari invarianti alla traslazione e' quella in cui la sequenza di ingresso x(n) e quella di uscita y(n) sono legate da un'equazione alle differenze lineare a coefficienti costanti di ordine N:
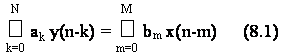
La sequenza della risposta impulsiva di un sistema h(n), ovvero l'uscita y(n) quando in ingresso e' presente un impulso unitario d(n), serve a caratterizzare il comportamento del sistema stesso. Tuttavia, per un sistema del tipo (8.1) la risposta impulsiva non e' univocamente definita. Infatti, la soluzione dell'eq. (8.1) non e' unica, ma esistono 2N possibili soluzioni.
La soluzione puo' divenire unica solo imponendo vincoli alla h(n) quali la causalita' oppure l'anticausalita' od anche, in alternativa, la stabilita' del sistema. La soluzione causale impone l'uscita sia nulla per istanti negativi, quella anticausale che lo sia per istanti positivi o nulli; quella stabile che la risposta impulsiva del sistema converga asintoticamente a zero (stabilita' asintotica) oppure sia limitatata entro valori finiti (stabilita' marginale o, piu' semplicemente, stabilita') al tendere all'infinito della variabile tempo-discreto.
Dal punto di vista sperimentale, un criterio di stabilita' spesso usato si basa sul comportamento ingresso/uscita del sistema. In particolare, e' un sistema stabile risponde ad un qualunque ingresso limitato con un'uscita anch'essa limitata (criterio BIBO - Bounded Input Bounded Output).
8.2 Esempio.
Sia dato, a titolo di esempio, il sistema del primo ordine:
y(n) = a y(n-1) + x(n) (8.2)
ove a e' una costante arbitraria.
Esistono due soluzioni della (8.2): una causale e l'altra anticausale. Per ottenere la sequenza della risposta impulsiva h(n) nel caso causale, si imponga x(n)=d(n) e si osservi l'uscita y(n), supponendo condizioni iniziali di riposo, cioe' y(n)=h(n)=0 per n<0.
Iterando l'eq. (8.2) si ottiene:
y(n) = h(n) = 0 per n<0
y(0) = h(0) = a y(-1) +1 = 1
y(1) = h(1) = a y(0) = a
y(2) = h(2) = a y(1) = a
y(n) = h(n) = a y(n-1) = an
Pertanto:
h(n) = an U(n) (8.3)
ove
![]()
Al contrario, se si cerca la soluzione anticausale si impone sempre x(n)=d(n), ma si assuma y(n)=h(n)=0 per n>0, e si osserva l'uscita y(n).
L'equazione alle differenze (8.2) puo' essere riscritta, per comodita', come segue:
y(n) = a y(n+1) - a x(n+1) (8.4)
Si ha allora, iterando la (8.4):
y(n) = h(n) = 0 per n>0
y(0) = h(0) = a y(1) = 0
y(-1) = h(-1) = a y(0) - a = - a
y(-2) = h(-2) = a y(-1) = - a
y(n) = h(n) = a y(n+1) = - an
Quindi:
h(n) = - an U(-n-1) (8.5)
In realta', e' solitamente di interesse applicativo cercare la soluzione stabile del sistema. Nel caso del sistema del primo ordine (8.2), la soluzione stabile coincide con quella causale (8.3) se |a|<1 (e' una soluzione asintoticamente stabile), e' quella anticausale (8.5) se |a|>1 (e' una soluzione asintoticamente stabile), mentre sono entrambe stabili (marginalmente) le soluzioni (sia la causale (8.3) che la anticausale (8.5)) se |a|=1.
Piu' in generale, dato un sistema di ordine generico come quello dell'eq. (8.1), la ricerca della sua soluzione stabile puo' portare a determinare contemporaneamente una parte causale ed una parte anticausale. Infatti, come risultera' ancor piu' evidente nel seguito, eseguendo una decomposizione del sistema in sottosistemi paralleli equivalenti con il vincolo della stabilita', alcuni sottosistemi risulteranno essere causali, mentre gli altri saranno anticausali.
9. Alcune trasformate-Z notevoli.
9.1 Teoria.
Data una sequenza x(k) che si estende da k=0 a k=N-1, si definisce trasformata-Z di x(k) la seguente funzione della variabile complessa z:
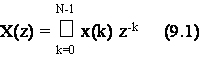
Ovviamente, la definizione (monolatera) della trasformata-Z data dalla (9.1) puo' essere facilmente generalizzata per intervalli di definizione della x(k) qualunque, facendo variare l'indice k fra k=N e k=N anche negativi (trasformata bilatera) o persino di valore infinito (sempre che la somma risulti finita).
In ogni caso, la convergenza della (9.1) dipende in generale dai valori assunti dalla variabile complessa z. Pertanto, si definira' un opportuno raggio di convergenza della trasformazione.
Una proprieta' molto importante nello svolgimento analitico degli esercizi di calcolo della trasformata-Z e' la somma:
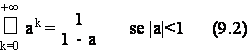
ove a e' un numero complesso ed R= e' la regione di convergenza della serie ak
9.2 Esercizio (gradino unitario).
Data la sequenza:
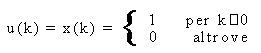
determinarne la trasformata-Z.
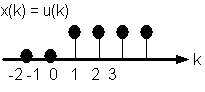
Fig. 9.1. La sequenza "gradino unitario".
Svolgimento.
Dalla definizione (9.1) si ha:
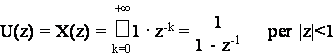
in base alla proprieta' (9.2).
9.3 Esercizio (gradino unitario traslato).
Data la sequenza:
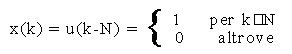
determinarne la trasformata-Z.
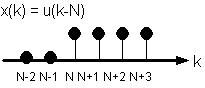
Fig. 9.2. La sequenza "gradino unitario traslato".
Svolgimento.
Dalla definizione (9.1) e ponendo m=k-N si ottiene:
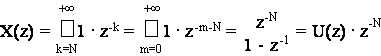
Si noti come un ritardo di N campioni comporti un fattore moltiplicativo pari a z-N nella trasformata-Z. Detta proprieta' della trasformata-Z sussiste in generale per qualunque traslazione di N passi di campionamento in anticipo ( zN) o in ritardo ( z-N
9.4 Esercizio (rettangolo unitario).
Data la sequenza:
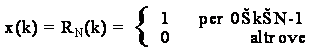
determinarne la trasformata-Z.
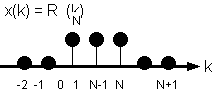
Fig. 9.3. La sequenza "rettangolo unitario".
Svolgimento.
Osservando che:
x(k) = RN(k) = u(k) - u(k-N)
si ottiene, per la linearita' dell'operatore "Z":
![]()
ove sono stati utilizzati i risultati per le funzioni a gradino precedentemente calcolati.
9.5 Esercizio (rampa finita).
Data la sequenza:
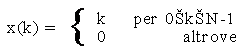
determinarne la trasformata-Z.
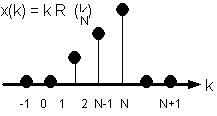
Fig. 9.4. La sequenza "rampa finita".
Svolgimento.
Essendo (proprieta' di derivazione in z):
![]()
dalla definizione (9.1) e ricordando il risultato per il rettangolo unitario si ottiene:
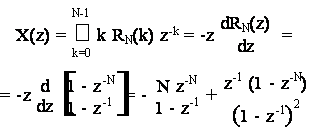
9.6 Esercizio (esponenziale causale).
Data la sequenza:
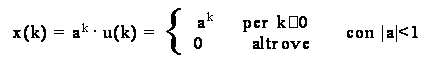
determinarne la trasformata-Z.
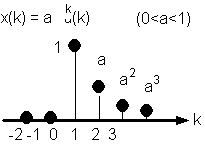
Fig. 9.5. La sequenza "esponenziale causale".
Svolgimento.
Dalla definizione (9.1) e per la proprieta' (9.2) si ottiene:
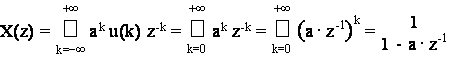
La regione di convergenza della serie e':
R
9.7 Esercizio (esponenziale anticausale).
Data la sequenza:
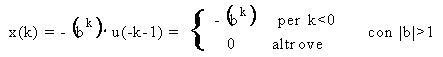
determinarne la trasformata-Z.
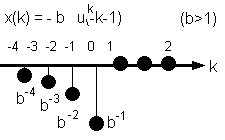
Fig. 9.6. La sequenza "esponenziale anticausale".
Svolgimento.
Dalla definizione (9.1) e per la proprieta' (9.2) si ottiene, ponendo per comodita' m=-k:
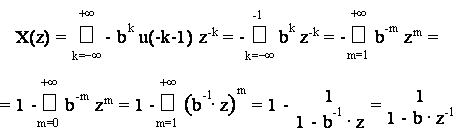
Il risultato e' formalmente identico a quello della serie calcolata nel precedente esercizio, ma la regione di convergenza e', in questo caso, quella complementare, cioe':
R
10. Metodo dei residui.
10.1 Teorema dei residui.
Sia V(x) un rapporto di polinomi nella variabile complessa x:
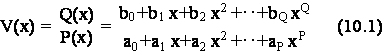
Se il quoziente non e' proprio, ovvero se Q P, cioe' se il grado del numeratore e' maggiore o uguale a quello del denominatore, lo si rende proprio effettuando la divisione tra polinomi con resto, ottenendo cosi':
![]()
ove H(x) e' un rapporto di polinomi dato da:
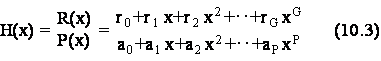
in cui R(x) e' il resto della divisione costituito da un polinomio di grado G<P, con cio' ottenendo un quoziente proprio di polinomi in x, in cui il grado del numeratore e' strettamente minore del grado del denominatore.
Nel caso di quoziente proprio (Q<P), ovvero se il grado del numeratore e' gia' minore di quello del denominatore, non si effettua alcuna divisione e si impone R(x)=Q(x) (quindi anche H(x)=V(x), ri=bi e G=Q) in tutta la procedura esposta nel seguito.
Il teorema dei residui afferma che e' possibile espandere in fratti semplici un quoziente proprio di polinomi nel modo seguente:
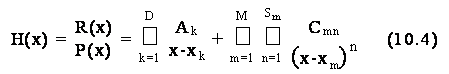
ove il polinomio P(x) ha P zeri (quindi V(x) ed H(x) hanno P poli) di cui D distinti (xk) ed M multipli (xm) con molteplicita' S , S , ..., SM, rispettivamente, con:
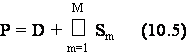
mentre Ak e Cmn sono i residui definiti dalle espressioni:
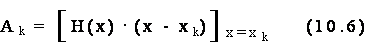
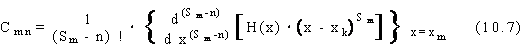
Per utilizzare per il calcolo di antitrasformate-Z l'espansione in fratti semplici, teste' illustrata in funzione di una generica variabile complessa x, e' possibile considerare l'espressione nel dominio trasformato come un rapporto di polinomi nella variabile complessa z o, alternativamente, nella variabile complessa z . Entrambe le vie risultano in generale proponibili. Tuttavia, al fine di poter applicare direttamente le regole di antitrasformazione gia' note ai diversi fratti semplici ottenibili con il metodo dei residui, e' sovente consigliabile operare nella variabile complessa z
10.2 Esercizio (poli distinti).
Data l'equazione lineare alle differenze:
y(n) = 2.4 y(n-1) - 0.8 y(n-2) + x(n) + 1.2 x(n-2)
calcolare analiticamente la funzione di trasferimento in z e la risposta impulsiva corrispondente alla soluzione permanente stabile.
Svolgimento.
Dato che l'operatore z rappresenta il ritardo di un passo di campionamento, l'equazione alle differenze puo' essere riscritta nel dominio z come segue:
Y(z) = 2.4 z Y(z) - 0.8 z Y(z) + X(z) + 1.2 z X(z)
da cui si ottiene la funzione di trasferimento H(z):
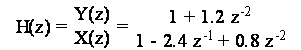
Per calcolare analiticamente la risposta impulsiva, occorre scomporre in fratti semplici la precedente espressione ed antitrasformare. Poiche' il grado del numeratore e' uguale a quello del denominatore, va effettuata la divisione tra i due polinomi nella maniera seguente:
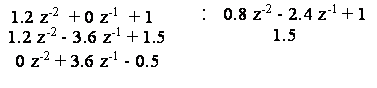
cioe':
![]()
Si noti come la divisione vada effettuata soltanto dopo aver riordinato i polinomi in base alle potenze di z , in modo da abbassare di grado il resto (z risulta infatti moltiplicato per 0).
Essendo H'(z) una frazione propria, e' adesso possibile applicare il teorema dei residui. Quindi, si calcolano le radici del denominatore (i poli del sistema) che risultano essere pari a 2 e 0.4. Pertanto, si puo' scrivere che:
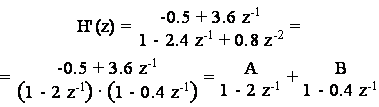
ove i residui A e B risultano, per definizione:
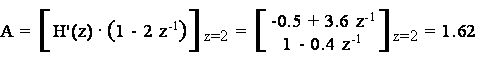
![]()
quindi, raccogliendo i termini:
![]()
che, antitrasformato, fornisce la seguente soluzione:
h(n) = 1.5 d(n) - 1.62 (2)n u(-n-1) - 2.12 (0.4)n u(n)
Si osservi dall'espressione analitica e dal grafico di fig. 10.1 come la soluzione h(n) stabile contenga un impulso nell'origine, una parte anticausale ed una causale.
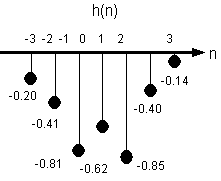
Fig. 10.1. La risposta impulsiva h(n).
La procedura ora illustrata e' del tutto generale e si applica anche a sistemi con poli complessi. In tal caso, il calcolo dovra' essere condotto in forma complessa per ciascun polo. Tuttavia, se il sistema e' reale, la risposta impulsiva complessiva sara' sempre reale, trattandosi dell'uscita di un sistema reale con ingresso d(n) reale. Di questa proprieta' ci si puo' avvalere per semplificare analiticamente il risultato ottenuto, controllando nel contempo la correttezza dello stesso.
10.3 Esercizio (poli multipli).
Calcolare la risposta impulsiva corrispondente alla soluzione permanente e stabile del sistema lineare avente la seguente funzione di trasferimento:
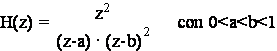
Svolgimento.
Riscriviamo, per comodita', la H(z) nel seguente modo:
![]()
Poiche' la F(z) e' una frazione propria, ad essa e' applicabile il teorema dei residui nella variabile complessa z. Pertanto imponiamo che:
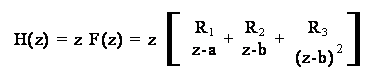
che sappiamo (avendo "furbamente" lasciato un fattore z a moltiplicare tutti i fratti semplici espressi in z) essere la trasformata-Z di:
h(n) = R (a)n + R (b)n + R n (b)n-1 u(n)
I residui R , R R si ottengono come:
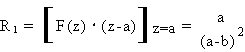
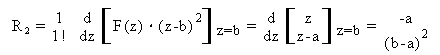
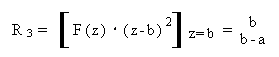
Pertanto, la risposta impulsiva h(n) e':

Si osservi dall'espressione analitica e dal
grafico di fig. 10.2 come h(n) sia una sequenza causale stabile. La
presenza
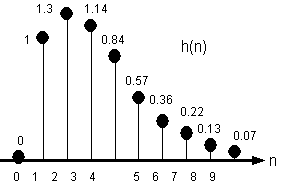
Fig. 10.2. La risposta impulsiva h(n) per a=0.3 e b=0.5.
E' utile osservare
come la tecnica qui utilizzata di esprimere H(z) come [z F(z)] si riveli particolarmente
indicata per applicare il teorema dei residui nella variabile z, anziche' in z , per potere
cosi' decomporre in fratti semplici l'espressione da antitrasformare.
Ovviamente, e' la funzione F(z) che deve in questo caso godere dei requisiti di
applicabilita'
10.4 Esercizio (sequenze di autocorrelazione).
Dato il sistema lineare con funzione di trasferimento in z:
![]()
calcolare la sequenza di autocorrelazione all'uscita
Svolgimento.
Lo spettro di
Cyy(k) = Cxx(k) h(-k) h(k) = d(k) h(-k) h(k) =
= h(-k) h(k) = Chh(k)
Il calcolo temporale
di Chh(k), consigliabile nel
caso di sistemi a soli zeri (sistemi MA),
e' qui complicato (e quindi poco indicato) a causa della durata infinita di
h(n) dovuta alla presenza di poli (oltre agli zeri) nella funzione di
trasferimento
La trasformata della sequenza di autocorrelazione dell'uscita sara' data da:
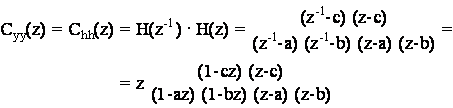
ove il fattore z e' stato messo in evidenza per una piu' agevole antitrasformazione (vedi esercizio 10.3).
Il fatto che Cyy(z) sia una frazione propria di
polinomi in z consente inoltre l'espansione in fratti semplici della parte
rimanente mediante il teorema dei residui. I poli
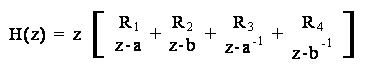
Tuttavia, ricordando che ogni sequenza di autocorrelazione gode della proprieta' di simmetria coniugata, e' sufficiente calcolarne analiticamente soltanto i valori nell'origine e per istanti k positivi, per poi ribaltarli e coniugarli per k negativi. In particolare, dato che per le caratteristiche di simmetria tale sequenza dovra' essere composta da una parte causale (k 0) ed una anticausale (k<0), sara' sufficiente valutare la prima per calcolare l'intera risposta.
Esaminando il rapporto di polinomi in z ottenuto in questo caso, e' possibile valutare i due soli residui R ed R . Percio', essendo:
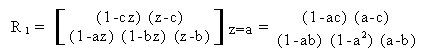
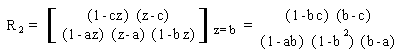
e' conveniente antitrasformare la sola parte causale:
Cyy(k) = Chh(k) = R (a)k + R (b)k u(k) per k 0
Da cui, estendendola per k<0 si ottiene il risultato finale:
Cyy(k) = Chh(k) = R (a)|k| + R (b)|k|
illustrato graficamente dalla fig. 10.3.
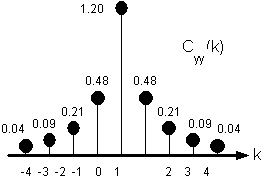
Fig. 10.3. La sequenza di autocorrelazione Cyy(k) calcolata per a=0.3, b=0.5 e c=0.4.
Si osservi inoltre come la procedura semplificata ora illustrata si sarebbe potuta applicare anche in presenza di frazioni non proprie nella espressione della trasformata-Z da antitrasformare. In tal caso, basta effettuare la divisione tra polinomi in z, applicando successivamente il teorema dei residui semplificato all'espessione ottenuta. Infatti, e' possibile individuare una parte causale ed una anticausale non solo nel resto (che e' una frazione propria), ma anche nel quoziente, che e' composto da potenze di z (parte anticausale) oppure di z e numeri puri (parte causale).
Parte III. Filtri numerici.
11. Grafi di sistema.
11.1 Premessa.
In questo capitolo ci
occuperemo della rappresentazione di sistemi a tempo discreto mediante grafi. Un grafo di flusso e' una rete di
rami orientati che si connettono in corrispondenza di nodi. Ad ogni nodo e' associata una variabile o valore
Il concetto di grafo
e' percio' legato a quello di rete. Tuttavia, e' necessario sottolineare che un
grafo e' una realizzazione
dell'algoritmo matematico di elaborazione, ovvero un modello che possiede la funzione di trasferimento desiderato,
mentre una rete e' lo schema circuitale che implementa l'algoritmo stesso e che
quindi potrebbe venir utilizzata come schema elettronico
11.2 Esercizio (realizzazione in forma canonica).
Determinare la funzione
di trasferimento
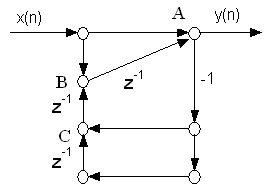
Fig. 11.1. Esempio di grafo di sistema.
Svolgimento.
Detti A, B e C i nodi
evidenziati in fig. 11.1, e' possibile scrivere le seguenti equazioni in
funzione dei valori
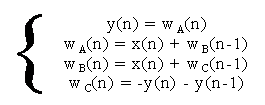
Per risolvere il sistema in forma ricorsiva occorre esprimere l'uscita y(i) in funzione dell'ingresso x(j), agli istanti i=n,n-1,..; e j=n,n-1,... Sostituendo progressivamente si ottiene:
wB(n) = x(n) - y(n-1) - y(n-2)
wA(n) = x(n) + x(n-1) - y(n-2) - y(n-3)
y(n) = x(n) + x(n-1) - y(n-2) - y(n-3)
y(n) + y(n-2) + y(n-3) = x(n) + x(n-1)
che rappresenta l'equazione alle differenze
Y(z) 1 + z + z = X(z) 1 + z
ottenendo quindi la seguente funzione di trasferimento:
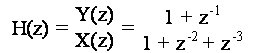
la cui forma canonica e' data dal grafo di fig. 11.2.
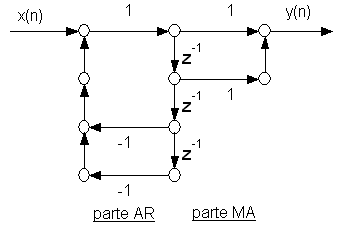
Fig. 11.2.
Realizzazione in forma canonica
Si noti come la
struttura in forma canonica sia costituita dalla cascata di un blocco a soli
poli (parte AR) ed uno a soli zeri
(parte MA), separati da una pila di
fattori ritardo z
(in quantita' pari all'ordine
11.3 Esercizio (sistema a traliccio).
Si consideri il
sistema interconnesso rappresentato dal grafo a traliccio di fig. 11.3, avente
un ingresso e due uscite. Determinare la matrice di trasferimento (cioe' le due
funzioni di trasferimento) in z
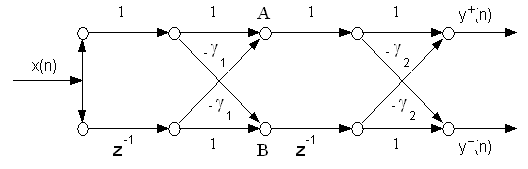
|g |<1 e |g |<1
Fig. 11.3. Grafo di un sistema interconnesso a traliccio.
Svolgimento.
La soluzione
Scriviamo le equazioni risolventi direttamente nel dominio z. Ai nodi A e B si ottiene:
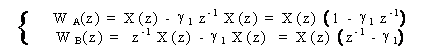
mentre le equazioni di equilibrio alle uscite y (n) ed y (n) sono:
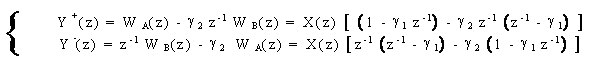
Pertanto, la matrice di trasferimento H(z) diviene:

Si puo' notare che H (z) ed H (z) sono due sistemi a soli zeri (sistemi MA) con funzione di trasferimento reciprocamente speculare. Da qui deriva per i coefficienti g e g il nome di "coefficienti di riflessione".
Inoltre, gli zeri di H (z) sono esattamente quelli di H (z) invertiti rispetto al cerchio
unitario. Per cui, se H (z) ha
tutti gli zeri entro il cerchio di raggio unitario (condizione che definisce un
filtro a fase minima), allora H (z) li ha tutti fuori
12. Filtri a fase minima.
12.1 Teoria.
E' possibile dimostrare che, nella classe delle sequenze causali , con 1 i I, con ugual modulo della risposta in frequenza |Hi(ejw)|=|H(ejw)|, detta Ei(M) l'energia della sequenza hi(n) compresa tra l'origine dei tempi e l'istante M, ovvero la quantita':
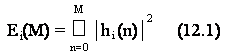
risulta che Ei(M) e' massima per un certo i=k se e solo se hk(n) e' una sequenza a fase minima.
Pertanto la condizione di fase minima fornisce un utile criterio per progettare filtri numerici con una data risposta in frequenza in modulo e con il minimo ritardo (dell'energia) della risposta impulsiva; in altre parole, filtri la cui risposta e' la piu' "corta" possibile.
Un filtro a fase
minima possiede i propri poli e zeri entro il cerchio di raggio unitario. La
procedura per rendere a fase minima
un filtro che non lo e', mantenendone il modulo della risposta in frequenza, richiede
la sostituzione degli zeri e dei poli esterni al cerchio unitario con i
reciproci coniugati all'interno
Dal punto di vista formale, la sostituzione degli zeri (o poli) esterni con i reciproci coniugati corrisponde a moltiplicare la funzione di trasferimento H(z) per un filtro passatutto in base alla relazione seguente:
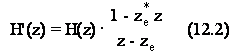
ove ze e' un generico zero esterno al cerchio unitario. Analoga (reciproca) operazione e' richiesta per i poli.
Piu' in generale, e' opportuno osservare che se il filtro e' reale e se vi sono zeri (poli) complessi con parte immaginaria non nulla, devono allora necessariamente esistere altri zeri (poli) coniugati dei precedenti.
12.2 Esercizio.
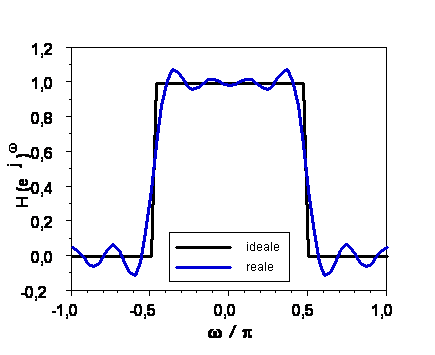
Un filtro numerico e' caratterizzato dalla seguente risposta in frequenza:
H(ejw) = 1 - 0.5 cos w
Determinare la risposta
|G(ejw)| = |H(ejw)| per ogni w.
Svolgimento.
Essendo nota la particolare relazione seguente tra la trasformata di Fourier e quella Z:
d(n-1) + d(n+1) = F [2 cos w] = Z [z + z]
e' possibile ricavare immediatamente la H(z):
![]()
Occorre adesso calcolare gli zeri di H(z) per verificare la condizione di fase minima. Posto, per comodita', y = (z + z), si ottiene:
![]()
Risostituendo la variabile z si ottiene (per z finito):
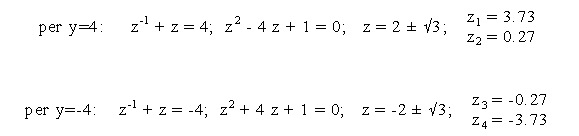
Pertanto la funzione di trasferimento H(z) risulta:
H(z) = (-1/16) z z - z z - z z - z z - z =
= (-1/16) z z - 3.37 z - 0.27 z + 0.27 z + 3.37
Il sistema presenta due zeri entro il cerchio di raggio unitario e due zeri fuori dal cerchio unitario. Quindi non rappresenta un sistema a fase minima.
Per imporre la
condizione di fase minima occorre sostituire in H(z) i termini relativi agli
zeri esterni al cerchio unitario con altri termini in cui gli zeri siano ribaltati
specularmente all'interno
G(z) = (-1/16) z 1 - z z * z - z z - z 1 - z z * =
= (-1/16) z 1 - 3.37 z z - 0.27 z + 0.27 1 + 3.37 z
che e' la funzione di trasferimento desiderata.
13. Progetto mediante la trasformata inversa di Fourier.
13.1 Teoria.
Occorre innanzitutto precisare che, talvolta, riferendosi alle risposte in frequenza, vengono utilizzate notazioni difformi: infatti, mentre la notazione H(w) si riferisce alla trasformata di Fourier della sequenza h(n), con H(ejw) si suole intendere la trasformata-Z H(z) della sequenza h(n) valutata in z=ejw. Semplicemente confrontando le definizioni della trasformata-Z e di quella di Fourier, si deduce che le due funzioni di w sono coincidenti per ogni w.
Data una risposta in
frequenza H(w), funzione periodica
di periodo 2p della variabile continua
w, e' possibile risalire alla risposta
impulsiva h(n)
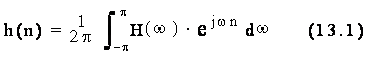
Ove possibile, si effettua l'operazione di antitrasformazione per via analitica. Altrimenti, possono essere usate procedure numeriche per calcolare l'integrale definito espresso dalla (13.1).
Fra queste ultime, e'
possibile campionare la risposta in frequenza continua H(w) ed antitrasformare utilizzando la IDFT (Trasformata discreta di Fourier
inversa). Questa operazione e' pero' teoricamente corretta solo se la H(w) risulta campionabile con il passo
prescelto, dipendente dalla durata della risposta impulsiva, come e' richiesto
dal (duale
La sequenza h(n) e',
in generale, di lunghezza infinita. Per questo motivo essa viene normalmente
troncata utilizzando opportune funzioni "finestra". Fra le caratteristiche delle numerose finestre proposte in letteratura, basti
qui ricordare che l'estrazione di campioni della h(n) deve essere tale da poter
assumere trascurabile il contributo
dei campioni non considerati. In pratica, il criterio e' quello di trascurare
le code della sequenza della risposta impulsiva laddove tutti gli ulteriori
campioni sono minori, in modulo, di una certa prefissata entita' (ad esempio:
il 10%
13.2 Esercizio (filtro derivatore).
Data la risposta in frequenza H(w), periodica di periodo 2p, che nell'intervallo frequenziale [-p , p] assume la forma:

calcolare la sequenza h(n) che ammette la H(w) come trasformata di Fourier e progettare un filtro numerico FIR che approssimi la stessa risposta in frequenza.
Svolgimento.
La funzione data
simula il comportamento di un derivatore entro la banda [-p , p].
In altre parole, se un segnale continuo fosse campionato correttamente (cioe'
senza produrre aliasing spettrale) e
fosse posto in ingresso al sistema, in uscita sarebbero presenti i campioni
della derivata temporale
Calcoliamo la antitrasformata in base alla (13.1):
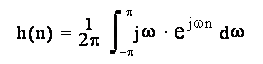
Per semplificare i calcoli, conviene valutare separatamente l'antitrasformata per n=0 e per n 0. Nel caso n=0 si ha, essendo l'integrale definito simmetricamente di una funzione dispari:
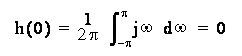
Nel caso n 0, integrando per parti si ottiene:

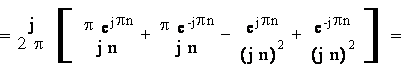
![]()
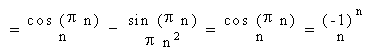
Il filtro FIR "derivatore numerico" puo' essere semplicemente realizzato estraendo simmetricamente da h(n) un numero di campioni consecutivi, centrati nell'origine in modo da massimizzare l'energia della risposta impulsiva (estrazione con finestra rettangolare).
Ovviamente, la bonta' della approssimazione dipendera' dal numero di campioni considerati. Se, ad esempio, si sceglie di tralasciare i campioni che posseggono un'energia inferiore ad 1/100 di quella massima, si ottiene un filtro di lunghezza 21 la cui trasformata-Z risulta:
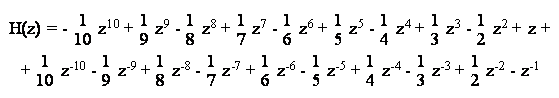
I campioni cosi' estratti potranno essere moltiplicati per ulteriori funzioni finestra, qualora si desideri utilizzare finestre non uniformi. Si noti come, in ogni caso, l'estrazione simmetrica dei campioni comporti un filtro realizzato con componenti sia causale che anticausale.
13.3 Esercizio (filtro di Hilbert).
Data la risposta in frequenza H(w), periodica di periodo 2p, che nell'intervallo frequenziale [-p , p] assume la forma:
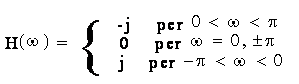
calcolare la sequenza h(n) che ammette la H(w) come trasformata di Fourier e progettare un filtro numerico FIR che approssimi la stessa risposta in frequenza.
Svolgimento.
La funzione data simula il comportamento di un filtro di Hilbert entro la banda [-p , p]. In altre parole, se un segnale continuo fosse campionato correttamente (cioe' senza produrre aliasing spettrale) e fosse posto in ingresso al sistema, in uscita sarebbero presenti i campioni della trasformata di Hilbert del segnale continuo di ingresso.
Calcoliamo la antitrasformata in base alla (13.1):
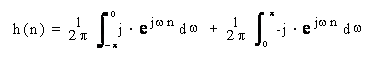
Per semplificare i calcoli, conviene valutare separatamente l'antitrasformata per n=0 e per n 0. Nel caso n=0 si ha, essendo l'integrale definito simmetricamente di una funzione dispari:
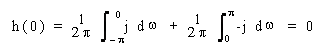
Nel caso n 0, integrando per parti si ottiene (dato che risulta ejp e-jp -1):
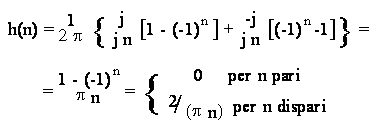
Il filtro FIR di Hilbert puo' essere semplicemente
realizzato estraendo simmetricamente da h(n) un numero di campioni consecutivi,
in maniera
14. Progetto mediante l'invarianza all'impulso.
14.1 Teoria.
Il metodo
dell'invarianza della risposta impulsiva (piu' brevemente: all'impulso)
consente di progettare un filtro numerico sfruttando un precedente progetto di
un corrispondente filtro analogico. I due filtri, in questo caso, conserveranno
la medesima risposta impulsiva nel senso che quella
Evidentemente, la
procedura richiede che la risposta impulsiva sia campionabile senza perdita di
rappresentazione in base al criterio di Nyquist. In caso contrario, sorge il
problema dell'aliasing spettrale
della risposta in frequenza
Per ottenere
l'invarianza della risposta impulsiva la procedura richiede la decomposizione
della stessa in fratti semplici. Operativamente, e' quasi obbligata la strada
della decomposizione mediante il teorema dei residui. In tal modo la somma di
fratti semplici nella variabile complessa analogica s e' facilmente
convertibile nella somma di corrispondenti fratti semplici nella variabile
complessa
![]()
ove c e' il polo "analogico" e T e' il periodo di campionamento.
14.2 Esercizio (poli complessi coniugati).
Dato il sistema
analogico
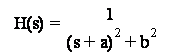
progettare con il metodo dell'invarianza impulsiva il filtro numerico che ne simula il comportamento.
Svolgimento.
Osservando il
denominatore di H(s) si nota immediatamente che, in quanto somma di quadrati,
questo deve presentare radici (poli
- a + j b e - a - j b
Dato che il grado
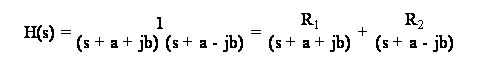
ove
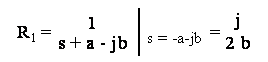
ed
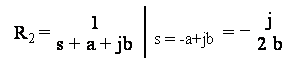
Data la (14.1), si ottiene per il filtro numerico la seguente funzione di trasferimento in z:


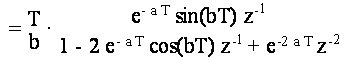
che corrisponde alla seguente equazione alle differenze:
y(n) = 2 e-a T cos(bT) y(n-1) -
- e-2 a T y(n-2) + (T/b) e- a T sin(bT) x(n-1)
L'espressione teste'
ricavata risulta utile nel caso, piuttosto comune, di sistemi numerici a
coefficienti reali. Infatti, puo' applicarsi come elemento di base per
sviluppare funzioni di trasferimento in s in fratti
14.3 Esercizio (filtro di Butterworth).
Progettare un filtro numerico con il metodo dell'invarianza all'impulso con le seguenti specifiche:
-) risposta in continua H(0) = 0 dB
-) modulo della risposta in frequenza tale che:
0 dB |H(f)|dB -3 dB per 0 |f| f (banda passante)
monotona decrescente per f |f| f (banda di transizione)
|H(f)|dB -10 dB per |f| f (banda oscura)
-) f = 1 KHz
-) f = 2 KHz
-) frequenza di campionamento fc = 10 KHz
Svolgimento.
Le specifiche richieste sono soddisfatte dalla classe dei filtri analogici di Butterworth, definita dalla seguente funzione di trasferimento a soli poli di ordine N nella variabile complessa di Laplace "s":
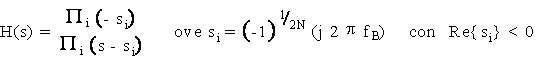
Dato che, sull'asse immaginario:

ove fB
e' la frequenza per cui |H(f)| =0.5 (corrispondente a -3 dB) indipendentemente dal
valore
La risposta in
continua risulta unitaria, mentre devono essere ottemperate le specifiche sulla
banda passante e sulla banda oscura. In altre parole, si hanno due disequazioni
(le due specifiche) nelle due incognite fB ed N. In questo caso, tuttavia, la
specifica sulla banda passante e' soddisfatta esattamente imponendo fB=f . Si tratta
pertanto di scegliere soltanto l'ordine
Poiche' e' possibile progettare i filtri numerici utilizzando una qualunque unita' di misura dei tempi (e, conseguentemente, delle frequenze), e' conveniente normalizzare tutte le specifiche assumendo T=1. Risulta percio':
-) frequenza di campionamento fc = 1
-) f = 0.1; ovvero w = 0.2 p
-) f = 0.2; ovvero w = 0.4 p
Dato che, per definizione:
|H(f)|dB = 20 log |H(f)| = 10 log |H(f)|
si riscrivono su scala lineare le specifiche, espresse per comodita'
sul quadrato
-) H(0) = 1 (gia' soddisfatta)
-) 1 |H(f)| 0.5 per 0 |f| f (banda passante - gia' soddisfatta)
-) |H(f)| 0.1 per |f| f (banda oscura - da soddisfare)
Applicando quest'ultima diseguaglianza, si ottiene:
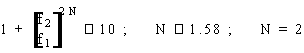
dovendo essere N un intero (specifica su f soddisfatta con margine). I due poli sono pertanto:

ed il filtro analogico risulta quindi essere:
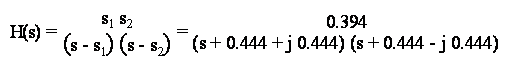
che, decomposta in residui, diviene:
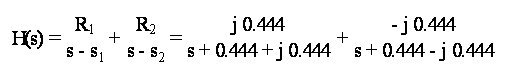
da cui, applicando la (14.1) con T=1, si ottiene:
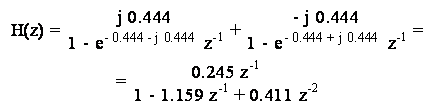
L'equazione alle differenze che implementa il filtro numerico e':
y(n) = 1.159 y(n-1) - 0.411 y(n-2) + 0.245 x(n-1)
Si potrebbe verificare che sussiste uno scostamento fra la risposta in
frequenza analogica H(f) per f=fB=f =0.1 e quella |H(ejw)|
15. Progetto mediante la trasformazione bilineare.
15.1 Teoria.
Anche il metodo della
trasformazione bilineare, come quello dell'invarianza della risposta impulsiva
(argomento
E' allora evidente
come, in base al criterio di Nyquist, non sorga in questo caso il problema
dell'aliasing spettrale della
risposta in frequenza
Per ovviare
all'inconveniente della deformazione delle specifiche, occorre compensare il fenomeno con una pre-deformazione
inversa delle specifiche stesse. Pertanto, in sede di progetto si deforma
l'asse delle frequenze in maniera opposta a quella che la trasformazione
bilineare produrra' inevitabilmente, ottenendo cosi' le specifiche
E' opportuno precisare
che la deformazione delle frequenze sussiste soltanto nelle specifiche di progetto e non
nella risposta
Per ottenere la funzione di trasferimento in z del filtro numerico, la procedura richiede, una volta riportate sulle specifiche analogiche le conseguenze della pre-deformazione spettrale, la trasposizione della funzione di trasferimento del filtro analogico dal dominio continuo a quello a tempo discreto, in base alla semplice regola di conversione dell'operatore continuo di derivazione s, che viene trasposto nel rapporto incrementale, valutato a distanza T:
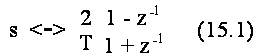
ove T e' il periodo di campionamento. E' interessante notare come
questa trasformazione si applichi direttamente all'espressione in s della
funzione di trasferimento e non richieda quindi, al contrario
15.2 Esercizio (poli complessi coniugati).
Dato il sistema
analogico
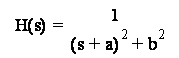
progettare con il metodo della trasformazione bilineare il filtro numerico che ne simula il comportamento.
Svolgimento.
Si tratta dello stessa
funzione di trasferimento dell'esercizio 14.2. Osservando il denominatore di
H(s) si nota immediatamente che, in quanto somma di quadrati, questo deve
presentare radici (poli
- a + j b e - a - j b
Supponiamo sia verificato che a<<1/T e b<<1/T, ove T e' il periodo di campionamento. Allora le caratteristiche in frequenza dopo la trasformazione bilineare rimangono pressocche' immutate. In tale caso, possiamo applicare direttamente la trasformazione (15.1) ottenendo:
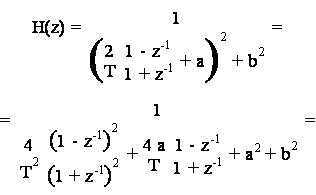
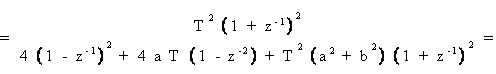
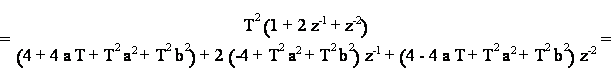

che corrisponde alla seguente equazione alle differenze:
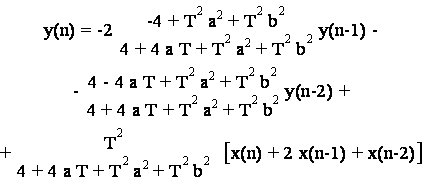
Generalizzando il
procedimento ora illustrato, l'applicazione della trasformazione bilineare
senza pre-distorsione va limitata ai soli casi in cui l'interesse e' confinato
alle basse frequenze (ove la deformazione introdotta e' trascurabile). In
realta', se si desiderasse invece un comportamento in frequenza approssimante
sull'intero spettro quello
15.3 Esercizio (filtro di Butterworth).
Progettare un filtro numerico con il metodo della trasformazione bilineare con le seguenti specifiche:
-) risposta in continua H(0) = 0 dB
-) modulo della risposta in frequenza tale che:
0 dB |H(f)|dB -3 dB per 0 |f| f (banda passante)
monotona decrescente per f |f| f (banda di transizione)
|H(f)|dB -10 dB per |f| f (banda oscura)
-) f = 1 KHz
-) f = 2 KHz
-) frequenza di campionamento fc = 10 KHz
Svolgimento.
Si tratta delle stesse specifiche dell'esercizio 14.3. Le specifiche richieste sono soddisfatte dalla classe dei filtri analogici di Butterworth, definita dalla seguente funzione di trasferimento a soli poli di ordine N:
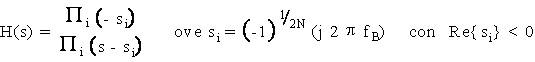
Poiche' e' possibile progettare i filtri numerici utilizzando una qualunque unita' di misura dei tempi (e, conseguentemente, delle frequenze), e' conveniente normalizzare tutte le specifiche assumendo T=1. Risulta percio':
-) frequenza di campionamento fc = 1
-) f = 0.1; ovvero w = 0.2 p
-) f = 0.2; ovvero w = 0.4 p
La trasformazione
bilineare distorce le caratteristiche spettrali contraendo le frequenze
(relative alle specifiche) in base alla relazione non lineare w = 2
arctg (W/2) fra le frequenze normalizzate
(fc=1=T).
Per compensare tale effetto mediante una pre-distorsione opposta dello spettro
e' necessario espandere le specifiche frequenziali con la funzione inversa W = 2
tg (w/2), ovvero F = tg(pf)/p.
In tal modo, le nuove specifiche produrranno, una
Pertanto, le frequenze f ed f sono sostituite, ai fini progettuali, dalle frequenze F ed F :
![]()
![]()
Il modulo quadro della risposta in frequenza dei filtri di Butterworth e', nelle nuove frequenze F:

Percio', la risposta in continua risulta unitaria, mentre devono essere
ottemperate le specifiche sulla banda passante e sulla banda oscura. In altre
parole, si hanno due disequazioni (le due specifiche) nelle due incognite FB ed N. In
questo caso, tuttavia, la specifica sulla banda passante e' soddisfatta
esattamente imponendo FB=F . Si tratta pertanto di scegliere soltanto l'ordine
Dato che, per definizione:
|H(F)|dB = 20 log |H(F)| = 10 log |H(F)|
si riscrivono le specifiche, espresse per comodita' sul quadrato
-) H(0) = 1 (gia' soddisfatta)
-) 1 |H(F)| 0.5 per 0 |F| F (banda passante - gia' soddisfatta)
-) |H(F)| 0.1 per |F| F (banda oscura - da soddisfare)
Applicando quest'ultima diseguaglianza, si ottiene:
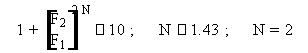
dovendo essere N un intero (specifica su F soddisfatta con margine).
I due poli sono pertanto:
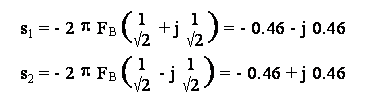
ed il filtro analogico risulta quindi essere:
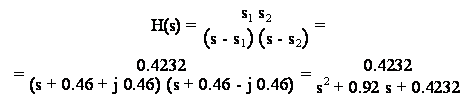
che, con la sostituzione (17.1) per T=1, diviene:
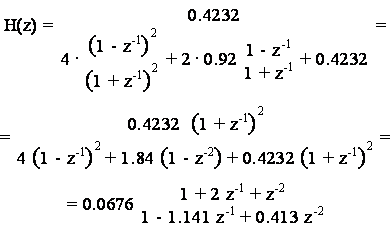
Pertanto, l'equazione alle differenze che implementa il filtro numerico e':
y(n) = 1.141 y(n-1) - 0.413 y(n-2) +
+ 0.0676 x(n) + 2 x(n-1) + x(n-2)
Si noti come questa implementazione sia diversa da quella ottenuta con la tecnica dell'invarianza impulsiva, sopratutto a causa della presenza di una parte FIR nel filtro numerico.
E' proprio questa parte FIR che garantisce l'assenza di aliasing spettrale a causa dello zero doppio in z=-1, ovvero w=p.
16. Progetto mediante il campionamento in frequenza.
16.1 Teoria.
Il metodo
In pratica, se la sequenza della risposta impulsiva e' lunga N, si progetta un filtro composto dal parallelo di N filtri risonanti complessi di tipo IIR, accordati a ciascuna delle N frequenze considerate (tra 0 e 2p). L'ingresso a tale schema e' costituito da un filtro FIR i cui zeri giacciono sul cerchio unitario, proprio in corrispondenza ai poli prodotti dai filtri risonanti. La perfetta cancellazione poli-zeri consente di ottenere per il sistema globale una funzione di trasferimento in z a soli zeri di lunghezza limitata, cosicche' il filtro progettato con la tecnica del campionamento in frequenza, benche' presenti al suo interno elementi IIR, risulta sempre di tipo FIR.
L'espressione della
funzione di trasferimento in z di un filtro progettato con la tecnica
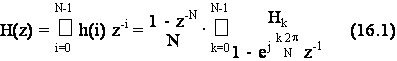
ove Hk
sono i campioni in frequenza
(equispaziati tra 0 e 2p) di H(w) ovvero, equivalentemente, i campioni di
H(z) in punti equispaziati

Il sistema espresso dalla (16.1) e' in generale complesso. Tuttavia esso presenta una implementazione reale se, come e' ovvio, la sequenza della risposta impulsiva e' reale, ovvero, equivalentemente, se la sua trasformata di Fourier (e quindi anche i suoi campioni) gode della proprieta' di simmetria coniugata.
Per ovviare ai problemi di stabilita' ed ai consistenti errori di quantizzazione dovuti ai blocchi IIR, anziche' campionare la trasformata-z sul cerchio unitario (equivalente alla trasformata di Fourier) il progetto puo' venire effettuato campionando la trasformata-z su punti equispaziati leggermente interni al cerchio unitario. Ovviamente, anche la parte FIR, dovendo cancellare i poli, dovra' possedere gli stessi zeri interni al cerchio unitario.
Il metodo
Dal punto di vista
16.2 Esercizio.
Disegnare la
struttura, basata sul campionamento in
frequenza,
H(z) = (1 - z )
Svolgimento.
Sviluppando formalmente il cubo si ottiene:
H(z) = 1 - 3 z + 3 z - z
che corrisponde alla sequenza della risposta impulsiva:
h(n) = d(n) - 3 d(n-1) + 3 d(n-2) - d(n-3)
Poiche' la durata di
h(n) e' N=4 campioni, per progettare il filtro con la tecnica
Scegliendo, per semplicita', quest'ultima strada, si ottiene:
H = H(ej0) = H(1) = 1 - 3 + 3 - 1 = 0
H = H(ejp ) = H(j) = 1 + 3 j - 3 - j = -2 + 2 j
H = H(ejp) = H(-1) = 1 + 3 + 3 + 1 = 8
H = H(ej3p ) = H(-j) = 1 - 3 j - 3 + j = -2 - 2 j
Si potrebbe facilmente verificare, calcolando la DFT, che:
DFT =
Si noti come H ed HN/2 siano reali, mentre i restanti Hk ed HN-k risultino complessi coniugati fra loro. Cio' accade sempre quando la risposta impulsiva e' reale e consente, come si vedra' nel seguito, uno schema a coefficienti reali invece che complessi.
Analiticamente si ottiene la seguente funzione di trasferimento in z:
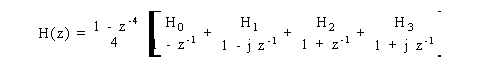
che e' implementabile in modo poco efficiente con un'aritmentica complessa come in fig. 16.1.
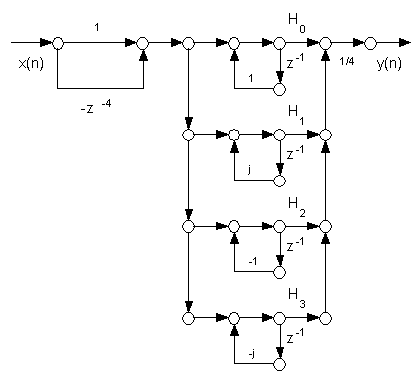
Fig. 16.1. Implementazione complessa del filtro numerico H(z).
Lo schema e' pero' semplificabile. Innanzitutto, il blocco con H =0 puo' essere omesso con un risparmio di operazioni. Inoltre, i blocchi complessi del primo ordine possono essere facilmente accoppiati per dar luogo a blocchi del secondo ordine a coefficienti reali. In particolare, sviluppando analiticamente l'espressione complessa di H(z) teste' trovata, si ottiene:
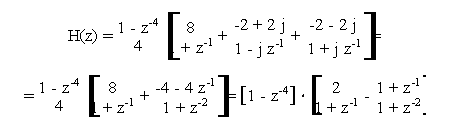
che e' efficientemente implementabile come illustrato in fig. 16.2.
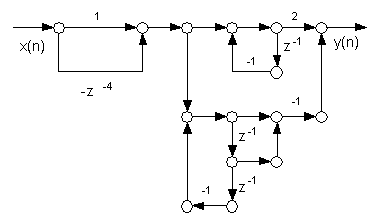
Fig. 16.2. Implementazione efficiente del filtro numerico H(z).
Parte IV. Analisi statistica e stime spettrali.
17. Errori di quantizzazione.
17.1 Teoria.
Ogni segnale a tempo discreto, rappresentato con un numero finito di bit, porta con se' un errore dovuto al troncamento o, piu' frequentemente, all'arrotondamento dei valori analogici assunti. Alla sequenza di errore cosi' ottenuta si da' il nome di rumore di quantizzazione.
In realta', il rumore di quantizzazione dipende dai valori istantaneamente assunti dal segnale. Ma, poiche' e' assai difficile valutare deterministicamente l'entita' di tale errore, dipendente dai valori assunti dal segnale, se ne effettua un'analisi statistica modellando la sequenza di segnale e l'errore di quantizzazione come realizzazioni di processi aleatori.
Solitamente, per semplificare l'analisi, si assume che il rumore di quantizzazione sia realizzazione di un processo stazionario, a distribuzione uniforme, bianco ed incorrelato con il segnale.
La valutazione dell'entita' del rumore di quantizzazione in rapporto alla potenza del segnale, unita ai requisiti di dinamica e risoluzione, e' determinante nella progettazione di sistemi numerici. Per meglio comprendere cio', nell'esercizio seguente sara' analizzato il caso di aritmetica in virgola fissa, spesso adoperata negli elaboratori numerici di segnale veloci.
Nei dispositivi in virgola fissa, la sorgente di errore di quantizzazione e' l'operazione di moltiplicazione. Invece, l'operazione di addizione e' effettuata senza alcun errore, sempre che la dinamica del sistema sia stata adeguatamente progettata per garantire l'assenza di traboccamento (overflow), ovvero che il risultato rientri nell'intervallo dei numeri rappresentabili con i bit disponibili (requisito di dinamica).
Al fine di analizzare il comportamento del filtro in esame nei riguardi del rumore, e' utile determinare le funzioni di trasferimento rumore-uscita di ogni singola sorgente di rumore, posta subito dopo ogni moltiplicazione, per combinarne i risultati mediante la sovrapposizione degli effetti.
Al riguardo, e' opportuno notare che un sistema di tipo FIR definito dall'equazione alle differenze:
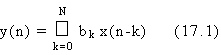
presenta un legame diretto ingresso-uscita, per cui i rumori si sommano semplicemente. Pertanto detto si la varianza di ogni generatore di rumore, la varianza di rumore in uscita su risulta:
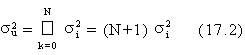
Al contrario, l'effetto in uscita di generatori di rumore in blocchi IIR va pesato con le rispettive funzioni di trasferimento rumore-uscita. In particolare, se lo schema di flusso prevede che tutti i generatori di rumore agiscano direttamente sull'ingresso, come nel caso:
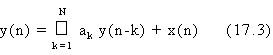
la funzione di trasferimento rumore-segnale coincide per tutti i generatori con quella del filtro in esame (cioe' Z). Per cui, la varianza di rumore in uscita su corrisponde a quella in ingresso si in base alla relazione:
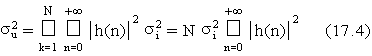
E' questo il caso, ad esempio, di un sistema IIR del primo ordine del tipo:
y(n) = a y(n-1) + x(n) (17.5)
per il quale la varianza di uscita si risulta in funzione di quella di ingresso si in base alla semplice espessione:
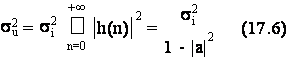
17.2 Esercizio.
Dato il filtro numerico FIR definito dalla seguente funzione di trasferimento in Z:
H(z) = 0.8 + 0.4 z
si valuti il rapporto segnale/rumore di quantizzazione (si supponga il filtro realizzato con aritmetica in virgola fissa con 7 bit piu' segno) in uscita al filtro quando in ingresso e' presente una sequenza di rumore che e' realizzazione di un processo stazionario gaussiano bianco di varianza unitaria.
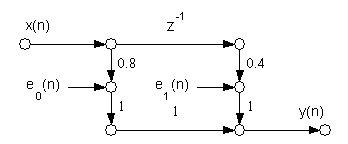
Fig. 17.1. Grafo di H(z) con i generatori di rumore di quantizzazione.
Svolgimento.
Dato che i segnali sono quantizzati, nello schema di fig. 17.1 sono presenti le sorgenti di rumore e (n) ed e (n), una per ogni prodotto, che supponiamo incorrelati con il segnale e tra loro stessi.
Per poterne valutare il contributo sull'uscita in termini di potenza di rumore, e' necessario progettare i quantizzatori con dinamica e risoluzione opportune.
La dinamica deve consentire la rappresentazione, senza saturazione, di qualunque valore assunto dai segnali che attraversano il sistema in ogni punto del sistema stesso. Nel sistema di fig. 17.1 e' sufficiente imporre tale condizione all'ingresso ed all'uscita. Allora, detti xMAX il massimo ingresso ed yMAX la massima uscita, deve essere scelto un valore massimo rappresentabile sMAX tale che:
![]()
che garantisce l'assenza di traboccamento (overflow).
Una volta scelta la dinamica, la risoluzione D, cioe' la differenza fra livelli discreti contigui per quantizzazioni uniformi, dipende dal numero di bit (b+1). Essa e' infatti:
D = 2-b sMAX
Sono percio' rappresentabili tutti i valori compresi in [-sMAX , sMAX] con risoluzione D.
L'errore di quantizzazione nel caso di arrotondamento e' limitato entro l'intervallo [-D/2 , D/2]. La varianza di tale errore, assunto con distribuzione uniforme, e' pari a:
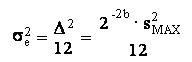
In questo esercizio, vi sono due sorgenti di rumore (e (n) ed e (n)) che confluiscono direttamente in uscita (eq. (17.1)). Pertanto la varianza del rumore di uscita (eq.(17.2)) e':
![]()
Per calcolare la potenza del segnale in uscita (per ingresso bianco) basta ricordare che:
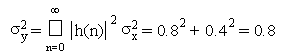
Per valutare il rapporto segnale/rumore (SNR) in uscita al filtro bisogna fissare il valore sMAX. Essendo a distribuzione gaussiana, il suo massimo risulterebbe infinito. Tuttavia, e' possibile scegliere per xMAX un valore finito tale che esso superi sMAX raramente, ovvero che l'area della densita' di probabilita' oltre quel valore sia trascurabile. Ad esempio, se si osserva che |x(n)|>4sx con probabilita' <10 , e' possibile scegliere xMAX=4sx=4. Il criterio adottato garantisce la presenza di overflow su meno di un campione su diecimila. In tal caso, il campione e' tosato (quantizzazione con saturazione) per limitarne l'errore di rappresentazione.
Dopo aver imposto la dinamica di ingresso dobbiamo controllare quella di uscita. Sovente, non conoscendo l'evoluzione a priori dell'uscita del sistema, ci si cautela con le scelte:
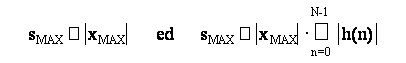
ove h(n) e' la risposta impulsiva del filtro, ottenendo in tal caso sMAX=4.8. Si osservi che quello adottato e' un criterio conservativo, poiche' il fatto che l'ingresso sia entro la dinamica massima implica, in questo caso, che anche l'uscita rimanga entro la dinamica.
Il rapporto SNR risulta quindi:

Si noti come un criterio meno drastico su xMAX ed sMAX (ad esempio xMAX=2sx=2 ed sMAX=1.2xMAX=2.4) avrebbe comportato una migliore risoluzione (un fattore 2) ed un migliore SNR (un fattore 4 corrispondente a 6 dB), ma la probabilita' di saturazione sarebbe cresciuta da qualcosa meno di 10 a qualcosa meno di 5 10 , con effetti distorcenti nel 5 % dei campioni di .
18. Calcolo di momenti in sistemi non-lineari.
18.1 Teoria.
Ci siamo sinora occupati di studiare il comportamento di sistemi lineari a tempo discreto, anche mediante la valutazione di momenti dei processi di ingresso e/o di uscita. Tuttavia, in alcune applicazioni la relazione che lega l'ingresso e l'uscita non e' di tipo lineare.
Per studiare tali sistemi, si ricorre talvolta ad una linearizzazione locale. Questo procedimento, pero', presenta lo svantaggio di non permettere un'analisi globale del comportamento del sistema, anche perche' i coefficienti divengono spesso, in quanto funzioni del punto di lavoro, non piu' costanti ma funzioni del tempo. Risulta pertanto preferibile, laddove possibile, un'analisi del sistema non-lineare che consideri integralmente la relazione intercorrente fra l'ingresso e l'uscita.
Fra i sistemi non-lineari, quelli piu' facilmente analizzabili sono quelli istantanei, ovvero del tipo:
y(n) = f[x(n)] (18.1)
ove la sequenza di ingresso x(n) e quella di uscita y(n), come pure il loro legame campione per campione dato dalla funzione (18.1), possono essere reali od anche complesse.
Dato che per funzioni non singolari vale lo sviluppo in serie di potenze, e' possibile esprimere una non-linearita' istantanea reale come segue:
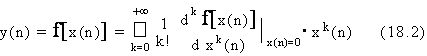
ove si e' supposto, per comodita', di sviluppare la (18.1) nell'origine.
Per funzioni complesse e/o di variabili complesse, la (18.2) diviene solo formalmente piu' complicata. In realta', esiste la possibilita' di sviluppare analogamente la (18.1), in funzione della variabile complessa o, se cio' e' piu' conveniente, delle rispettive parti reali e immaginarie, od anche del modulo e fase.
Dato che i coefficienti tendono in pratica a decrescere asintoticamente (e, spesso, rapidamente) con il proprio esponente, sono gli ordini piu' bassi (i termini quadratici e cubici) a rivestire particolare importanza nello studio dei sistemi non-lineari istantanei. Percio', nell'esempio che segue e' stato considerato il caso emblematico di un quadratore di un segnale reale.
18.2 Esercizio (quadratore).
Dato un sistema non-lineare con ingresso la sequenza reale w(n) ed uscita la sequenza reale y(n), avente una caratteristica del tipo:
y(n) = [x(n)]
ove
x(n) = w(n) - w(n-1)
determinare la sequenza di autocorrelazione Ryy(k) del processo di uscita , quando in ingresso e' presente un processo stazionario gaussiano bianco di varianza s .
Svolgimento.
Il processo e' costituito dall'uscita di un quadratore nel quale entra il processo avente una sequenza di autocorrelazione Rxx(k), che calcoleremo dopo. L'autocorrelazione Ryy(k) risulta:
Ryy(k) = E[y(i)y(i+k)] = E =
= E E + 2 =
= Rxx(0) + 2 Rxx(k)
ove si e' sfruttata la proprieta' del momento del quarto ordine (denominato in letteratura four-fold moment) di variabili gaussiane, che consente di calcolare, date le quattro variabili congiuntamente gaussiane a, b, c, d, la seguente espressione:
E[a b c d] = E[a b] E[c d] + E[a c] E[b d] + E[a d] E[b c]
Percio', essendo:
Rxx(k) = s [ 2 d(k) - d(k-1) - d(k+1) ]
ove:
![]()
si ottiene:
Ryy(k) = s [ 4 + 8 d(k) + 2 d(k-1) + 2 d(k+1) ]
Si noti come l'autocorrelazione Ryy(k) e' sempre positiva. Infatti, l'uscita di un quadratore e' un segnale a valor medio non nullo, trattandosi di valori attesi di variabili sempre non negative.
19. Progetto di filtri ai minimi quadrati.
19.1 Teoria.
I metodi di progetto illustrati nella parte III si basano su criteri determinati indipendentemente dalle caratteristiche statistiche dei processi in ingresso ed uscita al filtro da progettare. Proprio per questa peculiarita' sono da preferirsi quando dette statistiche non sono note ne' possono essere facilmente o correttamente stimate.
Al contrario, se si conoscono le statitistiche del processo di ingresso sino al secondo ordine, e' possibile seguire una strada progettuale diversa, basata su un criterio di ottimalita'. In particolare, la tecnica dei minimi quadrati (denominato anche filtraggio di Wiener) minimizza l'errore quadratico medio del segnale y(n) ottenibile in uscita, rispetto a quello desiderato d(n), ovvero la funzione di costo: E |y(i)-d(i)| .
Tale metodo consente il progetto di filtri FIR di ordine N qualunque ma prefissato, cioe' con N+1 coefficienti, posizionati a partire dall'istante generico n=M. In altre parole, la trasformata Z del filtro da progettare e':
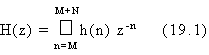
Per applicare tale metodo e' necessario conoscere la sequenza di autocorrelazione Rxx(k)=E[x (i)x(i+k)] del processo stazionario in ingresso al filtro h(m) per -N k N e la sequenza di crosscorrelazione Rxd(n)=E[x (i)d(i+n)] fra l'ingresso e l'uscita desiderata per M n≤M+N. I coefficienti del filtro h(n) sono dati dalla soluzione del seguente sistema espresso in forma matriciale:
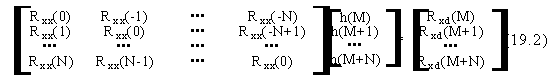
che ha per soluzione:

Per calcolare la matrice inversa della sequenza di autocorrelazione richiesta nella eq. (19.3) si puo' utilizzare, al posto delle tecniche convenzionali per matrici generiche (metodo dei minori o algoritmi numerici eventualmente implementabili su macchine calcolatrici) una procedura semplificata che ne consente il calcolo simbolico e che sara' illustrata in un prossimo capitolo.
Riguardo al metodo dei minimi quadrati, si osservi che la matrice [Rxx(k)] e' diagonale se il processo e' bianco. In tal caso, la soluzione ottima consiste banalmente nel finestrare per M n≤M+N la Rxd(n). Percio', fissata la risposta in frequenza del filtro desiderato D(w), il progetto di filtri FIR con il metodo della finestra rettangolare, analizzato in un capitolo precedente, risulta ottimo con il criterio dei minimi quadrati se il processo di ingresso e' bianco.
Al fine di controllare la correttezza delle espressioni matriciali, si puo' inoltre osservare come, sempre per ingresso bianco, la crosscorrelazione ingresso-uscita Rxd(n) deve risultare causale per h(n) causale. Infatti l'uscita attuale di un filtro causale con ingresso bianco non puo' mai dipendere dal futuro degli ingressi.
19.2 Esercizio.
Un sistema di trasmissione e' studiato riferendosi a sistemi e segnali a tempo-discreto, supponendo possibile un campionamento perfetto (con periodo T=1) delle corrispondenti grandezze analogiche. In tale sistema di comunicazione, viene inviato al canale, caratterizzato da una risposta h(n), un segnale di informazione d(n). Il segnale ricevuto r(n)=u(n)+w(n) e' la somma del segnale utile u(n)=d(n) h(n) e di un rumore bianco indipendente w(n).
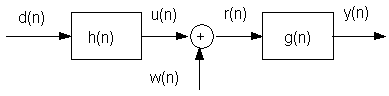
Fig. 19.1. Schema a blocchi del sistema tempo-discreto di comunicazione.
Tali modelli sono descritti come segue:
h(n) = d(n) - 0.25 d(n-2)
sw = Rww(0) = E[|w(i)| ] = 0.021
Rdd(k) = E[d (i)d(i+k)] = -0.25 d(n+2) + 0.5 d(n) - 0.25 d(n-2)
Progettare un filtro FIR con risposta impulsiva g(n) a 3 coefficienti per la equalizzazione di canale, ovvero per la ricostruzione ottima di d(n) a partire da r(n), e valutare il rapporto segnale/rumore (SNR) ottenibile in uscita al filtro g(n).
Svolgimento.
Sia y(n)=r(n) g(n) l'uscita del filtro da progettare g(n). Applicando il metodo dei minimi quadrati con l'obbiettivo y(n)=d(n), il problema e' risolto dalla (19.3), cioe' la soluzione del sistema (19.2). Occorre pertanto calcolare le grandezze statistiche che compaiono in tale sistema. Valutiamo in primo luogo la sequenza di autocorrelazione Rrr(k) del processo .
Rrr(k) = E[r (i)r(i+k)] = E =
= E[u (i)u(i+k)] + E[w (i)w(i+k)] = Ruu(k) + sw d(k)
essendo i processi di segnale utile e rumore fra loro indipendenti. La sequenza di autocorrelazione Ruu(k) di e':
Ruu(k) = E[u (i)u(i+k)] = Rdd(k) Chh(k) = Rdd(k) [h(-k) h(k)] =
= Rdd(k) [1.06 d(k) - 0.25 d(k+2) - 0.25 d(k-2)] =
= 0.06 d(k+4) - 0.39 d(k+2) + 0.66 d(k) - 0.39 d(k-2) + 0.06 d(k-4)
Calcoliamo adesso la sequenza di crosscorrelazione Rry(k) fra il processo di ingresso al filtro g(n) e quello dell'uscita desiderata =, ricordando che e sono stazionari e fra loro indipendenti:
Rry(k)=Rrd(k)= E[r (i)d(i+k)] = E = E[u (i)d(i+k)] =
= E[d(i)u (i-k)] = Rdu (-k) = [Rdd(k) h(-k)] = Rdd(k) h(-k) =
= 0.06 d(k+4) - 0.375 d(k+2) + 0.56 d(k) - 0.25 d(k-2)
La soluzione del problema richiede che vadano scelti 3 campioni consecutivi della funzione Rry(k) che si estende in realta' fra k=-4 sino a k=2 (cioe' per 7 campioni consecutivi). Per fare cio' sarebbe necessario valutare con un criterio di bonta' (ad esempio: massimo SNR in uscita) le diverse scelte dopo aver progettato tutti e 5 i filtri possibili.
Tuttavia, una scelta sub-ottima, solitamente adottata in questo caso, consiste nello scegliere quei campioni della crosscorrelazione Rry(k) con la energia massima, cioe' per cui la quantita' reale e positiva
Ery(3)=|Rry(M)| +|Rry(M+1)| +|Rry(M+2)|
risulta massima al variare di M. Tale criterio impone, in questo caso, M=-2. Il sistema diviene pertanto:
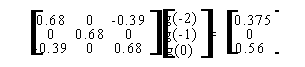
che, risolto il sistema lineare, fornisce la soluzione:
[ g(-2) , g(-1) , g(0) ]T = [ -0.12 , 0 , 0.77 ]T
Essendo poi:
Cgg(-k) = [g(-k) g(k)] = -0.09 d(k+2) + 0.6 d(k) - 0.09 d(k-2)
la potenza di segnale utile in uscita risulta:
syu = Ruu(k) Cgg(k) |k=0 = 0.47
mentre quella di rumore in uscita e':
syw = sw Cgg(0) = 0.013
che corrisponde ad un SNR, espresso in dB (cioe' pari alla quantita' 10 log syu /syw ), pari a 15.7 dB.
La scelta non ottimale M=0 avrebbe tuttavia comportato un filtro g(n) causale. Il sistema lineare da risolvere diviene:
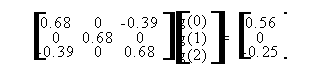
mentre i risultati numerici di questa scelta alternativa sono qui di seguito riportati:
[ g'(0) , g'(1) , g'(2) ]T = [ 0.94 , 0 , 0.165 ]T
s'yu = = 0.475
s'yw = 0.019
SNR' = 14 dB
Come si prevedeva, il rapporto SNR in uscita al filtro g'(n) risulta peggiore rispetto al caso ottimale (con il filtro g(n)).
20. Stima spettrale autoregressiva.
20.1 Teoria.
L'informazione su un processo osservato tramite una o piu' realizzazioni di durata limitata non consente in generale una misura esatta di grandezze statistiche del processo in esame, quali la sequenza di autocorrelazione oppure, equivalentemente, lo spettro di densita' di potenza, che ne costituisce la trasformata di Fourier.
E' noto dalla teoria della stima spettrale che il metodo del periodogramma, eventualmente mediato su piu' intervalli di osservazione per assicurarne la consistenza, si basa su una misura oggettiva della parte osservata del processo, senza alcuna ipotesi sulla parte non osservata. In particolare, la risoluzione spettrale e' limitata dalla durata degli intervalli di osservazione.
Al contrario, esistono metodi soggettivi che impongono ipotesi o vincoli sulla parte non osservata delle realizzazioni. In tal modo, la risoluzione spettrale puo' accrescersi in maniera considerevole, condizionatamente al fatto che le ipotesi assunte siano effettivamente vere.
Il vincolo che si impone nella stima spettrale autoregressiva (AR) e' che il processo osservato e' statisticamente equivalente a quello ottenibile come uscita di un sistema fittizio di tipo IIR con in ingresso un processo bianco caratterizzato da una data varianza. Il sistema e' detto il modello AR equivalente, mentre il processo bianco e' detto processo di eccitazione (o, talvolta, di innovazione).
Il metodo di stima spettrale AR e' ovviamente indicato per processi che sono davvero AR per loro natura. Altrimenti, sussiste un inevitabile errore dovuto al modello non corrispondente alla realta'.
Vi e' inoltre da osservare che la stima del modello non e' effettuata in pratica a partire dalla sequenza di autocorrelazione vera, ma da una sua stima solitamente a partire da un'osservazione di durata limitata. Cio' provoca errori nei campioni della sequenza di autocorrelazione Rxx(k) che inducono quindi errori sul modello e sullo spettro AR stimati.
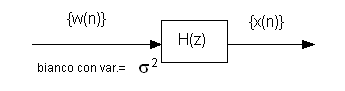
Fig. 20.1. Modello del processo .
Si tratta percio' di stimare un modello AR come in fig. 20.1, caratterizzato dalla funzione di trasferimento H(z), di tipo IIR con N poli:
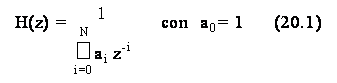
ovvero dalla corrispondente equazione alle differenze:
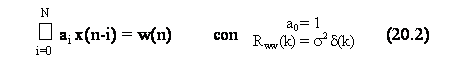
ove le incognite sono la varianza s del processo di eccitazione ed i restanti N coefficienti ai del filtro H(z) di ordine N, il cui primo coefficiente e' sempre unitario.
In conseguenza, lo spettro di densita' di potenza del processo di uscita (spettro AR) risulta essere dato da:
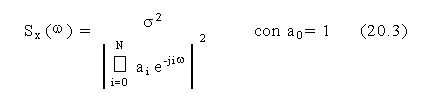
Le incognite sono determinate come soluzioni del seguente sistema lineare (equazioni di Yule-Walker), data la sequenza di autocorrelazione Rxx(k)=E[x (i)x(i+k)], nel caso N 1:
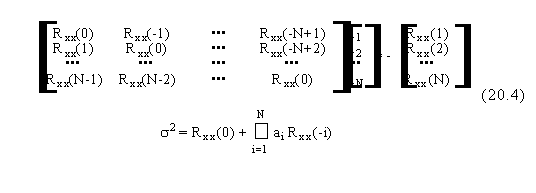
Ovviamente, nel caso N=0, risulta banalmente s =Rxx(0).
E' utile osservare che il metodo di modellizzazione e stima spettrale si applica a processi sia reali che complessi. In quest'ultimo caso, i coefficienti del filtro H(z) risulteranno in generale complessi.
20.2 L'algoritmo ricorsivo di Levinson-Durbin.
Per risolvere il sistema (20.4) e' di grande aiuto teorico e pratico l'algoritmo di Levinson-Durbin. Oltre al costo computazionale ridotto, tale metodo e' importante perche' costituisce una soluzione iterativa nei riguardi dell'ordine N del modello. L'algoritmo calcola ricorsivamente gli insiemi di incognite , , , ..., . L'insieme finale e' la soluzione desiderata per l'ordine N. In particolare, l'algoritmo e' inizializzato per l'ordine 0 con:
s = Rxx(0) (20.5)
quindi, per l'ordine 1 si ottiene:
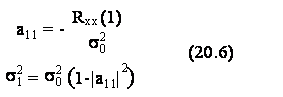
mentre la generica recursione per n=2,..,N risulta:

E' importante rilevare che la soluzione finale coincide con la soluzione del sistema (20.4).
L'ordine N del modello AR e' un parametro molto importante nella modellistica spettrale, perche' determina la capacita' di risoluzione spettrale del modello scelto. In generale, un ordine piu' elevato consente una risoluzione spettrale maggiore. Ma cio' puo' provocare la presenza di picchi spuri o lo sdoppiamento (splitting) di picchi singoli nello spettro stimato.
Normalmente l'ordine N non e' noto e deve essere determinato con un qualche criterio. Se non si hanno conoscenze a priori, si puo' aumentre progressivamente il valore di N sino a che la varianza s del processo di eccitazione (decrescente con N) non risulta diminuire in maniera giudicata trascurabile. Infatti, per valori di N maggiori dell'ordine vero, sussiste sempre una diminuzione della varianza stimata del processo di eccitazione dovuta agli errori nei valori di correlazione stimati dai dati. In ogni caso, tale varianza e' limitata inferiormente dalla varianza del vero processo informativo di ingresso.
Risulta pertanto evidente il vantaggio dell'algoritmo iterativo di Levinson-Durbin consistente nel fatto che esso permette di calcolare il modello AR per un ordine N in funzione dei parametri relativi al modello AR di ordine N-1.
20.3 Esercizio.
Dato un processo con autocorrelazione Rxx(k) data da:
Rxx(k) = 0.125 [d(k+2)+d(k-2)] + 0.562 [d(k+1)+d(k-1)] + 0.884 d(k)
calcolare lo spettro AR di secondo ordine usando la recursione di Levinson-Durbin.
Svolgimento.
Partiamo dall'ordine 0; dall'eq. (20.5) si ottiene:
s = Rxx(0) = 0.844
Quindi, applicando le (20.6), per l'ordine 1 si ha:
a = - Rxx(1) / s = - 0.636
s = s (1 - |a | ) = 0.527
Infine, data la (20.7) con N=2:
a = - [Rxx(2) + a Rxx(1)] / s = 0.441
a = a + a a = - 0.906
s = s (1 - |a | ) = 0.424
Il modello AR del secondo ordine dato dalla (20.1), avente in ingresso un processo bianco (processo di eccitazione) di varianza s , e' pertanto:
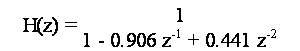
mentre, essendo s = 0.424, la stima spettrale AR, in base alla eq. (20.3), risulta:
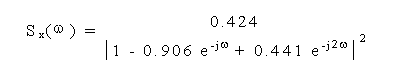
21. Predizione lineare ottima.
21.1 Teoria.
Dato un certo fenomeno osservabile (ad esempio: valore assunto da una grandezza fisica, voto assegnato agli esami universitari, tasso di cambio della lira rispetto al dollaro), di cui e' noto il passato sino al tempo presente, quale sara' il suo andamento futuro? La domanda ora posta rappresenta un classico problema della teoria della stima: la predizione.
Osservando una
sequenza realizzazione di un processo stazionario , ci si puo' porre il
problema di predire il campione futuro
x(n+1), mediante il predittore ![]() (n+1),
a partire dalla conoscenza del campione attuale x(n) e degli N ultimi
campioni passati [x(n-1), x(n-2), ..., x(n-N)]. In realta', nel caso ora
illustrato si parla di predizione lineare ad
un passo, sottintendendo che la predizione lineare a due o M passi consista
nel predire x(n+2) o x(n+M), mediante i loro rispettivi predittori
(n+1),
a partire dalla conoscenza del campione attuale x(n) e degli N ultimi
campioni passati [x(n-1), x(n-2), ..., x(n-N)]. In realta', nel caso ora
illustrato si parla di predizione lineare ad
un passo, sottintendendo che la predizione lineare a due o M passi consista
nel predire x(n+2) o x(n+M), mediante i loro rispettivi predittori ![]() (n+2)
e
(n+2)
e ![]() (n+M). Nel seguito faremo riferimento al caso di
predittori
(n+M). Nel seguito faremo riferimento al caso di
predittori ![]() (n+1)
ad un passo, ma la teoria esposta e' di facile generalizzazione per passi
multipli.
(n+1)
ad un passo, ma la teoria esposta e' di facile generalizzazione per passi
multipli.
La predizione e' lineare se e' effettuata combinando linearmente gli N ultimi campioni conosciuti, cioe':
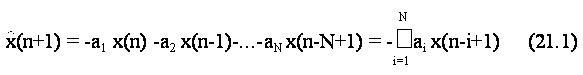
per cui il predittore lineare p(n) ha la seguente risposta impulsiva:
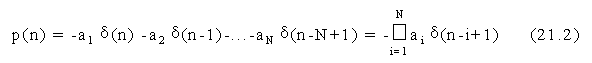
corrispondente alla funzione P(z) di trasferimento in z, di ordine N-1:
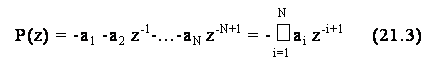
Il predittore definito dalle (21.2)-(21.3) e' detto predittore di ordine N-1 (cioe': un filtro FIR ad N coefficienti). In particolare, sovente rivestono interesse applicativo per la loro semplicita' computazionale il predittore di ordine zero (ZOP-Zero Order Predictor), cioe' ad un solo coefficiente, ed il predittore di ordine uno (FOP-First Order Predictor) a due coefficienti.
Per valutare la bonta' della predizione effettuata, si puo' analizzare statisticamente l'errore di predizione , definito come:
e(n) = x(n) - ![]() (n) (21.4)
(n) (21.4)
L'errore di predizione, in virtu' della (21.1), puo' essere esplicitato in funzione dei campioni del processo , cioe':
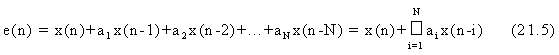
ovvero nel dominio z:
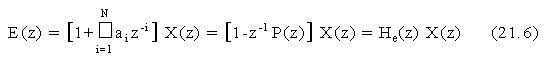
ove e' stato definito He(z)=1-z P(z).
Il sistema He(z) di ordine N
e' un filtro FIR avente N+1
coefficienti; esso e' detto filtro
dell'errore di predizione lineare in quanto consente di ottenere in uscita
l'errore di predizione lineare e(n), data in ingresso la sequenza dei campioni
osservati x(n). Si noti che il ritardo su P(z) e' necessario poiche' bisogna
attendere l'osservazione del campione vero x(n+1) per confrontarlo con quello
stimato ![]() (n+1).
(n+1).
Per progettare un predittore lineare, che e' un filtro FIR, con il metodo dei minimi quadrati ci si puo' avvalere della soluzione del sistema (19.2), ove si e' posto come segnale desiderato proprio d(n)=x(n+1). Pertanto si ottiene:
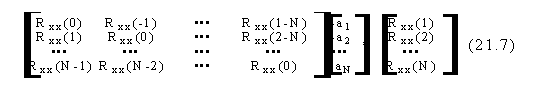
E' fondamentale osservare che il sistema (21.7) e' identico a quello che definisce i coefficienti AR nelle equazioni di Yule-Walker date dalla (20.4). Percio', anche la soluzione del problema sara' identica ed gli N coefficienti possono esssere indifferentemente interpretati come i coefficienti del modello AR di ordine N ovvero i coefficienti del predittore lineare ottimo ad un passo di ordine N-1.
Inoltre, stante l'identita' dei coefficienti , risulta che: He(z)=H (z), ove H(z) e' il modello AR di ordine N dato dalla (20.1). In altre parole, il filtro dell'errore di predizione lineare He(z), che e' un filtro FIR di ordine N, coincide con il filtro inverso del modello AR.
Pertanto, le caratteristiche statistiche del processo dell'errore di predizione possono essere valutate come uscita del filtro He(z) operante sul processo . In particolare, la varianza dell'errore di predizione, ottenuta con un predittore lineare ottimo ad un passo di ordine N-1, corrisponde alla varianza dell'uscita del filtro He(z) di ordine N e quindi coincide con la varianza stimata del processo di eccitazione del modello AR di ordine N.
Si noti, inoltre, che se la modellizzazione AR di ordine N del processo fosse corretta, l'errore di predizione sarebbe, per definizione, un processo bianco. Allora, il filtro He(z) di ordine N risulterebbe essere anche un filtro sbiancante del processo .
Si osservi, infine,
che i coefficienti del filtro predittore, come del resto quelli del modello AR, dipendono dai valori assunti
dall'autocorrelazione del processo . In particolare, se il processo
e' bianco, i coefficienti sono tutti nulli, dato il processo
non necessita di essere sbiancato. Al contrario, se un certo coefficiente di
correlazione (supponiamo quello a distanza k) tende all'unita', la predizione
ottima non puo' che consistere nel valore assunto dal segnale k passi prima,
cioe': ![]() (n)=x(n-k).
(n)=x(n-k).
21.2 Esercizio.
Dato un processo con autocorrelazione Rxx(k) data da:
Rxx(k) = 0.125 [d(k+2)+d(k-2)] + 0.562 [d(k+1)+d(k-1)] + 0.884 d(k)
determinare i predittori lineari ottimi di ordine zero (ZOP) e uno (FOP), cioe' ad uno e due coefficienti, rispettivamente. Si calcolino inoltre le funzioni di trasferimento in z dei filtri degli errori di predizione, nonche' le varianze di questi ultimi.
Svolgimento.
Si tratta dello stesso processo dell'esecizio 20.3. Utilizzandone i risultati ottenuti con l'algoritmo di Levinson-Durbin per N=1:
a = - 0.636
s = 0.527
il predittore ZOP e':
![]() (n+1)
= 0.636 x(n)
(n+1)
= 0.636 x(n)
ovvero
P (z) = 0.636
mentre il filtro dell'errore di predizione e':
He0(z) = 1 - z P (z) = 1 - 0.636 z
e 0.527 e' la corrispondente varianza dell'errore di predizione.
Inoltre, essendo per N=2:
a = 0.441
a = - 0.906
s = 0.424
quindi il predittore FOP risulta:
![]() (n+1)
= 0.906 x(n) - 0.441 x(n-1)
(n+1)
= 0.906 x(n) - 0.441 x(n-1)
cioe'
P (z) = 0.906 - 0.441 z
mentre il filtro dell'errore di predizione diviene:
He1(z) = 1 - z P (z) = 1 - 0.906 z + 0.441 z
e 0.424 e' la varianza dell'errore di predizione, ottenuta con quest'ultimo predittore.
22. Relazione fra matrici di autocorrelazione
e coefficienti AR.
22.1 Premessa.
Esiste una proprieta' che lega l'inverso di una matrice di correlazione [Rxx(k)] ai coefficienti di modelli AR. In pratica, tale via di calcolo della [Rxx(k)] si rivela utile principalmente in due situazioni: quando si deve eseguire simbolicamente il calcolo della inversa della matrice di autocorrelazione; od anche, se i modelli AR sono noti o precedentemente determinati.
22.2 Teoria.
Data la sequenza di autocorrelazione Rxx(k), reale e pari, con k=0..N, vale la seguente relazione:
[Rxx] = LT E L (22.1)
ove il suffisso indica l'operazione di trasposizione di matrice ed in cui le matrici quadrate [Rxx], L, E, di dimensione (N+1)x(N+1), sono definite dalle relazioni seguenti:

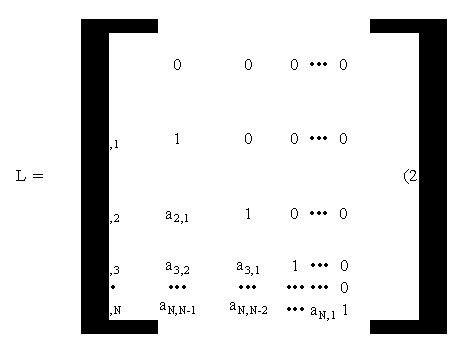
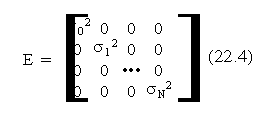
A titolo di esempio, per N=2, si ottiene:


23. Stima spettrale di Capon.
23.1 Teoria.
Il metodo di stima spettrale di Capon calcola lo spettro di densita' di potenza, per una determinata pulsazione w , come la potenza dell'uscita di un filtro accordato in modo ottimale alla pulsazione w . Si ricordi che anche il periodogramma puo' essere visto in questo modo, con filtri con risposta impulsiva del tipo esponenziale complesso di pulsazione w .
Dato un processo stazionario del quale si vuole determinare lo spettro di densita' di potenza, il metodo consiste nel progettare con un criterio ottimale, in funzione della sequenza di autocorrelazione Rxx(k) del processo , un banco di filtri numerici accordati su w con risposta impulsiva a(n;w ) di tipo FIR di ordine N (cioe' con N+1 coefficienti), ovvero:
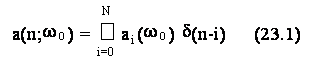
ove i filtri a(n;w ) sono stati scelti, per comodita' di analisi e senza perdita di generalita', con risposte causali. Infatti, eventuali traslazioni temporali delle risposte a(n;w ) non comportano modificazioni nello spettro di densita' di potenza.
Data una generica pulsazione w , detto pertanto
a(w ) = [ a (w ) , a (w ) , ... , aN(w ) ]T (23.2)
il vettore degli N+1 coefficienti del filtro a(n;w ) di ordine N da progettare (un filtro per ogni w ), posto in ingresso al filtro a(n;w ) il processo , deve essere minimizzata la varianza sy (w ) del processo di uscita = data da:
sy (w ) = a(w )H [Rxx] a(w ) (23.3)
ove il suffisso H indica trasposizione e coniugazione mentre:

con il vincolo che il filtro a(n;w ) abbia una risposta in frequenza A(w;w ) (corrispondente alla trasformata di Fourier di a(n;w )) unitaria per w=w , ovvero:
A(w;w ) w=w = A(w ;w ) = e(w )H a(w ) = 1 (23.5)
ove il vettore e(w) e' il vettore definito come:
e(w) = [ 1 , ejw , ... , ejNw ]T (23.6)
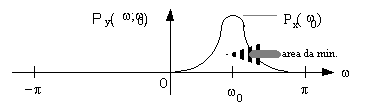
Fig. 23.1. Spettro di densita' di potenza del segnale
in uscita al filtro.
Il motivo di tale minimizzazione con vincolo risiede nel fatto che (vedi Fig. 23.1) occorre minimizzare sy (w ), cioe' l'area sottesa dallo spettro di densita' di potenza del segnale di uscita Py(w;w )=|A(w;w )| Px(w), con il vincolo |A(w ;w )| =1 ovvero Py(w ;w )=Px(w ).
La stima spettrale di Capon Cx(w ) di ordine N (ovvero ottenuta dal progetto di un banco di filtri risonanti FIR ad N+1 coefficienti) del processo risulta essere proprio la varianza di uscita sy (w ) minima rispetto al vettore a(w ) sotto il vincolo (23.5), e cioe':
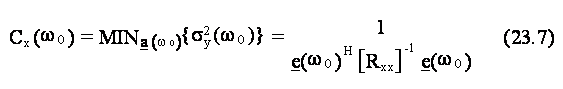
mentre il vettore di coefficienti ottimi aOPT(w ) dei filtri a(n;w ) risulta:
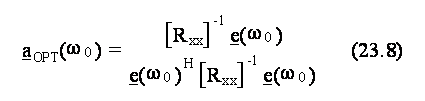
Si noti come il filtro FIR i cui coefficienti sono definiti dalla (23.8) sia in generale complesso. Del resto, gia' la fig. 23.1 mostrava l'effetto di una risposta in frequenza A(w;w ) non simmetrica rispetto all'origine delle frequenze (w= ).
Inoltre, si osservi come, al tendere all'infinito dell'ordine N, le risposte in frequenza dei filtri A(w;w ) tendano per ogni w ad impulsi ideali di altezza unitaria centrati in w=w e, quindi, a trasformatori ideali di Fourier.
Il metodo di Capon ora illustrato si applica per una qualunque pulsazione w ; pertanto le espressioni dell'estimatore spettrale (23.7) e dei coefficienti del filtro (23.8) possono essere equivalentemente esplicitate in funzione della pulsazione complessa w, anziche' della pulsazione complessa w , per una maggiore semplicita' di scrittura.
Infine, e' di notevole importanza teorica ed applicativa la proprieta' che lega l'estimatore spettrale di Capon di ordine N alle stime AR di ordine da 0 fino ad N. Infatti, detta Cx(w) la stima di Capon di ordine N (cioe' con filtri FIR ad N+1 coefficienti) ed Sxi(w) le stime AR di ordine i con 0 i N, si ha:
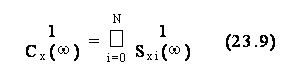
La relazione (23.9) fornisce utili indicazioni sulla risoluzione spettrale del metodo di Capon. Infatti, questo agisce come una sorta di media degli inversi, del tipo parallelo di resistenze, sulle stime AR di ordine da 0 ad N. Pertanto, anche le sue prestazioni risentiranno di questa "mediatura".
In considerazione di cio', l'algoritmo di Capon e' indubbiamente fra i metodi di stima spettrale piu' robusti quando non si hanno indicazioni sull'ordine corretto del modello AR. Tuttavia, proprio per questo effetto di "mediatura", lo stimatore di Capon presenta una minor risoluzione spettrale rispetto al metodo AR di ordine piu' elevato (N), ovviamente nell'ipotesi che l'ordine considerato sia veritiero.
23.2 Esercizio.
Dato il processo stazionario con sequenza di autocorrelazione Rxx(k) data da:
Rxx(k) = -0.062 [d(k+3)+d(k-3)] + 0.125 [d(k+2)+d(k-2)] -
- 0.328 [d(k+1)+d(k-1)] + 0.539 d(k)
determinare lo spettro di Capon di do ordine 2, ovvero ottenibile mediante filtri FIR a 3 coefficienti.
Svolgimento.
Occorre imporre che il vettore
a(w) = [ a (w) , a (w) , a (w) ]T
minimizzi la varianza sy (w) del processo in uscita al filtro FIR con coefficienti a(w), con il vincolo che
e(w)H a(w) = 1
ove
e (w)= [ 1 , ejw , ej2w ]T
Per calcolare la stima spettrale in base alla (23.7) occorre invertire la matrice di correlazione [Rxx], data da:

ottenendo quindi:

Pertanto, sviluppando i conti, si ha:
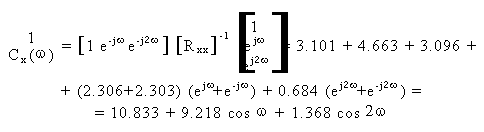
ovvero:
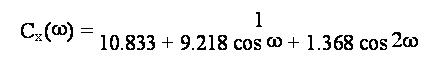
E' da notare che si poteva anche procedere in modo alternativo determinando gli spettri AR di ordine 0, 1, e 2, per poi combinarli in base alla (23.9) per ottenere lo spettro di Capon.
24. Stima spettrale di Pisarenko.
24.1 Teoria.
Il metodo di stima spettrale di Pisarenko (talvolta denominato decomposizione armonica di Pisarenko - PHD) consente di stimare lo spettro di densita' di potenza di processi che si ipotizzano essere costituiti da un numero prefissato di sinusoidi (parte armonica del processo) sovrapposte ad un processo bianco.
Nella versione piu' generale, il metodo richiede la presenza di esponenziali complessi invece di sinusoidi reali. La generalizzazione non prevede sostanziali difficolta' teoriche. Tuttavia, siccome la sua principale applicazione riguarda lo studio di processi reali, nel seguito faremo riferimento a tali processi, sottintendendo che gli esponenziali complessi debbano presentarsi sempre in coppie coniugate.
Il processo bianco puo' essere riguardato come un processo di eccitazione che, similmente a cio' che accadeva nei modelli AR, e' presente all'ingresso di un modello ARMA degenere. Infatti, dato il processo osservato , supposto costituito dalla somma di P sinusoidi (cioe' 2P esponenziali complessi) e da un processo bianco , vale la seguente equazione alle differenze:
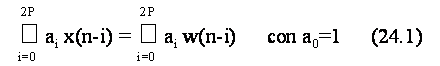
che e' l'equazione di un particolare modello ARMA in cui la parte AR di ordine 2P e' identica alla parte MA sempre di ordine 2P.
Definito il vettore v di dimensione 2P+1:
v = [ v , v , v , ... , v2P ]T (24.2)
e la matrice di autocorrelazione [Rxx], che deriva dalla sequenza di autocorrelazione Rxx(k) del processo per -2P k 2P, come:

l'equazione (24.1) puo' essere risolta in forma chiusa in base alla seguente autoequazione:
[Rxx] v = lMIN v (24.4)
ove lMIN e' l'autovalore minimo della matrice [Rxx] e v l'autovettore ad esso associato.
La stima spettrale di Pisarenko si determina a questo punto imponendo che la varianza s del processo bianco ed i coefficienti dell'eq. (24.1) siano:
s = lMIN (24.5)
ai = vi v per 0 i 2P (24.6)
Una volta trovati la varianza s ed i coefficienti , le 2P pulsazioni (simmetriche a coppia) sono determinate dalle radici dell'equazione:
z2P + a z2P-1 + ... + a2P-1 z + a2P = 0 (24.7)
nel modo seguente:
= (24.8)
Le potenze delle P armoniche reali di pulsazione sono determinabili sfruttando le relazioni seguenti:
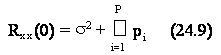
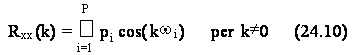
La stima spettrale di Pisarenko Dx(w) del processo , periodica di periodo 2p, risultera' pertanto per w e [-p,p]:
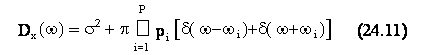
ove d(w-wi) e' l'impulso matematico (delta di Dirac) posizionato in w=wi.
Al contrario del metodo AR, non sono state trovate soluzioni ricorsive per il metodo di Pisarenko. Pertanto, se non e' noto l'ordine 2P del modello, e' necessario rieffettuare i calcoli per ordini successivi (2P+2), arrestandosi quando l'autovalore minimo calcolato non cambia in modo significativo.
Riguardo alla determinazione dell'autovalore minimo, anziche' calcolarli tutti, e' possibile utilizzare procedure numeriche basate sull'equazione v(k)=[Rxx] v(k-1), normalizzando ad ogni passo il vettore v(k) in base alla (24.6) in modo da evitare la divergenza numerica (overflow). La convergenza e' garantita dalla tendenza asintotica verso l'autovalore massimo di [Rxx] (che coincide con quello minimo di [Rxx]) normalizzato ad 1.
Anche il metodo di Pisarenko, come i modelli AR, si basa su rigide ipotesi sulla natura del processo osservato . Il metodo e' assai poco robusto se il processo non e' davvero costuito da un processo armonico e da un processo bianco indipendente additivo.
L'eventuale non rispondenza a tali ipotesi comporta, ovviamente, errori notevoli sulla stima spettrale ottenuta, nel senso che il metodo impone in ogni caso sinusoidi pure (impulsi ideali nel dominio di Fourier) anche se queste fossero smorzate (caso di poli prossimi ma interni al cerchio unitario) o, addirittura, non esistessero del tutto (caso di ordine del modello sovradimensionato).
24.2 Esercizio.
Dato il processo costituito da una sinusoide reale immersa in un segnale casuale bianco, determinare la stima spettrale armonica di Pisarenko basata sulla conoscenza dei seguenti campioni dalla sequenza di autocorrelazione Rxx(k) di :
Rxx(0) = 2 Rxx( 1) = 0 Rxx( 2) = -1
Svolgimento.
Occorre in primo luogo risolvere l'autoequazione (24.4):
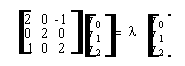
Imponendo det = 0 , si ottiene:
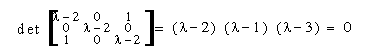
Gli autovalori sono percio' l = 2, 1, 3. Il minimo e' lMIN = s = 1.
L'autovettore v ad esso associato soddisfa l'equazione:
[Rxx] v = lMIN v
pertanto risulta:

ove semplicemente a=v in base alla (24.6).
La polinomiale in z (eq.(24.7)) associata ad a = [ a , a , a ]T e' in questo caso:
z + a z + a = z + 1 =0
le cui radici sono:
z = j
La pulsazione della sinusoide (eq. (24.8)) e' percio':
w = ± p/2
La potenza p della sinusoide e' sovente calcolata in base alla (24.10), che non e' qui utilizzabile in quanto fornisce una soluzione indeterminata. Si utilizza allora la eq. (24.9) per cui:
p = Rxx(0) - s = 2 - 1 = 1
In conclusione, in base alla eq. (24.11), la stima spettrale di Pisarenko Dx(w), periodica di periodo 2p, risulta in [-p,p]:
Dx(w) = 1 + p d(w-p/2) + p d(w+p/2)
che e' illustrata nella fig. 24.1.
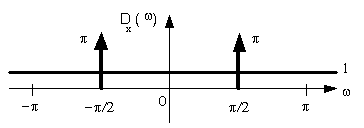
Fig. 24.1. Stima spettrale di Pisarenko del processo .
Parte V. Raccolta di esercizi riepilogativi.
25. Testi di esame di Elaborazione Numerica dei Segnali.
25.1 Esercizio di marzo 1992.
Un processo ha uno spettro di densita' di potenza unitario tra -250 Hz e 250 Hz e nullo al di fuori.
La serie e' ottenuta per campionamento da ogni T=250 ms.
1) Progettare un filtro numerico FIR di lunghezza N=3 per il calcolo della serie costituita dai campioni, presi sempre con passo T, dal segnale:
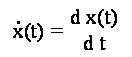
2) Si confronti la risposta in frequenza del filtro progettato con quella del filtro differenziatore (con funzione di trasferimento: 1-z ) e si calcoli l'energia dell'errore delle rispettive risposte impulsive.
25.2 Esercizio del 17 marzo 1992.
(primo esonero)
1) Data l'equazione alle differenze:
y(n) - 3 y(n-1) + 1.76 y(n-2) = x(n) + x(n-2)
1.1) calcolare la risposta impulsiva corrispondente alla soluzione lineare, permanente e stabile;
1.2) calcolare la risposta alla sequenza di ingresso:
x(n) = U(n) (0.5)n
2) Un filtro numerico e' caratterizzato dalla seguente risposta in frequenza:
H(ejw) = 1 - cos w + 0.25 (cos w)
2.1) progettare la struttura del filtro a coefficienti reali sulla base del campionamento in frequenza;
2.2) determinare la risposta del filtro G(z) a fase minima tale che:
| G(ejw) | = | H(ejw) | per ogni w
3) Data la sequenza x(n) avente uno spettro in w pari a X(w), calcolare analiticamente lo spettro Y(w) della sequenza y(n) ottenuta nel seguente modo:
y(2n) = x(n)
y(2n+1) = (-1)n x(n)
25.3 Esercizio di aprile 1992.
Data la risposta in frequenza H(w) di un filtro numerico:
H(w) = |w| per -p w p
1) Calcolare la risposta impulsiva h(n).
2) Calcolare la sequenza trasformata
di Hilbert ![]() (n)
della sequenza h(n).
(n)
della sequenza h(n).
3) Dato il processo stazionario , gaussiano, bianco, di varianza unitaria, calcolare lo spettro dell'errore di predizione di secondo ordine della serie data da:
![]()
25.4 Esercizio del 12 maggio 1992.
(secondo esonero)
Riferendosi a modelli a tempo discreto dei sistemi e dei segnali che transitano in un sistema di comunicazione, un trasmettitore invia al canale un segnale d(n). Il canale, lineare e permanente, e' caratterizzato dalla risposta impulsiva h(n).
Il segnale ricevuto r(n) e' la somma del segnale utile u(n) = d(n) h(n) e di un rumore aleatorio w(n).
Tali segnali sono descritti come segue:
Rw(k) = sw d(k)
Pd(w) = 0.5 (1 - cos w)
h(0) = 1 ; h(1) = 0.5 ; i restanti elementi h(i) = 0.
SNR = 20 log su sw = 18 dB
1) Calcolare lo spettro Pr(w) di .
2) Determinare lo spettro AR di secondo grado di .
3) Progettare un filtro FIR di lunghezza N=3 che consenta la migliore ricostruzione possibile del segnale d(n) a partire dal segnale ricevuto r(n) (un filtro cosi' realizzato e' chiamato equalizzatore di canale).
4) Calcolare il nuovo rapporto segnale/rumore all'uscita del filtro equalizzatore realizzato.
25.5 Esercizio del 15 giugno 1992.
Un processo stazionario e' caratterizzato da uno spettro di densita' di potenza del tipo:
![]()
1) Calcolare la varianza dell'errore di predizione lineare di secondo ordine sui campioni x(nT) presi ogni T=125 ms.
2) Calcolare la varianza dell'errore di predizione lineare di secondo ordine sulla sequenza dei campioni y(n) = x(2nT)
3) Calcolare la varianza dell'errore di predizione su x(nT) nel caso che si utilizzi un'aritmetica a virgola fissa con arrotondamento, usando 8 bit (compreso quello di segno).
25.6 Esercizio del 25 giugno 1992.
1) Disegnare la struttura a coefficienti reali, basata sul campionamento in frequenza, del filtro FIR descritto dalla funzione di trasferimento:
H(z) = (1 - z )
2) Progettare mediante il metodo della trasformata bilineare il filtro caratterizzato dalla seguente risposta in frequenza:
![]()
3) Calcolare lo spettro AR di secondo ordine della serie ottenuta da una serie aleatoria stazionaria, gaussiana, bianca, a varianza unitaria, mediante la trasformazione:
y(n) = [x(n) - x(n-1)]
25.7 Esercizio di luglio 1992.
1) Una sequenza x(n) e' ottenuta dal segnale s(t), limitato in banda tra le frequenze -W e W, come:
x(n) = s(nT).
ove il periodo di campionamento T e':
![]()
Si chiede di progettare un elaboratore numerico per il calcolo della sequenza y(n) definita da:
![]()
2) Un processo armonico del tipo:
a(t) = cos(2p f t + f)
con f uniformemente distribuita in [-p,p], e' contaminato da un rumore gaussiano r(t), di varianza unitaria, bianco nella banda [-W,W] e spettro nullo al di fuori.
Assumendo
![]()
determinare lo spettro di Capon di secondo ordine della serie definita da:
y(n) = [ a(nT) + r(nT) ]
25.8 Esercizio di settembre 1992.
1) progettare il predittore ottimo lineare di secondo ordine per la serie definita da:
![]()
ove w(n) e' una sequenza di rumore bianco di varianza 0.01.
Calcolare la varianza dell'errore di predizione.
2) Calcolare la varianza dell'errore di predizione se il predittore progettato al punto precedente e' applicato alla serie definita da:
![]()
ove v(n) e' una sequenza di rumore di varianza 0.01 con spettro uniforme nell'intervallo [-p/2 , p/2] e nullo al di fuori.
3) Comparare la varianza dell'errore di predizione, ottenuta al punto precedente, con quella che si sarebbe potuta ottenere applicando, invece, il predittore ottimo lineare per .
25.9 Esercizio del 20 ottobre 1992.
Sia y(n) la serie ottenuta per differenziazione (funzione di trasferimento del differenziatore: 1-z ) della serie x(n) caratterizzata dal seguente spettro di densita' di potenza Px(w):
![]()
1) Calcolare lo spettro di densita' di potenza Py(w) di .
2) Determinare lo spettro AR di secondo ordine Py(AR)(w) di .
3) Determinare lo spettro AR di primo ordine Pq(AR)(w) del processo complesso , ove q(n) e' definita come la serie analitica associata a y(n).
4) Confrontare la posizione dei poli nel dominio Z per i due modelli AR determinati ai punti 2) e 3).
25.10 Esercizio del 26 novembre 1992.
1a) Progettare un filtro FIR di lunghezza 4 che approssimi la risposta:
![]()
1b) Disegnare le strutture trasversale ed a campionamento in frequenza (a coefficienti reali) del filtro ottenuto.
2) Calcolare la varianza del rumore di quantizzazione introdotto sull'uscita dalle due strutture, nel caso di aritmetica in virgola fissa con arrotondamento (8 bit + segno).
25.11 Esercizio dell'11 gennaio 1993.
Data la risposta in frequenza H(w), periodica di 2p, che nell'intervallo [-p,p] vale:
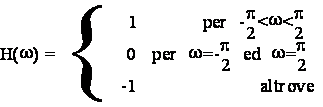
ove w e' la frequenza normalizzata;
1a) progettare il filtro numerico H (z) approssimante la H(w) con il metodo del campionamento in frequenza per N=4;
1b) calcolarne la risposta impulsiva h (n);
1c) graficare qualitativamente il modulo della risposta in frequenza del filtro numerico progettato H (ejw) ;
2a) progettare il filtro numerico H (z) approssimante la H(w) con il metodo della trasformazione bilineare (suggerimento: si parta dal filtro analogico
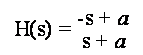
in cui il periodo di campionamento e' T=1 ed a e' una costante opportuna ottenuta imponendo la condizione:
![]()
2b) calcolarne la risposta impulsiva h (n);
2c) graficare qualitativamente il modulo della risposta in frequenza del filtro numerico progettato H (ejw) ;
3a) determinare lo spettro AR del processo in uscita al filtro h (n) quando l'ingresso e' un processo stazionario gaussiano bianco di varianza unitaria;
3b) determinare lo spettro AR del processo in uscita al filtro h (n) quando l'ingresso e' un processo stazionario gaussiano bianco di varianza unitaria.
25.12 Esercizio del 25 febbraio 1993.
Un sistema lineare e permanente a tempo discreto evolve secondo la seguente equazione alle differenze:
y(n+1) = 2.9 y(n) - 2.78 y(n-1) + 0.88 y(n-2) + x(n)
ove x(n) e' l'ingresso ed y(n) e' l'uscita del sistema in esame per un generico istante n.
1) Calcolare la sequenza della risposta impulsiva h(n) corrispondente alla soluzione stabile.
Sia un processo aleatorio stazionario gaussiano con densita' spettrale di potenza Px(w) pari a:
Px(w) = 2 - 2 cos w
2) Calcolare lo spettro di densita' di potenza Py(w) dell'uscita del sistema e la corrispondente sequenza di autocorrelazione Ryy(k).
3) Determinare gli spettri AR del processo di uscita di ordine 1, 2 e 3.
25.13 Esercizio del 16 marzo 1993.
(primo esonero)
1) Data la seguente equazione alle differenze:
y(n+1) = 2.5 y(n) + 1.5 y(n-1) + x(n) + x(n-1)
calcolare la sequenza della risposta impulsiva corrispondente alla soluzione stabile dell'equazione.
2) Sia dato x(t) descritto dalla sua trasformata di Fourier X(f):
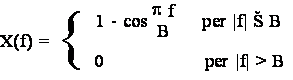
con B = 3 kHz.
a) calcolare le trasformate X (ejw) ed X (ejw) delle sequenze:
x (n) = x(nT )
x (n) = x(nT )
con T = 100 ms e T = 125 ms;
b) indicare uno schema interamente numerico per calcolare la sequenza x (n) a partire dalla sequenza x (n);
c) esprimere X (ejw) in funzione di X (ejw).
3) Progettare un filtro numerico passabasso di tipo Butterworth secondo le seguenti specifiche sul modulo della funzione di trasferimento:
wp (a - 3 dB) = 0.45 rad
ws ( a - 20 dB) = 0.8 rad
25.14 Esercizio del 5 aprile 1993.
1) Un sistema lineare tempo-invariante e' regolato dalla seguente equazione alle differenze:
y(n) = -1.4 y(n-1) + 1.2 y(n-2) + x(n) - 0.5 x(n-1)
All'ingresso e' presente un processo stazionario a media nulla con funzione di autocorrelazione Rxx(k) pari a:
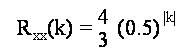
Calcolare la funzione di autocorrelazione Ryy(k) del processo di uscita e determinarne la stima spettrale AR del primo ordine.
2) Data una sequenza x(n) con spettro X(w) che entra in un sistema numerico lineare la cui risposta in frequenza H(w), periodica di 2p nella variabile w, e':
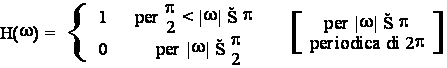
l'uscita y(n) risulta essere ovviamente y(n) = x(n) h(n), ovvero, nel dominio di Fourier, Y(w) = X(w) H(w).
Determinare, in funzione dello spettro X(w), lo spettro D(w) della sequenza d(n) ottenuta per decimazione con fattore F=2 di y(n), cioe' d(n) = y(2n).
3) Data la risposta in frequenza H(w), periodica di 2p, definita al punto precedente, progettare il filtro numerico FIR che la implementa mediante il metodo delle finestre (cioe': antitrasformata di Fourier). (Suggerimento: si tronchi la sequenza della risposta impulsiva h(n) laddove il modulo dei campioni sono minori del 10 % del proprio modulo massimo)
25.15 Esercizio del 18 maggio 1993.
(secondo esonero)
Sia H(z) la funzione di trasferimento in z di un sistema lineare numerico tempo-invariante di tipo FIR:
H(z) = 1 + 0.75 z + 0.5 z
Sia x(n) la sequenza di ingresso al sistema H(z), realizzazione di un processo stazionario gaussiano bianco, di varianza unitaria.
Sia il corrispondente processo in uscita ad H(z).
1) Supponendo di adoperare un'aritmetica in virgola fissa con arrotondamento a 8 bit (cioe': 1 di segno e 7 di modulo), calcolare la varianza del rumore di quantizzazione in uscita al sistema H(z) ed il rapporto segnale/rumore di quantizzazione (cioe' il rapporto tra le potenze di segnale e rumore costituenti ).
Sia Q(z) la funzione di trasferimento in z di un sistema lineare numerico tempo-invariante, posto in cascata ad H(z), di tipo IIR:
![]()
Sia pertanto y(n) la sequenza di ingresso e si denomini v(n) la sequenza di uscita al sistema Q(z).
2) Determinare, usando la recursione di Levinson-Durbin, la stima spettrale AR del processo di primo e secondo ordine.
Sia G(z) la funzione di trasferimento in z di un sistema lineare numerico tempo-invariante di tipo FIR a 3 coefficienti avente come ingresso la sequenza y(n) (cioe' l'uscita del filtro H(z)) e come uscita la sequenza denominata w(n).
3) Progettare il filtro G(z) con il criterio ottimo dei minimi quadrati al fine di invertire il filtro H(z), ovvero in maniera da approssimare in uscita (cioe' mediante la sequenza w(n)) la sequenza di ingresso x(n).
25.16 Esercizio del 31 maggio 1993.
1) Determinare lo spettro AR di secondo ordine della serie x(n) ottenuta filtrando la serie bianca w(n), di varianza unitaria, attraverso il filtro H(z):

2) Una serie aleatoria w(n) gaussiana bianca di varianza unitaria transita attraverso un filtro differenziatore numerico (cioe': x(n)=w(n)-w(n-1)) e, successivamente, attraverso una non linearita' cubica (cioe': y(n) = x (n)).
Valutare la sequenza di intercorrelazione tra l'ingresso w(n) e l'uscita y(n).
3) Valutare la antitrasformata-Z dell'espressione:
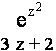
25.17 Esercizio del 21 giugno 1993.
1) Dato il sistema lineare, che evolve in base alla equazione:
y(n) = y(n-1) - 0.16 y(n-2) + 0.16 x(n-1)
avente come ingresso un processo aleatorio bianco, uniformemente distribuito nell'intervallo [-1,1], calcolare la sequenza di autocorrelazione Ryy(k) del processo di uscita .
2) Determinare, per ogni w, la stima spettrale di Capon PyyC(w) del processo prima definito, ottenibile mediante un filtro FIR a 3 coefficienti.
3) Dopo aver determinato le stime spettrali AR di di ordine 0, 1 e 2 (denominate PyyAR (w), PyyAR (w) e PyyAR (w)), verificare che, per ogni frequenza normalizzata w, risulta:
![]()
25.18 Esercizio del 1o luglio 1993.
Sia x(n) una sequenza reale generica; sia a(n) la corrispondente sequenza analitica; sia b(n)=a(2n) la sequenza ottenuta decimando a(n) di un fattore F=2.
1) Determinare lo spettro B(ejw) in funzione dello spettro X(ejw), verificando che non sussiste alcuna perdita di informazione dovuta all'aliasing spettrale.
2) Progettare un dispositivo numerico per ricostruire la sequenza reale originaria x(n) a partire dalla sequenza decimata b(n).
3) Progettare un filtro numerico di tipo FIR per implementare, in forma approssimata, l'operazione di estrazione della sequenza analitica a(n) a partire da una sequenza reale x(n).
25.19 Esercizio del 12 luglio 1993.
1) Data una sequenza x(n) di tipo passa-alto avente come spettro:
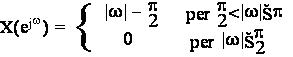
per w e [-p, p] ; al di fuori: periodica di periodo 2p
a) graficare lo spettro Y(ejw) della sequenza decimata y(n)=x(2n);
b) progettare un dispositivo numerico che ricostruisca esattamente x(n) a partire dalla sequenza decimata y(n).
2) Un processo gaussiano reale con spettro di densita' di potenza Px(w)=(1+cosw) e' quantizzato con arrotondamento e rappresentato in virgola fissa con v bit (v-1 di modulo + 1 di segno). Si modelli l'errore di quantizzazione come realizzazione di un processo aleatorio uniformemente distribuito, bianco, incorrelato e additivo nei riguardi del processo con xq(n)=x(n)+e(n).
Determinare l'estimatore ottimo lineare (filtro FIR) a 3 coefficienti con il metodo dei minimi quadrati per ricostruire x(n) a partire dalla sequenza xq(m) nei due casi:
a) v = 2 bit; b) v bit.
25.20 Esercizio del 14 settembre 1993.
Data la risposta in frequenza di un filtro numerico H(w), periodica di periodo 2p, che in [-p,p] vale:
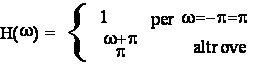
1) progettare un filtro FIR avente 7 coefficienti che approssimi H(w) con il metodo delle finestre (antitrasformata di Fourier);
2) progettare un filtro FIR causale con N=4 che approssimi H(w) con il metodo del campionamento in frequenza;
3) determinare il modello AR del primo ordine di uno dei due filtri numerici realizzati come richiesto nei punti 1) e 2). (suggerimento: si modelli come AR l'uscita del filtro avente in ingresso un processo stazionario bianco di varianza unitaria).
25.21 Esercizio del 15 ottobre 1993.
1) Dato un sistema lineare a tempo discreto invariante alla traslazione definito dalla seguente equazione alle differenze:
y(n) = -1.2 y(n-1) + 1.6 y(n-2) + x(n)
a) determinare analiticamente la risposta s(n) del sistema dato al gradino unitario causale U(n) corrispondente alla soluzione stabile;
b) esprimere la risposta impulsiva h(n) del sistema dato in funzione della risposta al gradino s(n).
2) A partire dalla seguente sequenza binaria a simboli equiprobabili:
0 1 1 0 1 1 0 0 1 1 0 0 1 1 0
a) determinarne la stima spettrale AR di primo e secondo ordine;
b) fornire una predizione, mediante un predittore ottimo (con il criterio del minimo errore quadratico medio) lineare di ordine zero (ZOP) ed uno (FOP), del simbolo binario immediatamente successivo.
25.22 Esercizio del 22 novembre 1993.
Dato un sistema lineare a tempo discreto invariante alla traslazione definito dalla seguente equazione alle differenze:
x(n) = 0.8 x(n-1) + w(n) + 0.5 w(n-1)
1) determinare analiticamente la sequenza di autocorrelazione Rxx(k) del processo di uscita al sistema, quando in ingresso e' presente un processo aleatorio gaussiano bianco a media nulla e varianza unitaria.
Sia inoltre dato il seguente sistema a tempo discreto:
y(n) = x(3n) - 0.8 x(3n-1)
2) determinare analiticamente la sequenza di autocorrelazione Ryy(k) del processo di uscita al sistema, quando in ingresso e' presente lo stesso processo aleatorio definito al passo precedente (corrispondente all'uscita del primo sistema).
3) determinare la stima spettrale AR di primo ordine del processo .
25.23 Esercizio dell'11 gennaio 1994.
Sia un processo ergodico gaussiano bianco di varianza unitaria. Sia il processo ottenuto all'uscita di un sistema invariante alla traslazione definito da:
y(n) = 0.8 y(n-1) + x(n) |x(n)|
Si chiede di determinare:
1) la sequenza di autocorrelazione Ryy(k) dell'uscita;
2) il predittore ottimo lineare (criterio dei minimi quadrati) di ordine zero (ZOP) ed quello di ordine uno (FOP) del processo di uscita ;
3) la varianza e lo spettro di densita' di potenza dell'errore di predizione ottenuto mediante il predittore ZOP determinato al punto precedente.
25.24 Esercizio del 25 gennaio 1994.
Dato il sistema lineare a tempo discreto invariante alla traslazione definito da:
y(n) = 0.4 y(n-1) - 0.68 y(n-2) + x(n) - x(n-1)
ove x(n) e' l'ingresso ed y(n) l'uscita;
1) calcolare la risposta impulsiva h(n) corrispondente alla soluzione stabile;
2) dato un processo di ingresso ergodico gaussiano bianco di varianza unitaria, determinare la sequenza di autocorrelazione Ryy(k) del processo di uscita ;
3) determinare la stima spettrale di Pisarenko del processo di uscita .
25.25 Esercizio del 16 febbraio 1994.
Sia Px(w) lo spettro di densita' di potenza del processo , espresso in funzione della pulsazione normalizzata w:
![]()
Si chiede di determinare:
1) la sequenza di autocorrelazione Rxx(k) del processo ;
2) il predittore ottimo lineare
ad un passo della serie x(n) di ordine zero ![]() e quello di ordine uno
e quello di ordine uno ![]() ,
ottenuti mediante il criterio dei minimi quadrati;
,
ottenuti mediante il criterio dei minimi quadrati;
3) la stima spettrale di Capon ottenibile mediante un filtro FIR a 3 coefficienti.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025