LOGICA FUZZY E GESTIONE DELLA CONOSCENZA

E_(N,S) ---> H

relativamente alla relazione

Se E Allora H con cf = F.

Il meccanismo di inferenza manipolerà e propaganderà eventuali cambiamenti secondo i suggerimenti seguenti:

indagando sull'ipotesi H di una regola raccogliamo delle prove E al fine di confermare o falsificare l'ipotesi.

Indicato con S il fattore di quanto E è sufficiente per H, N dirà quanto E è necessaria per H. Chiaramente se E è vera, quanto maggiore è S tanto più probabile è H. Ovviamente, se E è falsa, quanto minore è N tanto meno probabile è H. Nel caso in cui la probabilità di E stia in mezzo tra il certo e l'impossibile, la probabilità di H è determinata dalla interpolazione tra i casi estremi

1) E è falsa 2) E è vera

I vari cambiamenti definiti dai fattori soggettivi, stabiliti a priori per ogni evento, si propagheranno attraverso la rete da evento a evento, a seconda dei legami esistenti fra di essi e i valori forniti in passi precedenti.

Da quanto detto si evidenzia che un S.E., trattante l'incertezza, manipola l'incertezza relativa al concetto espresso dagli obiettivi nella loro interezza, e non dalle parti che lo costituiscono.

La definizione di limiti tra le parti di due obiettivi relativi ad uno stesso concetto è certamente una grossa carenza, si considerin infatti i seguenti obiettivi:

la pressione è alta

la pressione è quasi bassa

il problema è stabilire quanto il concetto "quasi bassa" può essere considerato simile al concetto "bassa".

(Bratko,I. PROGRAMMING IN PROLOG FOR AI)

Caratteristiche generali dei S.E. Fuzzy.

Per Sistema Esperto Fuzzy intendiamo un S.E. capace di manipolare incertezze relative ad interi obiettivi o proposizioni, imprecisioni relative a sottobiettivi, ed elementi o simboli non imprecisi (crispy).

Risulta quindi chiaro che i S.E. ed i S.E.TRATTANTI L'INCERTEZZA sono nettamente distinti dai S.E.FUZZY visto che i primi sono in grado di rispondere a determinate domande solo con "vero" o "falso", i secondi hanno la possibilità di rispondere a domande con gradi di verità appartenenti all'intervallo [0,1], combinando opportunamente valori probabilistici, mentre gli ultimi trattano possibilità, ovvero gradi di ammissibilità relativi alla percezione soggettiva e non gradi di fiducia rispondendo a domande con gradi di ver 232d33c ità appartenenti all'intervallo [0,1], non solo combinando valori di certezza associati ad ogni regola ma assoggettando tali valori alle incertezze soggettive relative ai termini trattati dal sistema, usufruendo dei tipici formalismi fuzzy.

Un S.E.FUZZY è generalmente un sistema basato su regole che manipolando opportunamente insiemi discreti, numeri e relazioni fuzzy, e servendosi di regole progettate in modo da processare adeguatamente i dati conservati nella base di conoscenza, agisce su una memoria di lavoro e fornisce un output in relazione ad un input di tipo fuzzy.

La memoria di lavoro è un oggetto F_i scelto da F, che può assumere valori definiti in un insieme V_i = (V_i ....V_in), i cui membri possono essere insiemi fuzzy discreti, numeri fuzzy o anche termini crispy, trattati come insiemi fuzzy con grado di appartenenza pari a 1. Con tale organizzazione un S.E.F. non fa alcuna distinzione da un elemento fuzzy e uno non fuzzy.

Analizzando singolarmente ogni parte che lo compone, si può notare che:

ad ogni regola è associato un grado di incertezza cf_rule che misura il grado di appartenenza della regola all'insieme di regole che costituiscono la base di conoscenza.

Per maggiore flessibilità, ogni regola ha la forma:

Se [ ] Q [  ] Q .......Q [ ] allora D

dove [  ] rappresentano patterns e Q connessioni logiche del tipo and, or,

not.

Ogni operando è un attributo di un oggetto con il suo grado di certezza cf uguale ad un valore definito nell'intervallo [0,1], interpretato come il grado con cui un elemento appartiene ad un dato insieme.

Tipicamente un operando è o un insieme fuzzy o un membro di un insieme fuzzy con l'appropriato grado di appartenenza. Un operatore relativo invece può essere o un operatore booleano del tipo ≥,≤, , o una relazione fuzzy Y

Ogni pattern, in tal modo, si può assumere che abbia la forma:

V Y h P

dove

V rappresenta una variabile linguistica che può assumere valori corrispondenti a insiemi fuzzy o valori crispy,

Y una relazione fuzzy,

P un insieme fuzzy o crispy e

h rappresenta un limite linguistico che operando su un insieme fuzzy ne dà in output uno nuovo.

In relazione alla struttura definita sopra e considerando la proposizione fuzzy VYP, ignorando i limiti, se Q è il valore dato in input a V e cf_Q è il fattore di certezza che può essere definito in passi precedenti di computazione, è possibile considerare il valore

K = min(cf_P, cf_Q, Q Y P),

con cf_P il grado di certezza associato a P che può normalmente essere uguale a 1 o minore nel caso in cui P è un membro di un insieme fuzzy definito a livello superiore, e con Q Y P il valore dell'operatore relativo Y applicato a Q e P.

In pratica se Y è un operatore booleano, Q Y P sarà uguale a 1 se Y è vera altrimenti sarà uguale a 0, mentre se Y è una relazione fuzzy, Q Y P rappresenta il valore nato dalla relazione:

numero fuzzy Y numero fuzzy

nel caso in cui Q e P sono numeri fuzzy, mentre Q Y P rappresentail valore nato dalla relazione:

insieme discreto fuzzy Y insieme discreto fuzzy

nel caso in cui Q e P sono insiemi discreti fuzzy.

Chiaramente Y agisce sugli insiemi dipendentemente dal tipo di insieme trattato, cioè se si tratta di numeri fuzzy o di insiemi discreti fuzzy, nel qual caso Y darà il valore di consistenza tra i due insiemi.

[Buckley,J.J.,Siler,W.,Tucher,D. A FUZZY EXPERT SYSTEM. Fuzzy sets and systems 20 (1986) pp.1-16]

LOGICA FUZZY:INSIEMI DISCRETI FUZZY, NUMERI FUZZY E INSIEMI CRISPY.

La scelta di formalismi adatti alla rappresentazione degli elementi caratterizzanti la conoscenza risulta uno dei problemi più forti nella definizione di un Sistema Esperto Fuzzy. Tali elementi avranno caratteristiche di continuità e/o numerabilità, esplicitate dalle funzioni caratteristiche degli insiemi fuzzy ad essi associati, dipendentemente dal campo di applicazione e dall'universo fuzzy considerato.

L'uso di insiemi fuzzy discreti permette una più facile implementazione, però non si ha la possibilità di trattare formalismi adatti ad ogni tipo di conoscenza. La soluzione ottimale la si riscontra nei sistemi ibridi, capaci cioè di gestire sia insiemi di un tipo che di un altro. La struttura che meglio si adatta alle nostre necessità e che meglio risponde ai requisiti di classe e di flessibilità è quella fornita dai numeri fuzzy nel caso di insiemi continui, e quella fornita da insiemi fuzzy numerabili nel caso di insiemi fuzzy discreti.

Quello che cerchiamo è una rappresentazione dei numery fuzzy che elimini o per lo meno riduca le difficoltà che si presenteranno e che permetta di risolvere problemi del tipo:

"Dati due numeri fuzzy M ed N, trovare il grado di possibilità che M sia maggiore (minore)(uguale) ad N".

La classe dei numeri fuzzy presa da noi in considerazione è quella dei FLAT FUZZY NUMBER, dal momento che essa presenta tutti gli aspetti, convenienti e positivi, tipici delle funzioni lineari, proponendo dei meccanismi di sviluppo di operazioni non riscontrabili in altre classi.

LIMITI LINGUISTICI: CARATTERISTICHE E PROPOSTE

La forma normale con cui si presenta una proposizione fuzzy è del tipo

V y eB.

Uno dei punti su cui abbiamo focalizzato la nostra attenzione è stato l'azione del limite linguistico e. Esso può assumere forme del tipo: "molto,poco,abbastanza, più o meno...". Considerando eB come un termine composto dai termini atomici e  e B, il problema si traduce nel determinare il meaning di eB con e modificatore del meaning di B. Secondo Zadeh è possibile definire alcuni operatori di base che permettono di modellare i suddetti limiti.

Un problema che nasce, usando i limiti linguistici, è rappresentato dall'ambiguità che essi possono produrre, nel momento in cui agiscono su un valore linguistico.

"Molto", per esempio, può indicare una crescita di precisione o un cambiamento di classe, dove per classe intendiamo un elemento dell'universo del discorso. L'implicita classificazione dell'universo del discorso in diversi concetti, si ripercuote direttamente sul meaning di ogni concetto. Per esempio, considerando l'universo del discorso approssimativamente diviso in "grandi altezze e piccole altezze", "non grande" può essere identico a "piccolo" e "molto grande" può essere una precisione di "grande". Quando invece, la classificazione è rifinita in "grande", "media" e "piccola"; "non grande" significherà "piccola" o "media". Successivamente se aggiungiamo classi come "molto piccola", "molto grande"; "grande" significherà semplicemente "grande" e non "molto grande" che a sua volta non sarà una precisione di "grande.

Ambiguità semantica.

Da quanto detto, risulta particolarmente difficile associare ad ogni limite una funzione che, assumendo come argomento il grado di appartenenza dell'insieme fuzzy su cui agisce, lo trasformi opportunamente.

Relativamente ai due tipi di insiemi manipolati dal nostro sistema, vogliamo che se l'insieme considerato è un numero fuzzy, il limite lo trasformi in un

numero fuzzy della stessa famiglia, mentre se l'insieme fuzzy è un insieme discreto, vogliamo che tale trasformazione crei un nuovo insieme fuzzy discreto.

In particolar modo considerando una proposizione fuzzy del tipo:

"La velocità di infiltrazione risulta lenta"

con lenta numero trapezoidale rappresentato come:

lenta =[1,5,8,10] (fig.1)

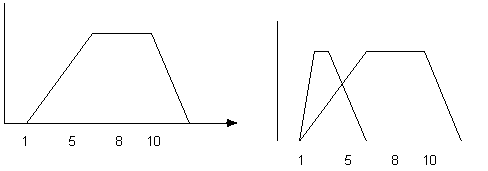
fig.1    fig.2

vogliamo che "molto" trasformi "lenta" in un numero fuzzy dello stesso tipo, caratterizzato cioè da una funzione di appartenenza lineare sia nella parte crescente che in quella decrescente, desideriamo cioè che "molto lento" diventi un nuovo numero fuzzy trapezoidale del tipo:

molto lento=[1,2,4,5] (fig.2)

in modo da poter considerare la proposizione:

"La velocità di infiltrazione risulta molto lenta".

Il problema può essere risolto con una traslazione del "vecchio" numero fuzzy, secondo degli schemi o percezioni soggettive. Ciò chiaramente non ha carattere generale, nel senso che non è possibile definire a priori in che modo traslare. Inoltre bisogna tener presente che molti limiti linguistici hanno un'azione diversa dipendentemente dal significato semantico dell'insieme fuzzy su cui agisce.

Suggerimenti.

Un modo per risolvere i problemi discussi è fornito dall'uso degli operatori di Zadeh, i quali però, effettuano delle trasformazioni radicali sulla funzione di appartenenza dell'insieme su cui agiscono.

Dato per esempio il numero fuzzy A definito come un numero trapezoidale del tipo di fig.3

fig.3    fig.4

"molto" agisce su a in modo tale che, "molto A" è un numero fuzzy non più trapezoidale, cioè un numero del tipo in fig.4

"molto", in pratica, elimina la linearità della parte crescente e decrescente della funzione di appartenenza di A, compromettendo così la flessibilità del sistema.

Un valido contributo, comunque, è dato dalla Truth Functional Modification, una tipica funzione della logica fuzzy, secondo cui:

"Se a è un insieme fuzzy ed e è un modificatore di verità come molto, poco, il risultato della TFM di A usando e, TFM(A/ e), è un insieme fuzzy eA con:

m_eA (x) = m_e m_A(x))"

Possiamo dunque affermare che, scegliendo opportunamente e, otteniamo un risultato che approssimativamente si avvicina a quello proposto.

CONFRONTO TRA DUE INSIEMI FUZZY.

Uno dei problemi da risolvere nel nostro caso è il confronto tra quantità fuzzy e quantità non fuzzy. In pratica indicate con P e Q tali quantità e considerata una relazione fuzzy y, il nostro scopo è quello di ricavare un valore t Œ [0,1] da   P y Q, dove t indica quanto P risulta yQ e P rappresenta un valore che una variabile X può assumere relativamente alla relazione X y Q.

Un esempio tipico è rappresentato dalla proposizione:

"La velocità di infiltrazione risulta lenta"

dove "velocità di infiltrazione" è una variabile linguistica che assume valori come:

"rapida, lenta, moderata, lentissima..."

e "risulta" è una relazione fuzzy che rappresenta l'uguaglianza tea il valore assunto da "velocità di infiltrazione" ed il numero fuzzy "lenta".

Il problema, dunque, consiste nel determinare quanto, per esempio, "lenta risulta moderata".

Confronto tra numeri fuzzy.

Quando si vogliono confrontare due numeri fuzzy, sorgono le seguenti domande:

1)Qual'è il valore di verità del più piccolo o del più grande numero fuzzy in un insieme di numeri fuzzy?

2)Qual'è il valore di verità dell'asserzione

"M ≥ (≤)( ...N"? con M ed N due numeri fuzzy.

Alla prima domanda si può rispondere considerando il max esteso ed il min esteso, cioè il max e il min delle funzioni di appartenenza dei numeri in considerazione.

La seconda domanda, invece, induce alla formalizzazione di alcuni principi che permetteranno di rispondere all'asserzione.

In generale il valore di verità dell'asserzione M≥N è fornito dalla relazione V(M≥N), definita dal principio di estensione come:

V(M≥N) = sup min _X≥Y(m_M(x),m_N(y))

Tale relazione fornisce un grado di possibilità nel senso che quando esiste una coppia (x,y) tale che x≥y e m_M(x)=m_N(y)=1, allora V(M≥N)=1.

CONFRONTO TRA INSIEMI DISCRETI FUZZY.

Vogliamo in questa sezione giustificare la scelta da noi operata tra i vari metodi di confronto.

Il primo problema consiste nella rappresentazione. Si è visto che la più idonea, pur soffrendo delle limitazioni tipiche di una rappresentazione a lista, è quella formalizzata in termini insiemistici, cioè:

S= = [m_S(x_i)/x_i]

dove x_i, elemento i-esimo dell'insieme S, può essere una stringa, un numero reale o un insieme fuzzy regolare, e m_S(x_i) è il grado di appartenenza di x_i a S.

In generale ad ogni elemento non presente nell'insieme S si associa un grado di appartenenza pari a 0.

I metodi di confronto più utilizzati sono le "Misure di similitudini" e gli "Indici di consistenza". Dall'analisi effettuata abbiamo evidenziato che il secondo meglio si presta per le nostre esigenze.

Def. di indice di consistenza.

Siano A e B due insiemi fuzzy, ed X l'universo del discorso, si definisce indice di consistenza tra A e B il valore ottenuto dalla relazione:

C(A,B) = sup _{x X} m_{A B}(x)

In effetti, C(A,B) misura quanto "A è B", cioè il grado di uguaglianza tra A e B, per cui se C(A,B)=0 allora A e B sono distinti, mentre se C(A,B)=1 allora è possibile considerare un elemento x X appartenente sia ad A che a B.

Forniamo un esempi o che giustifica la nostra scelta.

Siano A= e B= due insiemi fuzzy discreti. Per essi C(A,B)=max = 0.3.

Se usiamo invece le misure di similitudini avremo:

S(A,B)=1-max=0.

Si evidenzia dall'esempio che S(A,B) si discosta molto dai risultati desiderati, dal momento che basta che sia m_B(x_i)=1 o m_A(x_i)=1 per dichiarare che B≠A, cosa non vera perchè sia A che B hanno un valore b, con lo stesso grado di appartenenza.

Le stesse considerazioni possono essere fatte se A e B differiscono per solo un valore, evidenziando ancor più il distacco di S(A,B) dai valori desiderati.

INSIEMI CRISPY:NUMERI REALI E STRINGHE

Il termine "crispy" viene assegnato a tutti gli elementi non fuzzy, tali elementi caratterizzano una conoscenza non fuzzy.

Esempio:

"la velocità di infiltrazione risulta 250 mm/h",

250 mm/h è un dato non fuzzy, esso classifica senza indeterminazione la variabile linguistica "velocità di infiltrazione".

Del resto una variabile può assumere sia valori crispy che valori fuzzy.

Possiamo notare che una conoscenza crispy è gestita come una sottoclasse della conoscenza fuzzy. Inoltre è possibile vedere un S.E. come una sottoclasse dei S.E.F.

Bisogna trovare dei formalismi adatti per la rappresentazione di un elemento crispy, sia che esso sia un numero che una stringa crispy.

Numeri crispy.

Un numero crispy è un numero reale definito in un dominio di applicazione.Considerato come un valore a assunto da una variabile linguistica, può essere formalizzato come un numero trapezoidale fuzzy del tipo:

I_a = [a,a,a,a] rappresentato da un generico punto in un sistema di assi cartesiani.

Confidenza a: effetto sui numeri crispy.

Data la proposizione "A risulta I_a con confidenza a " con I_a un numero crispy, è possibile considerare una proposizione ad essa equivalente: "A risulta I_b" con

m_Ib (x) = min (a, m_Ia (x)) +(1-a )   e I_b a,a,a,a].

Limiti linguistici e confronto tra numeri fuzzy e/o crispy.

I limiti linguistici non hanno alcun effetto significativo se operanti sui numeri crispy. In pratica è banale analizzare l'influenza del limite e sul numero I_a dato che se m_e(1)=1 allora m_eIa(x)=1 per ogni x di X, ciò vuol dire che dipendentemente da e, eI_a coinciderà o con I₀=[0,0,0,0] o con I_a a,a,a,a].

E' quindi opportuno considerare eI_a come un numero trapezoidale già presente nella base di conoscenza.

Per il confronto tra numeri fuzzy e/o crispy valgono le considerazioni fatte precedentemente.

Stringhe crispy.

Come per i numeri crispy le stringhe crispy possono essere gestite come insiemi fuzzy, in particolare come insieme fuzzy discreti.

Considerata infatti, la stringa y, essa può essere manipolata come un insieme fuzzy discreto del tipo:

I_y

Per la gestione della confidenza e dei limiti linguistici, è possibile dire che le considerazioni da fare non si discostano da quelle fatte per gli insiemi discreti fuzzy.

CASO DI STUDIO.

(Analisi chimico-fisico del suolo per le attitudini del terreno alla coltivazione: caratteristiche fuzzy).

uno dei problemi fondamentali che l'esperto si pone, per poter definire un terreno idoneo ad una particolare cultura è quello di effettuare una analisi appropiata della morfologia del terreno stesso. Tali analisi basandosi su di un insieme alquanto vasto di informazioni, procede a passo attivando meccanismi che tecnicamente si riscontrano nel tipico formalismo a regola:

Se A allora F con certezza cf

con A ed F proposizioni del tipo: V y t P, e cf il fattore di certezza che gli esperti hanno relativamente alla regola che caratterizza la conoscenza settoriale.

Regole fuzzy che caratterizzano il processo analitico.

Riportiamo di seguito alcune regole che caratterizzano la conoscenza di un esperto nel nostro campo di applicazione.

regola i: se

l'argilla risulta > 40%

e

limo risulta tra il 25% e il 30%

allora

il terreno può essere considerato argilloso.

regola j:    se

l'argilla risulta compresa tra il 15 e il 20%

e

il limo risulta compreso tra il 25 e il 40%

allora

il terreno risulta limoso.

Regole di questo tipo permettono di risalire alla tessitura del terreno, importantissima nella fase iniziale dell'analisi.

Altre regole danno la possibilità di risalire alla valutazione strutturale del terreno stesso, valutazione che permetterà di attivarne delle nuove e di fornire informazioni sulla velocità di infiltrazione. In particolare si ha:

regola s:   se

la struttura del terreno è del tipo lamellare o prismatica

o poliedrica o particellare

allora

la valutazione strutturale risulta cattiva.

Accanto ad esse ne ritroviamo altre che caratterizzano diversi punti dell'analisi: dalla valutazione della velocità di infiltrazione al tipo di azione chimico fisico necessaria per sopperire alle diverse mancanze che si evidenziano nella fase analitica.

Per risolvere il problema dell'incertezza relativa alle diverse argomentazioni presenti nella disciplina stessa, ad ogni regola è stato aggiunto un fattore di certezza relativa alla sicurezza che l'esperto ha di ciò

che ha definito nella regola stessa.

Variabili linguistiche.

Le variabili linguistiche che si riscontrano durante l'analisi assumono valori sia di tipo fuzzy che crispy. In particolare si ha che:

argilla e limo assumono i valori:

">40%", "tra 15 e 20%", "<20%", "tra 1% e 5%", "tra 25% e 30%",

e così via.

"velocità di infiltrazione" assume i valori:

"lenta, lentissima, rapida, moderata,..."

"azione" assume invece i valori:

"sistemazione idraulica, apporto chimico fisico".

Dato il vasto numero di variabili linguistiche e dei valori assunti da esse, abbiamo riportato solo qualche esempio.

Tali valori comunque sono manipolati secondo i formalismi tipici dei numeri fuzzy, degli insiemi discreti fuzzy e degli insiemi crispy.

se per esempio consideriamo i valori che la variabile "velocità di infiltrazione" assume, possiamo notare che essi vengono rappresentati come numeri fuzzy, definiti in base alle esperienze dell'esperto stesso.

In particolare si ha:

lenta=[0.1, 0.25, 2.5, 2.9]

lentissima=[0.010, 0.025, 0.25, 0.29]

moderata=[2, 2.5, 25, 30]

rapida=[20, 25, 254, 260]

Chiaramente non tutti i valori vengono trattati direttamente come insiemi fuzzy, dal momento che alcuni di essi non presentano una indeterminazione netta.

Se consideriamo infatti, un valore che la variabile "struttura" assume, si può notare che "lamellare" risulta ben definito. Esso comunque viene trasformato dal sistema in insieme fuzzy del tipo:

lamellare = [1/lamellare],

con 1 funzione di appartenenza del valore lamellare all'insieme lamellare.

Le stesse considerazioni possono valere per gli altri valori crispy definiti in termini di stringhe, ad esempio:

prismatica, poliedrica, particellare.

Se ad una variabile viene associato un valore numerico, esso per le considerazioni fatte, viene trattato o come un numero fuzzy, relativo al dominio di esistenza associato alla variabile in questione, oppure come un insieme fuzzy discreto il cui unico membro è il numero stesso, considerato come una stringa. Bisogna comunque sottolineare che se una variabile assume valori fuzzy gestiti come insiemi discreti fuzzy i cui membri sono stringhe, ad essa non possiamo associare un valore numerico dal momento che non appartiene ad dominio della variabile stessa.

In pratica se consideriamo la proposizione:

la velocità di infiltrazione risulta lenta

a velocità di infiltrazione possiamo dare un valore come lenta o ancora un valore come 25 mm/h.

Ma se consideriamo la proposizione:

la struttura risulta lamellare,

a struttura non possiamo dare un valore numerico, dato che esso non rappresenta un valore idoneo per struttura che può assumere solo stringhe.

del resto quanto detto risulta possibile per quegli insiemi discreti fuzzy i cui membri non sono stringhe ma numeri reali.

Limiti linguistici.

I limiti linguistici introdotti sono stati trattati in termini di numeri fuzzy,e sono stati rappresentati tenendo presente le trasformazioni più idonee sul termine agente. In particolare quelli maggiormente in uso sono stati:

molto, abbastanza, poco, quasi, circa.

In dettaglio si ha che:

molto = [0, 0.2, 0.8, 1]

poco = [0, 0, 0.5, 1]

abbastanza = [0, 0.4, 0.6, 1]

quasi = [0, 0.5, 0.9, 1]

Processo di inferenza.

Un utente esperto, relativamente alle sue necessità, può chiedere notizie al sistema circa la possibilità di verifica di un certo obiettivo. Il sistema, d'altro canto, combinando opportunamente i vari gradi di certezza relativi a informazioni a lui note, con i valori ttenuti dal confronto di due quantità

fuzzy, darà una risposta del tipo: "esiste una evidenza indicativa [80%] che obiettivo" risulta vero.

In pratica il sistema definisce un confronto tra informazionre e non informazione posseduta e dal confronto nasce una evidenza specialistica sulla veridicità dell'obiettivo.

Se per esempio l'utente vuole avere informazioni circa l'azione da eseguire su un particolare suolo, può formulare una domanda del genere:

l'azione risulta di tipo fisico-chimico?

Il sistema chiedendo all'utente la sua percezione sulla quantità di argilla, limo e sul tipo di struttura, darà la sua valutazione espressa con valori appartenenti a [0,1].

APPENDICE

REGOLE FUZZY

regola_1:  se

argilla risulta '>40%'

e

limo risulta 'tra 25% e 30%'

allora

terreno risulta argilloso

con cf=0.9.

regola_2:  se

argilla risulta 'tra 15% e 20%'

e

limo risulta 'tra 25% e 40%'

allora

terreno risulta limoso

con cf=0.9.

regola_3:  se

argilla risulta '<20%'

e

limo risulta 'tra 30% e 50%'

allora

terreno risulta 'di medio impasto'

con cf=0.9.

regola_4:  se

argilla risulta 'tra 1% e 5%'

e

limo risulta 'tra 8% e 10%'

allora

terreno risulta sabbioso

con cf=0.9.

regola_5:  se

struttura risulta lamellare

o

struttura risulta prismatica

o

struttura risulta poliedrica

o

struttura risulta particellare

allora

'valutazione strutturale' risulta cattiva

con cf=0.9.

regola_6:  se

struttura risulta glomerulare

allora

'valutazione strutturale' risulta buona

con cf=0.9.

regola_7:  se

terreno risulta sabbioso

o

terreno risulta limoso

allora

valutazione risulta cattiva

con cf=0.9.

regola_8:  se

terreno risulta argilloso

e

'valutazione strutturale' risulta buona

allora

'velocità di infiltrazione' risulta lenta

con cf=0.9.

regola_9:  se

terreno risulta argilloso

e

'valutazione strutturale' risulta buona

allora

'velocità di infiltrazione' risulta molto rapida

con cf=0.9.

regola_10: se

'velocità di infiltrazione' risulta molto lenta

allora

azione risulta fisico_chimico

con cf=0.9.

regola_11: se

'velocità di infiltrazione' risulta molto lenta

allora

azione idonea risulta 'sistemazione idraulica'

con cf=0.9.

regola_12: se

'velocità di infiltrazione' risulta molto rapida

e

terreno risulta argilloso

allora

azione idonea risulta 'sistemazione idraulica'

con cf=0.9.