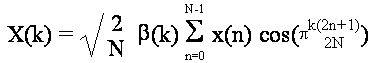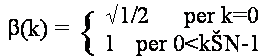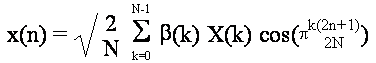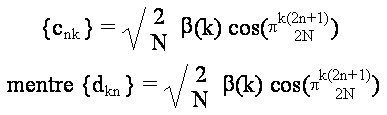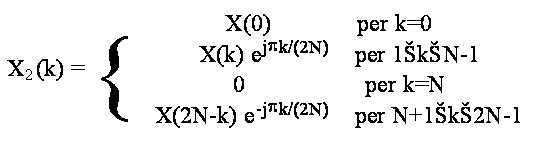Appunti sulla DCT - integrazione dei Lucidi del corso di Elaborazione Numerica dei Segnali

^a edizione: febbraio 2000

disponibile su rete telematica pubblica mediante download gratuito

TRASFORMATA DISCRETA

COSENO (DCT)

. definizione

La trasformata discreta coseno (Discrete Cosine Transform - DCT) di una sequenza x(n) di lunghezza N, e' una sequenza X(k), di lunghezza N, definita dalla:

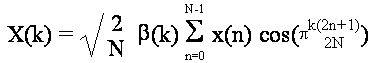
con

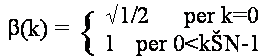
mentre la trasformata discreta inversa coseno (Inversa Discrete Cosine Transform - IDCT) di una sequenza X(k) di lunghezza N, e' una sequenza x(n), di lunghezza N, data da:

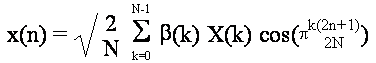
. DCT ed IDCT come sviluppo della sequenza su base ortogonale

Definiti i vettori:

x = [ x(0) , x(1) , ... , x(N-1) ]^T

X = [ X(0) , X(1) , ... , X(N-1) ]^T

e le matrici C e D di dimensione NxN, i cui elementi e , con 0≤n≤N-1 e 0≤k≤N-1, sono:

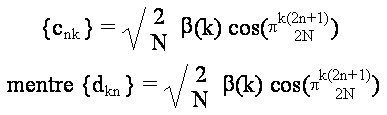
le trasformazioni DCT ed IDCT possono pertanto essere espresse mediante gli operatori lineari C e D=C^-1=C^T come:

X = C x  x = D X = C^-1 X

Poiche' i vettori componenti la matrici C e D sono ortogonali e di modulo unitario, gli operatori corrispondenti sono delle semplici rotazioni di coordinate.

Per tali tali trasformazioni valgono percio' le proprieta' geometriche delle trasformazioni ortonormali (ad esempio, conservazione delle distanze).

. relazione con la DFT

La DFT e' uno sviluppo del segnale su una base di coseni e seni, mentre la DCT e' uno sviluppo su una base di soli coseni.

E' possibile sviluppare un segnale reale in SOLI coseni se e solo se la sua trasformata di Fourier e' reale pura, cioe' se il segnale e' PARI (simmetrico attorno a 0).

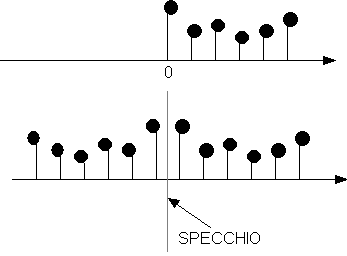
E' possibile sviluppare un segnale QUALUNQUE in serie di soli coseni se il dominio del segnale e' raddoppiato mediante una "specchiatura" attorno a 0 dello stesso segnale:

Nota 1: i campioni originari si sono tutti spostati di mezzo periodo in ritardo.

Nota 2: i campioni specchiati sono in totale in numero doppio di quelli originari.

Partendo da queste due osservazioni, si possono derivare le espressioni della DCT in funzione della DFT e quella della IDCT in funzione della IDFT (che ne consentono un rapido calcolo mediante la FFT diretta ed inversa).

Infatti, definita x (n) la sequenza specchiata centrata in 0:

la DCT X(k) della sequenza x(n) di N campioni coincide numericamente con la DFT X (k) su 2N punti della sequenza specchiata x (n), moltiplicata per un termine di ritardo pari a mezzo periodo di campionamento della sequenza x(n), cioe':

X(k) = e^-jpk/(2N) X (k)

che consente il calcolo veloce della DCT di N campioni mediante algoritmi FFT su 2N punti.

Analogamente, se costruiamo i 2N campioni della trasformata DFT X (k) come:

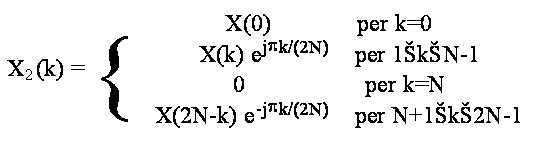
e calcoliamo la IDFT su 2N punti della X(k), otteniamo proprio la stessa sequenza specchiata x (n) centrata in 0, evidenziata in precedenza.

Percio', risulta banalmente:

x(n) = x (n)  per 0≤n≤N-1

che consente il calcolo veloce della IDCT mediante algoritmi FFT inversi (IFFT) su 2N punti.

La validita' della rappresentazione mediante coefficienti DCT consiste nella capacita' di rappresentare in forma compatta

(con pochi bit) i coefficienti dello sviluppo.

In altre parole, benche' l'energia totale dei coefficienti di sviluppo fra le diverse basi che possono essere usate per rappresentare i segnali DEVE ESSERE UGUALE per trasformazioni ortonormali, l'energia media dei coefficienti DCT risulta assai spesso la piu' "sbilanciata", essendo maggiore l'entita' dei primi coefficienti (basse frequenze) e minore quella degli ultimi (alte frequenze).

Questa proprieta' consente di quantizzare fortemente (riducendo cosi' il numero di bit adoperato) molti dei coefficienti DCT, arrivando persino ad ometterli nella trasmissione (costo in bit praticamente nullo) se sono molto piccoli.

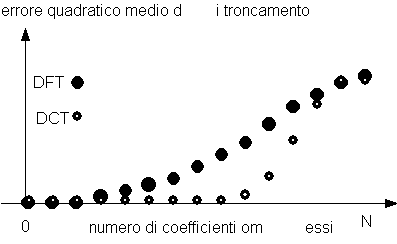
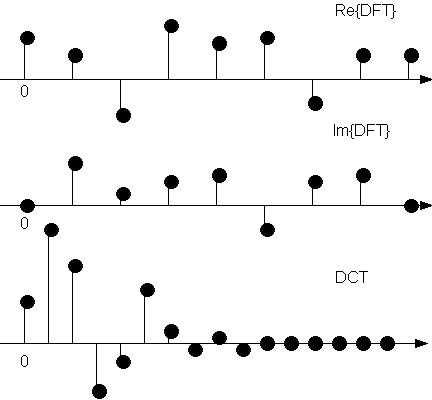
Se, ad esempio, si decidesse di trasmettere solo meta' o un quarto dei coefficienti, l'errore di troncamento sarebbe praticamente insignificante per la DCT, mentre assai piu'

rilevante per la DFT.

Si noti come l'energia dell'errore e' identica per 0 ed N coefficienti omessi in entrambi i casi di utilizzo della DFT e della DCT. Infatti entrambe costuiscono basi complete per la rappresentazione di segnali o immagini.

Diversa e' invece l'efficienza di rappresentazione se si considera soltanto un sotto-insieme di coefficienti di sviluppo. Infatti, molti coefficienti DCT possono essere quantizzati a zero e quindi omessi nella trasmissione, risparmiando cosi' una notevole quantita' di bit.

La proprieta' di compattazione dell'energia della DCT e' sfruttata nei modermi metodi per trasmissione o memorizzazione di immagini (standard JPEG per le immagini fisse e fotografiche ed MPEG per le video-sequenze), usate nelle reti internet, nelle telecomunicazioni televisive digitali e nei CD-ROM.

A titolo di esempio, e' mostrata l'immagine del docente del corso codificata mediante la tecnica JPEG, che utilizza la DCT bi-dimensionale di blocchi 8x8 pixels.

Nelle immagini mostrate, sono stati utilizzati diversi livelli di quantizzazione dei coefficienti DCT, dal piu' grossolano ed economico, fino al piu' raffinato e costoso (costo della codifica, da sinistra a destra: 0.86, 1.16, 1.59, 2.11, 2.89, 7.75 bits/pixel).