Il moto armonico semplice

fisica

Il moto armonico semplice

Il moto armonico semplice è la proiezione di un moto circolare sul diametro della circonferenza, è un moto periodico sinusoidale unidimensionale, caratterizzato da due costanti PULSAZIONE e AMPIEZZA o SPOSTAMENTO. La velocità e l'acceleraz 929j98j ione si possono ricavare proiettando i corrispettivi vettori sul diametro. Siamo in presenza di un moto armonico semplice o M.A.S. nel caso in cui l'accelerazione sia proporzionale ed opposta allo spostamento.

Periodo T=1/f = ω/2π s

Frequenza f = 2π/ω Hz (1 Hertz = 1 oscillazione al secondo)

Pulsazione ω = 2πv rad/s

Legge oraria  x(t) = r cos(ωt)

v(t) = - ωr sen(ωt)

a(t) = - r cos( t)

v_max= ωr

A = Ampiezza, massima elongazione

a_max = - ω²r

in queste formule "r" può essere sostituito da "A".

Le forze elastiche producono questo moto e seguono la legge di Hook

F = -kx   -kx = ma a = (-k/m)x ω =√(k/m)

a = - ω²r

Il M.A.S. è il movimento di una particella di massa m soggetta ad una forza proporzionale allo spostamento della particella, ma di segno opposto.

IL PENDOLO DI GALILEO è un oscillatore armonico se è fatto oscillare per piccole ampiezze.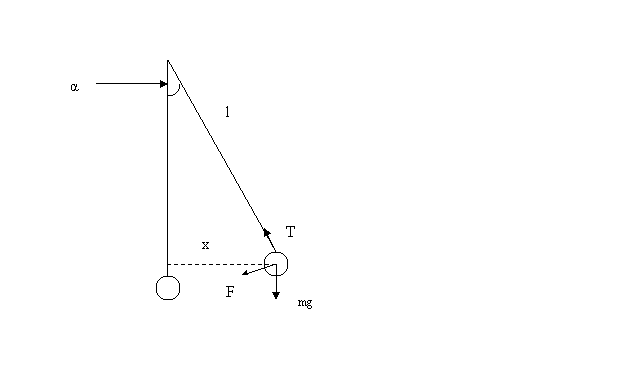

F = mg sen F = -mg(x/l) -mg(x/l ma a = (-g/l)x =√(g/l)

X =l sen

sen = x/l

Più si allontana la pallina dall'asse più diventa grande la forza.

T = 2π√(l/g)    T² = (4 π²/g) l

L'energia potenziale di un oscillatore elastico è interamente associata alla  molla invece quella cinetica al blocco. L'energia del sistema è l' E_tot= E_el + E_k

E_tot= ½ k x² + ½ mv² sostituisco a x e a v le equazione trovate inizialmente ed otterrò E_tot= ½ kA²

Si ha risonanza solo quando ω = Ω

allora la forza F(t) di un oscillatore elastico varrà: F₀ cos(Ωt)

_{frequenza oscillazione esterna}

forza massima

ΣF = ma

F₀ cos(Ωt) - kA cos(Ωt) = m (-Ω²A cos(Ωt))

kA-m A = F₀

A = (F₀/m)/(km/m ) = (F₀/m)/(

Quando la funzione A tende ad infinito l'oscillazione diventa anarmonica e non vale più la legge di Hook infatti intervengono attriti che fanno fare una cupola al grafico. Due pesi legati a tre molle si possono muovere secondo due fasi: tutti e due OSCILLAZIONE DI FASE in cui la molla centrale non compie lavoro e l'altra chiamata POSIZIONE DI FASE in cui tutte le molle si muovono e quindi nel grafico avrò due picchi. Nel caso della risonanza l'energia deve essere ricalcolata scambiando nelle formule di prima ω con Ω.