Grandezze fondamentali

fisica

Grandezze fondamentali

Queste non sono riconducibili ad altre, che anzi, vengono a formarsi proprio a partire da queste, o meglio dalle loro operazioni interazioni a livello delle operazioni fondamentali.

Le grandezze fondamentali sono rappresentate nel S.I. , al quale bisogna solitamente fare riferimento nelle indicazioni dell'unità di misura.

Se non ci riferisce nel S.I bisogna quantomeno avere l'accortezza di utilizzare un solo tipo di sistema, evitando le indicazioni miste, a seguito delle quali si rischia di pervenire ad un risultato errato.

Alcune variabili fisiche non appartenenti alle sette fondamentali pur essendo da esse definite vengono nominate autonomamente:

es: forza = kg*m*s^-2= N

lavoro=m²*s^-2=j

queste due variabili vengono considerate appartenenti al S.I. in quanto definite da grandezze ad esso appartenenti

Alcune unità di misura sono correntemente utilizzate al posto di quelle del S.I. per motivi di comodità di calcolo, quando si tratta di numeri a seconda molto inferiori o superiori all'unità di misura più corretta.

In questi casi per usare le formule è necessario servirsi dei fattori di 515f58f conversione.

Errori di misura

L'errore in una misurazione dipende dal mezzo utilizzato per effettuarla.

Per separare la parte veramente nota di una misura dal suo ordine di grandezza mediante la notazione scientifica.

Es: 1500 kg sensibilità 0,1kg 4 cifre significative

150*10¹ sensibilità 1kg 3 cifre significative

l'errore viene segnalato ponendo l'incertezza della misura a seguito della stessa, preceduto dal segno +/-, a intendere il valore dell'incertezza sia in eccesso che in difetto.

Per operare al meglio con l'errore assoluto è necessario studiare il suo comportamento nell'ambito delle principali operazioni

Somma algebrica: si opera la somma tra i valori assoluti degli errori di tutti termini sommati

DG=Dx+Dy

Prodotto e divisione: si opera la somma degli errori relativi dei due termini, ottenendo l'errore relativo del risultato, che andrà in seguito convertito in assoluto moltiplicandolo per il valore del risultato dell'operazione

= +

es: S= (80,2 +/-0,2)*(120,1+/-0,2)= 9632,02

S=9600+/-40 la variazione del valore di S dipende dal fattore che l'errore fiale della misura incide sulle cifre significative. In effetti per essere precisi il computo delle cifre significative del numero dovrebbe esse 96*10²

Cifre significative

0,23 : 2 cifre significative

: 5 cifre significative

Nelle somme algebriche, come nelle divisioni e nei prodotti, si privilegia il numero di cifre significate del valore meno preciso. Quindi se abbiamo tre valori rispettivamente con 1, 2 e 3 cifre significative, il risultato dovrà essere riportato con cifre significative in numero eguale al valore più incerto, ovvero in questo caso, con 1 cifra.

Nel caso di utilizzo di formule complesse è consentito, anzi consigliato, di mantenere il maggior numero di cifre durante tutto l'operazione di calcolo, per poi operare normalmente al momento della definizione del risultato finale.

Calcoli approssimati

Si sfruttano gli ordini di grandezza non per avere un risultato preciso, ma per avere un idea dell'esattezza del risultato ottenuto.

Es: si afferma che la massa della terra, il cui valore reale è di 5,98*10²⁴ kg, sia quasi uguale a 10 mol di kg. Considerando che 10 mol di kg equivalgono a 6*10²⁴ kg, possiamo affermare che, pur non essendo i due valori perfettamente coincidenti, l'affermazione può essere considerata valida dal punto di vista dell'ordine di grandezza.

In sintesi: ordine di grandezza: da un idea del risultato al quale si dovrà pervenire

Cifre significative: permettono di definire l'esatto risultato di un calcolo e il conseguente errore

Coordinate polari

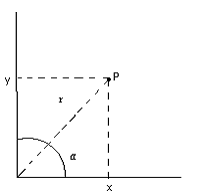Oltre alle normali coordinate ortogonali, è possibile utilizzare diversi tipi di metodologie mirate al ritrovamento dei punti sul piano cartesiano; a fianco delle coordinate sferiche,che non tratteremo,vediamo le coordinate polari, che tengono conto della distanza del unto dall'origine degli assi e dell'angolo formato dalla retta passante per P e per l'origine con l'asse delle x.

Conversione di coordinate:

______

r= (x²+y²) y= r*sena

a=arc^-1x/y  x= r*cosa

es:    (2;1) = (

GRANDEZZE VETTORIALI E SCALARI

scalari: necessitano soltanto del valore numero di intensità per essere definite

vettoriali: necessitano, oltre al valore numerico di intensità, anche di informazioni aggiuntive, quali verso e direzione

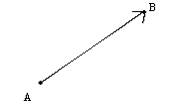
modulo: valore numerico della distanza tra A e B

verso: orientazione del vettore nello spazio

direzione: la retta su cui il vettore giace

Due vettori sono considerati uguali quando sono paralleli ed hanno modulo e verso coincidenti.

Operazioni con grandezze vettoriali

Si tratta di operazioni di origine grafica,anche si in alcuni casi la componente grafica viene tralasciata, grazie all'uso di formule matematiche da essa derivate.

Somma

primo metodo

sovrapposizione delle estremità vettoriali di partenza con conseguente costruzione del parallelogramma. La diagonale della figura geometrica disegnata sarà il vettore risultante della somma.

Ovviamente si possono sommare soltanto grandezze vettoriali caratterizzate dalla stessa unità di misura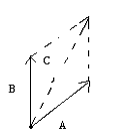

nel caso di somma di più vettori si collegano le estremità dei vettori in manieria ce questi siano ordinati in maniera testa-coda. Il vettore somma sarà dato dal vettore che collega la coda del primo vettore con la testa dell'ultimo.

_ _ _ _ _ _

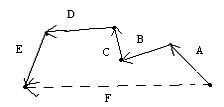
A+B+C+D+E=F

secondo metodo

si tratta di un metodo cartesiano, che tiene conto delle coordinate spaziali e/o polari dei punti che definiscono i vettori.

Per definire il verso dei vettori invece di usare x, y e z useremo i loro equivalenti vettoriali, i cosiddetti versori, ce ci danno un'idea del verso dei vettori

i→ asse x

j→ asse y

k→asse z

Operiamo ponendo le origini dei vettori da sommare sull'rigine degli assi, in modo che coincidano.

Una volta conosciuti i valori delle coordinate ortogonali dei puntiche definiscono i vettori non è difficile operare la loro somma.

_

I valori Rx ed Ry, ossia le componenti utili di R, sono definiti rispettivamente come:

Rx = Ax-Bx

Ry = Ay-By

con questi dati, considerando che il vettore si origina all'origine degli assi, possiamo trovare il valore del modulo mediante

_ __________

|R| = √(Rx)²+(Ry)²

L'angolo formato dal vettore con l'asse x è dato dalla formula

α= tg^-1 y/x

es: vettore A Ax= -25 u.a. (unità arbitrale)

Ay= 40 u.a.

_ _________

|A| = √(-25)²+40² = 47,2 u.a.

α= tg^-140/-25 = -58

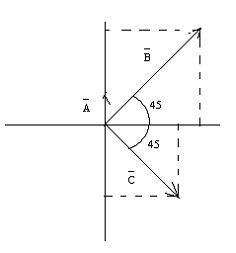es 2:

_

|A| = 20 u.a.

_

|B| = 40u.a.

_

|C| = 30 u.a.

A = Aj = 20 u.a.

_ _

B = Bi + Bj Bi= |B|*cosα = Bj = |B|*senα = 28,3 u.a.

_

C = Ci + Cj Ci = |C|*cosα = 21,2 u.a.

_

Cj = |C|*senα= -21,2 u.a.

Rx= Ax+Bx+Cx= 49,5 u.a.

Ry=Ay+By+Cy= 27,10u.a.

_ __________

|R| =

a= tg Ry/Rx= 31,88

Come possiamo vedere, pur usando un sistema di riferimento cartesiano, possiamo tranquillamente

operare i nostri calcoli senza il bisogno di disegnare i vettori; basta conoscere i dati relativi alle loro coordinate spaziali.

Prodotto

se si parla del prodotto tra di una misura scalare ed una vettoriale, sapremo che il risultato sarà sempre una misura vettoriale, di uguale verso ma diverso modulo. Si può dire che lamisura scalare ce moltiplica il vettore agisca da intensificatore.

Nel caso di prodotto tra due vettori possiamo distinguere due casi. Formamente si separano per l'uso del segno di moltiplicazione * e di X

Prodotto scalare

Primo metodo

Tiene conto del modulo dei vettori, infatti prevede di considerare la risultante dell'uno sull'altro nel fare il prodotto. Per questo la sua formula di base è la seguente

_ _ _ _

A*B = |A|*|B|*cosα

Gode della proprietà commutativa, e nn tiene in considerazione il verso.

Secondo

Un altro metodo di calcolo consiste, ipotizzando di far coincidere le code dei vettori con l'orgine degli assi, nel prodotto delle coordinate spaziali che definiscono i vettori.

In questo caso,dato che nn si tiene conto del verso i versori avranno le seguenti caratteristiche moltiplicative

i*i=1

j*j=1

k*k=1

i*j=0

A = Ai*Aj*Ak

B= Bi*Bj*Bk

A*B= =AxBx(ii)+AxBy(ij)+AxBz(ik)+AyBx(ji)+AyBy(jj)+AyBz(jk)+AzBx(ki)+AzBy(zj)+AzBz(kk)=

= AxBx+AyBy+AzBz

Di consegeunza i valori i,j e k del nuovo vettore,con iquali potremo definirlo nello spazio sn i seguenti

Prodotto vettoriale

In questo caso si tiene conto del verso del vettore prodotto, e pertanto non gode della proprietà commutativa.

Primo metodo

_ _ _ _ _

AxB = C di cui modulo = |A|*|B|*senα

verso= ortogonale ad A ( primo vettore del prodotto) e giaciente sullo stesso piano

Per avere un'idea del verso si usa la regola della mano destra, ponendo il pollice come primo vettore e l'indice come l'altro. Il medio sarà il verso del vettore prodotto

Secondo metodo

Anche qui si tiene conto delle coordinate spaziali che caratterizzano i vettori, ma qui i versori hanno comportamento diverso, rendendo più difficile la formula.

i*i=0

i*j=k

j*k=i

k*i=j

j*i=-k

Quindi

A = Ai*Aj*Ak

B= Bi*Bj*Bk

A*B= =AxBx(ii)+AxBy(ij)+AxBz(ik)+AyBx(ji)+AyBy(jj)+AyBz(jk)+AzBx(ki)+AzBy(zj)+AzBz(kk)=

i= (AyBz-AzBy)

j=AzBx-AxBz

k=AxBy-AyBx

es:

._

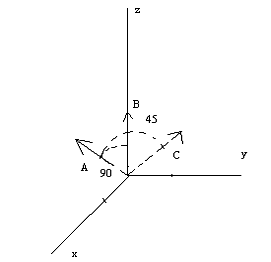
|A| = 1,8 u.a.

._

|B| = 1,2 u.a.

_ _

A*B= 0 xchè l'angolo tra A e B = 90

_ _ _

AxB=C

._ _ _

|C|= |A|*|B|*senα= 2,16 u.a. xchè sen90 = 0

DIVERSI TIPI DI FORZE

FORZA-------- di campo: avviene senza contatto (campo elettrico, gravità, forza nucleare)    di contatto: forza vettoriale che necessita di vero e proprio contatto fisico

legge d'inerzia: un corpo rimane in quiete fintanto che su di esso non agiscono forze esterne

Diversi tipi di forze:

S_i F_i

a = ^_______ se a=0 allora F=0

m_i

mt*m

Fg = mg = G* ^_________

r²

1

Fe= ^_______

4pe₀

_

F_elastica = -kx

_

F_{attrito =} -bv

es.

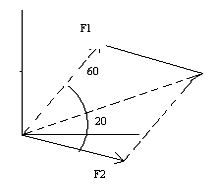
m= 0,3kg

._

|F1| = 5N

. _

|F2| = 8N

a = ?

F1x = 5cos60 = 4 F2x = 8cos20 = 7,5

F1y = 5sen60 = 4,83 F2y = 8sen20 = 2,73

Frx= 11,5 ax= Frx/m= 38,33m/s²

Fry= 7,6 ay= Fry/m= 25,33m/s²

_ ____________

|a|= m/s²

Potenza e quantità di moto

Potenza

Tiene conto del tempo in cui una forza si esprime. Minore è il tempo in cui una forza si esprime, maggiore sarà la potenza prodotta.

dL

P= ^_____ quando t tende a zero. Altrimenti si tratta di una normale variazione(delta)

dt

Dimensioni fisiche (ossia le variabili espresse con le grandezze fondamentali)= mx²

^______

t³

La potenza si misura in j/s = W

Tenendo conto delle dimensioni fisiche della potenza,possiamo strapolare una seconda definizione, basata questa volta sulla forza.

dL   ds _{__}

Se P= ^______ e dL = F*ds P = F ^_______ = F*v

dt  dt

es: m=70kg

h=3m

t=2s

dL=?

P=?

Si tratta di lavoro contro gravità, quindi

dL= mgh= 70kg*9,8m/s*3m=2,1*10³j

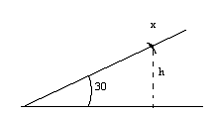
es 2: m=700kg

P=800W

v=?

dL= mgh h=x*sen30 dL= mgx*sen30

mgx*sen30 P

P= ^{_______________} = mgv*sen30 v= ^____________ = 800W/700kg*sin30= 0,23m/s

t    mg*sen30

Quantità di moto

Esprime matematicamente la forza dell'interazione fra due corpi, presa in relazione con la loro velocità

_

p = m*v

La variazione di p nel tempo, ossia dp, è una grandezza detta impulso e definisce la forza impressa ad un corpo nell'intervallo d tempo. Oltre che dalla differenza della quantità di moto iniziali e finali del sistema, può essere dato dall'equazione

_ _

dp = dF*dt

La caratteristica principale della quantità di moto è la sua conservazione nel tempo, allo stesso modo di quanto accade per l'energia.

Perchè questo risulti esatto è necessario lavorare in un sistema isolato, in modo che non vi siano forze agenti dall'esterno ad eccezione di quelle prese in considerazione nell'analisi (es: attrito)

es: m=0,15kg

v=40m/s → v

v₁=50m/s ← v₁

dt=2*10^-3

dp=?

<F>=?

p= 0,15kg*40m/s=

p₁= 0,15*50m/s=

dp= p-p₁= (mv)-(-mv₁) = 13,5N*s

Il segno negativo di mv₁ si spiega i quanto si presume che le due forze abbiano verso opposto.

<F>= dp/dt= 13,5N/s / 2*10^-3s= 6750 N

FORZE NEI CORPI NON PUNTIFORMI

Nei corpi puntiformi la traslazione avviene nello stesso verso della forza applicata

Nei corpi legati, o corpi estesi, la traslazione è dipendente da punto in cui la forza viene applicata. Dobiamo quindi tenere conto di molte più varabili.

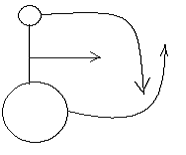
Come ci si rende conto dal disegno, imponendo la forza i un qualsiasi punto, il corpo esteso perverrà ad un moto circolare, a meno che la forzan sia impressa in un puntopreciso.

Definizioni utili

applicando la forza nel c.m. (centro di massa o baricentro) il corpo esteso si comporta come se fosse puntiforme, traslando nella stessa direzione della forza applicata

sul grafico cartesiano l' r_cm si trova con la seguente formula

m₁x₁+m₂x₂

c.m. = ^{________________}

m₁+m₂

Nel caso di corpi simmetrici, il c.m. Si trova lungo l'asse di simmetria

N.B.: nn è detto che c.m. coincida con il centro gravità

applicando la forza al di fuori di c.m. Il corpo andrà incontro ad un moto rotatorio. Dovremo quindi imparare nuovi modi per definire la sua velocità

velocità angolare: misura i radianti percorsi nell'intervallo di tempo

2π

ω = ^______

t

essendo gli angoli non definiti dal alcuna grandezza, le dimensioni fisiche della velocità angolare saranno espresse da t^-1

velocità tangenziale: prodotto della velocità angolare per la distanza dell'applicazione della forza dal c.m.

_ _

|v_t| = ω*|r|

accelerazione tangenziale:

a_t = (d ω /dt)*r

accelerazione centripeta

a_c = r* ω ²

momento d'inerzia

I = m*r

momento della forza:

_ _

î = r x F

oppure, tenendo conto che

F = m*a e a = (d ω /dt)*r e m*r = I e d ω /dt = α

î = m*r*a = m*r²* d /dt

î = I*α

momento angolare:

_ _ _ _ _

L = |r|*m*v = |r|*m*ω*|r| = I* v_t

Sintesi e confronto

Nella tabella a seguito possiamo notare le analogie tra i comportamenti dei corpi puntiformi e di quelli estesi