|
|
| |
Il pianeta più vicino al sole è Mercurio, cui seguono Venere, la Terra, Marte, la fascia degli asteroidi, Giove, Saturno, Urano, Nettuno e Plutone. Gli antichi conoscevano solo 5 pianeti, oltre alla Terra. Urano fu scoperto nel 1781 e Nettuno nel 1846 sulla base di perturbazioni gravitazionali dell'orbita di Urano. Lo stesso accadde nel 1930 per Plutone, la cui esistenza fu ipotizzata per spiegare alcune irregolarità nell'orbita di Nettuno. Il sistema planetario presenta forti regolarità e simmetrie che ci inducono a considerare l'ipotesi di un'origine comune del sole e dei pianeti. Se infatti i pianeti fossero degli intrusi casualmente catturati dal campo gravitazionale del sole essi non presenterebbero le seguenti regolarità:
a) tutti i pianeti si muovono intorno al sole nello stesso verso antiorario, se osservati dal polo nord celeste. Tale verso risulta concorde con il movimento di rotazione del sole intorno al suo asse.
b) le orbite dei pianeti giacciono tutte sullo stesso piano o quasi. Fa eccezione Plutone che risulta inclinato di 17° rispetto al piano dell'orbita terrestre (eclittica). Questa ed altre anomalie di Plutone fanno d'altra parte ritenere che esso abbia avuto una genesi diversa rispetto agli altri pianeti. Alcuni sostengono ad esempio che si tratti di un ex satellite di Urano entrato in orbita intorno al sole.
c) i moti di rotazione dei pianeti intorno al loro asse sono tutti concordi e antiorari se osservati dal polo nord celeste. Fanno eccezione Plutone e Venere che presentano un moto di rotazione orario o retrogrado.
d) le distanze dei pianeti dal sole seguono una legge empirica, che rimane peraltro ancor oggi misteriosa, scoperta nel 1766 da Tietz (Titius) e successivamente divulgata da Bode. Espressa in termini moderni, con le distanze medie dei pianeti dal sole (R) misurate in unità astronomiche, la legge di Titius e Bode prende la seguente forma:
R = 0,4 + 0,3 (2n
con n che può assumere i valori - (meno infinito), 0, 1, 2, 3.......
con n = - R = 0,4 U.A. (Mercurio)
con n = 0 R = 0,7 U.A. (Venere)
con n = 1 R = 1 U.A. (Terra)
etc
I valori così ottenuti si approssimano in modo piuttosto soddisfacente alle distanze reali, con l'eccezione dei pianeti più esterni. E' inoltre interessante notare che fino a tutto il '700, la legge di Titius e Bode mostrava un 'buco' per n = 3, prevedendo in tale posizione la presenza di un pianeta tra Marte e Giove.
La lacuna fu colmata nel 1801 quando l'astronomo italiano Piazzi scoprì in quella posizione il più grande degli asteroidi, Cerere.
e) i pianeti possono essere suddivisi in due grandi gruppi omogenei per quanto riguarda le proprietà fisiche e chimiche, se si esclude ancora una volta Plutone. I 4 pianeti terrestri (Mercurio, Venere, Terra, Marte) ed i 4 pianeti gioviani (Giove, Saturno, Urano, Nettuno).
I pianeti terrestri presentano dimensioni relativamente piccole, ma, essendo costituiti di materiali prevalentemente silicatici (rocciosi), hanno densità elevate (4 - 5,5 kg/dm ). Presentano pochi o nessun satellite e le loro velocità di rotazione sono piuttosto basse.
I pianeti gioviani sono di grandi dimensioni (pianeti giganti), ma essendo composti essenzialmente di elementi chimici leggeri, prevalentemente Idrogeno, presentano densità molto basse, in alcuni casi (Saturno) addirittura inferiori a quella dell'acqua. Presentano in genere un elevato numero di satelliti ed elevate velocità di rotazione intorno al loro asse (10 - 15 ore).
|
|
Mercurio |
Venere |
Terra |
Marte |
Giove |
Saturno |
Urano |
Nettuno |
Plutone |
|
Dist Media Sole (UA) semiasse maggiore a (106 km) |
|
|
|
|
|
|
|
|
|
|
(1) Eccentricità e |
|
|
|
|
|
|
|
|
|
|
(1) Perielio (UA) (106 km) |
|
|
|
|
|
|
|
|
|
|
(1) Afelio (UA) (106 km) |
|
|
|
|
|
|
|
|
|
|
Dist. Min. Terra (UA) (106 km) |
|
|
|
|
|
|
|
|
|
|
Dist. Max. Terra (UA) (106 km) |
|
|
|
|
|
|
|
|
|
|
(2) Per. rivol. sidereo (giorni) (anni) |
|
|
|
|
|
|
|
|
|
|
(2) Vel. Rivol. media (km/s) |
|
|
|
|
|
|
|
|
|
|
(3) Periodo riv. sinodico (giorni) |
|
|
|
|
|
|
|
|
|
|
(4) Periodo rotaz. sid (ore) (giorni) |
|
|
|
|
|
|
|
|
|
|
(4) Incl asse su orb (gradi) |
|
|
|
|
|
|
|
|
|
|
(5) Diam App min/max (sec arco) |
|
|
|
|
|
|
|
|
|
|
Inclinaz. Orbita su eclitt (gradi) |
|
|
|
|
|
|
|
|
|
|
Numero satelliti |
|
|
|
|
|
|
|
|
|
|
(6) Raggio equat. (km) |
|
|
|
|
|
|
|
|
|
|
(6) Raggio medio (km) |
|
|
|
|
|
|
|
|
|
|
(6) Schiacciamento a |
|
|
|
|
|
|
|
|
|
|
Massa (kg) (masse terrestri) |
|
|
|
|
|
|
|
|
|
|
Densità media (kg/dm3) |
|
|
|
|
|
|
|
|
|
|
(7) Gravità all'equatore (Terra = 1) |
|
|
|
|
|
|
|
|
|
|
(8) Velocità fuga (km/s) |
|
|
|
|
|
|
|
|
|
|
(9) Flusso term solare (Terra = 1) |
|
|
|
|
|
|
|
|
|
|
Magnitudine max |
|
|
|
|
|
|
|
|
|
|
(10) Albedo geometrica |
|
|
|
|
|
|
|
|
|
|
(10) Temperatura di corpo nero (K) |
|
|
|
|
|
|
|
|
|
|
Temperatura media (K) |
|
|
|
|
|
|
|
|
|
|
Pressione atmosferica (atm) |
|
|
|
|
|
|
|
|
|
Per l'eccentricità e di un ellisse valgono
le seguenti relazioni: ![]() ed
ed ![]() , con a = semiasse maggiore; b = semiasse minore, c = semidistanza focale (distanza
centro-fuoco) = (Rmax - a) = (a - Rmin), da cui
, con a = semiasse maggiore; b = semiasse minore, c = semidistanza focale (distanza
centro-fuoco) = (Rmax - a) = (a - Rmin), da cui ![]() ,
, ![]() e
e ![]() . Se ne deduce che il semiasse maggiore è pari alla media
aritmetica della distanza massima e minima
. Se ne deduce che il semiasse maggiore è pari alla media
aritmetica della distanza massima e minima ![]() mentre il semiasse
minore è pari alla media geometrica delle suddette distanze
mentre il semiasse
minore è pari alla media geometrica delle suddette distanze ![]()
Il periodo P e la velocità media di rivoluzione V possono essere calcolati in funzione
della distanza media D (pari al
semiasse maggiore a utilizzando la 3a
di Keplero: P2 = k a3 oppure V2 a = k . Esprimendo tutte le variabili in unità terrestri
si ottiene ![]() e
e ![]() La velocità del
pianeta sarà
La velocità del
pianeta sarà ![]() ed il suo periodo
ed il suo periodo ![]()
Il periodo di rivoluzione
sinodico Ps si può calcolare componendo la velocità angolare
rispetto alle stelle fisse della Terra (wT p/PT) e del
Pianeta (wP p/PP). Per i
pianeti interni ![]() . Per i pianeti esterni
. Per i pianeti esterni ![]() Da cui, per i pianeti interni
Da cui, per i pianeti interni ![]() e per i pianeti
esterni
e per i pianeti
esterni![]()
Il moto retrogrado è preceduto dal segno meno e, secondo la convenzione recentemente adottata dall'Unione Astronomica Internazionale (IAU), ai pianeti con moto di rotazione retrogrado si assegna inclinazione dell'asse maggiore di 90 gradi.
L'angolo (in radianti)
sotto il quale il diametro 2R del pianeta viene osservato dalla Terra (da una
distanza D) è pari a 2R/D. Poichè un radiante è pari 360°/2p = 57,29578° = 206264,8
secondi d'arco, il diametro apparente minimo e massimo di un pianeta si calcola ![]() e
e ![]()
Lo schiacciamento polare a di un Pianeta è pari a = (a-b)/a con a raggio equatoriale e b
polare. Da cui il raggio polare è b = a
(1 - a Il raggio medio Rm
è pari ![]() e quindi
e quindi ![]()
La gravità di un Pianeta (in unità terrestri) si calcola facendo il rapporto tra la forza tra la forza di gravità calcolata sul Pianeta e sulla Terra
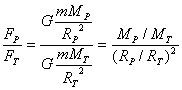
La velocità di fuga può essere calcolata
eguagliando l'energia cinetica all'energia gravitazionale ![]() da cui la velocità di
fuga risulta pari a
da cui la velocità di
fuga risulta pari a ![]()
La quantità di energia solare che colpisce un pianeta per unità di superficie è inversamente proporzionale al quadrato della sua distanza dal sole. Se D è la distanza del pianeta dal Sole (in unità astronomiche), il flusso risulta allora pari a 1/D2 volte il flusso che colpisce la Terra (Costante solare = 1380 W/m2)
Un Pianeta di raggio R
posto a distanza D dal Sole intercetta una frazione di energia solare ![]() pari all'area del suo
disco planetario pR2
fratto l'area totale della superficie sferica 4pD2 investita dal
flusso solare. Se il Pianeta si comporta come uno specchio piano perfettamente
riflettente (albedo A =1) la sua
luminosità totale sarà
pari all'area del suo
disco planetario pR2
fratto l'area totale della superficie sferica 4pD2 investita dal
flusso solare. Se il Pianeta si comporta come uno specchio piano perfettamente
riflettente (albedo A =1) la sua
luminosità totale sarà ![]() . Il flusso luminoso che colpisce la Terra proveniente da una
sorgente estesa (il disco planetario) è direttamente proporzionale al flusso
emesso per unità di superficie
. Il flusso luminoso che colpisce la Terra proveniente da una
sorgente estesa (il disco planetario) è direttamente proporzionale al flusso
emesso per unità di superficie ![]() e all'angolo solido sotto il quale viene vista la superficie
L'angolo solido (in steradianti) è proporzionale al quadrato del diametro
apparente in radianti (2R/DTP)2, dove DTP è la
distanza Terra-Pianeta Il rapporto tra
luminosità intrinseca unitaria Pianeta/Sole è pari a
e all'angolo solido sotto il quale viene vista la superficie
L'angolo solido (in steradianti) è proporzionale al quadrato del diametro
apparente in radianti (2R/DTP)2, dove DTP è la
distanza Terra-Pianeta Il rapporto tra
luminosità intrinseca unitaria Pianeta/Sole è pari a 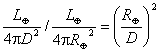 . Il rapporto tra l'angolo solido sotteso Pianeta/Sole è pari
a
. Il rapporto tra l'angolo solido sotteso Pianeta/Sole è pari
a 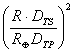 Il rapporto tra il flusso luminoso in arrivo Pianeta/Sole è
allora pari
Il rapporto tra il flusso luminoso in arrivo Pianeta/Sole è
allora pari 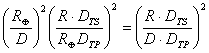 Possiamo confrontare
tale rapporto con il rapporto effettivamente misurato a partire dalla
differenza di magnitudine Sole/Pianeta
Possiamo confrontare
tale rapporto con il rapporto effettivamente misurato a partire dalla
differenza di magnitudine Sole/Pianeta ![]() (con
(con ![]() ). Il rapporto effettivo dei flussi è pari a
). Il rapporto effettivo dei flussi è pari a ![]() . Facendo ora il rapporto tra il valore effettivo e quello
teorico (calcolato nell'ipotesi che A
fosse uguale ad 1) si ottiene una stima dell'albedo del pianeta
. Facendo ora il rapporto tra il valore effettivo e quello
teorico (calcolato nell'ipotesi che A
fosse uguale ad 1) si ottiene una stima dell'albedo del pianeta

|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026