|
|
| |
Imparare le tabelline con le montagne
Questo CD ROM, con le sue filastrocche animate, non vuole presentare soltanto un metodo associativo per insegnare le tabelline, ma vuole approfondirne la comprensione presentando una metafora visiva che, se impiegata correttamente, porterà a un apprendimento cognitivamente superiore del materiale imparato. Alla memorizzazione si potrà affiancare, come attività in classe, l'elemento di ricerca e scoperta delle regolarità e armonie nella tavola pitagorica. Una volta compresa la natura della metafora, sarà più semplice e produttivo esercitarsi anche con la sezione Montagne.
La metafora di cui 545d35f stiamo parlando raffigura ogni tabellina come una catena montuosa, con cime e valli che si alternano continuamente, donando forme caratteristiche a ogni serie di numeri.
Comprendendone la struttura non solo si avrà una migliore comprensione e, dunque, agevolazione nel ricordo ma, allo stesso tempo, sarà possibile facilitare l'apprendimento di tabelline successive partendo da montagne di numeri precedentemente imparate.
L'utilizzo della sezione montagne del CD ROM Tabelline che passione! può profittare della attiva costruzione in classe dei paesaggi che rappresentano ogni tavola pitagorica.
Come si forma la montagna?
Proviamo a prendere come modello la montagna costruita con i numeri della tabellina del due. Tracciamo un diagramma cartesiano in cui indicheremo, sui due assi, i numeri dallo zero al dieci. Nel diagramma riportiamo, in successione, i numeri 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 con l'accortezza di indicare, sull'ordinata, solo i valori unitari di ogni cifra togliendo le decine (ad esempio: la cifra 12 è data da 1 decina e 2 unità. Nelle ordinate del nostro diagramma segneremo, dunque, 2 unità).
Per cominciare, riportiamo i primi cinque numeri della tabellina del 2. Il valore di partenza della tabellina del due è lo zero (2x0) e lo segniamo all'origine del diagramma. Questo punto è l'inizio della montagna.
Il primo salto è di due unità e lo segniamo nell'ascissa di valore 1, costruendo la parte iniziale della montagna.
Arrivati al quinto salto (2 preso cinque volte) si ha un cambiamento: il salto vale 10 unità (1 decina e zero unità). Siccome dobbiamo riportare sull'ordinata soltanto le unità, dovremo scendere dal valore precedente che era otto (2 preso quattro volte) allo zero. Formeremo, così, la prima montagna della tabellina del 2.
Riportiamo ora gli altri cinque numeri della tabellina del 2. Proseguendo con il sesto valore (2 preso sei volte) riprenderemo a salire con la seconda montagna, esattamente come per la prima (avremo, infatti, 1 decina e due unità; riporteremo solo queste ultime sul diagramma).
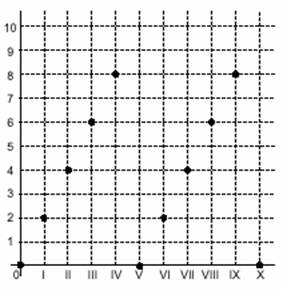
Riportiamo i valori della tabellina del 2 sul diagramma cartesiano.
Unendo i punti riportati si è formata, in questo modo, una "catena di montagne" che raffigura l'andamento regolare interno alla tabellina presa in esame. Arrivati, infatti, al decimo valore (2 preso dieci volte = 2 decine e zero unità) si torna allo zero in ordinata. Andando avanti con l'undicesimo valore la montagna riprenderebbe a salire con la stessa pendenza che ha in precedenza mostrato.
Ogni tabellina manifesta il proprio andamento regolare e armonia con montagne di forma diversa.
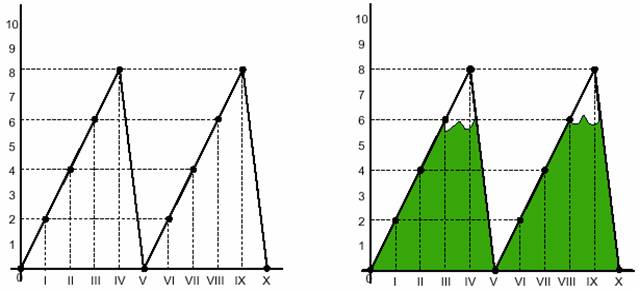
|
Unendo i punti riportati, otteniamo questo grafico. |
Con un po' di fantasia ecco apparire le montagne del 2. |
Potrà sembrare una coincidenza, ma le cime delle montagne costruite con i numeri della tabellina del 2 sono proprio due! Quelle ricavate dalla tabellina del 3 sono tre, quattro quelle della tabellina del 4 e cinque quelle del 5.
Arrivati alla montagna di cinque cime si comincia a tornare indietro. La tabellina del 6 ha quattro cime, tre quella del 7, due quella dell'8 e una sola quella del 9.
Prendendo in esame le coppie di montagne, che hanno numero di cime uguale:
1 e 9, 2 e 8, 3 e 7, 4 e 6;
noteremo una certa similitudine. Con un po' di attenzione, diventerà evidente: le montagne sopra raggruppate sono tra loro speculari.
Per chiarire l'utilità di questa particolare osservazione, torniamo all'esempio della tabellina del 2. La sua montagna ha due cime proprio come la montagna dell'8.
Le due montagne sono esattamente speculari; come dire che la tabellina dell'8 è raffigurata esattamente come quella del 2 ma al contrario!
Se proviamo a leggere la tabellina del 2 partendo dall'ultimo valore, infatti, potremo facilmente ricostruire la tabellina dell'8 (facendo un po' di attenzione alle decine che abbiamo volutamente tralasciare, riportando sul nostro diagramma solo i valori unitari).
Leggendo i valori di ordinata della montagna troveremo: 0, 8, 6 (che con una decina diventa 16), 4 (con due decine diventa 24), 2 (32), 0 (40), 8 (48), 6 (56), 4 (64), 2 (72) e 0 (80). Potremmo andare avanti all'infinito seguendo la regolarità 0, 8, 6, 4, 2.
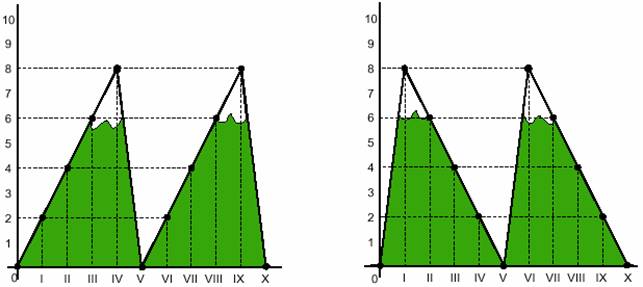
Le montagne dell'8 (a destra) sono esattamente speculari a quelle del 2.
Allo stesso modo potremmo fare con le altre coppie di montagne. L'unica uguale soltanto a sé stessa è quella del 5, la cui regolarità sta nell'alternarsi di 0 e 5.
Le indicazione descritte in questo documento sono state tratte e adattate da:
Craighero G. (1971) Per una didattica psicologica delle operazioni aritmetiche nei problemi della scuola elementare, Giunti.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025