|
|
| |
L'impatto delle geometrie non-euclidee nella storia del pensiero matematico
1. INTRODUZIONE
La maggior parte delle persone probabilmente ignora che, più o meno un secolo e mezzo fa, avvenne nel campo della geometria una rivoluzione che fu profonda, dal punto di vista scientifico, quanto la rivoluzione copernicana in astronomi e importante, dal punto di vista filosofico, quanto la teoria darwiniana dell'evoluzione. In effetti la conseguenza più significativa che ebbe la creazione della geometria non-euclidea fu che essa obbligò i matematici a rivedere radicalmente le loro idee sulla natura della matematica e sui suoi rapporti con il mondo fisico.
Nonostante che i greci avessero riconosciuto che lo spazio matematico astratto è distinto dalle percezioni sensoriali dello spazio reale, tutti i matematici fino al 1800 circa erano convinti che la geometria euclidea fosse l'idealizzazione corretta delle proprietà dello spazio fisico e delle figure al suo interno contenute. Di conseguenza si verificarono molti tentativi per costruire l'aritmetica, l'algebra e l'analisi sulla geometria euclidea, garantendo così anche la verità di queste discipline.
E' altresì degno di nota il fatto che i filosofi della fine del Seicento e del Settecento avessero sollevato il problema di come si potesse essere certi che il corpo di conoscenze più ampio prodotto dalla scienza newtoniana risultasse vero. Quasi tutti, e in particolare Hobbes, Locke e Leibniz, risposero che le leggi matematiche 232i83c , come la geometria euclidea, erano inerenti al disegno dell'universo. L'unica eccezione significativa fu David Hume, che nel "Treatise of Human Nature" (1739) negò l'esistenza di leggi o di successioni necessarie di eventi nell'universo, sostenendo che dall'osservazione di queste successioni gli esseri umani erano indotti a concludere che esse si sarebbero ripetute nello stesso modo. In particolare, le leggi della geometria euclidea non sono verità fisiche necessarie. Questa ipotesi fu controbattuta e soppiantata da Immanuel Kant; egli sosteneva, nella "Critica della ragion pura" (1781), che le nostre menti forniscono certi modi di organizzazione dello spazio e del tempo detti intuizioni e che l'esperienza viene assorbita e organizzata dalle nostre menti in accordo con queste intuizioni. Le nostre menti sono costruite in modo tale da obbligarci a vedere il mondo esterno in un unico modo. Di conseguenza certi principi concernenti lo spazio sono anteriori all'esperienza; questi principi e le loro conseguenze logiche, che Kant chiama giudizi sintetici a priori, sono quelli della geometria euclidea. Sulle basi ora descritte, Kant affermava che il mondo fisico deve essere euclideo e la sua opinione fu quella accettata dal senso comune, che riconosceva l'unicità e la necessarietà della geometria euclidea.
Malgrado la geometria euclidea sia stata considerata per circa 2000 anni la sola e vera scienza adatta a descrivere le proprietà dello spazio che ci circonda, numerosi geometri dall'epoca di Euclide in poi, analizzando criticamente e con rigore la sua opera, si resero conto di alcune imperfezioni e tentarono di rimediarvi; un certo senso di inquietudine rimase comunque, nonostante tutti questi tentativi. Nel 1829 poi comparve la prima vera opera che proponeva esplicitamente la costruzione di una geometria non-euclidea, composta dal matematico russo Lobachevskij, e con essa si può dire che fu segnato l'inizio di una vera e propria rivoluzione in campo geometrico. E' significativo che contemporaneamente a Lobachevskij, idee simili fossero venute a Gauss e a Bolyai, i quali non avevano pubblicato niente sull'argomento: il mondo scientifico era dunque pronto per la rivoluzione.
2. STORIA DEL POSTULATO DELLE PARALLELE
Euclide presentò il V postulato con le parole: " Se una linea retta, incidendo con due linee rette forma angoli interni dalla stessa parte la cui somma è minore di due angoli retti, le due linee rette, se estese indefinitamente, si incontrano dalla parte in cui la somma degli angoli è minore di due angoli retti ".
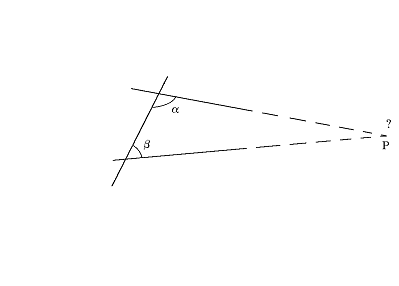
( a b < 180°
Il fatto che Euclide stesso non nutrisse simpatia per questo postulato è evidente: egli rimandò il suo impiego in una dimostrazione il più a lungo possibile, cioè fino alla XXIX proposizione del primo libro degli Elementi. Il postulato fu anche messo in dubbio dai greci del tempo di Euclide e dei secoli successivi.
Proclo (410-485 d.c.) criticò il postulato delle parallele sostenendo che l'affermazione secondo cui le due rette, dato che convergono, si incontreranno in un punto se prolungate, era possibile ma non necessaria. Egli portò a favore della sua ipotesi l'esempio di un ramo di iperbole che si avvicina al suo asintoto senza mai incontrarlo, asserendo che l'opposto della conclusione di Euclide poteva perlomeno essere immaginato. Proclo diceva: " E' quindi chiaro da ciò che dobbiamo cercare una dimostrazione del presente teorema e che esso è alieno dal carattere speciale dei postulati ".
Per oltre 2000 anni alcuni tra i migliori matematici, a partire da Proclo stesso e da Tolomeo, tentarono di dimostrare il V postulato di Euclide. Si giunse così a John Wallis (1616-1703), il più grande matematico inglese prima di Newton. Wallis non cercò di dimostrare il V postulato in geometria assoluta ma propose un nuovo assioma, che riteneva più plausibile di quello delle parallele e dimostrò quest'ultimo a partire dal nuovo assioma e da quelli di geometria assoluta.
Postulato di Wallis: Dato un triangolo qualsiasi ABC e dato un qualsiasi segmento DE, esiste un triangolo DEF, avente DE come uno dei lati, che è simile al triangolo ABC.
Si intende ovviamente che triangoli simili sono triangoli i cui vertici possono essere messi in corrispondenza biunivoca in modo che gli angoli corrispondenti siano congruenti tra loro. Purtroppo il tentativo di Wallis è fallito: non c'è alcuna ragione per considerare il suo postulato più plausibile di quello di Euclide. In realtà si può dimostrare che essi sono logicamente equivalenti (cioè che ciascuno implica l'altro). Si deve ricordare poi il lavoro del gesuita Girolamo Saccheri (1667-1733). Poco prima di morire, pubblicò un libriccino intitolato " Euclides ab amni naevo vindicatus ", del quale non ci si accorse fino ad un secolo e mezzo dopo, quando fu riscoperto dal matematico Eugenio Beltrami. L'idea di Saccheri era di procedere con una dimostrazione per assurdo. Assunse perciò la negazione del postulato delle parallele e cercò di dedurre una contraddizione. Più in dettaglio, egli studiò certi quadrilateri, i cui angoli alla base sono angoli retti e i cui lati verticali sono tra loro congruenti. Questi quadrilateri in seguito sono divenuti noti con il nome di quadrilateri di Saccheri. Si può dimostrare in geometria assoluta (ovvero la geometria euclidea anteriore all'introduzione del V postulato) che in un quadrilatero di Saccheri gli angoli al vertice sono congruenti. Si hanno pertanto i tre possibili casi seguenti:
gli angoli al vertice sono retti.
gli angoli al vertice sono ottusi.
gli angoli al vertice sono acuti.
Volendo dimostrare il primo caso, che è poi il caso della geometria euclidea, Saccheri cercò di vedere che gli altri due conducono a contraddizioni. Riuscì a trovare che il caso 2) porta ad una contraddizione: se gli angoli al vertice fossero ottusi, la somma degli angoli del quadrilatero sarebbe maggiore di 360°, contraddicendo il teorema che afferma che la somma degli angoli interni di un quadrilatero convesso è al più 360°. Benché si occupasse della questione con grande accanimento, non fu in grado di dimostrare che l'ipotesi 3) è contraddittoria. Alla fine affermò deluso che l'ipotesi dell'angolo acuto era assolutamente falsa, semplicemente perché ripugnante per la natura della linea retta. Nonostante non se ne fosse reso conto, Saccheri aveva scoperto la geometria non-euclidea.
In un approccio simile al problema della parallela, Johann Heinrich Lambert (1728-1777) studiò quadrilateri con almeno tre angoli retti, che adesso sono noti con il suo nome. Dedusse inoltre molte proposizioni non-euclidee dall'ipotesi dell'angolo acuto ma, a differenza di Saccheri, non affermò di aver trovato una contraddizione. Lambert dimostrò che l'ipotesi dell'angolo acuto implica che l'area di un triangolo è proporzionale al suo difetto angolare e ricavò che questa ipotesi corrisponde alla geometria su una sfera di raggio immaginario.
3. LA SCOPERTA DELLA GEOMETRIA NON-EUCLIDEA
Come è già stato accennato nell'introduzione, la nascita della geometria non-euclidea non è attribuibile ad un solo matematico: infatti su questa rivoluzionaria teoria lavorarono contemporaneamente, anche se in luoghi diversi e non in contatto fra loro, matematici del calibro di Gauss, Bolyai e Lobachevskij. Fra questi l'unico che pubblicò il suo lavoro fu il russo Lobachevskij, il quale però non fu molto apprezzato finché fu in vita. Il suo lavoro, tradotto in tedesco, fu lodato da Gauss in una lettera inviata al collega russo, nella quale però Gauss ribadì anche la sua priorità in quel campo, come aveva già fatto in occasione dell'analisi del lavoro sullo stesso tema presentatogli da Bolyai. E' opportuno ricordare infatti che Gauss lavorò sulla teoria della geometria non-euclidea fin dall'età di 15 anni. Uno dei motivi per cui non pubblicò mai il suo lavoro, probabilmente il più importante, fu che egli aveva paura degli " strilli dei Beoti ", come scrisse in una lettera a F.W. Bessel nel 1829; Gauss " Nutriva -infatti- una grande antipatia per l'essere coinvolto in qualsiasi sorta di polemica ". Un'altra ragione era il fatto che egli era un perfezionista e il suo grande impegno nei vari rami della matematica e nelle altre discipline scientifiche, in primo luogo astronomia, geodesia e fisica, gli impedirono di portare il suo lavoro in una forma chiara e compiuta come avrebbe desiderato.
Soltanto successivamente alla morte di Gauss, avvenuta nel 1855, quando venne pubblicata la sua corrispondenza, il mondo matematico cominciò a considerare le idee non euclidee seriamente. Alcuni dei migliori matematici del tempo (Beltrami, Klein, Poincarè e Riemann) la estesero, perfezionandola ed applicandola ad altri settori della matematica, tra cui, ad esempio, la teoria delle funzioni complesse. Nel 1868 il matematico italiano Beltrami sistemò una volta per tutte la questione della ricerca di una dimostrazione del postulato delle parallele: mostrò infatti che nessuna dimostrazione era possibile! Ottenne questo risultato dimostrando che la geometria non-euclidea è non contraddittoria nel caso anche la geometria euclidea lo sia, e viceversa.
4. LA GEOMETRIA IPERBOLICA
La geometria iperbolica è, per definizione, la geometria che si ottiene assumendo tutti gli assiomi della geometria assoluta e sostituendo il postulato delle parallele (ad esempio nella forma data da Hilbert: per ogni retta s e per ogni punto P che non giace su s, c'è al più una retta m che passa per P ed è parallela ad s, ovvero che non interseca s.) con la sua negazione, che può essere chiamata "assioma iperbolico".
Assioma iperbolico: in geometria iperbolica esistono una retta s ed un punto P che non giace sulla retta s, tali che almeno due rette parallele a s e distinte passano per P.
Come conseguenza immediata dell'assioma iperbolico si ha:
Lemma: esiste un triangolo la cui somma degli angoli è minore di 180°.
Usando questo lemma, si può ricavare una versione universale dell'assioma iperbolico. Il postulato della parallela in geometria euclidea afferma che per ogni retta e per ogni punto esterno alla retta, vale l'unicità della parallela. La sua negazione, l'assioma iperbolico, afferma che per qualche retta s e qualche punto P esterno ad essa non vale più l'unicità della parallela. Ci si può chiedere se in geometria iperbolica l'unicità della parallela non valga più per qualche retta s e qualche punto P esterno ad essa, ma valga per tutti gli altri punti e le altre rette. Ciò è impossibile, come è affermato dal seguente teorema:
Teorema universale iperbolico: in geometria iperbolica per ogni retta s e per ogni punto P, esterno ad S, passano per P almeno due parallele distinte ad s.
Si hanno subito alcune conseguenze che sono apparentemente sconcertanti per chi è sempre stato abituato a ragionare con mentalità euclidea e a basarsi soprattutto su ciò che può suggerire un disegno, una rappresentazione figurata di ciò che si vuole dimostrare.
Teorema: in geometria iperbolica non esistono rettangoli e tutti i triangoli hanno somma degli angoli minore di 180°.
Questo risultato non è assolutamente campato per aria, non è una pura follia come si poteva inizialmente pensare, ma è solo una conseguenza logica degli assiomi assunti; riguardo a questi non ha senso parlare di verità o falsità e nessuna ragione ci può costringere a respingere l'assioma iperbolico e ad accettare in pieno quello euclideo. In questo caso dobbiamo convincerci che non esistono evidenze, non esistono prove certe, inconfutabili che, ad esempio, la somma degli angoli interni di qualsiasi triangolo sia esattamente 180°. Non si può negare già fin da adesso che quello che è stato creato è veramente un nuovo universo.
Corollario: in geometria iperbolica tutti i quadrilateri convessi hanno somma degli angoli minore di 360°.
Un altro teorema che non ha corrispettivo in geometria euclidea è il seguente:
Teorema: in geometria iperbolica se due triangoli sono simili, allora sono congruenti. (In altri termini, due triangoli sono congruenti se hanno tutti gli angoli congruenti due a due).
Quindi in geometria iperbolica non può valere il postulato di Wallis, poiché quest'ultimo implica il postulato della parallela.
Per riassumere, in geometria iperbolica è impossibile ingrandire o contrarre un triangolo senza distorcerlo.
Una conseguenza notevole del precedente teorema è che in geometria iperbolica un segmento può essere determinato con l'aiuto di un angolo; ad esempio, un angolo di un triangolo equilatero determina univocamente la lunghezza del relativo lato. Sarebbe lecito sostenere che la geometria iperbolica possiede un'unità di lunghezza assoluta.
In geometria euclidea, tracciate due rette parallele, comunque si scelga un punta A su una delle due rette, condotta la perpendicolare all'altra retta, su questa si individua un punto A': la distanza AA' è costante al variare del punto A sulla prima retta e viene detta distanza tra le rette parallele: due rette parallele sono quindi equidistanti.
In geometria iperbolica si dimostra invece il seguente risultato:
Teorema: in geometria iperbolica se s ed s' sono due rette distinte qualsiasi parallele, allora qualunque insieme di punti di s equidistanti da s' contiene al più due punti.
Il teorema afferma che al più due punti alla volta su s possono essere equidistanti da s'. Una figura per rappresentare questo fatto può essere la seguente:
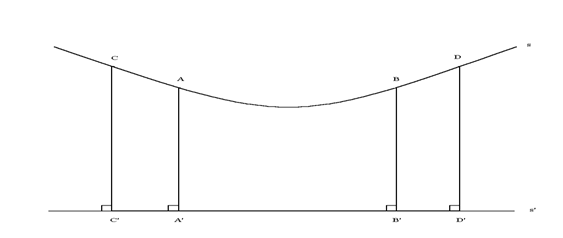
Questa figura suggerisce che il punto "nel mezzo" di s è il più vicino a s' e che s si allontana da s' simmetricamente da entrambi i lati di questo punto medio. Si dimostra che questo è proprio ciò che accade. Tuttavia si deve notare che il teorema precedente non esclude un'altra possibilità, cioè che non ci siano coppie di punti di s equidistanti da s'. Una figura per questo caso potrebbe essere la seguente:
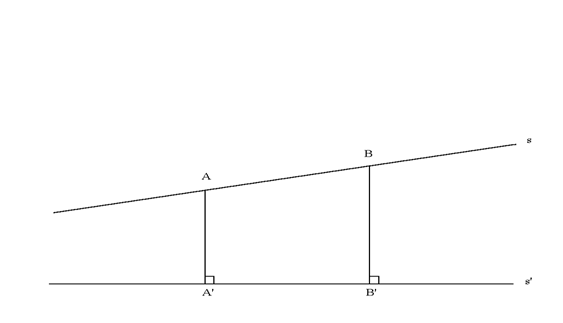 In questa figura i punti su s sono a distanze diverse da
s': s si allontana da s' in una direzione e le si avvicina nell'altra, senza
incontrarla. In tal modo coppie diverse di rette parallele non devono
necessariamente somigliarsi: alcune potrebbero essere come quelle della prima
figura, altre come quelle della seconda.
In questa figura i punti su s sono a distanze diverse da
s': s si allontana da s' in una direzione e le si avvicina nell'altra, senza
incontrarla. In tal modo coppie diverse di rette parallele non devono
necessariamente somigliarsi: alcune potrebbero essere come quelle della prima
figura, altre come quelle della seconda.
E' molto significativo enunciare anche i seguenti teoremi, poiché espongono dei risultati piuttosto chiarificatori su ciò che si può dimostrare a partire dagli assiomi della geometria iperbolica.
Teorema: in geometria iperbolica se s ed s' sono rette parallele per cui esiste una coppia di punti A e B su s equidistanti da s', allora s ed s' hanno un segmento perpendicolare comune che è anche il segmento più corto tra s ed s'. (In questa situazione si verifica ovviamente il caso rappresentato nel primo disegno).
Teorema: in geometria iperbolica, se le rette s ed s' hanno un segmento perpendicolare comune MM', allora sono parallele e MM' è unico; inoltre se A e B sono punti qualsiasi su s tali che M sia il punto medio del segmento AB, allora A e B sono equidistanti da s'.
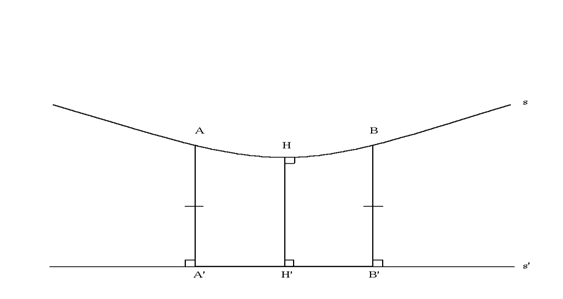
I teoremi precedentemente esposti permettono di raggiungere una buona comprensione del primo tipo di rette parallele. Sappiamo d'altronde che tali rette esistono perché possiamo costruirle. Si considera una retta s qualsiasi ed un punto P esterno ad essa. Dal punto P si traccia la perpendicolare PQ a s e la retta m sia la perpendicolare a PQ nel punto P. Allora m ed s hanno il segmento perpendicolare PQ in comune. Coppie di punti su m disposti simmetricamente rispetto a PQ sono pertanto equidistanti da s. In virtù del teorema iperbolico universale esistono altre rette n passanti per P parallele a s. Tuttavia non siamo in grado di dire che una qualsiasi di tali rette sia una parallela del secondo tipo, poiché n ed s potrebbero avere una perpendicolare comune in un altro punto diverso da P.
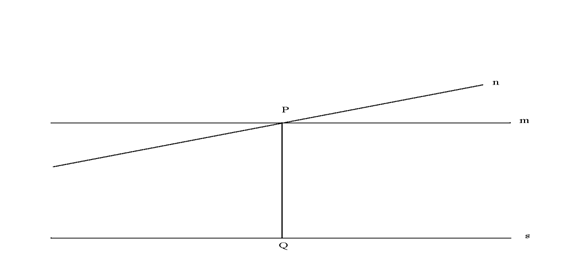
Come possiamo allora accertare che esistono parallele del secondo tipo? Qui entra in gioco l'assioma di continuità. Quella seguente è l'idea intuitiva: consideriamo una semiretta PS della retta m e consideriamo varie rette tra PS e PQ. Alcune di queste semirette, come PR , intersecano s, altre, come PY, no. Un'argomentazione di continuità mostra che quando il punto R si allontana indefinitamente dal punto Q rimanendo su s, PR si avvicina ad una certa semiretta limite PX che non incontra s. La semiretta PX è limite nel seguente senso: qualsiasi semiretta tra PX e PQ interseca s, mentre qualsiasi altra semiretta PY tale che PX è tra PY e PQ, non interseca s. La semiretta PX può essere chiamata semiretta parallela limite sinistra a s per il punto P. Allo stesso modo, c'è una semiretta parallela limite destra dal lato opposto di PQ.
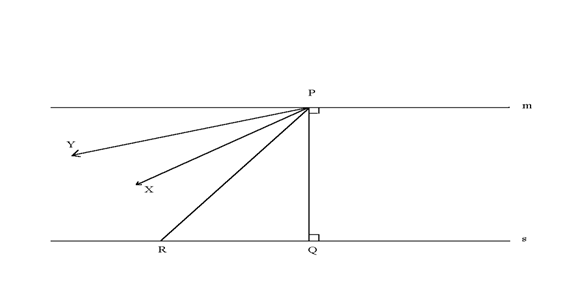
Si può formalizzare questa idea con il seguente teorema:
Teorema: per ogni retta s e per ogni punto P esterno ad s, sia Q il piede della perpendicolare condotta da P a s. Allora ci sono due sole semirette PX e PX', da parti opposte rispetto a PQ, che non incontrano s e hanno la proprietà che una semiretta uscente da P incontra s se e solo se si trova tra PX e PX'. Inoltre queste semirette limite sono disposte simmetricamente rispetto s PQ nel senso che XPQ X'PQ
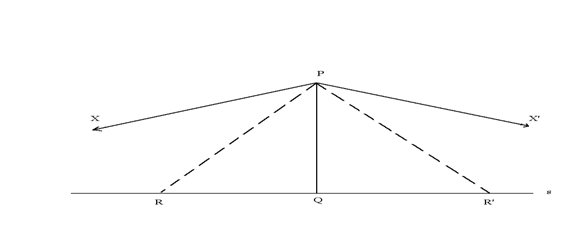
Ognuno dei due angoli congruenti XPQ e X'PQ viene chiamato angolo di parallelismo al punto P rispetto alla retta s. La sua misura in gradi di solito viene indicata con p(PQ)°. si noti che p(PQ)° < 90° poiché, se fosse p(PQ)° = 90°, ciò contraddirrebbe il teorema iperbolico universale. Si può mostrare che, mentre P varia, p(PQ)° assume tutti i possibili valori tra 0° e 90°. Una delle più grandi scoperte di J. Bolyai e di Lobachevskij è la loro formula per questo numero di gradi
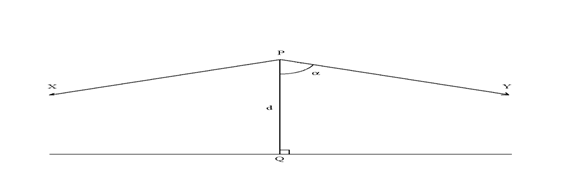 tg a/2 = e -d/k
tg a/2 = e -d/k
dove K è una costante in geometria iperbolica introdotta nel seguente :
Teorema: in geometria iperbolica c'è una costante positiva K tale che, per ogni triangolo ABC si ha:
area (ABC) = (p/180°)K2 * difetto (ABC)
(per cui segue subito come corollario che in geometria iperbolica l'area di ogni triangolo è al più pK2 essendo al più difetto (ABC) = 180°).
In conclusione abbiamo discusso due tipi di rette parallele ad una retta s data. Il primo tipo consiste delle parallele m tali che s ed m hanno una perpendicolare comune, m diverge da s da entrambi i lati della perpendicolare comune. Il secondo tipo consiste delle parallele che si avvicinano ad s asintoticamente in una direzione. Se m è una parallela del secondo tipo, si può dimostrare che s ed m non hanno una perpendicolare comune. Abbiamo così implicato che questi due sono gli unici tipi di rette parallele possibili e questo è il contenuto del seguente teorema:
Teorema: data m, parallela ad s, tale che m non contenga una semiretta limite parallela ad s in nessuna direzione, allora esiste una perpendicolare comune a m ed a s (che è unica per uno dei teoremi precedenti).
Per riassumere, dato un punto P esterno ad una retta s, esistono esattamente due semirette parallele ad s per P, una in ciascuna direzione. Ci sono infinite rette per P che non sono contenute nella regione fra le semirette limite e s. Ognuna di esse è parallela divergente a s e ammette un'unica perpendicolare comune con s (per una di queste rette la perpendicolare comune passerà per P, ma per tutte le altre la perpendicolare comune passerà per altri punti).
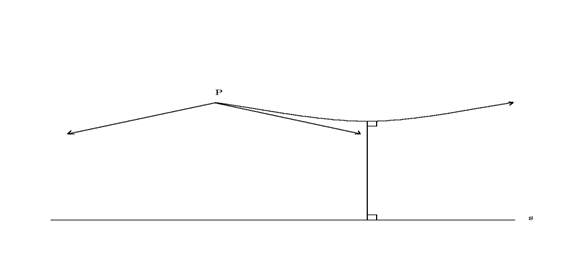 Una parallela alla retta s che contiene una semiretta
parallela limite ad s in una data direzione sarà chiamata una parallela
asintotica in quella direzione, e una parallela a s che ammette una
perpendicolare comune sarà chiamata una retta parallela divergente.
Una parallela alla retta s che contiene una semiretta
parallela limite ad s in una data direzione sarà chiamata una parallela
asintotica in quella direzione, e una parallela a s che ammette una
perpendicolare comune sarà chiamata una retta parallela divergente.
5. INDIPENDENZA DEL POSTULATO DELLE PARALLELE
Dopo aver preso visione dei primi risultati che logicamente si possono ottenere dagli assiomi della geometria iperbolica, si potrebbe pensare che il postulato di base della geometria iperbolica - l'assioma iperbolico - sia falso. Esaminiamo allora cosa potrebbe voler dire affermare che esso è falso. Supponiamo di ammettere che, quando si lascia cadere un oggetto esso cada verso l'alto. Si può eseguire l'esperimento scoprendo che quello che avevamo ammesso è falso. Ora, che tipo di esperimento si potrebbe fare per dimostrare che l'assioma iperbolico è falso, o che la sua negazione, il postulato delle parallele, è vero? Si potrebbe provare a rappresentare una figura. Supponiamo di disegnare la retta PQ perpendicolare a s e la retta m per P perpendicolare a PQ, e quindi una retta n per P, formante un angolo molto piccolo (e gradi) con m. Usando la trigonometria euclidea si può determinare il punto in cui si suppone che n intersechi s, ma se e è abbastanza piccolo, quel punto potrebbe essere a milioni di metri di distanza. Ecco che l'esperimento non sarebbe possibile, vanificando lo sforzo di dimostrare la falsità dell'assioma iperbolico. Ci si può allora domandare se l'assioma conduce ad una contraddizione. Saccheri sosteneva di sì, e per questo cercò di trovare un'argomentazione matematica capace di causare una contraddizione; ma il suo tentativo fallì. Ciò non implica che un giorno qualcuno non trovi una contraddizione. Non c'è infatti nessun teorema che dimostri che la geometria iperbolica è non contraddittoria. Ma lo stesso vale per la geometria euclidea: come sappiamo che essa è non contraddittoria?
E' notevole il fatto che se assumiamo questo implicitamente (assunzione matematica), allora è possibile dare una dimostrazione che la geometria iperbolica è non contraddittoria. Poniamo questa possibilità come un teorema:
I teorema matematico: se la geometria non euclidea è non contraddittoria, allora lo è anche quella iperbolica.
Dando per buono questo risultato, otteniamo il seguente importante corollario:
Corollario: se la geometria euclidea è non contraddittoria, allora non si potrà mai trovare una dimostrazione o una contro-dimostrazione del postulato della parallela a partire dagli altri postulati di Hilbert, ovvero il postulato della parallela è indipendente dagli altri postulati.
Per dimostrare il corollario supponiamo al contrario che esista una dimostrazione del postulato della parallela. Allora la geometria iperbolica sarebbe contraddittoria, poiché l'assioma iperbolico contraddice un risultato provato. Ma il I teorema matematico afferma che la geometria iperbolica è non contraddittoria , relativamente a quella euclidea. Questa contraddizione dimostra che non esiste alcuna dimostrazione del postulato della parallela (dimostrazione per assurdo). Il I teorema matematico, nella formulazione data, è dovuto a Eugenio Beltrami (1835-1900).
Per dimostrare il I teorema matematico dobbiamo ancora chiederci che cosa è una retta in geometria iperbolica; in effetti che cos'è il piano iperbolico? La risposta onesta è che non lo sappiamo, è soltanto un'astrazione. Una retta iperbolica è un termine indefinito che descrive un concetto astratto che assomiglia al concetto di retta euclidea tranne che per le proprietà di parallelismo. Allora, come potremmo visualizzare la geometria iperbolica? La questione della visualizzazione consiste nel trovare oggetti euclidei che rappresentino oggetti iperbolici. Questo significa trovare un modello euclideo per la geometria iperbolica: in questo modo dimostreremo l'indipendenza del postulato della parallela dal sistema di assiomi che forma la base della geometria assoluta.
Il primo modello che consideriamo è detto " modello di Klein ". Fissiamo un cerchio g nel piano euclideo. Se O è il centro di g e OR è un suo raggio, l'interno di g per definizione consiste di tutti i punti X tali che OX < OR.
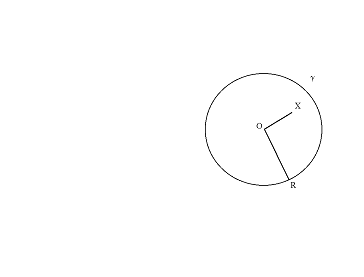 Nel modello di Klein i punti all'interno
di g rappresentano i punti del piano iperbolico. Ricordiamo che
una corda di g è un segmento AB che unisce due punti A e B sulla
circonferenza bordo di g. Consideriamo il segmento senza gli estremi, che
chiameremo una corda aperta )A,B( . Nel modello di Klein le corde aperte di g rappresentano le
rette del piano iperbolico. La relazione " giace su " è rappresentata nel senso
abituale: P giace su )A,B( significa che P giace sulla retta euclidea AB e P
sta fra A e B. La relazione iperbolica " tra " è rappresentata dall'analoga
relazione euclidea. La rappresentazione della congruenza è invece molto più
complicata. E' immediatamente chiaro che l'assioma iperbolico vale in questa
rappresentazione:
Nel modello di Klein i punti all'interno
di g rappresentano i punti del piano iperbolico. Ricordiamo che
una corda di g è un segmento AB che unisce due punti A e B sulla
circonferenza bordo di g. Consideriamo il segmento senza gli estremi, che
chiameremo una corda aperta )A,B( . Nel modello di Klein le corde aperte di g rappresentano le
rette del piano iperbolico. La relazione " giace su " è rappresentata nel senso
abituale: P giace su )A,B( significa che P giace sulla retta euclidea AB e P
sta fra A e B. La relazione iperbolica " tra " è rappresentata dall'analoga
relazione euclidea. La rappresentazione della congruenza è invece molto più
complicata. E' immediatamente chiaro che l'assioma iperbolico vale in questa
rappresentazione:
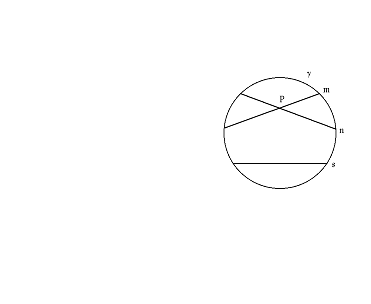
Qui le due corde aperte m ed n per P sono entrambe parallele alla corda aperta s, perché si deve ricordare che la definizione di parallele dice che due rette sono parallele se non hanno alcun punto in comune. Nella rappresentazione di Klein questo diventa: due corde aperte sono parallele se non hanno punti in comune. Il fatto che la tre corde, se prolungate, possono incontrarsi fuori del cerchio g è irrilevante; i punti fuori da esso non rappresentano punti del piano iperbolico.
Riassumiamo allora la dimostrazione di Beltrami-Klein relativa alla non contraddittorietà della geometria iperbolica come segue. In primo luogo si stabilisce un glossario per tradurre i 5 teoremi indefiniti (punto, retta, giace su, tra e congruente) nelle loro interpretazioni nel modello euclideo. In secondo luogo dobbiamo interpretare gli assiomi del sistema. Per esempio il primo assioma dell'incidenza ha la seguente interpretazione nel modello di Klein:
Assioma di incidenza 1 (Klein): dati due punti qualsiasi distinti A, B nell'interno del cerchio g, esiste un'unica corda aperta s di g tale che sia A che B giacciono su s.
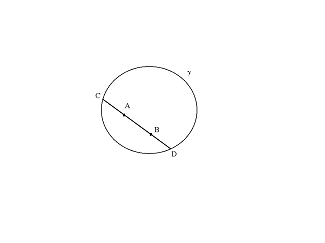
Quando si è dimostrato che tutti i gli assiomi interpretati sono teoremi di geometria euclidea, qualsiasi dimostrazione di una contraddizione entro la geometria iperbolica potrebbe essere tradotta con il nostro glossario in una dimostrazione di una contraddizione in geometria euclidea. Visto che abbiamo assunto che la geometria è non contraddittoria, segue che non esiste alcuna dimostrazione del genere. Così, se la geometria euclidea è non contraddittoria, lo è anche quella iperbolica.
Un aspetto positivo del modello di Klein è che è semplice visualizzare le semirette parallele limite. Sia P un punto interno a g ed esterno alla corda aperta )A,B( . A e B sono punti del bordo di g, quindi non rappresentano punti del piano iperbolico; si dice che rappresentano punti ideali e sono chiamati esterni alla retta iperbolica rappresentata da )A,B( .Allora le semirette parallele limite ad )A,B( da P sono rappresentate dai segmenti PA e PB con gli estremi A, B esclusi. E' chiaro che qualunque semiretta tra queste semirette parallele limite interseca la corda aperta )A,B( , mentre tutte le altre semirette che escono da P non la intersecano.
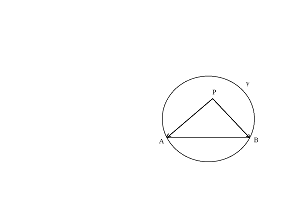
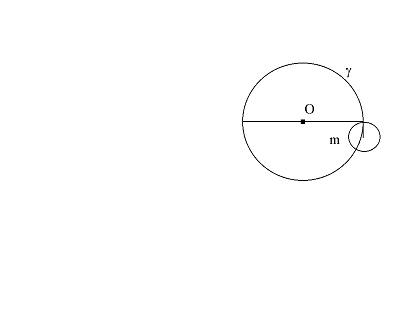
Anche in un modello a forma di disco dovuto ad Henry Poincarè (1854-1912) i punti del piano iperbolico sono rappresentati dai punti interni ad un cerchio euclideo g, ma le rette sono rappresentate in modo diverso. Prima di tutto le corde aperte passanti per il centro O di g (cioè i diametri aperti s di g) sono rette. le altre rette sono date da archi aperti di circonferenze ortogonali al bordo di g. Più precisamente: sia d un cerchio ortogonale a g (in ogni punto di intersezione di g e d i raggi di g e d per quel punto sono perpendicolari). Allora l'intersezione della circonferenza di d con l'interno di g dà un arco aperto m, che, per definizione, è una retta iperbolica nel modello di Poincarè.
Un punto interno a g giace su una retta di Poincarè se giace su essa nel senso euclideo. Ugualmente la relazione " tra " ha l'abituale interpretazione euclidea (se A, B, C sono su un arco aperto di una circonferenza d, ortogonale al bordo del modello, di centro P, B si trova tra A e C se PB è tra PA e PC). L'interpretazione del concetto di congruenza di segmenti nel modello di Poincarè è complicata, essendo basata su un modo di misurare la lunghezza che è diverso dall'abituale modo euclideo, proprio come nel modello di Klein. La congruenza di angoli, comunque, ha lo stesso significato euclideo e questo è il vantaggio più grande del modello di Poincarè rispetto a quello di Klein. Si ricorda che, se due archi circolari orientati si intersecano in un punto A, la misura dell'angolo che formano è il numero dei gradi dell'angolo formato dalle semirette che sono a loro tangenti nel punto A. Se invece un arco circolare orientato interseca in A una semiretta ordinaria, la misura dell'angolo che formano è per definizione il numero dei gradi dell'angolo formato tra la semiretta tangente all'arco in A e la semiretta ordinaria.
 Avendo interpretato
tutti i termini indefiniti della geometria iperbolica nel modello di Poincarè,
otteniamo per sostituzione, le interpretazioni di tutti i termini definiti. Ad
esempio due rette di Poincarè sono parallele se e solo se non hanno punti in
comune. Allora tutti gli assiomi della geometria iperbolica vengono tradotti in
proposizioni di geometria euclidea. Quindi, il modello di Poincarè fornisce
un'altra dimostrazione del fatto che, se la geometria euclidea è non
contraddittoria, lo anche la geometria iperbolica.
Avendo interpretato
tutti i termini indefiniti della geometria iperbolica nel modello di Poincarè,
otteniamo per sostituzione, le interpretazioni di tutti i termini definiti. Ad
esempio due rette di Poincarè sono parallele se e solo se non hanno punti in
comune. Allora tutti gli assiomi della geometria iperbolica vengono tradotti in
proposizioni di geometria euclidea. Quindi, il modello di Poincarè fornisce
un'altra dimostrazione del fatto che, se la geometria euclidea è non
contraddittoria, lo anche la geometria iperbolica.
Le semirette parallele limite nel modello di Poincarè sono illustrate come segue:
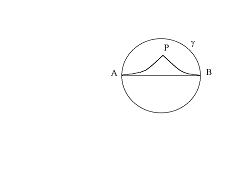
Qui è stata scelta s come un diametro aperto )A,B( ; le semirette sono archi circolari che incontrano AB in A e in B e sono tangenti a tale retta in quei punti. Si può vedere come queste semirette si avvicinino asintoticamente ad s quando ci si muove verso i punti ideali rappresentati da A e B.
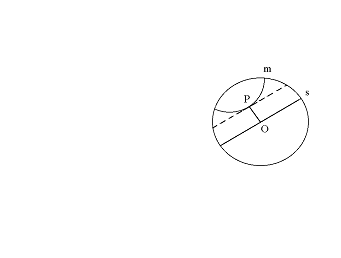
La figura seguente illustra due rette di Poincarè parallele con una perpendicolare comune.
Il diagramma mostra come m diverga da s da entrambe le parti della perpendicolare comune PO.
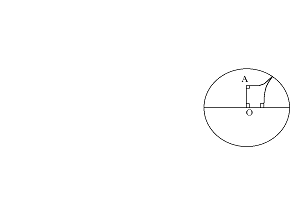
 La
figura seguente invece illustra un quadrilatero di Lambert. Si può vedere bene
che il quarto angolo è acuto:
La
figura seguente invece illustra un quadrilatero di Lambert. Si può vedere bene
che il quarto angolo è acuto:
 Riflettendo la figura rispetto al lato DA otteniamo un diagramma che
illustra un quadrilatero di Saccheri:
Riflettendo la figura rispetto al lato DA otteniamo un diagramma che
illustra un quadrilatero di Saccheri:

Si può essere sorpresi dall'esistenza di due diversi modelli di geometria iperbolica, uno dovuto a Klein e l'altro a Poincarè (c'è addirittura un terzo modello, dovuto anch'esso a Poincarè). Tuttavia si può intuire che questi modelli non sono essenzialmente diversi. In effetti, questi due modelli sono isomorfi, nel senso tecnico che si può stabilire una corrispondenza biunivoca tra i punti e le rette dei modelli in modo da mantenere le relazioni di incidenza, stare tra e congruenza. Si può illustrare questo isomorfismo come segue:
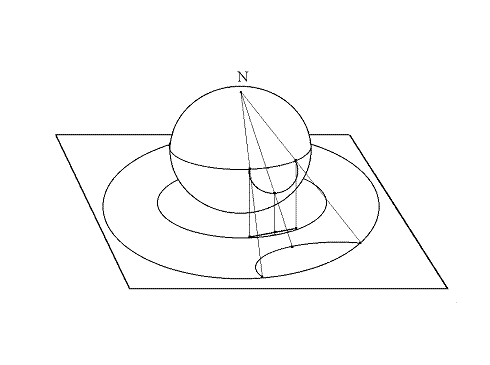
Cominciamo col modello di Klein e consideriamo, nello spazio euclideo tridimensionale, una sfera posta sul piano del modello di Klein e tangente ad esso nell'origine. Proiettiamo ortogonalmente verso l'alto l'intero modello di Klein sull'emisfero inferiore di questa sfera: con questa proiezione le corde del modello di Klein diventano archi di circonferenza ortogonali all'equatore. Proiettiamo allora stereograficamente dal polo nord della sfera sul piano originario. L'equatore della sfera si proietterà su una circonferenza più grande di quella usata per il modello di Klein e l'emisfero inferiore si proietterà stereograficamente nell'interno della circonferenza. Con queste successive trasformazioni, le corde del modello di Klein saranno applicate biunivocamente nei diametri e negli archi ortogonali del modello di Poincarè. In questo modo si può stabilire l'isomorfismo tra i modelli. Veramente si può anche dimostrare che tutti possibili modelli di geometria iperbolica sono isomorfi tra loro. Nell'ulteriore modello di Poincarè prima ricordato, i punti del piano iperbolico sono rappresentati dai punti di uno dei due semipiani euclidei determinati da una retta euclidea fissata. Se usiamo il modello cartesiano del piano euclideo, di solito si sceglie come retta l'asse X e quindi si usa come modello il semipiano superiore che consiste di tutti i punti di coordinate (X,Y) con Y > 0. Le rette iperboliche sono rappresentate in due modi:
come semirette uscenti da punti dell'asse X e perpendicolari all'asse stesso;
come semicirconferenze nel semipiano superiore con centro sull'asse X.
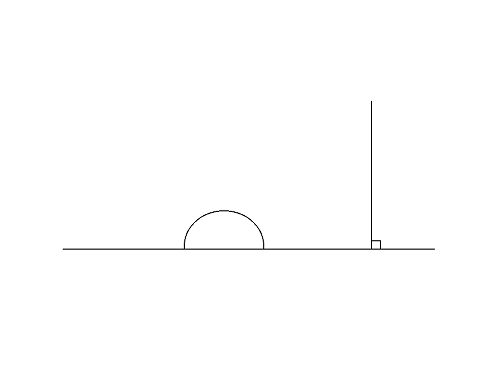
L'incidenza e lo stare tra hanno l'abituale interpretazione euclidea. Per stabilire l'isomorfismo con i modelli precedenti, si sceglie un punto E sull'equatore della sfera della figura precedente e sia p il piano tangente alla sfera nel punto diametralmente opposto ad E. La proiezione stereografica da E su p applica l'equatore in una retta di p e l'emisfero inferiore nel semipiano inferiore determinato da questa retta. Si noti che i punti di questa retta sono punti ideali. Tuttavia manca un punto ideale: il punto E si perde nella proiezione stereografica. Si immagina perciò un punto ideale all'infinito ( ) che corrisponda ad E; esso è l'estremo comune di tutte le semirette verticali.
6. LE DISTANZE IN GEOMETRIA IPERBOLICA
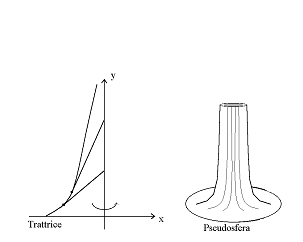
Una difficoltà del modello di Poincarè è che, benché rappresenti fedelmente gli angoli del piano iperbolico, distorce le distanze. Così è naturale chiedersi se esista un altro modello che rappresenti anche le distanze come quello euclideo. Se ci fosse tale modello, sarebbe detto isometrico. Un'idea abbastanza naturale è cercare tale modello in qualche superficie dello spazio euclideo tridimensionale. Le rette del piano iperbolico sarebbero allora rappresentate da geodetiche sulla superficie e ci aspetteremmo che la superficie sia curva, in modo da rispecchiare la nostra sensazione che le rette iperboliche sono realmente curve (per definizione, il segmento di geodetica tra due punti su una superficie è il cammino più corto sulla superficie tra i due punti, come sulla superficie di una sfera un segmento di geodetica è un arco di meridiano). Un difficile teorema di Hilbert afferma che è impossibile applicare l'intero piano iperbolico isometricamente su una superficie dello spazio euclideo. Invece è possibile applicare il piano euclideo isometricamente nello spazio iperbolico, come una superficie detta orosfera. La superficie che rappresenta isometricamente questa regione si chiama pseudosfera. E' ottenuta ruotando una curva, detta trattrice, intorno al suo asintoto. Assomiglia ad un cono infinitamente lungo. In questa rappresentazione i diametri dell'arco di orociclo (curva limite: rappresentata con una circonferenza interna al piano g e tangente internamente ad esso) sono stati identificati - incollati insieme - cosicché l'applicazione del settore nello spazio euclideo è veramente solo un'applicazione della regione tra i diametri. La trattrice è caratterizzata dal fatto che il segmento di tangente da qualsiasi punto sulla curva all'asintoto verticale ha lunghezza costante a. La rappresentazione sulla pseudosfera fu scoperta da Beltrami, usando un lavoro precedente di Minding.
7. CONCLUSIONI
Nei punti precedenti abbiamo dimostrato come la non contraddittorietà della geometria euclidea implichi la non contraddittorietà della geometria iperbolica e viceversa. Viene naturale, dunque, di pensare che entrambe le geometrie debbano essere considerate ugualmente importanti. Per quale motivo, allora, la geometria iperbolica non è utilizzata usualmente per rappresentare il mondo fisico? Molto semplicemente perché la geometria euclidea si adatta perfettamente per la misurazione e l'interpretazione del mondo che ci circonda, come ci è dimostrato dall'ingegneria e dall'architettura. Questo adattamento viene comunque meno nel momento in cui si passa alla misurazione di distanze maggiori rispetto a quelle usuali. Potremmo, infatti, pensare che la somma degli angoli interni di un triangolo, i cui vertici sono molto distanti (per esempio tre stelle), non sia esattamente 180°. Gauss provò ad effettuare questo esperimento, misurando la somma degli angoli interni del triangolo i cui vertici erano le cime di tre montagne. La sua misurazione risultò essere di molto inferiore a 180°, ma il suo esperimento non si può ritenere valido a causa dell'errore degli strumenti utilizzati nella misurazione. Può esserci comunque utile come spunto di riflessione. Proviamo allora ad immaginare che il risultato della misurazione fosse stato esattamente di 180°, con un errore di di grado. Possiamo solo concludere che la somma poteva variare fra 179.99° e 180.01°. Immaginiamo adesso che la misurazione fosse risultata di 179°, con il medesimo errore: ciò vuol dire che la somma può variare tra 178.99° e 179.01°. In questo caso saremmo stati certi che il risultato è inferiore a 180°: l'esperimento avrebbe così dimostrato che lo spazio fisico è iperbolico. Riassumendo, se fossimo in grado di compiere delle misurazioni precise, si potrebbe dimostrare soltanto che lo spazio fisico è iperbolico.
Potremmo allora concludere che entrambe le geometrie possono essere parimenti sfruttate: quella euclidea per quanto riguarda lo spazio fisico, quella iperbolica per quanto riguarda lo spazio astronomico. Purtroppo fare un discorso come questo è troppo semplicistico.
E' opportuno, infatti, indagare la natura dei nostri strumenti: essi sono progettati sulla base di ammissioni euclidee; indagare la nostra concezione di rette: non potrebbe darsi che i raggi luminosi viaggino su traiettorie curve? Dobbiamo indagare se lo spazio, specialmente l spazio di dimensioni cosmiche, non può venire descritto da geometrie diverse dalle due suddette. Quest'ultimo problema, in effetti, è coerente con l'odierno atteggiamento scientifico. Secondo Einstein, lo spazio e il tempo sono inseparabili e la geometria dello spazio-tempo è tale che i raggi luminosi sono veramente incurvati dall'attrazione gravitazionale esercitata dalle masse. Lo spazio non è più concepito come una vuota scatola Newtoniana, i cui contorni sono alterati dalle masse poste al suo interno. Il problema è molto più complicato di quanto mai immaginarono Euclide o Lobachevskij: nessuna delle loro geometrie è adeguata per l'attuale concezione dello spazio. Questo non diminuisce l'importanza storica della geometria non euclidea. Einstein disse: "A questa interpretazione della geometria io attribuisco grande importanza, perché, se non l'avessi avuta presente, non sarei mai stato in grado di sviluppare la teoria della relatività".(Infatti Einstein sviluppò una geometria appropriata alla relatività generale dalle idee di Riemann).
Si riporta ora la famosa risposta di Poincarè alla domanda su quale sia la geometria vera:
"Se la geometria fosse scienza sperimentale, non sarebbe una scienza esatta. Sarebbe soggetta a revisioni continue..... Quindi gli assiomi geometrici non sono intuizioni sintetiche a priori, né fatti sperimentali. Sono convenzioni. La nostra scelta tra tutte le possibili convenzioni è guidata dai fatti sperimentali; ma rimane libera ed è soltanto limitata dalla necessità di evitare ogni contraddizione, ed è così che i postulati possono rimanere rigorosamente veri anche quando le leggi sperimentali che hanno determinato la loro scelta sono solo approssimate. In altre parole gli assiomi della geometria (non parlo di quelli dell'aritmetica) sono solo definizioni camuffate. Allora, che cosa dobbiamo pensare della questione: la geometria euclidea è vera? Ciò è privo di senso. Ugualmente potremmo chiederci se il sistema metrico è vero e se i vecchi pesi e misure sono falsi, se le coordinate cartesiane sono vere e quelle polari false. Una geometria non può essere più vera di un'altra: può solo essere più conveniente. ". Si potrebbe pensare che la geometria euclidea sia la più conveniente: lo è per l'ordinaria ingegneria, ma non per la teoria della relatività. Per di più, c'è chi sostiene, ad esempio Luneberg, che lo spazio visivo, lo spazio tracciato nel nostro cervello attraverso i nostri occhi, sia descritto in modo più appropriato dalla geometria iperbolica.
Questa discussione getta nuova luce su ciò di cui si occupa la geometria e, in generale, la matematica. La geometria non tratta i raggi luminosi, ma la traiettoria di un raggio luminoso è una possibile interpretazione fisica del termine geometrico, indefinito "retta". Bertrand Russel disse una volta: "La matematica è la scienza in cui non si a di che cosa si stia parlando ne se quello che si dice sia vero". Questo perché certi termini primitivi, come punto, retta e piano sono indefiniti e potrebbero essere sostituiti da altri termini senza mutare la validità del risultato. Invece di dire: "due punti individuano un'unica retta", si potrebbe dire: "due alfa determinano un unico beta". Nonostante questo cambio di termini, le dimostrazioni di tutti i teoremi sarebbero ancora valide, poiché le dimostrazioni corrette non dipendono dai diagrammi: dipendono solo dagli assiomi posti e dalle leggi della logica. Così, la geometria è puramente un esercizio formale nel dedurre certe conclusioni da certe premesse formali. La matematica fa affermazioni del tipo "se....allora...."; non dice niente sul significato o sulla verità delle ipotesi. Le nozioni primitive (come punto e retta) che compaiono nelle ipotesi sono definite implicitamente da questi assiomi, dalle regole che, così per dire, ci dicono come giocare. Il punto di vista formalistico fin qui presentato è radicalmente opposto alla più vecchia idea secondo cui la matematica afferma "verità assolute", un'idea che venne distrutta definitivamente dalla scoperta delle geometria non-euclidea. Quest'ultima ha avuto un effetto liberatorio sui matematici, che adesso si sentono liberi di creare qualsiasi insieme di assiomi a loro piaccia, e di dedurre le più diverse conclusioni. In effetti questa libertà potrebbe giustificare il grande aumento in estensione e generalizzazione della matematica moderna.
In un discorso del 1961 Jean Diendonnè osservò a proposito della scoperta di Gauss della geometria non-euclidea:
"Fu una svolta di capitale importanza nella storia della matematica, poiché segnò il primo passo verso una nuova concezione della relazione tra il mondo reale e i concetti matematici ritenuti in grado di spiegarlo; con la scoperta di Gauss, il punto di vista piuttosto ingenuo che l'oggetto della matematica fossero soltanto "idee" (nel senso platonico) di cose sensibili divenne insostenibile, e gradualmente fece strada ad una migliore comprensione della molto più grande complessità della questione, riguardo alla quale oggi ci sembra che la matematica e la realtà siano quasi completamente indipendenti e che i loro punti di contatto siano più misteriosi che mai". Questo pensiero sembra riportarci al filosofo greco Eraclito, secondo il quale la realtà non è conoscibile per gli uomini, ma è un ente misterioso, che addirittura si nasconde alle loro affannose ricerche.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025