Uso derivate:Interpolazione dati: fitting minimi quadrati

Equazioni lineari(1°2°) e non, equazioni differenziali (esempi)

Integrazione:definizione come limite e inverso derivazione,regole,uso

Soluzione eq differenziali lineari omogenee e non, variabili separabili

Appendici (nr complessi, sol equazioni diff 2 ordine

Sviluppo di Fourier per funzioni periodiche, risposta in frequenza

INTRODUZIONE

Il linguaggio nasce dalla necessità di trovare un codice simbolico comune (oggettivo), per trasmettere informazioni tra sistemi diversi .

Il linguaggio organizzato si serve di un numero limitato di simboli (base simbolica ).

Un numero limitato di regole di collegamento tra i simboli permette di creare un numero praticamente illimitato di simboli complessi.

1-Linguaggio parlato(comunicazione on-line)

a- lettere (a,b,c.): alfabeto

b- parole : vocabolario.Associazione con ripetizione delle lettere (parole). Regole di

associazione variabili : diverse lingue

c- frasi: generate da operazioni tra vocaboli : affermazione è, negazione non , meno, più, o

(OR somma logica), e (prodotto logico AND)

Operazioni più complesse sono derivate dalle precedenti

Es: o interrogativo aaa o bbb ? = (non aaa AND bbb ) or ( aaa AND non bbb )

d- discorso: Collegamento tra frasi con regole associative

2-Linguaggio scritto (comunicazione differita)

Rappresenta con modifiche convenzionali di un supporto fisico , le lettere (caratteri), le parole, le frasi ed i discorsi

3-Linguaggio matematico (aggiunta quantitativa al linguaggio parlato

a- cifre alfabeto numerico

b- numero : associazione con ripetizione. Regole di associazione variabili. Particolarmente importante la struttura detta a base

- scelta di N cifre (base N) a1,a2,..aN

- costruzione ordinata del numero da sinistra a destra, come somma di cifre per potenze*

successive della base. Indicando con un indice una delle cifre, il numero è costruito:

Ordine della potenza: ... 4 3 2 1 0

Cifra ... ai aj ak am an

Si legge: ai.N⁴ + aj.N³ + ak.N² + am.N¹ + an.N⁰

es: 123 in base 10:

123 in base 6: 123₆ = 1.(6.6) + 2. (6 ) +3 .(1) = 51₁₀

c - Espressioni numeriche(frasi). Generate da operazioni tra numeri

somma (+) Estensioni:

prodotto (a n) :somma ripetuta n volte dello stesso numero a

potenza: ( aⁿ) :prodotto ripetuto n volte (esponente) del numero a (base)

sommatoria S _i ^1,n a _i somma ripetuta n volte di grandezze a _i simili

somma integrale limite di S _i ^1,n per n che tende a infinito ed a _i a zero

opposto(-) (Presuppone lo ZERO):definisce negativo l' opposto di un numero

Estensione : la sottrazione (-) come somma di un numero e

dell'opposto di un altro a-b = a + (-b)

inverso(I): numero che moltiplicato ad uno dato dà come risultato uno: a I(a) = 1

Estensioni: divisione( / ): a / b = a I(b)

d)Descrittori geometrici ;

Angolo (inclinazione tra due direzioni) : rapporto arco/raggio: a/R ) a

R R

proiezioni (ombre) : seno= s /R s

coseno = c/ R c

Cerchi, sfere ( raggio R)ecc

- Perimetro della circonferenza 2pR  p

- Area del cerchio   p R²

- Area della sfera 4p R²

- Volume della sfera 4/3 p R³

- Angolo solido = s/ R²

e)Metodi proiettivi in medicina

a)occhio (pin hole)

b)Radiografia (trasmissione),Scintigrafia (emissione)

c)Tomografia (trasversale e longitudinale nei casi precedenti)

a)

b)

c)

B-Richiami su regole operazionali di ordine "superiore"

Può essere utile un richiamo sulle regole operazionali delle potenze e dei logaritmi, anche per gli studenti più esperti del calcolo.

1-Potenze

-Esponente 0 x⁰ = 1 qualunque sia x

- Esponente negativo    x ^-a = 1 / x^a

-Prodotto di potenze con stessa base x^a x^b = x^a+b

Potenza di potenza ( x^a ) ^b= x ^{a b}

Prefissi (sigle preposte ad un numero o ad una grandezza (multiplo o il sottomultiplo)

Nome potenza dieci simbolo

Tera 10¹² T

Giga 10⁹ G

Mega 10⁶ M

Kilo 10³ K

hetto 10² h

deci 10^-1 d

centi 10^-2 c

milli 10^-3 m

micro 10^-6 m

nano 10^-9 n

pico 10^-12 p

2- Logaritmi

E' l'operazione inversa alla potenza:

Dato un numero a, si 252c22c deve trovare la potenza p e cui va elevato un valore di riferimento b (base) per ottenere il numero in esame

p

b = a

p è il logaritmo di a in base b ( basi usate sono : 10 ; e (2.718..) ; e 2 in informatica)

Si scrive formalmente

log _b a

p = log _b a equivale a >> b = a

equivale a

NB: Qualunque sia la base b ln _b 1 = 0

log _b b =1 (esponente da dare a b per avere b)

Regole operative

- logaritmo di un prodotto ln _b (x y) = ln _b x + ln _b y

- logaritmo di un rapporto ln _b (x/y) = ln _b x - ln _b y

- logaritmo di una potenza ln _b (x^a ) = a . ln _b x

La regola di potenza

spiega il segno negativo per logaritmi di numeri tra 0 ed 1 .

es: 0.000x = x 10^-4 = -4+log x

Permette di trasformare (linearizzare) una equazione:

Es: y = a^bx+1 applicando l'operatore log > log y = bx+1

- Cambio di base ln _b x = ln _a x ln _b a es ln _ex = ln ₁₀ x ln _e 10

la regola precedente comporta in particolare che se a=1/b

ln _b x = ln _1/b x ln _b 1/b = ln _1/b x (-ln _b b) =

ln _b x = - ln _1/b x

3-richiamo su equazioni:

Relazione operazionale tra numeri noti salvo un'incognita ,il cui risultato è zero

(a,b,c,+,-,exp,log.,xⁿ) = 0

n= ordine dell'equazione: valore dell'esponente massimo in cui l'incognita compare. L'ordine pilota il numero di valori numerici attribuibili all'incognita per soddisfare l'eguaglianza a zero dell'equazione)

(a,b,c,+,-,exp,log.,xⁿ) = 0

Se esistono due valori di x coppie x1 x2 che soddisfano l'equazione, se anche la somma x1+x2 soddisfa l'equazione questa è detta lineare

INSIEMI DI VALORI E LORO RELAZIONI (FUNZIONI)

1-Descrizione di insiemi di valori numerici dello stesso "oggetto"

Campione- istogramma di frequenza ( come sono distribuiti) - media ,moda,mediana (eventuali sottoinsiemi)- descrittori numerici d'insieme (momenti)-estrapolazione a campione infinito ("limite" dei descrittori aumentando il campione ). (vedi Statistica)

2- Descrizione delle relazioni tra insiemi

Funzione di una variabile :Se due grandezze X e Y possono assumere rispettivamente due insiemi di valori x_i, y_i . Se ad ogni valore x in X corrisponde almeno un valore un valore y in Y, si dice che Y è funzione di X.

Espressione formale: Y = f (X)

Può verificarsi che:

a- ad x corrisponde un solo valore y

b- ad x corrispondono più valori di y (cerchio,spirale ecc)

c- Si può invertire, ossia esiste una funzione inversa :

Se per y= f(x) esiste x= f^-1 (y) per cui y= f(f^-1 (y)) ossia f f^-1= 1

es: y= 2 x > x = y/2

d- Si chiama campo di esistenza l'insieme di valori di x per cui esiste la relazione

Rappresentazione grafica

Per interpretare, riassumere e riconoscere un fenomeno espresso dalla relazione tra due variabili y=f(x), la rappresentazione grafica è di estrema utilità. Il modo più usato di rappresentazione consiste nel scegliere due direzioni orientate perpendicolari :assi coordinati cartesiani ortogonali.(fig a) Ai valori numerici delle due variabili viene fatto corrispondere un segmento sugli assi corrispondenti, scelto un opportuno segmento per i relativi valori unitari.

Molto spesso, viene anche utilizzato un diverso modo di rappresentazione:la rappresentazione polare . In questo caso, la realzione y=f(x), viene trasformata nella relazione r=f(a) dove

r= (x² + y²) e a = arctg (y/x).(fig b) Quest'ultima relazione è di particolare interesse in medicina , dove molte grandezze fisiologiche caratteristiche hanno andamento ciclico nella giornata. (Fig c)In tal caso l'angolo viene fatto corrispondere all'ora o del giorno

a = o . 2p/24. Questo ultimo tipo di rappresentazione è utilizzata spesso per rappresentare un qualunque tipo di fenomeno periodico a periodo T,tale cioè che

y(x) = y(x+T)

Fig: rappresentazioni grafiche: a)cartesiane ortogonali ; b) polari ; c) orarie

Funzioni base,parametri

La necessità di esprimere il legame tra grandezze fisiche, implica nelle relazioni di eguaglianza, sia l'eguaglianza del valore numerico, che del tipo o dimensione delle grandezze. Nelle relazioni operazionali tra variabili fisiche, compaiono allora un dato numero di grandezze numeriche a1,a2..an , parametri che giustificano l'eguaglianza dimensionale. Tali grandezze inoltre che modulano il risultato numerico dell'operazione, ma non la tipologia operativa in fenomeni noti relativi a sistemi fisici dello stesso tipo.

La relazione tra due variabili y,x, è allora descritta in forma generale come

y = f( x,a1,a2..aN)

Le più frequenti relazioni fisiche, sono

Linearità : y= a1.x+a2

Potenza : y = a1.x^a2

Esponenziale y= a1. e ^x.a2 ( e=2.718.)

Logaritmo y = a1 log _a2 (x) (più frequentemente nella forma B=e=2.718 o B=10)

Sinusoide y= a1. sen( a2.x +C) a1: ampiezza; a2 = pulsazione= 2pF

F =frequenza: T= 1/F periodo

In tutti i campi dell'analisi dati riguardanti un fenomeno fisico in cui è nota la modalità operativa tra variabili, la differenza di comportamento del sistema in cui si osserva il fenomeno è data dai valori dei parametri stessi.

Ad es

Se in un insieme di sistemi fisici dello stesso tipo, si sa a priori che la dipendenza di

Una grandezza y dalla grandezza x è espressa dalla relazione y = a.x +b .

Il singolo sistema è individuato allora dalla coppia di parametri a,b .

Per descrivere l'insieme di tutti i sistemi, si utilizza allora un diverso spazio nel quale

ogni sistema è individuato dal punto di coordinate (a,b).

La metodica con cui per descrivere un fenomeno viene utilizzato uno spazio i cui i punti sono individuati dalle coordinate parametriche, viene individuata col termine di "trasformata di spazio"

Funzione di più variabili

Molto spesso, nell'ambito della studio di un sistema fisico, una delle grandezze coinvolte (Y) dipende da N diverse altre grandezze ,indipendenti tra loro, ciascuna delle quali può assumere un valore variabile (x_i ) in un dato insieme (X). In questo caso la variabilità di Y dipende da N variabilità. Si dice che Y è funzione di N variabili, scrivendo:

Y = f( X1,X2..XN) *)

Per valutare la modalità della dipendenza di Y dalle altre grandezze, si scompone la *) in N diverse relazioni operazionali, in ciascuna delle quali le operazioni considerate sono solo quelle sulla variabile "corrente".Le altre variabili,in tale relazioni, sono viste come valori costanti . Per es:

Y = sen( 2.x)/ (z² + log (w)) > f(x,z,w)

Si valuta come:

Y = sen (2x) / costante > f1(x)

Y = costante / (z² + costante) > f2(z)

Y = costante/ (costante + log(w)) > f3(w)

e si procede come nel caso a- per le singole relazioni,(limiti,continuità ecc)

c4- Funzione di funzione

Può avvenire che una grandezza Y dipenda da una grandezza Z , e Z dipenda da una grandezza W

Y = f( Z ) ; Z = f1( W ) **)

In questo caso Y è : funzione di funzione di W in quanto dipende , in modo indiretto, da W

Y = f( f1(W))

La dipendenza operativa di Y da w,si studia, con i metodi visti in a-, utilizzando le **)

Vettori

Una grandezza fisica G definita da un unico valore numerico (multiplo di una opportune unità di misura) è detta scalare .

Una grandezza fisica G per la cui definizione necessitano due o più valori numerici (multipli di una opportuna unità di misura ) è detta vettore.

Il numero n di valori che definiscono un vettore è detto ordine del vettore stesso e la grandezza è indicata con

G _n (g ₁ ,g ₁ ,..g _n )

Dove i valori g ₁ ,g ₁ ,..g _n sono le componenti del vettore

Un grandezza fisica G definita da m vettori di ordine n ,ossia da m.n valori numerici è detta matrice di ordine m.n ( m righe ed n colonne)

g _1,1 ,g _1,2 ,..g _1,n

G _m,n g _2,1 ,g _2,2 ,.. g _2,n

..........................

g _m,1 ,g _m,2 ,.g _m1,n

Il concetto di entità definita da più simboli può essere esteso fino all'infinito.

Consideriamo per esempio una immagine digitale che descrive la distribuzione piana di una data grandezza fisica su una superficie S, tramite m.n valori numerici di questa ,ciascuno dei quali rappresenta il valore medio misurato per quella grandezza in un elemento s di superficie (pixel) con

s= S/m.n.

Una sucessione di k immagini è a sua volta descritta da un insieme di m.n.k elementi ,ossia da un'entità numerica G _k,m,n

Le operazioni lecite su entità descritte da più numeri ,debbono essere coerenti con le operazioni possibili su un solo numero. Infatti uno scalare puo' essere indicato come G _1,1,1 .

Proprietà e regole operazionali di un insieme vettoriale

-Vettore nullo:dato un insieme vettoriale di ordine n, G _n (g ₁ ,g ₁ ,..g _n ), si definisce nullo il vettore le cui componenti sono tutte nulle G _n

-Vettore somma: dati due vettori dello stesso ordine G_n (g ₁ ,g ₁ ,..g _n ) , v_n (v₁,v ₂ ,.v _n )

il vettore somma S _n = G_n + v_n è:

S _n (g ₁+ v₁, g ₂+ v₂ ,..g _n + v_n)

-Vettore opposto :Il vettore opposto ad un vettore G _n (g ₁ ,g ₁ ,..g _n ) è quello che sommato a G_n dà il vettore nullo.Le componenti di tale vettore sono eguali ed opposte alle componenti del vettore G _n

-Vettori uguali : due vettori sono eguali allora e solo se le loro componenti sono eguali.

-Prodotto di un vettore per uno scalare: se un vettore viene moltiplicato per un numero ,si ottiene un vettore le cui componenti sono quelle del vettore iniziale moltiplicate per quel numero

a.G _n (a.g ₁ ,a.g ₂ ,.. a.g _n )

-Prodotto tra due vettori : Il prodotto (x) tra due vettori è uno scalare dato dalla la somma dei prodotti delle componenti omologhe. Se i due vettori sono

G_n (g ₁ ,g ₁ ,..g _n ) ; v_n (v₁,v ₂ ,.v _n )

il loro prodotto è:

_i=1,n

G_n x v_n = _i g_i v _i

-Vettori ortogonali : due vettori sono detti ortogonali se il loro prodotto scalare è nullo. Se due vettori sono ortogonali ,una loro qualsiasi combinazione lineare da un vettore non nullo

- Modulo di un vettore: la moltiplicazione di un vettore per se stesso da uno scalare,la cui radice quadrata ( ,è detta modulo del vettore

_i=1,n

v = (v _n x v _n ) = _i (v_i v _i )

-Versore di un vettore: Moltiplicando un vettore per uno scalare dato dall'inverso del suo modulo si ottiene un vettore u _v in cui la relazione tra le componenti resta immutato ma che ha modulo unitario . Tale vettore è detto versore del vettore.

v 1/v = u _v

Dalla precedente otteniamo una espressione esplicita del vettore come : prodotto di uno scalare (modulo) per un versore unitario

v = v u _v

-Vettori indipendenti (linearmente): un gruppo di k vettori sono detti linearmente indipendenti se una qualsiasi loro combinazione lineare (somma dei vettori moltiplicati per k costanti arbitrarie) è sempre diversa dal vettore nullo salvo il caso che le k costanti moltiplicative siano tutte nulle.

Il risultato di tale combinazione è allora un vettore non nullo dello stesso ordine.

_i a _i .G _i = v

Base vettoriale : Dato un insieme vettoriale di ordine n, è possibile selezionare nell'insieme n vettori linearmente indipendenti: una base vettoriale .Se i vettori della base sono ortogonali tra loro la base è detta "ortogonale". Se gli n vettori ortogonali hanno modulo unitario la base è detta "ortonormale"

Utilizzando una base ortonormale i1,i2..ik , un qualsiasi vettore di ordine k può scrivere

_j=1..k

V = v1 i1 + v2 i2 +...vk ik = S_j vj ij

dove uno dei coefficienti della combinazione vn (n=1.k) è ricavato come

_j=1..k

vn = V x in = ( S_j vj ij ) x in

Rappresentazione grafica di vettori ,espressione geometrica.

I vettori comunemente incontrati nell'osservazione fisica spaziale di un sistema, fanno riferimento alle da tre componenti x1,x2,x3 ( coordinate ) di un punto P in un sistema prefissato di riferimento spaziale ed alle loro variazioni (d )nel tempo e nello spazio (velocità ,accelerazione forze campi ecc.)

Tali vettori sono espressi come combinazione lineare di tre vettori unitari perpendicolari (i versori delle direzioni di riferimento o "assi"), che rappresentano la base vettoriale ortonormale dell'insieme.

Ad esempio il vettore posizione PO in un sistema cartesiano ortogonale avente origine in O si ottiene da una combinazione lineare dei tre versori di base unitari perpendicolari i,j,k :

PO = xi + yj + zk a)

Vettori ottenuti da PO per differenza e/o moltiplicazione di un valore costante, quali velocità, forza ecc., hanno quindi espressioni analoghe alla a) o alla b)

V = Vx i + Vy j + Vz k ; V = V.uv

In tale rappresentazione grafica, la singola componente Vx di un vettore V , rappresenta la proiezione di V sull'asse x . Se a è l'angolo formato dal versore uv del vettore con il versore i dell'asse x, sarà:

Vx = V. cos a

Si dimostra che il prodotto scalare tra due vettori V1 e V2, dove j è l'angolo compreso tra i relativi versori è dato da

V1 x V2 = V1.V2. cos j

Tra due vettori V1, V2, esiste un ulteriore tipo di prodotto :il prodotto vettoriale che genera un vettore Vt

V1 ^ V2 = Vt

Nella rappresentazione grafica sopradetta, se j è l'angolo compreso tra i relativi versori, il modulo di tale vettore è dato da

Vt= V1.V2.sen j

Il versore di Vt è ortogonale ad entrambi i vettori ed orientato con la regola della mano destra(V1 pollice, V2 indice, Vt medio)

Basi particolari

Se abbiamo un insieme di N vettori di ordine n, la scelta della base può essere decisa dall'operatore. La scelta si orienta ,salvo casi particolari, verso una base ortonormale.

La scelta del tipo di base può essere sostanzialmente di 2 tipi: una base caratteristica dell'insieme, o una base generale, che si presta per tutti gli insiemi vettoriali dello stesso ordine.

Base di Fourier

La più usata è una base del secondo tipo, i cui vettori sono dati da sequenze sinusoidali

dove i termini hanno periodi sottomultipli di n. Se indichiamo con w la pulsazione fondamentale

w = 2p/n

la più usata è formata dalle sequenze di n/2 seni ed n/2 cos (con i=1,n)

1/ n sen (k w i), 1/ n cos (k w i) con k=0,n/2

Tale base è detta base di Fourier

NB: se n è dispari è poco importante in quanto sen (n p/2.n i)= sen (p.i)=0 e quindi i vettori della base restano in totale in numero n

Base di Hotelling

Questa base è ricavata con metodi statistici, dall'insieme in esame. E molto usata se i vettori rappresentano misure di una grandezza nelle sue n variazioni temporali o spaziali, in quanto permette di minimizzare l'errore di misura, rappresentando ogni vettore con un gruppo di m<< n vettori (componenti principali) . Esprimendo ciascun vettore con tale base, si ottiene un "filtraggio (minimizzazione)" dell'errore di misura.

Tale base è molto usata in psicologia , ma anche nella descrizione di immagini mediche.

Limite fisico e matematico

In diversi fenomeni fisici, la relazione tra due grandezze y,x può non essere definita per un valore xo della variabile indipendente x. Spesso però si può prevedere il valore che y potrebbe assumere in corrispondenza di xo.

Un esempio clinico di tale previsione, è la previsione del valore energetico di soglia Eo,con cui un dato recettore risponde ad una stimolazione di potenza W (energia/tempo) e durata T, quando la durata è zero. Dato che il valore di Eo (=W.T), cambia al cambiare della durata T dello stimolo, si misura la soglia per diverse durate T successivamente decrescenti. Si osserva che quando T diventa sempre più piccolo (tende a zero )il valore di Eo=W.T tende ad avvicinarsi ad un valore costante Eo'.

La possibilità di effettuare una tale previsione, può esprimersi dicendo che Eo' è il limite di Eo quando T tende a 0, ed in forma sintetica con l'espressione

lim Eo = Eo'

^T>0

In generale in una funzione y=f(x), esiste un valore limite yo di y quando x "tende" ad un valore xo (anche esterno al campo di esistenza) se:

i valori successivamente assunti da y per valori di x sempre più vicini a xo, permettono

di prevedere il valore yo che y avrebbe quando x=xo (fig 1). Si scrive

yo = lim _{x> xo} f(x)

Il limite di y non esiste o comunque non possa essere previsto quando x tende a xo, quando

Avvicinandosi x al valore di xo, il valore di y oscilla tra infiniti valori

C'è limite in x=2 e x=8 non c'è limite in x=0

Regole sui limiti

somma: lim _{x> xo} [f(x) f1(x)] = lim _{x> xo} f(x) lim _{x> xo} f(x)

prodotto lim _{x> xo} [f(x) f1(x)] = lim _{x> xo} f(x) lim _{x> xo} f(x)

quoziente lim _{x> xo} [f(x) / f1(x)] = lim _{x> xo} f(x) / lim _{x> xo} f(x)

NB : nel calcolo dei limiti è importante il concetto di aprossimazione :

es: nella funzione y= 1+sen a per a che tende a zero sen a tende ad a

nella funzione

ln (e^x +5) ln e^x x

lim _x> f tende a lim _x> f lim _x> f

f- Si dice che una funzione y=f(x) è continua in xo se per x eguale ad xo, se il valore previsto per y in x=xo (il limite) è eguale al valore assunto da y per x eguale ad xo

lim _{x> xo} f(x) = f(xo)

g- Una funzione è discontinua (prima specie) se per un valore xo , in cui la funzione non è definita , esistono però due valori del limite: per valori di x maggiori di xo e minori di xo

FUNZIONE DERIVATA: la rapidità di variazione

La dipendenza di una grandezza Y da una grandezza X, implicita che cambiando X cambia conseguentemente Y. Per un comodità di scrittura indichiamo col simbolo D la differenza tra due valori di una variabile: y1-y2 = Dy . ( y1= y2 +Dy ).

Dalla relazione operativa y=f(x)

posto x=x1 si ricava y1= f(x1)

x=x2 '' y2= f(x2)

e quindi al variare di x da x1 a x2

x2 = x1+Dx

Dy= y2 -y1 =f(x2)- f(x1) = f(x1+Dx)-f(x)

Es : l'andamento della derivata esprime graficamente la pendenza della curva che rappresenta la funzione:

Se manteniamo sempre eguale la variazione di x , la variazione di y , Dy, dipende dal valore di x in cui è considerata, ossia è funzione di x e di Dx.

Lo stesso avviene per il rapporto tra le due variazioni:

F(x, Dx) = Dy / Dx

Tale funzione rappresenta la rapidità di variazione della variabile y al variare di x, media nell'intervallo Dx. Se consideriamo Dx così piccolo da non poter essere 'numerato'(dx) ,altrettanto piccolo diventa Dy (dy) e la rapidità di variazione si può considerare istantanea, e quindi solo funzione di x. In questo caso la funzione F prende il nome di funzione derivata

Dy = dy/dx

Il calcolo di tale funzione è abbastanza semplice, se si fanno i seguenti passi successivi:

1-Sostituire il simbolo xo nella relazione y=f(x); f(xo)

2-Sostituire il simbolo xo+Dx '' ; f(xo+Dx)

3-Fare la sottrazione dei due termini

4-Dividere per Dx

5-Svolgere le eventuali operazioni, ponendo Dx trascurabile

Es: y= x²

1- f(xo) = xo²

2- f(xo+Dx) = (xo + Dx)²

3- Df = (xo + Dx)² - xo²)

4- Df/Dx = (xo + Dx)² - xo²) / Dx

= ( xo² + 2xo. Dx + Dx² - xo²) /Dx = 2 xo + Dx 2xo

Regole di derivazione (usiamo il simbolo D_x per l'operazione di derivazione dispetto a x) :

somma di due funzioni D_x (f1 f2) = D_x f1 D_x f2

prodotto D_x (f1 * f2) = f2* D_x f1 + f1 * D_x f2

divisione D_x (f1 / f2) = (f2* D_x f1 - f1* D_x f2)/ f2²

funzione di funzione D_x f1(f2(x)) = D_f2 f1 * D_x f2

derivate delle funzioni di base

funzione derivata

Derivate parziali

Una funzione y = f( x1, x2, .xn) di n variabili indipendenti , ha n indipendenti modalità di variazione. La sua variazione totale sarà allora la somma delle sua variazioni al variare di x1, di x2.di xn . Se consideriamo le n variazioni dx1,dx2.dxn delle n variabili, la variazione totale di y sarà:

dy = (D_x1 y) * dx1 + (D_x2 y )* dx2... (D_xn y) *dxn

es : y = x2 + cos (z) ; dy = (2x )* dx + (-sen z)* dz

Le n derivate (D_xi y) per i che va da 1 a n, sono dette derivate parziali.

La variazione totale dy è il differenziale di y

Derivata di un vettore

Molte grandezze fisiche vettoriali (velocità,accelerazione, forza.), sono ottenibili come derivate di altre grandezze vettoriali. Ad es la velocità è la derivata della posizione nel tempo.

L'operazione di derivazione è un'operazione lineare, che si applica a tutte le componenti del vettore originario. Se P è il vettore posizione P(x,y,z) la sua derivata temporale nella base ortonormale i,j,k è:

v = dP/dt = d(xi+yj+zk)/dt = dx/ dt i +dy/dt j+ dz/dt k

Se dP è lo spostamento infinitamente piccolo del punto su una linea s in un punto P dove T è il versore tangente ed n il versore normale alla linea in quel punto, si può esprimere dP nella forma di prodotto tra modulo ds e versore T . La velocità sarà allora

v = dP/dt =d (ds T) /dt = ds/dt T

e l'accelerazione

a= d²s/dt² T + ds/dt dT/dt

Per calcolare il termine dT/dt, osserviamo la figura a)

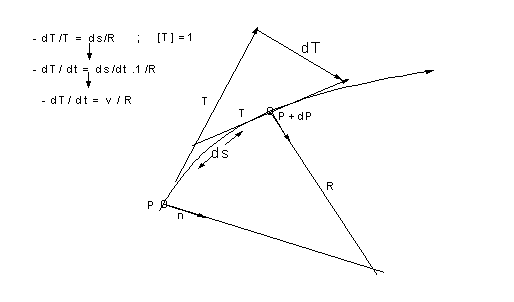
Fig a): al limite per dP molto piccolo,il modulo di dP diventa eguale all'arco ds. La variazione dT/dt è allora data dal rapporto tra il modulo della velocità v ed il raggio di curvatura R diretto secondo la normale n alla curva

L'accelerazione nella sua forma più generale, è data dalla somma di due termini, uno relativo al cambiamento del modulo della velocità ed uno relativo al cambiamento di direzione

a= d²s/dt² T + ds/dt v/R n = dv/dt T + v2/ R n

Operatori vettoriali

Spesso , nei sistemi estesi, una grandezza scalare F ha una variazione continua nelle tre direzioni dello spazio [ temperatura T(xyz), potenziale elettrico V(x,y,z) ecc]. La rapidità di variazione nello spazio di tale grandezza è esprimibile con un vettore ad essa applicato: il suo gradiente:

GRAD(F) = dF/dx i + dF/dy j + dF/dz k c)

che può vedersi come il vettore GRAD moltiplicato per lo scalare F

GRAD F = [d /dx i + d /dy j + d /dz k] F c)

Un altro operatore importante è la divergenza di un vettore V (Vx, Vy, Vz)

(prodotto scalare del gradiente per il vettore)

DIV (V) = [ dVx /dx + d Vy /dy + d Vz/dz]

che esprime la variazione delle componenti lungo le relative direzioni

Uso della derivazione nella soluzione di problemi

a)- valutazione dell'andamento di una funzione y=f(x) di variabile x ,in corrispondenza ad un dato valore xo di x.. Indichiamo con dx la variazione da xo e con dy la corrispondente variazione di y. Si indica l'andamento come:

crescente se per dx>0 dy>0

decrescente se per xo+dx<0 dy<0

massimo se dy>0 per dx<0 e dy<0 per dx>0

minimo se dy<0 per dx<0 e dy>0 per dx >0

flesso se la curvatura (v. raggio di curvatura) cambia segno

Modalità di valutazione

-Si fa la derivata-

-si sostituisce in questa il valore xo

-si analizza il segno del valore numerico risultante:

se negativo ..> decrescente

se positivo ...> crescente

se zero.... > massimo o minimo o flesso

in questo caso si fa la derivata seconda. Se

maggiore di 0 ..> minimo

minore di 0 ..> massimo

eguale a zero..> flesso

es: y= x² dy/dx = 2x

x=-1 decrescente

x= 1 crescente

x=0 massimo, minimo o flesso

d²y/dx² = 2 ...> minimo

b)-determinazione di un valore incognito (parametro noti i punti di massimo o di minimo

Se una funzione di x è "modulata" da un parametro incognito (famiglia funzionale), ed in una misura si conosce il valore xo per cui essa ha un massimo o un minimo, è possibile trovare il valore numerico del parametro stesso.

Modalità di esecuzione

Si esegue la derivazione

Si eguaglia a zero la funzione ottenuto

Si sostituisce alla variabile x il valore xo

Si ricava il valore del parametro

Es: y= 2x²+ax; Minimo per x=1

dy/dx = 4x+a ;

per x=1 .. 4+a=0...> a=--4

Es nella curva da carico in seguito ad ingestione di glucosio, l'andamento temporale della concentrazione di glucosio nel sangue può essere rappresentato dalla funzione

G=go + g1.e^-kt sen (wt)

Supponendo noto w, il valore di k può essere ricavato se si conosce un valore to di t in corrispondenze del quale G ha un massimo o un minimo. La derivata della precedente è

Dalla

dG/dt = g1. [ -k. e^-kt sen (wt) + w. e^-kt cos (wt)] = 0 si ha

-k sen (wt) + w. cos (wt)=0 ossia k = w/ tang (w)

Interpolazione.Minimi quadrati

Supponiamo che in uno studio sulla dipendenza del valore di una grandezza y da una grandezza x, pur conoscendo le regole operazionali che collegano y ad x, non siano noti i valori dei parametri a1-ak . Il fenomeno sia in teoria descritto dalla

y= f(x,a1,a2..ak)

Se la k-upla ai fosse nota, dato che nella misura è presente sempre un certo errore, per una coppia di valori xi ,yi, il valore y calcolato da xi e il valore misurato yi non coincidono esattamente, ma tra loro esiste uno scarto ei:

e_i = y-yi =f(xi,a1,a2.ak)-yi

Il metodo dei minimi quadrati consiste nell'ipotesi che, quando i parametri siano incogniti, i loro valori corretti sono quelli che minimizzano la somma dei quadrati degli scarti ei:

_i=1,n

E(a1,a2..an) = S e_i² = S_i (f(xi,a1,a2.an)-yi) ²

La condizione di minimo della funzione E a più variabili, si esplica nell'annullamento delle

K derivate parziali dE/dai. La soluzione del sistema di k equazioni e k incognite così ottenuto fornisce i valori più probabili dei k parametri

Il metodo diventa semplice se i parametri compaiono in forma lineare. Es sia:

y=ax+b ; E(a,b)= S (a.xi+b-yi) ²

dE/da = S xi . (a.xi+b-yi) =0 ; dE/db = S (a.xi+b-yi)

a.S xi² + bS xi = S xi.yi ; a.S xi + n.b = S .yi

EQUAZIONI DFFERENZIALI

Si intende per equazione differenziale un'equazione , comprendente :

una variabile, le sue derivate rispetto ad un'altra variabile fino all'ordine n, e termini numerici o funzione della variabile stessa:

(y,dy/dx, d²y/dx²,.., dⁿy /dxⁿ ,f(x),a,b.)=0

L'ordine dell'equazione è l'ordine della massima derivata che vi compare.

La soluzione consiste nel ricavare la funzione/i y(x) che soddisfa all'equazione, note almeno n coppie di valori numerici x,y corrispondenti (condizioni iniziali o al contorno)

1-esempi

Nello studio di fenomeni in cui lo stato del sistema varia nel tempo (o nello spazio), è importante ricavare una previsione del valore di una data grandezza ad un tempo (in un punto) prefissato, nota l'evoluzione di questa in un tempo (un intervallo spaziale) brevissimo ed il valore numerico di tale grandezza in un istante prefissato (una data posizione)( ad es. all'inizio dell'osservazione)

a)Si voglia conoscere il numero N1 di individui a cui arriva ad un dato tempo t1 la numerosità di una popolazione, che parte inizialmente (a t=0) da un numero No di soggetti.

In ragionamento che si segue è:

1- si sceglie un tempo generico t

2-si considera un intervallo successivo "molto breve" del tempo Dt,

3- in tale intervallo l'aumento DN del numero di individui sarà molto piccolo

4- nell'intervallo DT,il numero di "nati" DN dipenderà dal numero di individui N presenti

al tempo t e dal valore di DT :

1) DN = k.. N. DT

Analogo problema, si può presentare nella stima del valore di una grandezza di stato, il cui valore dipende dalla posizione , quando si voglia conoscere il valore che essa assume ad una distanza X da una posizione iniziale nota.

b) Un gas in equilibrio per cui valga la legge di Boyle per la relazione tra pressione P volume V, temperatura T e numero di moli n : P =nRT/V. Introducendo la densità d (massa /volume) si ha che

P==RTd/ M ossia d = P.M/RT (M peso molecolare). L'equilibrio delle forze agenti porta alla relazione tra la forza peso e le forze dovute alla pressione interna

d.g. dS.dh + dP.dS =0 che si riduce a dP/dh = - d.g = - P .Mg/RT

ossia ad una relazione tra quota e pressione del tipo

dP/P = - (Mg/RT) .dh 2)

c)Si voglia conoscere il numero N1 di soldati che riescono a superare una distanza X1 in un campo minato, sapendo che il numero di quelli che vi entrano (a X=0) è No:.

In ragionamento che si segue è:

1- si sceglie una generica distanza X dall'ingresso

2-si considera un intervallo successivo "molto breve" DX,

3- in tale intervallo il numero di soldati diminuisce di una quantità DN molto piccola

4- nell'intervallo DX,il numero di morti DN dipenderà dal numero di individui N presenti alla

distanza X e dal percorso DX

DN = - k.. N. DX 3)

Nel caso 1) e 2) il numero N è una funzione rispettivamente del tempo N(t) e della distanza, ed il problema da risolvere ,è quello di trovare la relazione che lega N a t, ossia la "forma" della funzione.

La 1) e 2) sono equazioni in cui le variabili compaiono come "differenze":Dt, DX, e sono dette perciò equazioni alle differenze o differenziali

Sia 1) che 2) si possono risolvere in modo approssimato con un processo iterativo

Es 1):

si divide l'intervallo t1 in n intervalli eguali DT

DN1 = k.No.Dt > N1 = No + k.NoDt

DN2 = k.N1.Dt > N2 = N1+ k.N1.Dt = No +kNoDt + k.(No+k.No.Dt).Dt=

No [ 1 + 2k Dt + (k.Dt)2 ] *)

Ecc,ecc

Tale processo, che termina nell'intervallo n^esimo è però approssimato, e diventa tanto più preciso quanto Dt è più piccolo, e conseguentemente il numero n di intervalli(t1/Dt) più grande. La soluzione si ottiene quindi facendo il limite della somma *) per Dt tendente a zero.

Questa lunga procedura si può evitare, utilizzando i concetti di derivata ed integrale.

FUNZIONE INTEGRALE

Sommatoria

Quando si debbono sommare n grandezze dello stesso tipo, ma di valore numerico diverso, si ricorre spesso all'espressione

_i=1,n

S_i x i = x1 + x2 +...xn

La sommatoria si usa molto spesso, nel caso di funzioni qualitativamente simili, ma diverse nei parametri a,b.

_i=1,n

S f (x, ai,bi.)

Ad esempio, n sinusoidi di diverse ampiezze Ai e pulsazione wi multipla di un valore base w : wi= i w dove i=1.n

_i=1,n

S Ai sen (i w ) = A1 sen ( w ) + A2 sen (2 w )+ ... An sen (n w )

Lo sviluppo precedente, può applicarsi anche alla somma dei valori di una funzione di una variabile x, calcolati per xi valori della variabile.

Supponiamo che i valori xi siano calcolati in un intervallo xf-xo . Dividiamo l'intervallo in n intervalli eguali Dx= (xf-xo)/n .Il valore i-esimo xi sarà allora xi =xo+i Dx

La somma dei valori corrispondenti f(i Dx ) sarà

_{i=0,n-1 i=0,n-1}

S f(xi ) = S f(xo +i Dx )

I valor medio di questa espressione sarà

_{i= 0,n-1}

S f(xo+ i Dx) / n

Moltiplicando sopra e sotto per Dx, al denominatore abbiamo la lunghezza dell'intervallo

Nel caso che Dx diventi così piccolo da non essere numerabile , il numero n degli elementi della sommatoria diventa enormemente grande (tende all'infinito),ed il valore f(xo+idx) corrisponde al valore di f corrispondente al generico valore di x nell'intervallo. La precedente allora diventa la media della funzione nell'intervallo xf-x0

_{i= 0,n-1}

Media f(x)_xo,xf= 1/(xf-xo) lim _Dx>0 [ S f(xo+ i Dx) Dx ] .

Il valore limite dalla sommatoria è indicato con una s allungata ai cui estremi è specificato l'inizio e la fine dell'intervallo in cui la somma è fatta:

xf

Media = 1/ (xf-xo) . f(x) dx

xo

Nell'espressione

xf

f(x) dx b)

xo

supponiamo che esista una funzione F(x) tale che la sua derivata rispetto ad x sia la funzione data f(x)

f(x) =d F(x)/ dx si ha f(x) dx =d(F(x)) c)

poiché la somma degli elementi dà l'intero,e DF rappresenta l'intervallo DF= (F(xf)-F(xo)) /n

_{i= 1,n}

S   DF = n DF = F(xf )- F(xo)

La precedente vale qualunque sia n, per cui, nel caso valga la c) la b) diventa 

xf

f(x) dx = F(xf)- F(xo)

xo

L'operazione precedente é detta somma integrale o integrale definito di f(x) nell'intervallo xf-xo. Nel caso che l'estremo xf sia un valore x variabile

x

f(x) dx = F(x)- F(xo)

xo

in tal caso la somma è data da una funzione di x F(x) definita a meno di un termine costante.

Se l'estremo F(xo) non è noto, la precedente si indica semplicemente con

f(x) dx

l'integrale indefinito, di f(x) calcolato dalla funzione F(x) ( "primitiva" di f(x)) a meno di una costante additiva. Poiché per l'intervallo x di una variabile

d x = x > d = 1

L'operazione è quindi l'operazione inversa alla variazione d.

Il fatto che l'integrazione sia inversa alla derivazione, permette di calcolare tale funzione, note le derivate delle funzioni elementari e non.

Ad es

sen(x) dx

Si cerca la funzione che derivata rispetto a x, dia sen(x)). Questa esiste ed è -cos(x)

I(sen(x)) = -cos(x) +cost

Regole di derivazione principali:

I [f(x) f1(x)] = I f(x) I f1(x)

I[ f(x) d(f1(x)] = f(x).f1(x)- I[f1(x).d(f(x)] dalla regola del prodotto

d( f(x) .f1(x)) /dx = f(x) d f1(x)/dx + f1(x) df(x)/dx

I[ f(cx)] = 1/c [f (z)] ponendo z=c.x se c è costante

SOLUZIONE EQUAZIONI DIFFERENZIALI col calcolo integrale

Il calcolo integrale è utilizzato molto in geometria per valutare aree e volumi.Anche se non di grande interesse per il campo medico, consideriamo ad esempio il calcolo dell'area del cerchio

Consideriamo una corona circolare di raggio r<R e di ampiezza dR. Se dR è infinitamente piccolo, l'area della corona può essere espresso da

dA =2p r. dr

Integrando entrambi i membri, per r da R a 0

R

A= p r. dr = 2p R²/2 =p R²

Riprendendo gli esempi 1)2)3) del paragrafo precedente, la soluzione delle tre equazioni è semplice operando con l'intergrazione da entrambi i lati dell'eguaglianza:

DN/N = kDt ; dP/P = - (Mg/RT) .dh ; DN/N = -k.Dx

Si considera poi DN infinitamente piccolo dN, e si applica ad entrambi i membri, l'operazione di integrazione (somma)

DN/N = kDt ; dP/P = - (Mg/RT) .dh ; DN/N = - k.Dx

Risolvendo con regole note

Ln N - ln No= k t1 ; Ln P - ln Po= Mg/RT .h ; ln N - ln No = -k x1 con brevi passaggi

N = No e ^k.t1 ; P = Po. e ^h.(Mg/RT) ; N= No e ^-k.x1

Osserviamo che le equazioni 123 coinvolgono le due variabili e le loro derivate, ossia fanno parte della classe generale delle equazioni,:

F(y(x),Dy/dx,d2y/dx2 ..)=0

in cui l'incognita è una funzione di variabile di cui si deve determinare la natura. La soluzione di tali equazioni avviene sempre per integrazione ed in alcuni casi può richiedere calcoli complessi.

Tra le equazioni di più facile soluzione sono le equazioni differenziali lineari. Indicando per semplicità con D l'operazione di derivazione (D=d/dx), tali equazioni assumono la forma di un polinomio in D, applicato ad y, dove la massima potenza (ordine di derivazione) costituisce l'ordine dell'equazione:

[Dⁿ + a1(x) D^n-1+ a2(x) D^n-2+ an(x)].y(x) = F(x) ordine n

Se F(x)= 0 l'equazione è omogenea

La loro soluzione comprende sempre una somma di n esponenziali. La soluzione è particolarmente semplificata nel caso di coefficienti costanti

Primo ordine [D +k]y =0 > y= yo e ^-k.x

Secondo ordine [D2 + a1 D +a2].y = [ D-c1].[D-c2]y =0 > y= A e ^-c1.x + B e ^-c2.x

Con c1,c2 le due radici del polinomio

In genere per un ordine n qualsiasi

[ D-c1].[D-c2]... [D-cn]y =0 1)

la soluzione è

_i=1,n

S Ai e ^-ci.x 2)

Se la 1) invece di essere eguagliata a zero è eguagliata ad un valore costante F(termine forzante), alla soluzione2) va aggiunto un termine additivo che si ricava dai coefficienti dell'equazione.

Per equazioni non omogenee (le precedenti eguagliate ad una funzione o ad un valore numerico), la soluzione è semplice nel caso che i coefficienti

Per la soluzione esatta di un'equazione differenziale, necessitano tante condizioni iniziali o condizioni al contorno, quanto è l'ordine dell'equazione. Queste sono i valori numerici f(xi) assunti dalla funzione incognita, in corrispondenza ad n valori xi della variabile

Ad es

Dy +2y = 0  (con y=10 per x=0) y= A e ^-2.x > 10. e ^-2.x

Nel caso che ci sia un termine forzante ( nell'esempio precedente F=4)

Dy +2y = 4

a-Sostituendo la soluzione nell'equazione

-2 A e ^-2.x +2.( A e ^-2.x + C) = 4 > C = 2

b-e dalle condizioni iniziali y=10 per x=0

y= A e ^-2.x + 2 > 10 = A+2 > A = 8 e la soluzione è

y= 8 e ^-2.x + 2

APPENDICE

1)NUMERI COMPLESSI

Unità immaginaria : i = -1 per cui i² = 1

Numero immaginario : i a a numero reale

Numero complesso : c(b,a) = b + i a a e b numeri reali

Modulo del nr. Complesso: ( b² + a²)

Complessi e coniugati : c(b1,a1)= b1 + i a1 ; c(b2,a2) = b2 - i a2

Operazioni

Somma di due complessi: c(b1,a1) c (b2,a2) = b1 b2 + i (c1 c2)

Prodotto " : c(b1,a1) (b2,a2) = (b1 b2 - a1 a2) + i (b1 a2 + b2 a1)

divisione : c(b1,a1) / (b2,a2) = [c(b1,a1) (b2,a2)] / (b2,a2) ²

Forma trigonometrica

Si considera il numero complesso come un punto di un piano individuato da un asse reale ad un asse immaginario ortogonali (vedi fig)

Formule di Eulero:

Si dimostra che , utilizzando l'espressione trigonometrica del numero complesso, le funzioni esponenziali a base e (2.71828..) ed esponente complesso i.j sono esprimibili come:

e ^i.j = cos j i.sen j da cui

cos j = (e ^i.j + e ^{- i.j} ) / 2 ; sen j = (e ^i.j - e ^{- i.j} ) / 2.i

2-Definizioni e formule trigonometriche utili:

Definizioni

(tangente ) tan j = sen j /cos j

(cosecante) csc j = 1 / sen j

(secante) sec j = 1 / cos j

(cotangente) cot j = cos j / sen j

Operazioni

sen² j + cos² q = 1 ; sen² j - cos² q = 2 cos j sen j

sen (j q ) = sen j cos q cos j sen q

cos (j q ) = cos j cos q -+ sen j sen q

tan (j q ) = ( tan j tan q ) / ( 1 -+ tan j tan q

3-Limiti notevoli

Riteniamo utili per lo studente riportare alcuni limiti speciali:

lim _{j > 0} ( sen j j

lim _{j > 0} ( 1-cos j j

lim _{x > 0} ( 1 + x )^1/x = e

lim _{x >} ( 1 + 1/x )^x = e

lim _{x >0} ( e ^x -1) / x = 1

lim _{x >0} ( x -1) / ln x = 1

4-Sviluppo di una funzione periodica tramite una serie di funzioni

Supponiamo di effettuare n misure di una grandezza G in intervalli successivi di tempo o ad intervalli spaziali successivi. La sequenza di valori ottenuta G (g1,g2.gn), è un vettore di ordine n. Può essere allora scelta una base ortonormale u1,u2...un, per cui qualunque sequenza Gi è rappresentabile come

_k=1..n

Gi = S ai_k u_{k   1)}

Possiamo osservare che la "coordinata" ai_m si ottiene eseguendo il prodotto scalare tra il vettore Gi ed il vettore u_m della base

_k=1..n

ai_m = Gi x u_m = S ai_k u_k x u_m

Funzione in un intervallo limitato come vettore, sviluppo di Fourier

Sia una funzione y=f(t) è limitata in un intervallo T. Dividiamo T in N intervalli eguali dt=T/N ,e consideriamo i valori di y(i) in corrispondenza agli n valori di t : i.dt con i=0..n-1. Otteniamo in questo modo una sequenza

y(i) = f(i.dt) per i=0.. n-1

Posto w=2p/N scegliamo le sequenze ortogonali:

1/N , 2/N cos (w.i), 2/N sen (w.i), 2/N cos (2.w.i), 2/N sen (2.w.i).. 2/N cos ((N-1)/2.w.i),

2/N cos ((N-1)/2.w.n). La 1) in questo caso si scrive

_1,N-1/2

y(i) = ao+ _k (a_k cos(k.w.i) + b_k sen(k.w.i)) 2)

con

_{0,N-1 0,N-1 0,N-1}

a_o = 1/N _i y(i) ; a_k = 2/N _i y(i) cos(k.w.i) ; b_k = 2/N _i y(i) sen(k.w.i)

Se aumentiamo indefinitivamente il numero N di intervalli (andiamo al limite per N tendente all'infinito) dt diventa infinitesimo , i.dt tende al valore t ed y(i) a f(t).

Se inoltre moltiplichiamo l'argomento del cos e del seno per dt,

nell'espressione k. 2p/N.i.dt/dt

N.dt diventa T ed i.dt diventa t per cui la 2) tende a

_k=1..

y=f(t) = ao + S (a_k cos (k.w.t) + b_k. sen(k.w.t )) 3)

con

_{T/2 T/2 T/2}

a_o = 1/T f y(t) dt ; a _k = 2/T y(t) cos (w.k.t)dt ; b _k = 2/T y(t) sen (w.k.t)dt

-T/2 -T/2 -T/2

La precedente dà lo sviluppo di Fourier per una funzione definita in un intervallo limitato

Essa vale inoltre per qualunque funzione periodica di periodo T, tale cioè che

f(t) = f(t+T)

Molto spesso, si descrive allora una funzione limitata o periodica, con il suo "spettro" in frequenza riportando in funzione di k, i termini P(k):

P(k) = (a²_k + b²_k)