|
|
| |
ALTRI DOCUMENTI
|
||
Quadripoli
Si definisce "quadripolo" qualunque elemento di circuito abbia due coppie di terminali. In pratica, quasi tutto può essere un quadripolo: anche pezzi di cavo o componenti con solo due o tre piedini possono essere utilizzati come quadripoli, ma le forme più comuneme 212f52c nte usate sono due:
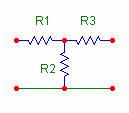
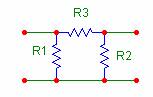
Quadripolo a "T" Quadripolo a "pi greco"
Per ottenere il massimo trasferimento d'energia al carico occorre studiare la resistenza (o, in modo più generale, l'impedenza) vista da entrambe le coppie di terminali. I quadripoli mostrano impedenze diverse dalle due coppie di morsetti, a meno che non siano "simmetrici" : la simmetria, ovviamente, rende uguali le impedenze viste dai due lati.
Z2 (Ω) RL (Ω)
391 0
633 400
800 900
967 1,9k
1056 3 k
1210 10 k
1300 ∞
231 0
475 300
700 600
665 1 k
933 4,7k
1012 10 k
1100 ∞
![]()
![]()
![]()
![]()
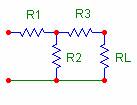
R1 = 100 Ω
R2 = 1 kΩ
R3 = 300 Ω
La prima
tabella è relativa all'impedenza vista dalla prima coppia di terminali al
variare del carico; la seconda tabella riguarda l'impedenza vista dalla
seconda coppia di morsetti al variare del carico. Ma i casi dovrebbero
essere infiniti..
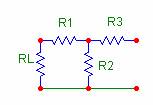
Conviene calcolare l'impedenza con carico 0 e con carico infinito (la prima e l'ultima riga), perché costituiscono i due casi limite; tutti gli altri valori devono risultare interni ad essi.
Se fosse
possibile realizzare le tabelle con un numero enorme di righe, si noterebbe che
una coppia di valori si presenta in entrambe; questo capita sempre, e per una
coppia soltanto. Tali valori sono l'equivalente della risoluzione di un sistema
a due equazioni: ciascuna ha separatamente infinite soluzioni, ma il sistema
consente di trovare la coppia di valori comuni.![]()
Impedenza Immagine
I valori comuni ad entrambe le tabelle si chiamano "impedenza immagine"; hanno la proprietà che, se l'una viene usata come carico, si vede l'altra come impedenza; ma lo vedremo meglio più avanti.
Come calcolare un'impedenza immagine senza dover riempire due colonne di infiniti calcoli? Con questa formula:
![]()
che va applicata ad entrambe la coppie di morsetti:
![]() Zo = impedenza
vista con uscita aperta (carico ∞) sono
i due valori estremi
Zo = impedenza
vista con uscita aperta (carico ∞) sono
i due valori estremi
Zcc = impedenza vista con uscita in corto (carico nullo) della tabella
Se il quadripolo è simmetrico, basta applicarla una volta sola; in tal caso, l'impedenza immagine viene chiamata "impedenza caratteristica".
1) Calcoliamo l'impedenza immagine in questo caso:
R1 = 100Ω Zi1= R2 = 20 Ω R3 = 200 Ω Zi2 = ![]()
![]()
porta 1
![]() = 119 Ω
= 119 Ω![]()
![]() = 218 Ω
= 218 Ω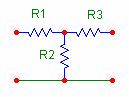 porta
2
porta
2
Se mettiamo un carico di 218 sulla porta 2, dalla porta 1 si vedono 119
Se mettiamo un carico di 119 sulla porta 1, dalla porta 2 si vedono 218
Calcoliamo l'impedenza caratteristica in questo caso:
R1 = 300 Ω Zc = R2 = 120 Ω
![]() = 403 Ω
= 403 Ω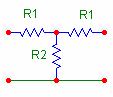
Mettendo un carico di 403 Ω su una delle porte, dall'altra si vedono 403
Come si progetta un quadripolo simmetrico con impedenza caratteristica nota?
Conviene scegliere il valore di una delle resistenze in modo che sia circa la metà dell'impedenza caratteristica che si vuole ottenere, o comunque inferiore ad essa. Poi si applica la formula . Vediamo un esempio: Progetta un quadripolo simmetrico con Zc = 400
![]() =
= ![]() =
= 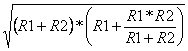 =
= ![]() =
= ![]()
Scelgo R1 = 220 Ω: 400 = ![]() Elevo al quadrato:
Elevo al quadrato:
160000 = 48400 + 440 * R2 111600 = 440 * R2 R2 = 254 Ω
Il progetto è più complesso se le impedenze immagine si riferiscono ad un quadripolo asimmetrico: in tal caso, le resistenze da trovare sono tre, e l'unico modo per farlo è fissare il valore di una resistenza e applicare la formula ad entrambe le coppie di morsetti, risolvendo il sistema che ne consegue.
Adattamento
Lo studio delle impedenze immagine è finalizzato al massimo trasferimento di potenza al carico. Per avere questo risultato, occorre che il segnale che giunge sul carico non subisca un effetto di riflessione, perché è ovvio che il segnale riflesso non viene utilizzato e quindi limita il rendimento del circuito.
La riflessione viene eliminata solo se la resistenza interna dei generatori, l'impedenza in ingresso e in uscita dei vari elementi, l'impedenza caratteristica dei cavi di collegamento e, infine, il carico, hanno lo stesso valore. In tal caso, si lavora in regime di perfetto adattamento.
In particolare, la rete di telefonia fissa utilizza generatori normalizzati con resistenza interna di 600 Ω, doppini telefonici (Zc = 600 Ω), apparati di centrale con impedenza di 600 Ω, gli apparecchi usati dagli utenti dovrebbero essere a 600 Ω e le derivazioni non devono porre i telefoni in parallelo perché se ne dimezza l'impedenza totale.
Decibel
Il decibel (dB) è un modo di indicare varie grandezze fisiche: consiste nel calcolarne il logaritmo decimale e moltiplicarlo per 20.
Esempio: se una tensione è di 1000 V, calcolata in dB sarà: 20 Log 1000 = 60 dB.
Attenzione: l'espressione di una potenza in dB prevede di moltiplicare per 10, non per 20, il logaritmo decimale (P = V2/R ; P = R I2 ; la tensione e la corrente vi sono contenute al quadrato, per la regola dei logaritmi l'esponente diventa un fattore moltiplicatore e si ottiene il 20..).
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025