PROVA DI LABORATORIO DI SISTEMI - A cosa serve la Correlazione?

c)  Sistemi di compressione di segnali, per la verifica di periodicità dei segnali attraverso spostamento e confronto di un unico segnale.

Operatore di Correlazione:

Dati due segnali reali S1(t) e S2(t), non periodici, la funzione di correlazione è così definita:

L'operatore di correlazione confronta i due segnali attraverso il loro prodotto. Nel caso che le due funzioni siano molto simili, il prodotto darà una funzione simile ad una potenza istantanea. L'integrale risultante assumerà un valore molto elevato. Il confronto tra i due segnali può anche essere fatto traslando uno dei due di un valore pari a "t

Nella correlazione R t : i pedici indicano il numero delle due funzioni da confrontare, mentre l'argomento definisce il valore della traslazione fra le due funzioni.

Nel caso in cui le due funzioni sia uguali fra loro si parlerà d'autocorrelazione e tale funzione sarà data da

In cui RS t è appunto l'autocorrelazione e t il valore di traslazione o di ricerca della correlazione. Il valore più grande dell'autocorrelazione RS t si otterrà per t . Questo perché RS coincide con l'energia del segnale.

Consideriamo ora come avviene la correlazione e l'autocorrelazione attraverso alcuni grafici ed esempi:

Inseriamo questi valori per creare ben tre tipi differenti d'onda.

SEGNALE UNO

Ampiezza 1 :    0.8 Ampiezza 2 : 0.6 Ampiezza 3 : 0.4

Frequenza 1:    100 Frequenza 2 : 200 Frequenza 3 : 300

SEGNALE DUE

Ampiezza 1 :    0.1 Ampiezza 2 : 0.2 Ampiezza 3 : 0.5

Frequenza 1:    1000 Frequenza 2 : 100 Frequenza 3 : 500

SEGNALE TRE

Ampiezza 1 :    0.2 Ampiezza 2 : 0.3 Ampiezza 3 : 0.4

Frequenza 1:    100 Frequenza 2 : 200 Frequenza 3 : 300

Notare la lieve somiglianza tra il SEGNALE UNO e il SEGNALE TRE

Bene, passiamo alla correlazione visiva. L'onda in GRIGIO corrisponde al segnale immesso, mentre l'onda in VERDE corrisponde al segnale correlato.

PRIMO SEGNALE con PRIMO SEGNALE (o meglio definito AUTOCORRELAZIONE)

"Notare cosa succede nel caso che due segnali identici si correlino (AUTOCORRELAZIONE)."

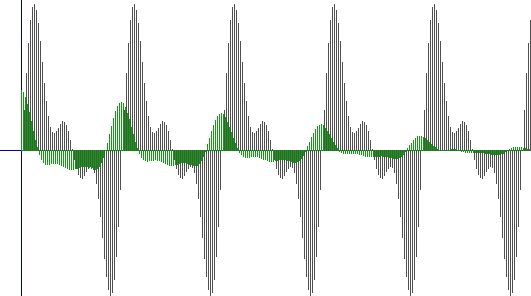
PRIMO SEGNALE con SECONDO SEGNALE

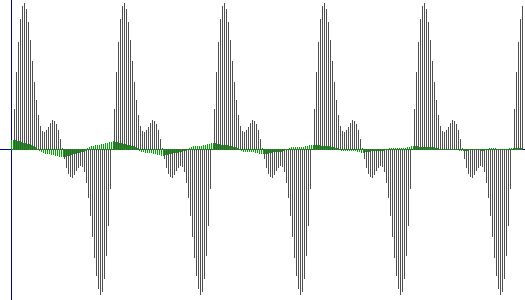
PRIMO SEGNALE con TERZO SEGNALE

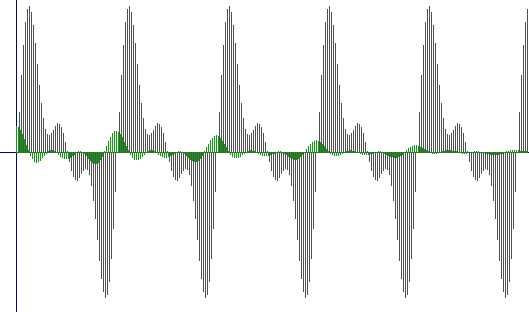
CONCLUSIONI : Analizzando i vari segnali d'uscita notiamo che la correlazione è avvenuta in modo più evidente tra il primo segnale e se stesso. Infatti se controllassimo la media della correlazione tra il segnale 1 e se stesso noteremo che è molto più elevata delle altre due, e questo ci potrebbe assicurare quasi totalmente che la correlazione più precisa è avvenuta per il primo caso. Però esistono delle eccezioni.

Che cosa succederebbe se provassimo a correlare il TERZO SEGNALE per gli altri? Guardate i grafici:

TERZO SEGNALE con PRIMO SEGNALE

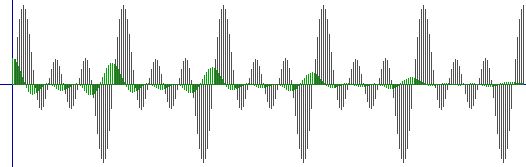
TERZO SEGNALE con SECONDO SEGNALE

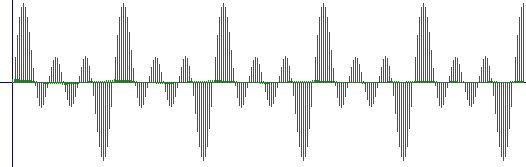
TERZO SEGNALE con TERZO SEGNALE (AUTOCORRELAZIONE)

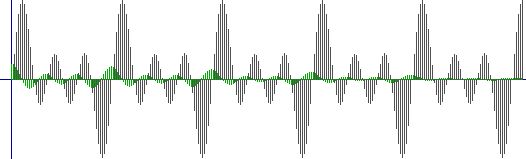
CONCLUSIONE CASO SPECIALE : Dato che ci aspettavamo che, come nel primo caso citato prima, l'autocorrelazione fosse la cosa più ovvia, guardando i grafici qua sopra noteremo che:

Il TERZO SEGNALE correlato con IL PRIMO produce un segnale di correlazione molto simile a quello del TERZO SEGNALE con il TERZO SEGNALE (l'autocorrelazione).

A questo punto potrebbero venirci dei dubbi su quale segnale avevamo deciso di correlare. Noi volevamo proprio correlare il terzo, sicuri che l'autocorrelazione ci avrebbe arrecato ancora vantaggio. Invece in questo caso speciale, dato l'estrema somiglianza delle sinusoidi, già ad occhio notiamo che la correlazione è avvenuta per il TERZO SEGNALE con il PRIMO SEGNALE. Se ancora non fossimo sicuri di questo potremmo controllare la media. Effettivamente la media più alta risulta proprio per la prima correlazione. In questa maniera dimostriamo che la correlazione a volte può avvenire anche per casi diversi da quelli che ci aspettiamo.

CODICE SORGENTE DEL PROGRAMMA

TXT: AUTOCORRELAZIONE & CORRELAZIONE

#include <stdlib.h>

#include <stdio.h>

#include <conio.h>

#include <math.h>

#include <graphics.h>

#include <dos.h>

#include <iostream.h>

#include <complex.h>

static const double FC = 10000;   /*10 KHz Frequenza campionamento */

static const float TC = 0.0001;   /*campionamento in secondi */

static const int Ns = 3; /* 3 Segnali */

static const int Nh = 512;    /*campionamento ingresso */

static const float Pi = 3.141592; //Pi greco

float S[Ns][Nh];   //Campionamento segnali

float R[Ns][Nh];   //Correlazioni

int x; //Segnale incognito

int n;

// Inizializzazione Procedure varie

void assi(int j, int x);   // Stampa Grafico

void produzione_segnale();  // Genera Segnali

void Correlazione(int x); // Correlazione tra segnali

void menu2();   // Menu di scelta 1^,2^,3^ Onda

void main()

}

while (fine);

// INIZIO VOID CREA SEGNALI

void produzione_segnale()

// ** ** *

}

// FINE VOID CREA SEGNALI

// INIZIO CORRELAZIONE SEGNALI

void Correlazione(int x) // Viene passato il segnale da Correlare

// Inserisco il valore trovato nel vettore

// che poi verr. stampato a video

R[j][n]=somma/Nh;

}

assi(j,x); // Chiamata alla void di stampa a video

}

// FINE CORRELAZIONE SEGNALI

// INIZIO MENU DI SCELTA SEGNALE DA CORRELARE

void menu2()

}

while (fine);

// FINE MENU 2

// INIZIO VOID DI STAMPA GRAFICO E ONDE

void assi(int j,int x)

setcolor(1);

xmax = getmaxx();

ymax = getmaxy();

/* draw a retta linea da Sx a DX*/

line( 0, ymax /2, xmax, ymax / 2);

/* draw a retta line dall'UP al DOWN*/

line (xmax / 8, 0, xmax / 8, ymax);

setcolor(3);

// Scorro tutto il vettore per stamparlo man mano, creando una riga per

// ogni valore. Il "*100" presente verso la fine del comando LINE serve

// solo per poter visualizzare un onda abbastanza grande. Come lo ZOOM.

for ( n = 0; n < Nh ; n+=2)

/* clean up */

getch();

closegraph();

// FINE VOID DI STAMPA GRAFICO E ONDE