|
|
| |
Loran-C
e
GPS

Studiando la Teoria della Relatività mi sono reso conto di come le varie formule che questa teoria propone apportino sensibili variazioni alle formule della fisica classica solo se stiamo studiando problemi in cui si debbano considerare velocità molto alte, confrontabili con la velocità della luce. Per questo motivo volevo vedere se esistessero situazioni più vicine alla vita comune che fossero in qualche modo legate al Principio di Relatività; tutto questo l'ho trovato, come si vedrà in seguito, studiando i due sistemi Loran-C e GPS.
Il lavoro che ha portato alla stesura di questa ricerca si è diviso in due parti: una parte riguardante la ricerca delle informazioni relative ai due sistemi; ed una relativa ai calcoli per gli esempi dei Cap. 3.5 e 4.5. Per la prima mi sono servito sia di testi di fisica che di articoli (vedere Cap. 5), integrando le informazioni da essi ricavati con altre trovate sulla rete Internet. Per la seconda ho utilizzato dati ricavati dal testo "SPAZIOTEMPO: la relatività ristretta" di R. Sexl e H. K. Schmidt e dal testo "INVITO ALLA FISICA" Vol. 3 di P. A. Tipler.
Fin dalla sua prima formulazione nel 1905 la teoria della relatività proposta da Einstein venne criticata da buona parte del mondo scientifico del tempo. Il perché di tutto ciò è comprensibile se consideriamo che questa teoria si oppone radicalmente alla visione del mondo che gli uomini hanno sempre avuto. Infatti con la relatività viene meno l'idea di un tempo e di uno spazio assoluti e si introduce l'idea di uno spazio quadridimensionale (tre dimensioni spaziali ed una temporale) nel quale noi viviamo.
La diffidenza di molte persone riguardo a questa teoria è alimentata anche dal sorgere di paradossi (come quello dei gemelli) che derivano però da una non perfetta applicazione dei principi propri della teoria stessa.
Oggigiorno questa critica contro 545d33f la relatività si è più placata anche per il fatto che essa è confermata da molti esperimenti (esperimento di Hafele-Keating; esperimenti con le particelle elementari; etc.) e sta entrando nella tecnologia. Il Loran-C e il GPS sono proprio due delle applicazioni della teoria della relatività alla tecnologia.
Il Loran-C (Longe Range Aid to Navigation) è un sistema di navigazione che permette ai vari utenti di conoscere la loro posizione, basandosi sulla ricezione di segnali inviati da appositi trasmettitori. In particolare un sistema come il Loran-C viene definito "iperbolico" per il fatto che sfrutta il principio secondo il quale la differenza di tempo tra i segnali in arrivo da due trasmettitori tra loro sincronizzati, in un certo punto, è proporzionale alla differenza delle distanze tra i due trasmettitori e il punto suddetto. Il luogo dei punti aventi stessa differenza di tempo da uno stesso paio di trasmettitori è un'iperboloide (chiamata LOP) che ha come fuochi i due trasmettitori.
Ogni trasmettitore Loran emette impulsi che hanno un periodo tipico del trasmettitore stesso (detto GRI) che permette quindi all'utente di identificare da quale stazione sta ricevendo il segnale; inoltre tutti i trasmettitori sincronizzati che hanno un medesimo GRI vengono definiti Catena.
Ogni Catena è composta da un trasmettitore principale (detto Master) e da almeno due trasmettitori secondari (detti Slave).
La stazione principale di ogni Catena è identificata con la lettera M, mentre quelle secondarie si indicano con le lettere W, X, Y, e Z. Quindi ogni coppia Master-Slave (X) verrà designata con la sigla MX e la differenza di tempo ad esse associata verrà detta TDX (considerando che ogni LOP ha una differenza di tempo, detta appunto TD, costante).
Per localizzare un punto è necessario determinare due TD che determinano due LOP; intersecando queste due LOP è possibile determinare il punto P in cui l'utente si trova (Figura 1.1).
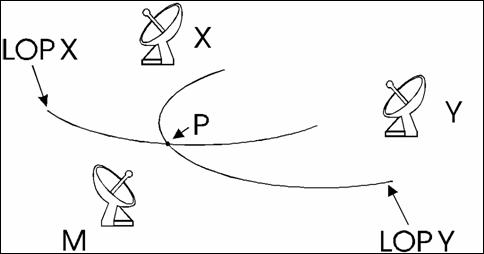 Fig. 1.1
Fig. 1.1
Tutte le stazioni trasmittenti Loran sono
equipaggiate con orologi atomici (basati sulle oscillazioni di atomi di cesio)
che hanno un alto grado di precisione (l'errore è dell'ordine di 5![]() 10-7 s). Nonostante questo è possibile che essi
abbiamo comunque dei problemi oppure che vi siano problemi nella trasmissione
dei radiosegnali; tutto ciò può causare la variazione della TD associata ad una
data coppia di trasmettitori, e questo causerebbe un errore nella
determinazione del punto in cui il ricevente si trova. Per evitare problemi di
questo tipo sono presenti sul globo delle stazioni SAM (System Area Monitor).
Esse sono costituite da ricevitori Loran che controllano la TD di una
determinata coppia Master-Slave; se la TD in questione non è costante queste
stazioni di controllo o provvedono a correggerla, oppure avvisano gli utenti
del non perfetto funzionamento del sistema.
10-7 s). Nonostante questo è possibile che essi
abbiamo comunque dei problemi oppure che vi siano problemi nella trasmissione
dei radiosegnali; tutto ciò può causare la variazione della TD associata ad una
data coppia di trasmettitori, e questo causerebbe un errore nella
determinazione del punto in cui il ricevente si trova. Per evitare problemi di
questo tipo sono presenti sul globo delle stazioni SAM (System Area Monitor).
Esse sono costituite da ricevitori Loran che controllano la TD di una
determinata coppia Master-Slave; se la TD in questione non è costante queste
stazioni di controllo o provvedono a correggerla, oppure avvisano gli utenti
del non perfetto funzionamento del sistema.
Gli utenti del sistema Loran-C, per
determinare le varie TD che permettono loro di conoscere la propria posizione,
utilizzano degli orologi atomici simili a quelli utilizzati sulle stazioni
trasmittenti. In questo modo è possibile ottenere informazioni con un buon
margine d'errore. Se infatti consideriamo orologi che registrano la TD con una
precisione di 5![]() 10-7 s otteniamo una precisione nella
determinazione della distanza di (considerando che i segnali viaggiano alla
velocità della luce):
10-7 s otteniamo una precisione nella
determinazione della distanza di (considerando che i segnali viaggiano alla
velocità della luce):
![]()
Dopo questa breve descrizione del funzionamento del sistema di radionavigazione Loran-C, dobbiamo vedere in che cosa questo sistema dipenda dalla teoria della relatività.
Consideriamo una nave che si trova a metà strada fra due trasmettitori Loran (una coppia Master-Slave) e cerchiamo di determinare la differenza di tempo (TD) tra i radiosegnali che arrivano alla nave (Figura 1.2).
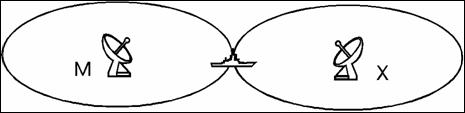 Fig. 1.2
Fig. 1.2
Secondo la teoria della relatività la velocità dei due segnali è identica visto che è quella della luce (che è una costante); perciò essendo uguale anche la distanza della nave dai due trasmettitori possiamo concludere che i due radiosegnali impiegano lo stesso tempo ad arrivare alla nave e quindi TD è uguale a zero.
Consideriamo ora il problema utilizzando la
fisica classica (ammettendo quindi l'esistenza dell'etere). In questo caso la
velocità v1 con cui il segnale arriva dal trasmettitore di sinistra
alla nave è c![]() v, mentre la velocità v2 del secondo radiosegnale
è c
v, mentre la velocità v2 del secondo radiosegnale
è c![]() v considerando la velocità orbitale del Sole nella galassia
pari a v. Perciò il tempo t1 che impiega il primo segnale ad
arrivare alla nave è:
v considerando la velocità orbitale del Sole nella galassia
pari a v. Perciò il tempo t1 che impiega il primo segnale ad
arrivare alla nave è:
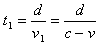
Il tempo t2 che serve al secondo segnale per arrivare alla nave è invece:
![]()
La differenza di tempo tra i due segnali è quindi:
![]()
Vediamo come in questo caso la differenza di
tempo non è affatto zero; questo comporta un errore ![]() nella determinazione
della posizione pari a:
nella determinazione
della posizione pari a:
![]()
Se prendiamo d = 1000 km e v = 200 km/s
avremo: ![]()
Questo errore renderebbe quindi inutilizzabile il sistema Loran-C perché sposterebbe le rotte delle navi di distanze maggiori del chilometro con gravi pericoli per le navi stesse.
Il GPS (Global Positioning System) è un sistema di navigazione globale che, utilizzando i dati che provengono da diversi satelliti, è in grado di informare gli utenti riguardo alla loro posizione o alla loro velocità.
Il sistema può essere diviso in tre segmenti:
Segmento spaziale;
Segmento di controllo;
Segmento di utilizzazione.
Questo primo segmento comprende 24 satelliti (21 di servizio e 3 di riserva) che si muovono su 6 orbite circolari inclinate di 50° rispetto al piano equatoriale. Ogni satellite ha un periodo di rivoluzione pari a 12 h e quindi si trova ad un'altezza dalla superficie terrestre di circa 20200 km.
I satelliti sono posizionati sulle varie orbite in modo tale che almeno quattro di essi siano visibili da ogni punto del globo terrestre.
Il secondo segmento del GPS è composto da sei stazioni di controllo (Figura 3.1) che hanno la funzione di calcolare ed inviare ai satelliti i dati relativi sia agli orologi atomici che sono presenti sui satelliti, sia alle orbite dei satelliti stessi. Ricevuti questi dati, ogni satellite li utilizza per inviare ai ricevitori il proprio Segnale di Navigazione cioè quel segnale che contiene tutte le informazioni riguardo al satellite stesso e che sono indispensabili al ricevitore GPS per calcolare la propria posizione rispetto al satellite trasmittente.
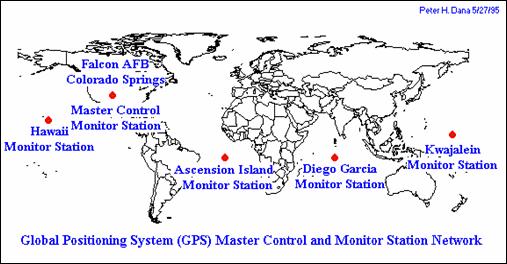 Fig.3.1
Fig.3.1
Il terzo segmento è ovviamente formato dai ricevitori GPS sparsi sulla Terra. Il compito di questi ricevitori è quello di contattare i satelliti e di calcolare la propria posizione grazie ai dati da essi ricevuti.
Vi sono differenti tipi di ricevitori ognuno dei quali ha un proprio grado di precisione ed una sua velocità nell'acquisizione del segnale.
Il principio su cui si basa il funzionamento del GPS è piuttosto semplice.
Prendiamo il caso che si voglia conoscere in che punto della Terra ci troviamo. Se sappiamo che siamo ad una distanza di 10000 km da un dato satellite A ciò significa che la nostra posizione si trova sulla sfera che ha come centro A e come raggio 10000 km (Figura 3.2).
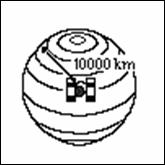 Fig.3.2
Fig.3.2 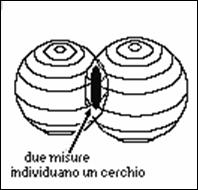 Fig.3.3
Fig.3.3
Se poi conosciamo la nostra distanza (ad esempio 11000 km) da un altro satellite (B) possiamo sapere che ci troviamo sull'intersezione fra le due sfere, una di centro A e raggio 10000 km e l'altra di centro B e raggio 11000 km; questa intersezione non è altro che un cerchio (Figura 3.3).
|
|
Se infine misuriamo la nostra distanza da un terzo satellite C (trovando che essa è pari a 9000 km) noi saremo in grado di determinare la nostra posizione poiché esistono solo due punti nello spazio in cui le tre sfere determinate dai tre satelliti si possono incontrare (Figura 3.4).
L'ultimo problema che rimane è decidere quale dei due punti rimasti è quello corrispondente alla nostra posizione. Per fare ciò basta notare come solo uno di questi due punti si trovi sulla superficie terrestre (ed è quindi quello che interessa a noi), mentre l'altro è nello spazio.
Il sistema sopra illustrato vale solo in linea teorica, infatti perché sia possibile determinare la posizione dell'utente con questo metodo sono necessari tre misurazioni perfette cioè non affette da grossi errori, ma questo renderebbe necessario l'utilizzo, da parte dell'utente, di un orologio atomico (che è però molto costoso). Per risolvere questo problema è sufficiente fare un'altra misurazione da un quarto satellite. Un esempio chiarirà meglio questa situazione.
|
|
Prendiamo il caso in cui noi ci troviamo a 4 secondi da un satellite A e a 6 da un satellite B; in due dimensioni queste due informazioni sono sufficienti per determinare la nostra posizione (X) (Figura 3.5). Ma se noi utilizziamo un orologio che è in ritardo di un secondo, la distanza da A diverrà 5 secondi e quella da B 7 secondi; questi due nuovi cerchi s'intersecheranno in un punto sbagliato (XX) (Figura 3.6).
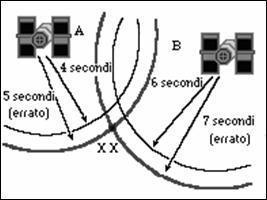 Fig.3.6
Fig.3.6
|
|
|
|
Ora aggiungiamo una nuova misurazione ai nostri dati (distanza di 8 secondi dal satellite C). Utilizzando un orologio che non commette errori ritroveremo ancora il punto (X) (Figura 3.7); se invece utilizziamo l'orologio che sbaglia di un secondo ci troveremo in una situazione particolare: i tre cerchi non s'incontreranno mai in un unico punto (Figura 3.8). In questa situazione il ricevitore GPS comprende che c'è qualcosa che non va; perciò comincia ad aggiungere (o a togliere) uno stesso tempo a tutte le misurazioni; continua a fare ciò finché non trova una situazione per cui i tre cerchi s'intersechino in un unico punto (X).
Questo esempio chiarisce come sia possibile, utilizzando quattro misurazioni, eliminare gli errori dovuti agli orologi presenti nel nostro ricevitore. Inoltre in questo modo la precisione del sistema nel determinare la posizione dell'utente diventa molto alta.
Finora abbiamo parlato di fare delle misurazione della distanza da diversi satelliti; ora vedremo come è possibile per un ricevitore GPS calcolare questa distanza.
Innanzi tutto è necessario conoscere la velocità con cui il segnale arriva dal satellite; questa velocità è la velocità della luce (300000 km/s). Il secondo problema deriva dal fatto che, per determinare il tempo necessario al segnale per arrivare al ricevitore, è indispensabile sapere quando questo è partito dal satellite. Per risolvere questo secondo problema si utilizza il seguente metodo: si sincronizzano il satellite e il ricevitore in modo che generino lo stesso codice nello stesso momento; quando riceviamo il segnale non dobbiamo far altro che controllare da quanto tempo il nostro ricevitore ha generato lo stesso codice; questa differenza di tempo è quanto ha impiegato il segnale per raggiungerci.
A questo punto moltiplichiamo il tempo trovato per la velocità della luce ed abbiamo la distanza cercata.
Oltre agli errori dovuti agli orologi vi sono altri fattori che determinano l'esattezza delle misurazioni.
Uno di questi fattori è ad esempio la ionosfera (uno strato di particelle cariche che va da 100 a 300 km di altezza); infatti le particelle di cui essa è composta abbassano la velocità del segnale rendendo imprecisa la misurazione della distanza dal satellite.
Un altro fattore che fa variare la precisione delle misurazioni è la posizione dei satelliti; l'errore in questo caso è minimo quando un satellite è allo zenit e gli altri tre sono equispaziati intorno al ricevitore.
Dobbiamo ora verificare, come abbiamo fatto per il Loran-C, come il sistema GPS dipenda dalla teoria della relatività. Per fare ciò ci poniamo in una situazione più semplice rispetto alla realtà: prendiamo due satelliti GPS (A e B) in modo tale che la retta che li congiunge sia tangente alla superficie terrestre; chiamiamo P il punto di tangenza tra la retta e la superficie. Per semplificare la situazione considereremo i due satelliti come geostazionari (cioè con periodo di rivoluzione attorno alla terra pari a 24h). Mettiamo che un utente, che si trova nel punto P, voglia conoscere la propria posizione utilizzando il GPS e valutiamo l'errore che si commetterebbe risolvendo il problema utilizzando la fisica classica invece che la teoria della relatività (Figura 3.9).
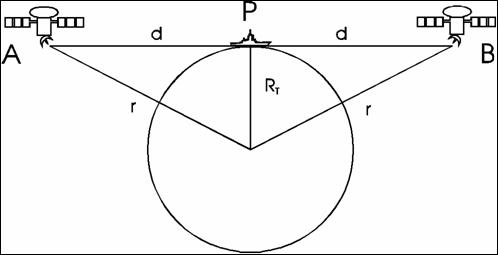 Fig. 3.9
Fig. 3.9
Innanzitutto dobbiamo determinare la distanza che separa ciascun satellite dal punto P (la distanza è la stessa per entrambi i satelliti perché è uguale il loro periodo di rivoluzione attorno alla Terra). Per fare ciò necessitiamo della distanza dei satelliti dal centro della Terra, che può essere determinata con la terza legge di Keplero per i satelliti; perciò abbiamo:
![]()
In cui T è il periodo di rivoluzione del
satellite attorno alla Terra (86400 s), G è la costante di gravitazione
universale (6,672![]() 10-11 Nm2/kg2), MT
è la massa della Terra (5,976
10-11 Nm2/kg2), MT
è la massa della Terra (5,976![]() 1024 kg) e r è la distanza del satellite dal
centro della Terra (che è ciò che vogliamo trovare); perciò si ricava che:
1024 kg) e r è la distanza del satellite dal
centro della Terra (che è ciò che vogliamo trovare); perciò si ricava che:
![]()
A questo punto possiamo ricavare la distanza (d) dei satelliti dal punto P usando il teorema di Pitagora (RT è il raggio terrestre pari a 6370 km):
![]()
Se studiamo questo esempio utilizzando la teoria della relatività vediamo come la differenza di tempo con cui i due segnali raggiungono il punto P è zero (entrambi i satelliti si trovano alla distanza d dal punto P ed i rispettivi segnali viaggiano alla medesima velocità).
Se invece utilizziamo la fisica classica la
velocità con cui i segnali viaggiano verso P sarà diversa satellite per
satellite. Questa velocità sarà influenzata ad esempio dalla velocità con cui
la Terra si muove attorno al Sole; vediamo in che misura questo cambiamento
nella velocità dei segnali varierebbe la precisione del sistema GPS.
Innanzitutto dobbiamo calcolare la lunghezza dell'orbita terrestre (OT);
per fare ciò ci serviamo della distanza media della Terra dal Sole (R = 1,496![]() 1011 m). Avremo perciò:
1011 m). Avremo perciò:
![]()
Poiché il periodo di rivoluzione T della
Terra è un anno (pari a 3,154![]() 107s) la velocità media di rivoluzione cercata
sarà:
107s) la velocità media di rivoluzione cercata
sarà:
![]()
Perciò le velocità con cui i due segnali raggiungono il punto P saranno rispettivamente
![]() per il satellite 1, e
per il satellite 1, e
![]() per il satellite 2.
per il satellite 2.
Da questo si ricava che i tempi che impiegheranno i due segnali a raggiungere il punto P saranno:
![]() e
e ![]()
Per una differenza di tempo pari a: ![]()
Questo comporterebbe un errore ![]() nella determinazione
di P che sarebbe uguale a:
nella determinazione
di P che sarebbe uguale a: ![]()
Tutto quello detto finora ha fatto vedere come la relatività stia entrando nella tecnologia e quindi nella vita di tutti i giorni; in futuro questo avverrà sempre più spesso visto che il numero di utenti che utilizzano i due sistemi che abbiamo analizzato stanno aumentando moltissimo. Questo è vero soprattutto per il GPS che viene ad esempio sfruttato per i sistemi di navigazione delle auto oppure viene utilizzato in gran parte delle spedizioni scientifiche che si svolgono in luoghi dove è necessario conoscere con precisione la propria posizione (ad esempio spedizioni ai Poli).
Possiamo quindi concludere che in un futuro non troppo lontano la nostra vita dipenderà in modo sempre maggiore da una teoria che meno di un secolo fa appariva come irreale ed assurda.
1. Premessa.......... ..... ...... .......... ..... ...... ........................
2. Introduzione.......... ..... ...... .......... ..... ...... ...............
3. Loran-C........... ..... ...... .......... ..... ...... ...........................
3.1 Generalità e funzionamento........... ..... ...... .........................
3.2 Identificazione del segnale........... ..... ...... ...........................
3.3 Sincronizzazione........... ..... ...... .......... ..... ...... ............
3.4 Precisione........... ..... ...... .......... ..... ...... ......................
3.5 Relatività e Loran-C........... ..... ...... .......... ..... ...... .....
4. GPS........... ..... ...... .......... ..... ...... .......... ..... ...... .....
4.1 Generalità........... ..... ...... .......... ..... ...... .....................
4.1.1 Segmento spaziale........... ..... ...... .......... ..... ...... ......
4.1.2 Segmento di controllo........... ..... ...... .......... ..... ...... .
4.1.3 Segmento di utilizzazione........... ..... ...... ...........................
4.2 Funzionamento........... ..... ...... .......... ..... ...... ............
4.3 Misurazione della distanza da un satellite........... ..... ...... .
4.4 Altri tipi di errore........... ..... ...... .......... ..... ...... ........
4.5 Relatività e GPS........... ..... ...... .......... ..... ...... ..........
5. Conclusione.......... ..... ...... .......... ..... ...... ...............
6. Soommario.......... ..... ...... .......... ..... ...... ..................
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025