§& 949h72j nbsp;    MOLTIPLICAZIONE

x1+iy1*x2+iy2=(x1*x2)+(y1*y2*(-1)) + i ((y1*x2)+(x1*y2))

§& 949h72j nbsp;    DIVISIONE

x1+iy1 / x2+iy2=((x1+iy1) * (x2+iy2)) / ((y2+iy2) * (y2-iy2)

§& 949h72j nbsp;    MODULO

Mod(x1+iy1)=sqr((x1^2+(-y^2))

Innanzitutto ho svolto il programma in pascal:

DATI INPUT-OUTPUT

Input:

o& 949h72j nbsp;  Parte reale e immaginaria del primo numero complesso

o& 949h72j nbsp;  Parte reale e immaginaria del secondo numero complesso

o& 949h72j nbsp;  Operazione da svolgere

Output

A seconda della richiesta (somma,differenza,moltiplicazione,divisione,modulo)

Program numericomplessi;

Type complex=record

Rea:integer;

Imm:=integer;

Var z1,z2:complex ;

Var risposta :=string ;

Begin

Function sommanum:complex;

begin

sommanum.Rea:=(z1.Rea+z2.Rea)

sommanum.Imm:=(z1.Imm+z2.Imm)

writeln('la somma è ',sommanum.Rea,'+',sommanum.Imm,'i')

end;

Function sottrainum:complex;

begin

sottrainum.Rea:=(z1.Rea-z2.Rea)

sottrainum.Imm:=(z1.Imm-z2.Imm)

writeln('la somma è ',sottrainum.Rea,'+',sottrainum.Imm,'i')

end;

Function moltinum:complex;

begin

moltinum.Rea:=((z1.Rea*z2.Rea)+(z1.Imm*z2.Imm*(-1)))

moltinum.Imm:=(z1.Imm*z2.Rea)+(z1.Rea*z2.Imm)

writeln('il prodotto è ',moltinum.Rea,'+',moltinum.Imm,'i')

end;

Function divinum:complex;

begin

divinum.Rea:=((z1.Rea*z2.Rea+(-(z1.Imm*z2.Imm*(-1)))/(z2.Imm*z2.Imm+z2.Rea*z2.Rea)

divinum.Imm:=((z1.Imm*z2.Rea)+(z1.Rea*z2.Imm*(-1))/(z2.Imm*z2.Imm+z2.Rea*z2.Rea)

writeln('il quoziente è ',divinum.Rea,'+',divinum.Imm,'i')

end;

function modulonum(mod1,mod2:integer):integer;

begin

mod1:=sqr(z1.Rea*z1.Rea-z1.Imm*z1.Imm);

mod2:=sqr(z2.Rea*z2.Rea-z2.Imm*z2.imm);

writeln(il modulo di z1 è ',mod1,' e il modulo di z2 è ''mod2);

end;

Writeln('dammi la parte reale e immaginaria del primo numero complesso');

readln(z1.Rea,z1.Imm);

Writeln('dammi la parte reale e immaginaria del secondo numero complesso');

readln(z2.Rea,z2.Imm);

writeln('che operazione vuoi fare?');

readln(risposta);

if risposta = somma then

sommanum

else if risposta =divisione then

divinum

else if risposta = moltiplicazione then

moltinum

else if risposta =sottrazione then

sottrainum

else if risposta=modulo then

modulonum

end.

FUNZIONI UTILIZZATE

1. Variabile di tipo astratto (complex)
2. Uso di function
3. Struttura iterativa if-then-else

STRUTTURA DEL PROGRAMMA

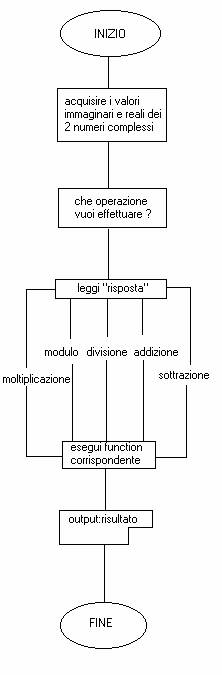
Ho poi applicato un'interfaccia grafica al precedente programma.Per farlo ho utilizzato il linguaggio Visual Basic 6.0

Private Sub Command1_Click() [1]

Dim a As Integer

Dim b As Integer

Dim c As Integer

Dim d As Integer

a = Text1

b = Text2

c = Text4

d = Text5

visibile

Text3 = a + c

Text6 = b + d

Label1.Caption = "+"

text

End Sub

Private Sub Command2_Click()    [2]

Dim a As Integer

Dim b As Integer

Dim c As Integer

Dim d As Integer

a = Text1

b = Text2

c = Text4

d = Text5

visibile

Text3 = a - c

Text6 = b - d

Label1.Caption = "-"

text

End Sub

Private Sub Command3_Click() [3]

Dim a As Integer

Dim b As Integer

Dim c As Integer

Dim d As Integer

a = Text1

b = Text2

c = Text4

d = Text5

visibile

Text3 = a * d + b * c

Text6 = b * d + (-a * c)

Label1.Caption = "*"

text

End Sub

Private Sub Command4_Click()  [4]

Dim a As Integer

Dim b As Integer

Dim c As Integer

Dim d As Integer

a = Text1

b = Text2

c = Text4

d = Text5

visibile

Text3 = ((a * d) + (b * c * (-1))) / (d * d + c * c)

Text6 = (b * d + (-(a * c * (-1)))) / (d * d + c * c)

Label1.Caption = "/"

text

End Sub

Private Sub Frame1_DragDrop(Source As Control, X As Single, Y As Single)

End Sub

Public Function text() [6]

Response = MsgBox("altro calcolo?", vbYesNo)

If Response = vbYes Then

Text1.text = ""

Text2.text = ""

Text3.text = ""

Text4.text = ""

Text5.text = ""

Text6.text = ""

Label1.Caption = ""

Label2.Caption = ""

visibile_no

Else

End

End If

End Function

Function visibile() [7]

Label2.Visible = True

Text3.Visible = True

Text6.Visible = True

Label7.Visible = True

Label8.Visible = True

End Function

Function visibile_no()

Label2.Visible = False

Text3.Visible = False

Text6.Visible = False

Label7.Visible = False

Label8.Visible = False

Text7.Visible = False

Text8.Visible = False

Picture1.Visible = False

Picture2.Visible = False

End Function

Private Sub Command5_Click()    [8]

Dim a As Integer

Dim b As Integer

Dim c As Integer

Dim d As Integer

a = Text1

b = Text2

c = Text4

d = Text5

Picture1.Visible = True

Picture2.Visible = True

Text7.Visible = True

Text8.Visible = True

Text7 = Sqr((a * a) + (b * (-b)))

Text8 = Sqr((c * c) + (d * (-d)))

text

End Sub

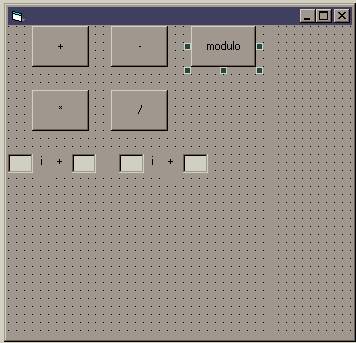
Questa è la form principale.Come si nota sono presenti 5 bottoni,ognuno corrispondente ad una funzione già definita. I 4 edit in basso rappresentano invece la parte reale e immaginaria dei 2 nuemri complessi.

TRACING

Proviamo a dividere 2 numeri complessi per poi verificare che il programma funzioni correttamente.

Z1: 6 + 8i

Z2: 4 - 3i

(6 + 8i) * (4 + 3i) 24 + 18i + 32i + 24i²

(6+8i) / (4-3i) =   ----- ----- ----------- = ----- ----- ---------------

(4 - 3i) * (4 + 3i) 16 - 9i²

sappiamo che in campo immaginario i²=-1; andando a sostituire:

24 + 50i -24 0 50i

----- ----- -------- = ------ + ------ = 0 + 2i

16 + 9 25 25

Andiamo ora a confrontare il risultato ottenuto con l'esecuzione del programma

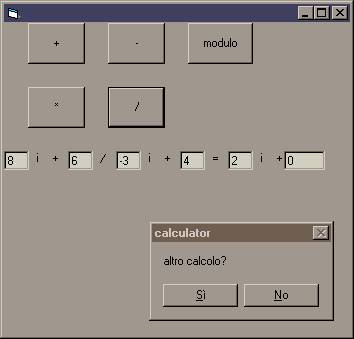
il programma è verificato.

ANALISI DEL PROGRAMMA

Oggetti usati

Button 1

ü& 949h72j nbsp; Button1.visible=true

ü& 949h72j nbsp; Button1.caption='+'

Questo bottone rappresenta il comando +

Button 2

ü& 949h72j nbsp; Button2.visible=true

ü& 949h72j nbsp; Button2.caption='-'

Questo bottone rappresenta il comando -

Button 3

ü& 949h72j nbsp; Button3.visibile=true

ü& 949h72j nbsp; Button3.caption='*'

Questo bottone rappresenta il comando *

Button 4

ü& 949h72j nbsp; Button4.visible=true

ü& 949h72j nbsp; Button4.caption='/'

Questo bottone rappresenta il comando /

Button 5

ü& 949h72j nbsp; Button5.visible=true

ü& 949h72j nbsp; Button5.caption='modulo'

Questo bottone rappresenta il commando modulo

Text1,text2,text4,text5

ü& 949h72j nbsp; .visible=true

ü& 949h72j nbsp; .caption=blank

Questi 4 edit servono per immettere I 2 numeri complessi nella loro parte reale ed immaginaria

Text5,text6

ü& 949h72j nbsp; .visible=false

ü& 949h72j nbsp; .caption=blank

Questi 2 edit sono la parte reale ed immaginaria del risultato.La visibilità si attiva non appena viene premuto qualsiasi bottone.

Text7,text8

ü& 949h72j nbsp; .visible=false

ü& 949h72j nbsp; .caption= blank

Questi 2 edit sono i 2 risultati dei moduli dei 2 numeir complessi.la visibilità si attiva non appena viene premuto il bottone  "modulo " .

Picture1.picture2

ü& 949h72j nbsp; .visible=false

ü& 949h72j nbsp; .picture=freccia.jpg

Queste 2 frecce riconducono ai text 7 e text 8.La visibilità si attiva non appena vien premuto il bottone "modulo".

Msg box

Il msg box chiede se si vuole fare un altro calcolo:se si ricomincia altrimenti il programma si chiude automaticamente.

PROCEDURE E FUNCTION USATE

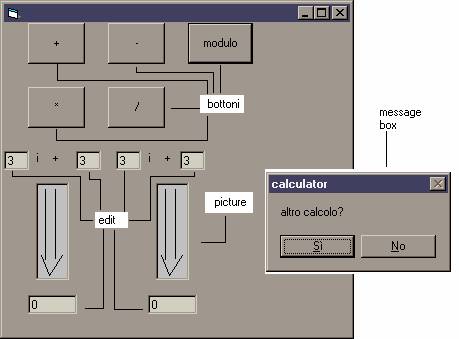
Procedura Button 1,2,3,4,5

Il procedimento dei 5 bottoni è pressoché identico;

• Vengono inizializzate le 4 variabli a,b,c,d che corrispondono alle parti reali ed immaginarie dei 2 numeri complessi come variabili di tipo integer
• Ad ogni edit è assegnata una variabile
• Parte la procedura visibile
• Viene svolta l'operazione e fornito il risultato
• Parte la procedura text

Function text

Finito il calcolo,viene chiesto attraverso una msg box se eseguire un altro calcolo.A risposta affermativa vengono azzerati tutti gli edit e parte la procedura visibile_no

Function visible e visible_no

Attivano rispettivamente la visiblità in true e false delle varie edit e label per un fatto puramente estetico.

DIFFICOLTA' RISCONTRATE

Il lavoro è stato abbastanza lungo ma non ho avuto particolari problemi.Per scrivere correttamente le formule di divisione e moltiplicazione ho devoto effettuare diversi tracing prima di ottenere l'algoritmo corretto