|
|
| |
LA RIDUZIONE A SOTTOPROBLEMI.
La linea generale nella risoluzione per scomposizione a sottoproblemi consiste nel "ragionare all'indietro" partendo dal problema da risolvere e individuandone sottoproblemi e sotto sotto-problemi finché il problema originario non si è ridotto ad un insieme di problemi primitivi banali .
Per illustrare come un problema potrebbe essere risolto con il metodo della riduzione a sotto problemi
consideriamo un rompicapo: si tratta di una versione del gioco della torre di Hanoi, costituito da tre pioli
(1, 2 e 3) e tre dischi di diverso diametro (A , B, C).Questi sono forati nel centro in modo da poter essere
infilati sui pioli. All' inizio i dischi si trovano tutti sul piolo 1, con il più largo (C) sotto agli altri e
il più piccolo (A) in cima. Si desidera trasferire i dischi al piolo 3 muovendo 656b14g un disco per volta, purché sia
prelevato dalla cima di una pila e non venga posto su di un disco più piccolo.
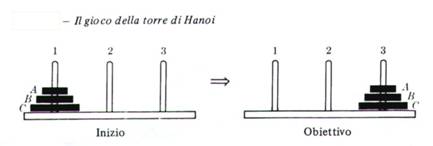
Riduciamo il problema originale ai tre problemi seguenti:
1 ) trasferire A e B al piolo 2 (gioco a due dischi):
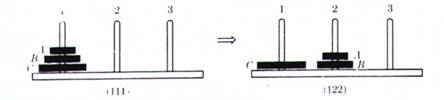
2 ) trasferire C al piolo 3 (gioco a un disco):
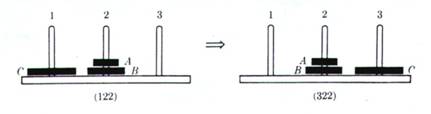
3 ) trasferire A e B al piolo 3 (gioco a due dischi):
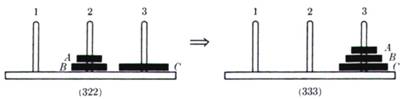
In effetti il problema 2 si può considerare primitivo giacché la soluzione richiede una sola mossa.
Ripetendo il ragionamento si possono ridurre anche 1e 3 a problemi primitivi, come è mostrato
schematicamente in figura
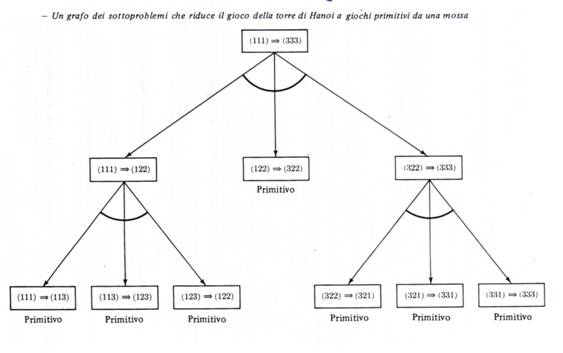
il metodo della riduzione a sotto problemi impiega operatori che trasformano una descrizione di problema
in una descrizione di sottoproblemi . Le descrizioni di problema possono presentare svariate forme, si usano
liste, alberi,vettori,tabelle.
Nel gioco della torre di Hanoi i sottoproblemi si possono descrivere con una lista di due liste. Così la
descrizione [(113),(333)], significa: " mutare la disposizione(113) nella posizione(333)".
E' conveniente rappresentare la riduzione di un problema ad insiemi alternativi di problemi successori
mediante una struttura simile ad un grafo.Si supponga che il problema A si possa risolvere risolvendo
i problemi B e C, o D e E ,o F; questa situazione si rappresenta con la struttura seguente
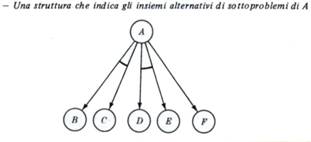
I problemi B e C costituiscono un insieme di problemi successori ,i problemi D e E un altro, e il problema F un terzo. I nodi corrispondenti ad un dato insieme sono indicati da un segno speciale che collega i loro archi entranti.
Di solito si introducono nella struttura nodi supplementari cosicché ogni insieme che contiene più di un
problema successore si trova raggruppato sotto il suo nodo padre.
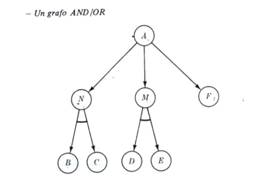
Uno dei nodi di tale grafo , detto nodo di partenza , corrisponde alla descrizione del problema originale.
I nodi corrispondenti a descrizioni di problemi primitivi si dicono terminali .
.La definizione di nodo risolto in un grafo AND/OR si può dare ricorsivamente come segue:
a) i nodi terminali sono risolti
b) se un nodo non terminale ha successori OR , esso è risolto se e solo se almeno uno dei sui successori è risolto;
c) se un nodo non terminale ha successori AND, esso è risolto se e solo se tutti i suoi successori sono risolti.
Si definisce grafo risolutivo il sottografo di nodi risolti che dimostra che il nodo di partenza è risolto
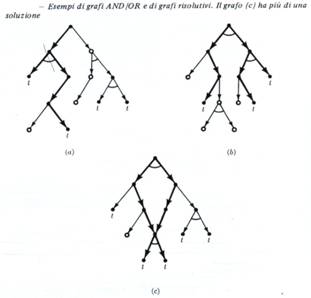
Il processo di risoluzione di un problema corrisponde quindi alla ricerca di un sottografo AND/OR che permetta di etichettare come risolto il nodo che rappresenta il problema iniziale ( al solito il grafo viene costruito durante il processo di ricerca ).
Il metodo di riduzione a sottoproblemi si può anche usare per trovare strategie in certi tipi di giochi detti a due
persone ed a informazione completa;sono giocati da due giocatori che muovono a turno e l'esito del gioco può essere vittoria di un giocatore o parità.
es : scacchi , dama , tris ,etc.
Il metodo di riduzione trova una strategia vincente attraverso la dimostrazione che il gioco può essere vinto.
Dopo aver descritto il problema e definito gli operatori di riduzione a sottoproblemi si può generare un
grafo AND/OR per risolvere il problema iniziale o per dimostrare la sua insolubilità.
La generazione di questo grafo richiede un processo di ricerca che termina con successo quando si trova un grafo risolutivo.
I processi di ricerca in seguito esaminati comportano i seguenti passi:
La struttura dei nodi e dei puntatori generati dal processo di ricerca forma un grafo AND/OR che è un sottografo dell'intero grafo definito implicitamente .I metodi di ricerca per i grafi AND/OR si differenziano soprattutto per il modo di ordinare i nodi da espandere.
I metodi in ampiezza espandono i nodi nell'ordine in cui vengono generati,
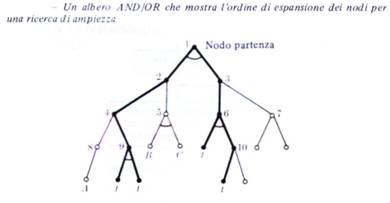
e i metodi in profondità espandono prima l'ultimo nodo generato.
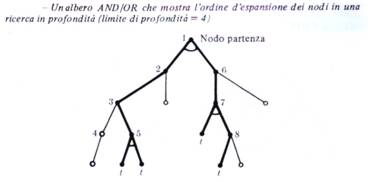
I metodi di maggiore interesse sono quelli di ricerca ordinata che fanno uso di valutazione euristica per ordinare l'espansione dei nodi.
Ogni qualvolta una riduzione a sottoproblemi produce un problema successore equivalente ad uno già prodotto dal processo di ricerca, la struttura che si ottiene si può rappresentare con un grafo AND/OR che ammette nodi con più di un genitore piuttosto che con un albero.
Se siamo in grado di riconoscere le equivalenze nella riduzione a sottoproblemi riusciamo in generale a ridurre lo sforzo di ricerca perché problemi identici vengono risolti una sola volta .Inoltre, la struttura di grafo generico rivela i cicli superflui (ragionamenti circolari) che si possono verificare ma che non sarebbero scoperti se descrizioni di problemi effettivamente identiche fossero riguardate come differenti nella rappresentazione ad albero.
I metodi di ricerca si semplificano notevolmente nel caso degli alberi piuttosto che nel caso dei grafi generici
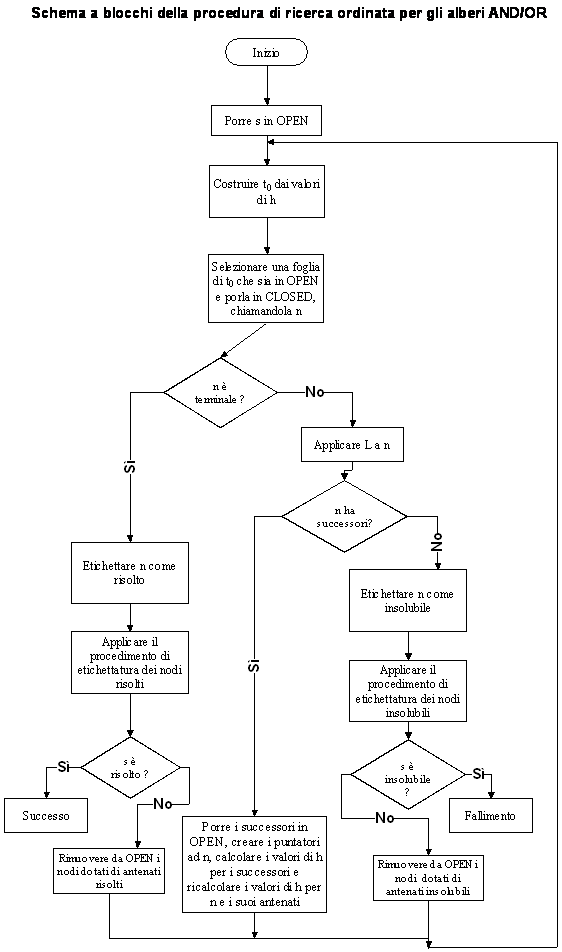
Di seguito vengono schematizzate le procedure di ricerca in ampiezza e in profondità nel caso di alberi AND/OR
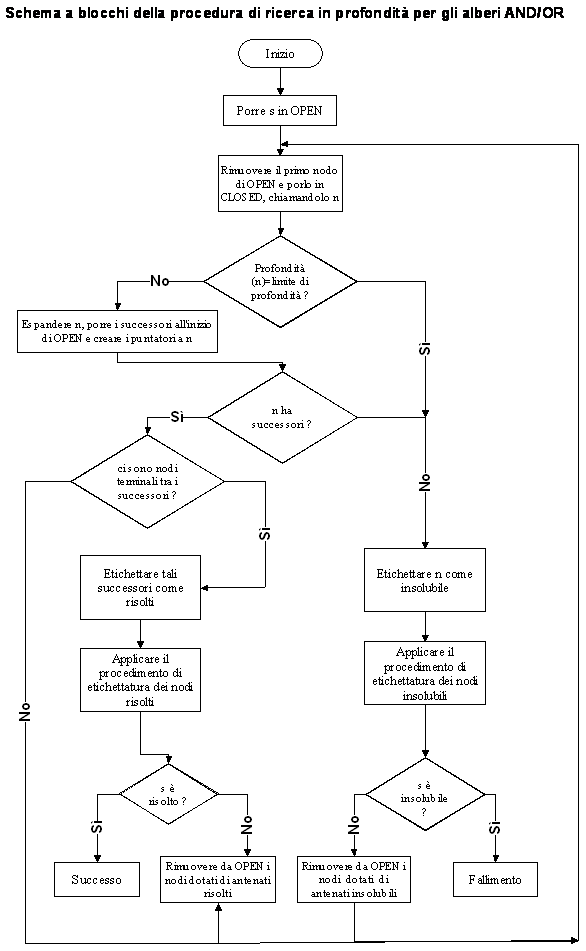
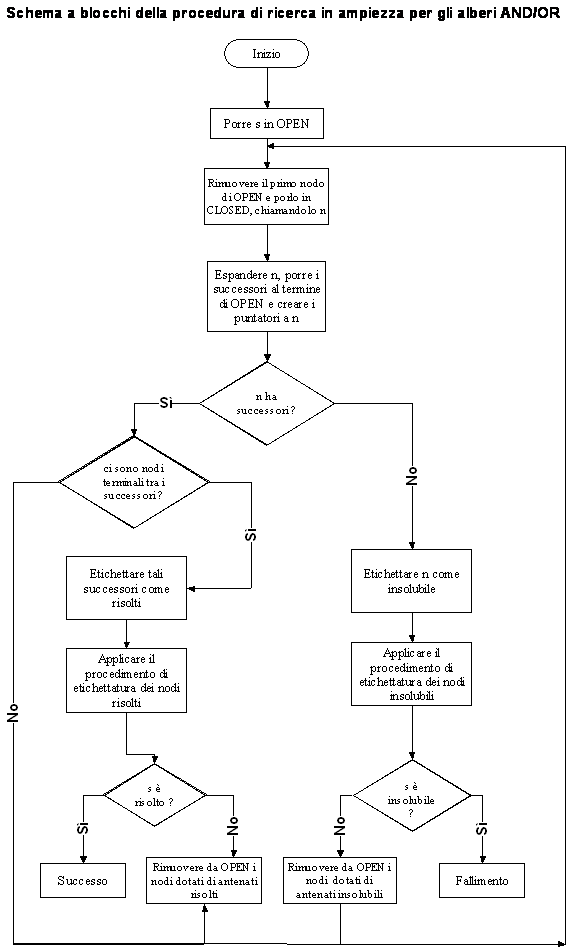
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025