Le geometrie non euclidee

Dal V postulato Euclide, nella proposizione 30, ricava il seguente teorema, che è equivalente al postulato ed è stato usato storicamente per i tentativi di dimostrazione dello stesso: Per un punto esterno ad una retta passa una e una sola retta parallela a quella data.

Le prime critiche

I primi critici di Euclide (e cosí fino al 1800) cercarono di dimostrare il V postulato in base ai primi, ritenendolo un punto logicamente debole della costruzione euclidea, cosí Proclo (410-435 d.C.) che nei sui tentativi giunse soltanto a sostituirlo con vari postulati equivalenti, e nel Rinascimento Wallis (1616-1703) dedusse dall'esistenza di figure simili il V postulato: questo ha una grande importanza, nelle geometrie non euclidee non esistono figure simili, perché variando le lunghezze variano anche gli angoli (questa variazione prende il nome di eccesso angolare).

Girolamo Saccheri

Un grande passo avanti fu fatto dal gesuita italiano Girolamo Saccheri (1667-1773) che cercò di dimostrare il V postulato a contrariis: partendo dalla negazione del postulato delle parallele si aspettava di trovare qualche contraddizione e quindi la negazione dell'ipotesi.

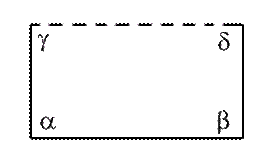
Individua due ipotesi alternative al V postulato:

1. che due perpendicolari ad una retta formino due angoli ottusi (gamma e delta) con una parallela alla retta data
2. che formino invece angoli acuti

Ne dà poi due confutazioni errate, ma rimane la grandissima importanza d'essere stato il primo a tentare la via delle geometrie non euclidee.

La geometria iperbolica

Solo nel 1800 Gauss, Lobacevskij e Bolyai, indipendentemente l'uno dagli altri, dettero una sistemazione rigorosa dell'ipotesi degli angoli acuti: la geometria iperbolica.
Secondo questo tipo di geometria una retta ammette piú d'una parallela passante per un punto esterno alla retta stessa. Per comprendere questo tipo di geometria si è fatto inizialmente ricorso ad una ridefinizione delle primitive geometriche: se si definisce piano l'area interna ad un'ellisse e retta una qualsiasi corda di quest'ellisse si può intuire facilmente l'esistenza di infinite parallele passanti per un punto.

L'opera di Riemann

Il matematico tedesco Riemann rivoluzionò il concetto di geometria. Per Riemann geometria è lo studio di insiemi di ennuple ordinate che vengono raggruppati secondo certe regole; non è quindi vincolato ad uno spazio fisico, come pretendeva la geometria euclidea, definita come a priori da Kant nella Critica della ragion pura.

Oltre a questo elaborò la geometria delle superfici a curvatura positiva che fu poi adottata da Einstein per descrivere piú semplicemente lo spazio-tempo: secondo la teoria generale della relatività non esiste una forza di gravità, ma è la massa che incurva lo spazio-tempo, mentre i corpi, che a noi sembrano deviare, seguono la linea piú breve nello spazio-tempo curvo: una geodetica. Se immaginiamo l'universo come una distribuzione omogenea di materia in moto reciproco relativamente lento, possiamo dedurre che la curvatura dello spazio-tempo sia costante in ogni suo punto e che quindi, esso deve assumere la forma di un'ipersfera (sfera quadridimensionale), come in un piano una linea a curvatura costante positiva dà una circonferenza ed una superficie a curvatura costante positiva dà una sfera.

Da Riemann in poi non si è piú considerata la geometria come descrizione della realtà, ma come semplice interpretazione: non si tratta di scegliere la geometria "vera", ma quella che meglio descrive la realtà. Einstein non ha stabilito che la geometria euclidea non sia "vera", ma solo che adottando quella sferica la teoria della relatività risulta semplificata: la geometria ora è realmente fisica, è diventata cioè un modello interpretativo della natura.