OSCILLATORE ARMONICO - AUTOSTATI DELL'ENERGIA

(2)

Il vantaggio della evoluzione diagonale è quello di avere una singola equazione di evoluzione data dalla seconda delle due e di poter quindi esprimere a in termini del suo valore iniziale.

La parte reale e la parte immaginaria di a sono legate ai gradi di libertà posizione e quantità di moto. (Il termine "diagonale" si riferisce ad una notazione matriciale che riassume le due equazioni (1) in una singola equazione di evoluzione per un vettore di componenti x e p. Al secondo membro di t 858d33i ale equazione figura una matrice non diagonale. La diagonalizzazione di tale equazione porta a definire un nuovo vettore le cui componenti sono la parte reale e la parte immaginaria di a .)

Vogliamo determinare gli autostati dell'energia dell'operatore hamiltoniano corrispondente all'oscillatore armonico unidimensionale.

(3)

Nella (3) l'energia H è espressa come somma degli operatori corrispondenti all'energia cinetica e alla energia potenziale dell'O.A. unidimensionale. L'analogo del procedimento di diagonalizzazione porta ora a definire due operatori detti per motivi che saranno chiari nel seguito, operatori di abbassamento ed innalzamento.

(4)

Le regole di commutazione tra posizione e quantità di moto portano al seguente risultato per il commutatore degli operatori di innalzamento e abbassamento.

(5)

Notiamo come la lunghezza l , parametro arbitrario nella (4) si può scegliere così da fissare il commutatore tra gli operatori di innalzamento e abbassamento ad un valore unitario.

Tale scelta porterà ad una serie di conseguenze di significato fisico rilevante. In termini dei suddetti operatori l'hamiltoniana (3) prende una forma diagonale.

(6)

Come conseguenza della (5) otteniamo i commutatori tra l'hamiltoniana e gli operatori di abbassamento e innalzamento.

(7)

Le proprietà algebriche date dalla (7) permettono di costruire a partire da un dato autostato dell'energia, infiniti altri autostati con energia che si incrementa dall'uno al successivo di quantità pari ad un quanto se si sale lungo una scala ideale di cui ogni elemento è in corrispondenza con un autostato o si diminuisce della stessa quantità se si scende lungo la stessa scala. Questo risultato si stabilisce facilmente. Definiamo preliminarmente un autostato di H corrispondente all'autovalore E . A questo autostato associamo due stati che si ottengono applicando rispettivamente l'operatore di innalzamento e di abbassamento. Vogliamo dimostrare che tali stati sono anch'essi autostati e trovare gli autovalori corrispondenti.

(8)

(9)

In conseguenza della (7) abbiamo

(10)

E' importante determinare se tale "scala" ammetta un livello minimo che corrisponderà al cosiddetto stato fondamentale. Fissato un valore dell'energia ed il corrispondente autovalore si potrrà sempre "scendere" fino a raggiungere un livello di energia Eo tale che un ulteriore abbassamento dia luogo ad una energia negativa. Ma un autostato con energia negativa non e' ammissibile infatti la media di H su tale autostato sarebbe negativa

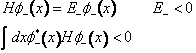(11)

Tale media si puo' esprimere come media dell'energia cinetica e dell'energia potenziale

(12)

Il secondo termine e' evidentemente positivo . Il secondo e' anche positivo come si evidenzia con una integrazione per parti.

(13)

L'unica soluzione possibile e' che

(14)

Con tale scelta, lo stato fondamentale è tale che l'operatore di abbassamento ci porta allo stato vuoto o, in altri termini, lo stato fondamentale è autostato di a con autovalore nullo.

E' possibile normalizzare gli autostati che si ottengono dallo stato fondamentale applicando successivamente l'operatore di innalzamento.

(15)

L'insieme degli autostati dell'hamiltoniana costruiti con un procedimento illustrato è un insieme completo ed ortonormale.

STATI COERENTI

Come esempio di stati "sovrapposizione" di autostati dell'energia di interesse fisico rilevante, vogliamo studiare i cosiddetti stati coerenti. Questi stati sono gli stati di un oscillatore armonico che più si avvicinano alle proprietà dell'oscillatore armonico classico. Li definiamo al tempo zero, come la seguente sovrapposizione di autostati dell'energia

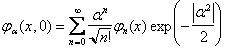(16)

Vogliamo verificare che tali stati sono autostati dell'operatore di abbassamento con autovalore a . Si noti che non essendo a un operatore hermitiano, il suo autovalore può benissimo essere un numero complesso.

(17)

La verifica procede come segue.

(18)

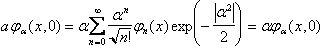(19)

La generalizzazione a tempi diversi da zero, si ottiene facilmente ricordando come si esprime lo stato del sistema al tempo t se lo si conosce al tempo t=0 come sovrapposizione di autostati dell'energia.

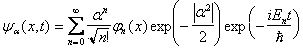(20)

Sostituendo nella (21) gli autovalori dell'energia dati dalla (15) si ottiene

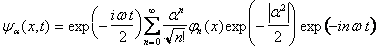(21)

INCERTEZZA SULLA POSIZIONE E SULLA QUANTITÀ DI MOTO NEGLI STATI STAZIONARI

Per caratterizzare gli stati stazionari e gli stati coerenti calcoliamo l'incertezza sulla posizione e sulla quantità di moto associate a questi stati. E' interessante vedere come queste grandezze si possano determinare utilizzando le proprietà degli operatori di abbassamento e di innalzamento prescindendo dalla conoscenza delle ampiezze di probabilità.

Per gli stati stazionari è facile dimostrare che il valor medio della posizione e della quantità di moto è nullo.

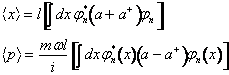(22)

Dalle (23) si ricava che ambedue i valori medi sono nulli in quanto gli operatori di abbassamento o di innalzamento trasformano uno stato in uno stato ortogonale. Peraltro il valor medio deve corrispondere ad una grandezza classica e classicamente lo statto stazionario è lo stato di quiete.

Per l'incertezza occorre considerare i momenti del secondo ordine

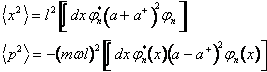(23)

Sviluppando il quadrato(attenzione a non commutare l'ordine  degli operatori) e sfruttando le proprietà (5) si ottiene

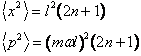(24)

Si noti come il prodotto di indeterminazione sia minimale per lo stato fondamentale (n=0) e cresca poi con il numero quantico

(25)

MOTO MEDIO ED INDETERMINAZIONE NEGLI STATI COERENTI

Anche in questo caso sia il valor medio che l'incertezza si possono calcolare utlizzando le proprietà degli operatori a, a⁺.

Per il valor medio abbiamo

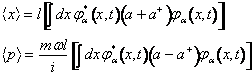(26)

Utilizzando la proprietà degli stati coerenti di essere autostati dell'operatore di abbassamento (20)

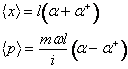(27)

Il valor medio rappresenta il moto classico dell'oscillatore. Ricordando l'espressione dell'autovalore dipendente dal tempo a(t) si ottiene infatti

(28)

Per l'incertezza conviene introburre degli operatori b, b⁺. Tali operatori hanno le stese regole di commutazione degli operatori di abbassamento ed innalzamento ed hanno media nulla sullo stato in cui si opera la media. Gli stati coerenti sono autostati di b con autovalore nullo. La differenza tra x o p ed il valor medio (scarto) si esprime immediatamente tramite gli operatori b, b⁺

(29)

L'incertezza quadratica si esprime in termini di questi operatori

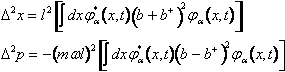(30)

Con passaggi del tutto analoghi ai precedenti si ottiene che

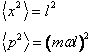(31)

Abbiamo raggiunto il notevole risultato che in uno stato coerente l'indeterminazione è pari a quella dello stato fondamentale dell'oscillatore armonico.

Gli stati coerenti diventano indistinguibili dagli stati di oscillazione classici se l'incertezza relativa è piccola, condizione facilmente realizzabile se l'ampiezza a à abbastanza elevata eccetto che agli istanti in cui si annullano rispettivamente la posizione o la quantità di moto.

(32)

FUNZIONI D'ONDA DI STATI STAZIONARI E COERENTI

Per ottenere le autofunzioni si possono utilizzare le relazioni che definiscono l,azione degli operatori di abbassamento ed innalzamento come equazioni differenziali la cui soluzione permette di determinare, insieme alla condizione di normalizzazione, le autofunzioni dell'oscillatore armonico.

(33)

La seconda delle (34) è una equazione differenziale che si può risolvere con il metodo della separazione delle variabili. La soluzione normalizata è

(34)

Si noti come la lunghezza l, introdotta inizialmente per rendere il commutatore di x e p unitario, e che abbiamo visto successivamente caratterizzare l'incertezza della posizione associata allo stato fondamentale, definisca ora completamente lo stato fondamentale.

Gli altri stati stazionari o stati eccitati si ottengono applicando successivamente l'operatore di innalzamento allo stato fondamentale.

(35)

Per gli stati coerenti conviene prima esprimere uno stato coerente in modo alternativo alla (22).

(36)

Si dimostra che la (36) è equivalente alla (22) utilizzando la seguente identità operatoriale

(37)

Tale identità è un caso particolare di una identità che permette di scrivere l'esponenziale di una somma di operatori come prodotto degli esponenziali se i due operatori hanno il commutatore eguale ad una costante.

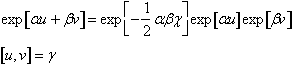(38)

La (39) si dimostra confrontando termine a termine gli sviluppi in serie del primo e del secondo membtro.

Si utilizzano poi le seguenti relazioni

(39)

Tali relazioni si dimostrano ancora tramite lo sviluppo in serie degli esponenziali e sfruttando le proprietà degli stati coerenti (15).

Nella (38) possiamo reintrodurre gli operatori posizione e quantità di moto ottenendo

(40)

Nella (40) abbiamo introdotto le funzioni del tempo x_c(t) e p_c(t) che esprimono il moto classico.

In ultimo utilizzando di nuovo l'identità operatoriale (39) e la seguente proprietà, ancora dimostrabile tramite sviluppo in serie

(41)

si ottiene come risultato finale

(42)

E' interessante notare come la funzione d'onda di uno stato coerente si ottenga dalla quella dello stato fondamentale centrando la gaussiana sulla posizione della particella definita ad ogni istante dall'equazione oraria classica e motiplicando per un fattore di fase proporzionale alla quantità di moto definita ad ogni istante dall'equazione oraria classica. Il fattore di oscillazione temporale corrisponde all'azione classica. a meno di una costante additiva che introduce un fattore di fase inessenziale. Infatti

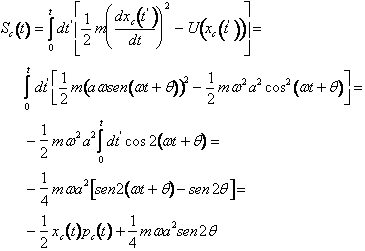(43)

Gli stati coerenti coincidono pertanto con gli stati quasiclassici introdotti precedentemente.