Il punto di massima distanza dei pianeti dal sole è detto afelio, mentre il punto di minima distanza è detto perielio. La linea ideale che congiunge afelio e perielio è detta linea degli apsidi. Le orbite presentano modeste eccentricità.

Per l'eccentricità e di un ellisse valgono le seguenti relazioni:

, con a = semiasse maggiore; b = semiasse minore (da cui )

, con c = semidistanza focale (distanza centro/fuoco) = R_max - a = a - R_min

da cui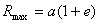 

Se ne deduce che il semiasse maggiore è pari alla media aritmetica della distanza massima e minima  mentre il semiasse minore è pari alla media geometrica delle suddette distanze

seconda legge di Keplero

Il raggio vettore che congiunge il centro del sole al centro dei pianeti descrive aree uguali in tempi uguali

La conseguenza più notevole di questa legge è che la velocità di rivoluzione dei pianeti intorno al sole non è costante, ma varia in relazione alla distanza, in modo che i pianeti accelerano avvicinandosi al perielio, mentre rallentano nel tratto che va da perielio ad afelio (in corrispondenza degli apsidi l'accelerazione è nulla, mentre la velocità è minima in afelio e massima in perielio). 

È possibile capire tale comportamento ricordando il principio fisico noto come costanza del momento angolare o momento della quantità di moto (mvr = k).

Essendo infatti m, massa del pianeta, costante v ed r devono essere inversamente proporzionali.

terza legge di Keplero

I quadrati dei tempi di rivoluzione (P) di ciascun pianeta sono proporzionali ai cubi del raggio medio dell'orbita (R) P = K R

Poiché si può dimostrare che il raggio medio dell'orbita è pari al semiasse maggiore a dell'ellisse la relazione può essere scritta    P = K a

L'ellisse è una curva simmetrica. Se consideriamo due punti P e P* disposti simmetricamente sull'ellisse possiamo osservare come la loro distanza media da un fuoco F sia pari a  (FP + FP*)/2. Ma per ragioni di simmetria la distanza FP* del secondo punto dal primo fuoco è uguale alla distanza F'P del primo punto dal secondo fuoco. La distanza media è perciò pari alla semisomma delle distanze di un punto dai due fuochi. Nell'ellisse la somma delle distanze di un punto dai due fuochi vale 2a per costruzione e quindi la distanza media vale a (cvd).

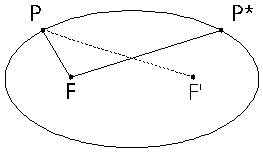
La conseguenza di tale legge è che passando da un pianeta più interno (più vicino al sole) ad uno più esterno, la velocità di rivoluzione non è inversamente proporzionale al raggio (come avviene all'interno di una stessa orbita), ma al suo quadrato. Assumendo infatti che la velocità di rivoluzione media sia pari al rapporto tra la lunghezza dell'orbita approssimata come circolare (2pR) ed il periodo di rivoluzione (P)   . Sostituendo opportunamente nella terza di Keplero si ottiene

La terza legge di Keplero, come del resto anche le prime due, può essere dedotta per via teorica dalla legge di gravitazione universale.

Essendo infatti la terra in equilibrio dinamico intorno al sole, la forza centripeta (gravitazionale) deve essere perfettamente bilanciata dalla forza centrifuga. La prima è espressa dalla legge di gravitazione universale, mentre la seconda è espressa dalla seconda legge della dinamica

   

con  m_s massa del sole e  m_t massa della terra

Eguagliando i due secondi membri e nell'ipotesi che la  massa gravitazionale della terra, che compare nella legge di gravitazione, abbia lo stesso valore della sua massa inerziale, che compare nella seconda legge della dinamica, si ottiene

Approssimando ora le orbite planetarie a delle circonferenze ed indicando con R il raggio medio dell'orbita terrestre e con V la sua velocità media, il valore della sua accelerazione è pari a   

  

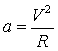
Sostituendo opportunamente nella precedente e semplificando otteniamo

Sostituendo infine alla velocità media il rapporto tra la lunghezza dell'orbita (al solito approssimata come circolare 2pR) ed il periodo di rivoluzione (P) , la relazione diventa

ed in definitiva

dove è la costante di proporzionalità che compare nella terza legge di Keplero. Tale valore è in realtà approssimato, in quanto non è esatto affermare che i pianeti orbitano intorno al sole. Newton ha infatti dimostrato che due corpi che si attraggono gravitazionalmente ruotano intorno ad un baricentro comune. Le distanze dei due corpi dal baricentro risultano inversamente proporzionali alle relative masse. Così se indichiamo con R_s ed R_t la distanza del sole e della terra dal baricentro comune, vale la seguente relazione.

M_s R_s = M_t R_t

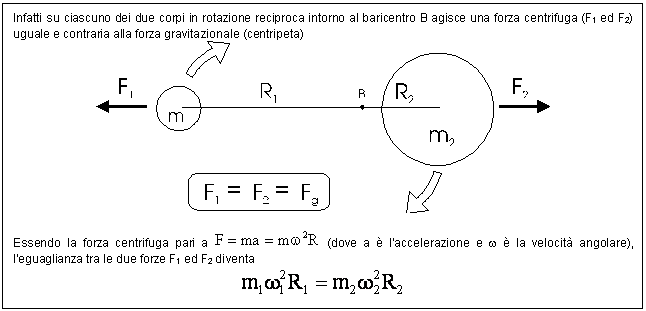
Il fatto che comunemente si accetti di considerare il moto planetario come un movimento dei pianeti intorno al sole è dovuto all'elevato valore della massa solare, enormemente più grande di quella di qualsiasi altro pianeta. In tal modo la distanza del sole dal baricentro comune è talmente piccola che il baricentro viene quasi a coincidere con il centro del sole.  La terza legge di Keplero rappresenta perciò una approssimazione, anche se molto buona della situazione reale. Infatti se si tiene conto anche della massa dei pianeti e non solo della massa del sole la relazione diventa

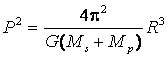
Si vede in tal modo che la costante di proporzionalità contiene la somma della massa del sole e della massa del pianeta preso in considerazione, così che essa è leggermente diversa per ciascun pianeta. Se si tiene però conto del fatto che la massa dei pianeti è trascurabile rispetto alla massa del sole, l'errore commesso è accettabile.

Il risultato corretto può essere ottenuto introducendo la massa ridotta. Si può infatti dimostrare che la condizione di equilibrio dinamico tra due corpi che ruotano intorno al baricentro comune rimane inalterata se allontaniamo il corpo di massa minore m₁ portandolo ad una distanza dal baricentro pari a R = R₁ + R₂, a patto di assegnargli una massa minore, detta appunto massa ridotta pari a . Infatti se , avremo anche ed anche . Moltiplicando ora entrambi i membri per m₂ e riordinando otterremo

Così la forza centrifuga del corpo di massa minore diventa

che, eguagliata alla forza gravitazionale

  

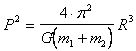
La relazione così ottenuta è d'altra parte molto utile per calcolare le masse dei pianeti una volta nota la massa solare, le loro distanze medie dal sole (R) e i loro periodi di rivoluzione (P).

Nel caso in cui si esprimano i periodi di rivoluzione ed i semiassi maggiori in unità terrestri (anni terrestri ed UA) la relazione diviene particolarmente semplice.

Ad esempio, sapendo che Giove dista dal sole 5,2 UA, è possibile calcolare agevolmente il suo periodo di rivoluzione in anni terrestri

La terza di Keplero può essere infine utilizzata per calcolare le masse di corpi in rotazione reciproca, come ad esempio sistemi di stelle doppie, mettendola a sistema con la relazione che lega le masse alle rispettive distanze dal baricentro comune.

Ad esempio, sapendo che il Sole dista circa 30.000 al dal centro galattico e percorre un'intera orbita intorno ad esso alla velocità di circa 250 km/s in un periodo di circa 230 milioni di anni, è possibile, trattando in prima approssimazione l'intera galassia come un sistema kepleriano, stimarne la massa, la quale risulta essere circa 200 miliardi di volte superiore a quella del Sole.

Calcolo alternativo

Consideriamo la condizione di equilibrio del corpo di massa m₂ che ruota intorno al baricentro B alla distanza R₂, percorrendo nel tempo P la circonferenza 2R₂.

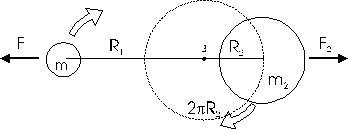
La sua forza centrifuga sarà pari a

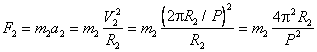
Eguagliamo ora la forza centrifuga F₂ alla  forza gravitazionale

da cui

Applicando lo stesso ragionamento al corpo m₁ si ottiene

Osservando ora che R = R₁ + R₂, si ottiene

da cui