|
|
| |
- Statistica
Analizzando una variabile statistica si può studiarne l'andamento attraverso una rappresentazione grafica. L'andamento di questo grafico indica chiaramente in quale situazione ricade la variabile studiata.
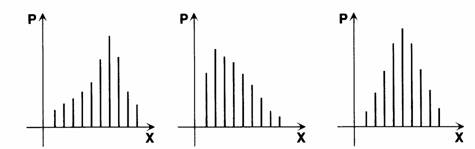
Fig. 1 Fig. 2 Fig. 3
La determinazione della simmetria può essere effettuata in due modi:
Si determina attraverso le relazioni che vi sono tra media, mediana e moda e la loro propria posiz 333i83d ione nel grafico.
- Se Media = Mediana = Moda la variabile è simmetrica (Fig. 3)
- Se Media < Mediana < Moda la variabile è asimmetrica negativa (Fig. 1)
- Se Media > Mediana > Moda la variabile è asimmetrica positiva (Fig. 2)
- Se Media Mediana Moda la variabile è asimmetrica
Nel caso in cui le relazioni fra media, mediana e moda non coincidano con nessuno dei casi precedenti, si passa al calcolo del seguente indice:
Mm xi - M)3 ni
- Se Mm la variabile è simmetrica (Fig. 3)
- Se Mm < 0 la variabile è asimmetrica negativa (Fig. 1)
- Se Mm > 0 la variabile è asimmetrica positiva (Fig. 2)
Per fare confronti invece si utilizza l'indice relativo:
a = Mm
![]() d
d
CURTOSI O NORMALITA' DI UNA VARIABILE STATISTICA
Il grafico di una distribuzione di una variabile statistica può assumere pendenze diverse a seconda che i valori siano più o meno concentrati attorno al valore medio.
![]()
![]()
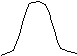 n n
n n
![]()
![]()
![]()
x x
(Fig. 4) (Fig. 5)
Si calcola per cui il seguente indice:
(xi - M)4 ni
![]() Mm N
Mm N
![]()
![]() b =
b =
d xi - M)2 ni
- Se b = 3 la variabile è normale
- Se b < 3 la variabile è iponormale (Fig. 5)
- Se b > 3 la variabile è ipernormale (Fig. 4)
- Programma
DICHIARAZIONE VARIABILI
Variabili di input
- int val : Numero di elementi da inserire (intero)
- float x[30] : Modalità (decimale)
- float n[30] : Frequenze (decimale)
Variabili di output
- float N : Collettivo statistico (decimale)
- float M, Me, Mo : Media, Mediana, Moda (decimale)
- float u3, u4 : indici assoluti per il calcolo della simmetria e della curtosi (decimale)
Variabili in uso nel pgm
- float Q[30], Qtot : Modalità per Frequenza e somma (decimale)
- int scheda,modo : Variabili per l'uso della grafica
- char rchar[30] : Stringa di caratteri utilizzata durante la visualizzazione del grafico
- int i,j,cont : Variabili per cicli e controlli (intero)
DESCRIZIONE DEL PGM
Immissione dati
L'inserimento del numero di elementi avviene con il controllo,che richiede l'inserimento se è stato riscontrato un errore, e la stessa cosa avviene con l'inserimento delle modalità e delle rispettive frequenze. Poi stampa a video la tabella di giuste dimensioni con il collettivo statistico. Durante l'esecuzione del ciclo trova anche la moda e gli x*n. Finito il ciclo tro vala media e la mediana e stampa tutto a video.
Simmetria
Metodo qualitativo
In base alle relazioni tra media, mediana e moda, dopo diversi controlli con le istruzioni 'if' e 'else', stampa a video il caso specifico.
Metodo quantitativo
Calcola e stampa il valore dell'indice Mm (u3) e in base a quest'ultimo trova il caso specifico e lo stampa.
Normalità o Curtosi
Calcola e stampa il valore dell'indice b (u4) e in base a quest'ultimo trova il caso specifico e lo stampa.
Grafica
La sessione di grafica inizia dopo aver premuto INVIO e disegna gli assi, le frecce, scrive il titolo in base alla normalità, scrive i nomi degli assi e salva nelle variabili 'u3' e 'u4' le costanti di entrambi (sapendo lo spazio in pixel a disposizione per il disegno). Disegna la scala sull'asse x con un ciclo e stampa i rispettivi valori. Lo stesso avviene con l'asse y, e in fine vengono disegnati i punti a dispersione e le linee corrispondenti che cadono sull'asse delle ascisse.
-Listato del programma
* Croci Jvan 4^ A Informatica 11-12-2000 *
// Input: Variabile statistica.
// Output: Simmetria (con i due metodi), Normalit., Grafico.
#include<conio.h>
#include<stdio.h>
#include<math.h>
#include<values.h>
#include<graphics.h>
int val; // Numeri inseriti
float x[30]; // x
float n[30]; // n
float N=0; // Collettivo statistico
float M=0,Me=0,Mo=0; // Media, Mediana, Moda
float u3=0,u4=0; // variabili per la simmetria e normalit.
float Q[30],Qtot=0; // x*n
int scheda,modo; // Variabili di grafica
char rchar[30]; //
int i=0,j=0,cont=0; // Variabili ausiliarie
void main(void)
while(val<=1 || val>30); // Controllo sul numero immesso
gotoxy(1,7);
printf(" ÉÍÍÍÍÍÍÍÍÍËÍÍÍÍÍÍÍÍÍ»"); // Disegna la tabella
printf("\n º x º n º");
printf("\n ÌÍÍÍÍÍÍÍÍÍÎÍÍÍÍÍÍÍÍ͹");
for(i=0;i<val;i++)
printf "\n º ");
for(i=0;i<val;i++)
else
cont=0;
}
while(cont>0);
do
else
cont=0;
}
while(cont>0);
if(n[i]>j)
N+=n[i]; // Collettivo statistico
Q[i]=x[i]*n[i]; // x*n
Qtot+=Q[i]; // Somma xn
} // Fine del ciclo di immissione dati
gotoxy(5,10+val);
printf("ÈÍÍÍÍÍÍÍÍÍÎÍÍÍÍÍÍÍÍ͹");
printf("\n º º");
printf("\n ÈÍÍÍÍÍÍÍÍͼ"); // Fine tabella
gotoxy(17,11+val);
printf("%.3f",N);
i=0;
do
while(Me<0.5);
Me=x[i-1]; // Mediana
M=Qtot/N; // Media
gotoxy(37,9);
printf(" La media S: %.3f",M);
gotoxy(37,10);
printf(" La mediana S: %.3f",Me);
gotoxy(37,11);
printf(" La moda S: %.3f",Mo);
//----- ----- --------- ----- ------ SIMMETRIA -------- ----- ------ --
//----- ----- ---------------- METODO QUALITATIVO ----- ----- --------- ----- ------
gotoxy(1,14+val);
printf(" SIMMETRIA: metodo qualitativo");
if(M==Me && Me==Mo)
else
else
else
}
}
//----- ----- ---------------- METODO QUANTITATIVO ----- ----- --------- ----- ------
printf("\n\n SIMMETRIA: metodo quantitativo");
for(i=0;i<val;i++)
u3+=(pow((x[i]-M),3))*n[i];
u3=u3/N;
printf("\n æ= %.3f",u3); // Indice æ3
if(u3==0)
else
else
}
//----- ----- --------- ----- ------ NORMALITA' -------- ----- ------ -
printf("\n\n CURTOSI o NORMALITA'");
u3=0;
for(i=0;i<val;i++)
u4=u4/N;
u3=pow((u3/N),2);
u4=u4/u3;
printf("\n á= %.3f",u4); // Indice á2
if(u4==3)
else
else
}
//----- ----- --------- ----- ------- GRAFICA -------- ----- ------ ---
printf("\n\n Per visualizzare il grafico premere il tasto INVIO ");
getch
detectgraph(&scheda,&modo);
initgraph(&scheda,&modo,"c:\\borlandc\\bgi");
clrscr
setfillstyle
floodfill
line(100,440,100,20); // Asse y =410
line(90,430,540,430); // Asse x =440
line(95,25,100,20);
line(105,25,100,20); // Freccia
line(95,25,105,25);
line(535,425,540,430);
line(535,425,535,435); // Freccia
line(535,435,540,430);
settextstyle
setcolor(BLUE);
outtextxy(130,5,"Distribuzione");
if(cont==0)
outtextxy(320,5,"NORMALE");
else
u3=420; // Costante asse x
u4=390; // Costante asse y
setcolor(15);
settextstyle(1,0,1); // Nomi assi
outtextxy(550,450,"x");
outtextxy(40,10,"n");
setcolor
cont=u3/x[val-1];
settextstyle
for(i=0;i<val;i++)
cont=u4/j;
settextstyle
for(i=0;i<val;i++)
setcolor(4);
setfillstyle(1,4);
j=u3/x[val-1];
for(i=0;i<val+1;i++)
setcolor
getch
// Termine pgm
- Esempio di output
*** SIMMETRIA E NORMALITA' DI UNA VARIABILE STATISTICA ***
Quanti numeri vuoi inserire ? 5
╔══════╦══════╗
║ x ║ n ║
╠══════╬══════╣ La media è: 24.300
║ 5 ║ 10 ║ La mediana è: 25.000
║ 15 ║ 25 ║ La moda è: 25.000
║ 25 ║ 35 ║
║ 35 ║ 22 ║
║ 45 ║ 8 ║
╚══════╬══════╣
║ 100.000 ║
╚══════╝
SIMMETRIA: metodo qualitativo
M#Me#Mo => ASIMMETRIA
SIMMETRIA: metodo quantitativo
µ= 59.214
µ>0 => ASIMMETRIA POSITIVA
CURTOSI o NORMALITA'
ß= 0.024
ß<3 => distribuzione IPONORMALE
Per visualizzare il grafico premere il tasto INVIO
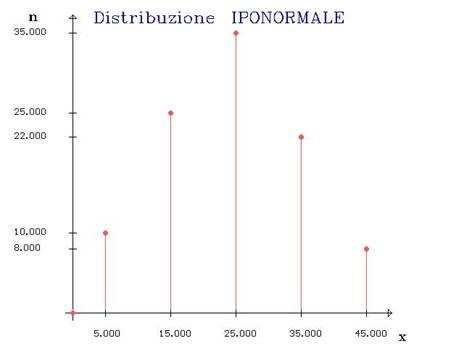
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025