|
|
| |
TEOREMA DI TALETE
T. Le due classi di segmenti corrispondenti individuati da un fascio di rette parallele su due trasversali sono direttamente proporzionali.
Osservato che la corrispondenza che associa i segmenti AB, BC, CD,... della trasversale r rispettivamente ai segmenti A'B', B'C', C'D',... della trasversale r' è biunivoca, per pro 949h79j vare l'enunciato applichiamo il primo criterio di proporzionalità. Pertanto dobbiamo dimostrare:
che a segmenti uguali di r corrispondono segmenti uguali di r' (Fig. 1);
che alla somma di due segmenti, presi su r, corrisponde, su r', il segmento somma dei due segmenti corrispondenti a quelli fissati su r (Fig. 2).
1) Sia AB=CD. Vogliamo provare che è pure A'B'=C'D'. Dette a,b,c,d le rette del fascio passanti rispettivamente per i punti A,B,C,D, conduciamo per A e per C le parallele alla r' che intersecano la prima la retta b in P e la seconda la retta d in Q. I triangoli ABP, CDQ sono uguali perchè hanno AB=CD per ipotesi, ABP=CDQ (angoli) perchè corrispondenti rispetto alle parallele b,d tagliate da r, BAP=DCQ (angoli) perchè corrispondenti rispetto alle parallele AP,CQ tagliate da r. Segue da ciò l'uguaglianza dei segmenti AP,CQ. D'altra parte si ha pure AP=A'B' e CQ=C'D' come lati opposti dei parallelogrammi APB'A' e CQD'C'; il che porta a concludere che si ha A'B'=C'D'.
2)Sia GH=CD + EF. Vogliamo dimostrare che G'H', corrispondente di GH, è la somma di C'D' ed E'F', rispettivamente corrispondenti di CD ed EF. Per le ipotesi fatte esiste un punto K del segmento GH che lo divide in due segmenti GK e KH rispettivamente uguali a CD ed EF. Sia k la retta del fascio passante per K e che interseca in K' la trasversale r'. Poichè abbiamo stabilito che a segmenti uguali di r corrispondono segmenti uguali di r', da GK=CD e KH=EF segue che G'K'=C'D' e K'H'=E'F'. Pertanto si conclude che G'H'=G'K' + K'H'=C'D' + E'F'
COROLLARIO DI TALETE
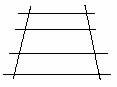
C. Una retta parallela ad un lato di un triangolo determina sugli altri due lati, o sui loro prolungamenti, segmenti proporzionali. (Fig.1)
Sia ABC un triangolo; conduciamo una parallela al lato BC, che interseca le rette AB, AC nei punti D, E. Per il vertice A tracciamo la parallela p a BC. Se applichiamo il teorema di Talete alle 3 parallele p, DE, BC e alle loro trasversali AB, AC abbiamo: AB:AC=AD:AE=DB:EC.
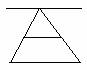
TEOREMA INVERSO DEL COROLLARIO DI TALETE
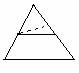
T. Una retta che determina su due lati di un triangolo, o sui loro prolungamenti, segmenti proporzionali, è parallela al terzo lato (inverso del precedente corollario). (Fig.2)
Dato un triangolo ABC, si consideri una retta che interseca le rette AB ed AC rispettivamente nei punti D ed E, tali che sia AB:DB=AC:EC. Vogliamo dimostrare che DE è parallela a BC. Ragioniamo per assurdo e supponiamo che DE non sia parallela a BC. In tal caso esisterebbe una retta DF, passante per D e parallela a BC, che incontrerebbe la retta AC in un punto F distinto da E. Per il precedente corollario si avrebbe: AB:DB=AC:FC. Confrontando tale proporzione con quella fornitaci dall'ipotesi del teorema si cade in assurdo.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026