|
|
| |
a)
![]()
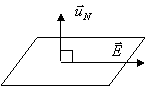
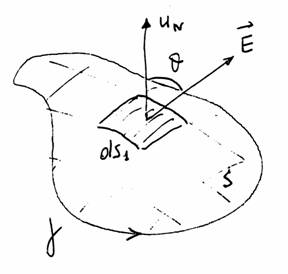 Dato il percorso chiuso
Dato il percorso chiuso ![]() si sceglie un verso di
percorrenza, es. antiorario;
si sceglie un verso di
percorrenza, es. antiorario;
b)
avvitando nel verso prescelto ,
con la mano destra, il pollice determina il verso della normale alla superficie
![]() ;
;
c)
il flusso attraverso 838g63i un elemento ![]() , di
, di ![]() , vale :
, vale :
![]()
Sommando
tutti i contributi ![]() si ottiene
si ottiene
il
flusso ![]() del campo
del campo ![]() attraverso
attraverso ![]() :
:
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
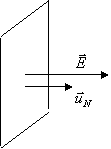
![]() parallelo, concorde
parallelo, concorde ![]() ,
, ![]() , flusso USCENTE
, flusso USCENTE
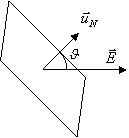
![]() parallelo, discorde
parallelo, discorde ![]() ,
, ![]() , flusso ENTRANTE
, flusso ENTRANTE
La legge di Gauss
asserisce che il flusso di ![]() attraverso una
superficie chiusa è uguale alla carica contenuta nella superficie divisa
attraverso una
superficie chiusa è uguale alla carica contenuta nella superficie divisa ![]() .
.
![]() (10)
(10)
dove ![]() è la densità di carica
volumetrica:
è la densità di carica
volumetrica:
![]()
Si
verifica facilmente la legge di Gauss nel caso del campo ![]() creato da una carica
puntiforme q, calcolando il flusso
attraverso una sfera di raggio r con
centro su q.
creato da una carica
puntiforme q, calcolando il flusso
attraverso una sfera di raggio r con
centro su q.
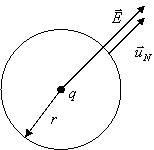
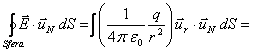
Dato
che ![]() ha lo stesso valore su
tutti i punti della sfera:
ha lo stesso valore su
tutti i punti della sfera:
![]()
C.V.D.
(N.B. ![]() è
stato espressa come
è
stato espressa come![]() , proprio per avere un risultato che non contenga altri
costanti, eccetto
, proprio per avere un risultato che non contenga altri
costanti, eccetto ![]() .)
.)
Si dimostra che vale anche per una superficie di forma qualsiasi purché q sia interna ad essa.
La legge di Gauss che in forma integrale risulta:
![]() (11)
(11)
può essere espressa in forma differenziale facendo uso del:
Teorema della
Divergenza: (o Green-Gauss) che asserisce che il
flusso di un vettore (![]() ) attraverso
) attraverso
una
superficie chiusa S è uguale all'integrale, esteso al volume racchiuso da S,
della divergenza di![]() .
.
N.B. divergenza di ![]() = div
= div ![]() =
= ![]() Si veda in proposito
anche l'appendice A.
Si veda in proposito
anche l'appendice A.
![]()
per la (11)
![]()
se v arbitrario, anche gli integrali sono uguali; risulta:
![]() (12)
(12)
Questa è la legge di Gauss in forma differenziale. Essa costituisce anche la prima legge di Maxwell. Un campo la cui divergenza è nulla , è detto SOLENOIDALE.
N.B. si trasforma una forma "integrale" ![]() forma "differenziale"
cha da un'informazione puntuale.
forma "differenziale"
cha da un'informazione puntuale.
Anche la proprietà del campo elettrico di essere conservativo cioè:
![]()
può essere espresso in forma differenziale facendo uso del
Teorema di Stokes:
che asserisce che la circuitazione di un vettore (![]() ) lungo una linea chiusa
è
) lungo una linea chiusa
è
uguale al flusso del rotore di ![]() attraverso la
superficie che ha per contorno
attraverso la
superficie che ha per contorno ![]() .
.
N.B. rotore di ![]() = rot
= rot ![]() =
= ![]()
![]()
Nel nostro caso, poiché il primo membro è nullo risulta:
![]() (14)
(14)
Condizione necessaria (ma non sufficiente) affinché un campo sia conservativo è che il rotore sia nullo.
Esempio: ![]() è un campo
conservativo, infatti:
è un campo
conservativo, infatti:
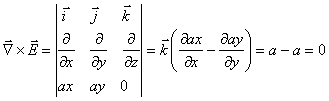
Il rotore è nullo e il dominio è semplicemente
connesso (si può ridurre la linea ![]() ad un punto senza
uscire dal dominio).
ad un punto senza
uscire dal dominio).
 Il campo creato ha andamento a
simmetria sferica. Si sceglie
Il campo creato ha andamento a
simmetria sferica. Si sceglie
come superficie gaussiana una
sfera. Su di essa ![]() , parallelo a
, parallelo a ![]() .
.
![]()
da cui:
![]() (15)
(15)
![]() ha la stessa
espressione che avrebbe il campo creato da una carica posta al centro della
sfera.
ha la stessa
espressione che avrebbe il campo creato da una carica posta al centro della
sfera.
Se consideriamo
una superficie gaussiana all'interno della sfera ![]() = 0 perché q = 0 al suo interno.
= 0 perché q = 0 al suo interno.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Per ragioni di simmetria
Per ragioni di simmetria
![]() piano (salvo i bordi). Si sceglie un parallelepipedo o un
cilindro.
piano (salvo i bordi). Si sceglie un parallelepipedo o un
cilindro.
![]()
Poichè sulle superfici laterali ![]()
![]()
![]() .
.
Le basi sono due:
![]()
da cui:
![]() (16)
(16)
dove ![]() densità di carica
superficiale.
densità di carica
superficiale.
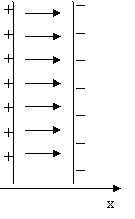
Per la sovrapposizione degli effetti, il campo risulta doppio di quello di un piano.
![]() (17)
(17)
La suddetta struttura costituisce un condensatore piano.
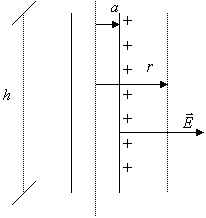 Vista di lato: Il
campo ha un andamento radiale. Si sceglie come superficie gaussiana un
cilindro concentrico di raggio r e altezza h.
Vista di lato: Il
campo ha un andamento radiale. Si sceglie come superficie gaussiana un
cilindro concentrico di raggio r e altezza h.
![]()
Il
contributo delle basi risulta = 0 perché ![]()
![]() .
.
![]()
Da cui:
 Vista dall'alto:
Vista dall'alto: ![]() (18)
(18)
Dove:
![]() densità di carica
lineare
densità di carica
lineare
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025