FOTOMETRIA - Intensità luminosa - Calcolo quantità fotometriche solari

Ricordiamo che 1 steradiante (sr) è l'angolo solido sotto il quale un osservatore posto al centro di una superficie sferica vede una calotta sferica di superficie R . Essendo l'intera superficie sferica pari a 4pR , l'intero angolo solido sarà pari a 4p steradianti.

Nel Sistema SI l'unità fotometrica fondamentale è la candela (cd), che misura l'intensità I di una sorgente luminosa. Essa viene naturalmente definita in funzione di un campione luminoso, convenzionalmente individuato. Un tempo la candela veniva definita come 1/60 dell'intensità luminosa prodotta da 1 cm di corpo nero a 2042°K (temperatura di fusione del platino). Nel 1979 la XVI Conferenza Generale dei Pesi e delle Misure definì la candela come l'intensità luminosa di una sorgente di potenza 1/683 W/sr che emette una radiazione monocromatica di 5,40 10¹⁴ Hz (l = 555,016 nm)

Flusso luminoso F

Si definisce flusso luminoso F il prodotto dell'intensità luminosa per l'angolo solido W attraverso cui la luce diffonde. La sua unità di misura è la candela steradiante (cd sr) o lumen (lm).

Una sorgente luminosa puntiforme che diffonda luce in tutte le direzioni (sull'intero angolo solido) produce un flusso luminoso di 4p lumen.

Brillanza B

Per sorgenti estese (non puntiformi) viene definita la brillanza B (o luminanza o splendore) come l'intensità di emissione dell'unità di superficie in direzione ortogonale alla superficie stessa. Nel caso la direzione di emissione formi un angolo j con la direzione normale alla superficie, la superficie emittente va moltiplicata per cosj. La sua unità di misura è la candela/m (o nit (nt), nel Sistema SI) o candela/cm (o stilb (sb), nel sistema cgs).

Illuminamento E

Per misurare gli effetti della luce che colpisce una superficie S si definisce l'illuminamento E, come il flusso che colpisce l'unità di superficie S, disposta perpendicolarmente ai raggi luminosi. La sua unità di misura è il lumen/m (o lux (lx), nel sistema SI) o lumen/cm (nel sistema cgs). Nel caso il flusso formi un angolo q con la direzione normale alla superficie, il suo valore va moltiplicato per cosq

Una sorgente puntiforme di intensità I posta al centro di una superficie sferica di raggio R incide su di essa con un flusso pari a 4pI lumen. L'unità di area di tale superficie viene perciò illuminata da

Possiamo definire quindi 1 lux come l'illuminamento a cui è sottoposta una superficie di 1 m posta alla distanza di 1 m da una sorgente di 1 candela che la illumini ortogonalmente con un flusso di 1 lumen.

La relazione precedente mostra anche come l'illuminamento a cui è sottoposta una superficie è direttamente proporzionale all'intensità luminosa della sorgente ed inversamente proporzionale al quadrato della sua distanza.

Se due sorgenti luminose di diversa intensità ( I e I ) e a diversa distanza (R e R ) illuminano una superficie allo stesso modo (E = cost) allora deve valere

e anche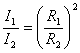

Come è già stato detto uno degli scopi della fotometria è quello di correlare il flusso luminoso alla potenza (energia per unità di tempo) trasportata dal fascio di radiazione ottica.

Il primo problema che si presenta è legato al fatto che il nostro occhio non è egualmente sensibile a tutte le lunghezze d'onda ottiche, ma presenta un massimo di sensibilità per la luce di 0,555 m (giallo-verde).

Si definisce a tal proposito il coefficiente di visibilità K_l come il rapporto tra il flusso luminoso ed il corrispondente flusso energetico (in watt) portati da una radiazione monocromatica di lunghezza l

Il valore massimo di tale coefficiente si ha appunto per la radiazione di 0,555m e vale

A parità di energia trasportata dal raggio luminoso la sensazione ottica diminuisce di intensità man mano che ci discostiamo da tale lunghezza d'onda. Per determinare l'entità di tale diminuzione si calcola il cosiddetto fattore di visibilità relativa (V_l) di una radiazione ottica di lunghezza d'onda l

Per determinare il valore di tale fattore per le diverse lunghezze d'onda visibili è possibile misurare e rapportare l'energia portata da un fascio di radiazione a 0,555m e l'energia trasportata da un fascio di radiazione di lunghezza d'onda l, stimato di egual intensità luminosa (in grado di generare cioè la medesima sensazione ottica).

Il fattore di visibilità relativa varrà dunque 1 per la radiazione di lunghezza 0,555m e assumerà valori via via inferiori per le altre lunghezze d'onda ottiche, azzerandosi intorno a 0,4 e 0,7m

Possiamo provare a stimare la visibilità media sovrapponendo alla curva una gaussiana normalizzata (media M = 0, scarto quadratico medio s = 1, ordinata massima F(M) = = 0,39894, area totale = 1) in cui i valori estremi (0,4 - 0,7) coincidano con i valori standardizzati -3,5 e +3,5 corrispondenti ad una area praticamente pari ad 1 (> 0,999).

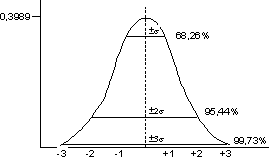
L'ordinata media è pari all'area (1) diviso l'ascissa relativa (+3,5 - (-3,5) = 7) e vale quindi 1/7. Possiamo ora impostare una proporzione tra la gaussiana e la curva di visibilità tra le corrispondenti ordinate massime e medie

0,39894 : 1 = 1/7 : x

che ci fornisce una visibilità media di circa il 35,8 %

La relazione che lega il flusso luminoso alla potenza P del fascio per unità di area ed alla sezione trasversale S del fascio è

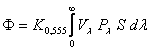
dove l'integrale viene esteso per consuetudine da zero ad infinito, ma si azzera al di fuori dell'intervallo di visibilità poiché in tal caso si annulla V_l

Calcolo quantità fotometriche solari

Integrando l'equazione di Planck per un corpo nero alla temperatura di 5778 °K (temperatura efficace del sole) da 0,39m a 0,72m si ottiene l'emissione ottica unitaria del sole, pari a 2,52 10 watt/m

Calcoliamo ora l'emissione ottica totale moltiplicando per la superficie solare (6,087 10¹⁸ m ), ottenendo 1,534 10 watt. Essendo l'energia portata su tutte le lunghezze d'onda del visibile, utilizziamo il fattore medio di visibilità relativa pari a 0,37 per calcolare il fattore di visibilità solare

il flusso del sole varrà allora

La sua intensità luminosa sarà

la sua brillanza

mentre, ricordando che la terra dista dal sole R = 1,496 10¹¹ m, l'illuminamento solare cui è sottoposta la terra (al di fuori dell'atmosfera) sarà

Fotometria stellare

La prima misura dell'intensità luminosa delle stelle fu naturalmente eseguita confrontando le stelle per mezzo dell'occhio (luminosità visuale). Così Ipparco, nel II sec. a.C., aveva fissato una scala empirica, detta delle magnitudini apparenti (m), comprendente 6 gradi di luminosità. Secondo tale scala la stella più luminosa del cielo risultava essere di prima magnitudine (m = 1) ed era 5 volte più luminosa di una (appena visibile) di sesta magnitudine (m = 6).

Le magnitudini sono dette apparenti poiché il loro valore, a parità di intensità luminosa, dipende anche dalle distanza delle stelle.

Una profonda revisione si ebbe nella seconda metà dell'ottocento quando si scoprì che la sensazione visiva (S) non è direttamente proporzionale all'intensità (l) dello stimolo luminoso percepito, ma al suo logaritmo. Tale relazione viene espressa dalla legge di Fechner e Weber.

che, nel caso di una stella, lega la magnitudine apparente m, alla luminosità apparente l (misurata in genere in lux)

C è una costante (costante di zero) il cui valore dipende dalle unità di misura usate per esprimere la luminosità e dal valore assunto convenzionalmente come zero per la scala delle magnitudini

Poichè tramite registrazioni fotometriche (Herschel) una stella di prima magnitudine risultò essere in realtà 100 volte più luminosa di una di 6 magnitudine, la costante k assume il valore -2,5. Infatti

e quindi

k = -2,5

La relazione fondamentale della fotometria stellare diventa quindi (relazione di Pogson)

e quindi

passando infine all'antilogaritmo

Se dobbiamo ad esempio confrontare la luminosità di Sirio m = - 1,45 con quella di Aldebaran (m = 0,85) troveremo

Sirio dunque è apparentemente circa 8,3 volte più luminoso di Aldebaran.

Per ogni grado di magnitudine (m - m = 1) la luminosità apparente aumenta di circa 2,512 volte. Come per ogni scala convenzionale anche nel caso delle magnitudini apparenti è necessario fissare un punto zero.

Viene dunque definita di magnitudine visuale apparente zero (m_vis = 0) una stella che produca (al di fuori dell'atmosfera) un illuminamento di 2,67 10 lux.

La costante di zero assume in tal caso il valore

C_V

Ricordando che il sole fornisce un illuminamento di 1,34 10 lux, possiamo allora calcolarne facilmente la magnitudine apparente (visuale)

La magnitudine visuale è naturalmente correlata al flusso ottico (spettro visibile) che ci proviene dalle stelle. Quando invece si misura il flusso energetico su tutte le lunghezze d'onda, si ottiene la magnitudine bolometrica. Anche in questo caso è necessario fissare un punto zero. Viene definita di magnitudine bolometrica apparente zero (m_bol = 0) una stella che produca (al di fuori dell'atmosfera) una potenza unitaria di 2,56 10 erg/(s cm

La costante di zero assume in tal caso il valore

C_b

Ricordando che il sole fornisce una potenza unitaria (costante solare) di 1,368 10 erg/(s cm ), possiamo calcolarne la magnitudine apparente (bolometrica)

Qualora si conosca la distanza R di una stella dalla terra se ne può calcolare anche la luminosità intrinseca L (espressa come intensità luminosa o come flusso luminoso)

Sapendo ad esempio che Sirio dista 8,6 al (8,136 10¹⁶ m) e che la sua magnitudine apparente vale m = - 1,45 determiniamo:

- l'illuminamento, che è 2,512 = 3,8 volte superiore a E_o e pari quindi a circa 10 lux

- il flusso, pari a

- l'intensità luminosa, pari a

scopriamo così che Sirio è 21,6 volte più luminoso del sole

Come si vede è scomodo confrontare le luminosità intrinseche delle stelle utilizzando lumen e candele. Si è perciò convenuto di misurare la luminosità intrinseca di una stella utilizzando la scala di Ipparco, dopo aver azzerato le differenze di distanza portando tutte le stelle a 10 parsec.

La magnitudine apparente che una stella verrebbe a possedere se fosse posta a 10 parsec è detta magnitudine assoluta M.

Così una stella di luminosità intrinseca L (flusso) e distanza R, che presenta un luminosità apparente l (illuminamento) pari a

posta a 10 parsec presenterebbe una luminosità apparente l pari a

dove k è un coefficiente (pari a 3,0857 10 m/pc) che trasforma i parsec in m

Applicando la formula di Pogson a questi due valori di luminosità apparente, si ottiene

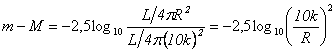
Essendo R/k la distanza della stella espressa in parsec, la relazione diventa

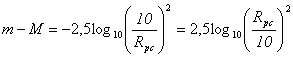
Essendo la quantità (m-M) correlata alla distanza della stella, essa viene detta modulo di distanza.

Sapendo che il sole dista dalla terra 1,496 10¹¹ m pari a 4,848 10 parsec, possiamo determinarne la magnitudine assoluta visuale e bolometrica

La magnitudine assoluta di Sirio (m = - 1,45 ; R = 2,64 pc) sarà

La magnitudine assoluta di Aldebaran (m = 0,85 ; R = 18,4 pc) sarà

Così la differenza di magnitudine assoluta tra Sirio e il Aldebaran è 1,44 - (-0,47) = 1,91

Scopriamo così che Sirio è in realtà circa 2,512 = 5,8 volte meno luminoso di Aldebaran.

Tenendo poi conto che la luminosità apparente che segna il punto zero della scala delle magnitudini apparenti è 2,67 10 lux (lumen/m ), possiamo trovare il corrispondente valore (M = 0) per la scala delle magnitudini assolute, calcolando la corrispondente luminosità intrinseca visuale a 10 parsec

corrispondenti ad un'intensità luminosa di 2,54 10 candele

Mentre, ricordando che il punto zero delle magnitudini apparenti bolometriche è 2,56 10 erg/(s cm ), la corrispondente luminosità intrinseca bolometrica a 10 parsec sarà

In questo modo la relazione di Pogson

può essere utilizzata anche per calcolare la magnitudine assoluta, sostituendo alle luminosità apparenti le luminosità intrinseche della stella e del punto zero

Magnitudine assoluta di 1 candela

Magnitudine apparente di 1 lux

Formula di Russell

La relazione di Pogson può essere utilizzata per ottenere una relazione tra la Magnitudine, la Temperatura ed il Raggio (in unità solari R ) di una stella. Indicando rispettivamente con M_V e M_V la magnitudine visuale assoluta di una stella e del sole possiamo scrivere

Per determinare l'emissione di una stella in corrispondenza di una certa lunghezza d'onda l possiamo ricorrere all'equazione di Planck che descrive il comportamento emissivo di un radiatore perfetto (corpo nero), fornendoci la quantità di energia (erg) emessa, per unità di tempo (s) e di superficie radiante (cm²), da un corpo alla temperatura T (K) in corrispondenza della lunghezza d'onda l (cm).

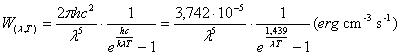
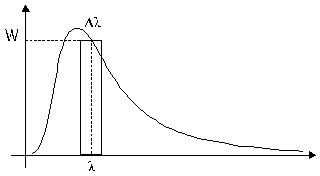
Possiamo ora stimare l'energia emessa nell'intorno della lunghezza d'onda l, calcolando l'area sottesa all'intervallo Dl centrato in l. In prima approssimazione esso è pari all'area del rettangolo avente base Dl e altezza W_(lT)

Nel nostro caso, dovendo valutare l'emissione nel visibile l ^{-10 cm, la relazione diventa}

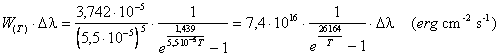
La luminosità assoluta visuale della stella sarà pari all'energia emessa nel visibile dall'intera superficie.

Sostituendo nella relazione di Pogson, otteniamo

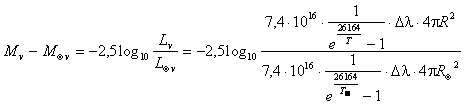
Ricordando che T 5778 °K, la relazione diventa

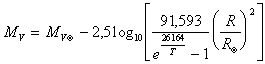
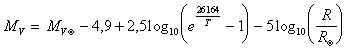
e assegnando al sole magnitudine visuale assoluta 4,82 otteniamo

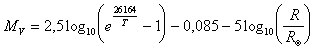
o, esplicitando il raggio,

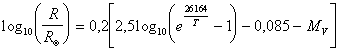
Se ora, in prima approssimazione, trascuriamo l'unità nella differenza dell'argomento del logaritmo otteniamo la classica relazione di Russell

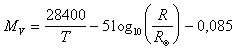
o, esplicitando il raggio,

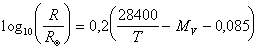
E' possibile costruire una relazione analoga che leghi la magnitudine bolometrica al raggio ed alla temperatura. Indicando rispettivamente con M_bol e M_bol la magnitudine bolometrica assoluta di una stella e del sole possiamo scrivere

Per determinare l'emissione di una stella in corrispondenza di tutte le lunghezze d'onda possiamo ricorrere all'equazione di Stefan-Boltzmann. che descrive il comportamento emissivo di un radiatore perfetto (corpo nero), fornendoci la quantità di energia (erg) emessa, per unità di tempo (s) e di superficie radiante (cm²), da un corpo alla temperatura T (°K) in corrispondenza di tutte le lunghezze d'onda e moltiplicarla per la superficie della stella 4pR². Essendo dunque

potremo scrivere

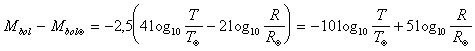
Assumendo infine per la temperatura e la magnitudine assoluta bolometrica del sole i valori T 5780 °K e M_bol = 4,75 si ottiene

Confrontiamo ora tale relazione con la relazione

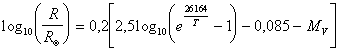
Eguagliando i due secondi membri ed esplicitando la differenza tra M_bol e M_V si ottiene

o, trascurando ancora l'unità nella differenza,

Il valore così ottenuto viene definito correzione bolometrica BC.

La correzione bolometrica viene in realtà calcolata tramite modelli più sofisticati relativi alle atmosfere stellari. Il valore zero della scala è stato convenzionalmente fissato in modo che sia BC = 0 per stelle con T_e = 6580 °K (tipo spettrale F5).

Indici di colore

Quando in astronomia iniziarono ad essere utilizzate le emulsioni fotografiche fu possibile ottenere anche valori di magnitudine fotografica (M_pg). I valori ottenuti sono in genere tra loro diversi in quanto l'occhio presenta un massimo di sensibilità nel giallo-verde, mentre la lastra fotografica nel blu-violetto. Applicando ad una macchina fotografica un filtro giallo si riesce a simulare la sensibilità dell'occhio umano e le magnitudini così ottenute sono dette fotovisuali (M_pv

Le magnitudini ottenute con un fotometro sono dette fotoelettriche. Le magnitudini fotoelettriche vengono determinate in corrispondenza di particolari intervalli di lunghezze d'onda. In genere si ottengono per l'ultravioletto (M_U o U) per il blu (M_B o B) e per il giallo (visuali) (M_Vo V) .

La magnitudine fotoelettrica B è correlabile alla magnitudine fotografica (M_B = M_pg + 0,11), mentre la magnitudine fotoelettrica V corrisponde alla magnitudine visuale o fotovisuale.

Le differenze nei valori di magnitudine misurati nei diversi intervalli di lunghezze d'onda sono importanti poiché sono correlabili alla temperatura superficiale di una stella. Infatti per la legge di Wien un corpo nero che aumenta la sua temperatura emette in proporzione sempre più energia verso le regioni a minor lunghezza d'onda (blu violetto). Così una stella molto calda presenterà una magnitudine nel blu minore della sua magnitudine visuale, mentre per una stella molto fredda avverrà l'opposto (valori minori di magnitudine corrispondono infatti a luminosità più elevate).

Un indice di colore molto usato è proprio fornito dalla differenza tra la magnitudine fotografica e la magnitudine visuale (o fotovisuale).

C = M_pg - M_pv = m_pg - m_pv

Un altro indice spesso utilizzato è l'indice B-V, dato dalla differenza della magnitudine fotoelettrica nel blu e nel visuale.

La relazione tra questi due indici è approssimativamente

C + 0,11 B-V

L'indice di colore ha il vantaggio di fornire i valori di temperatura di una stella (nell'ipotesi che essa irradi come un corpo nero) indipendentemente dalla conoscenza della distanza della stella e del suo raggio (e quindi del valore della sua superficie emittente).

Più basso è il valore di tale indice, più la stella emette nel blu e più elevata è la sua temperatura. L'indice di colore del sole è + 0,55, mentre l'indice di colore di una stella a 15.000°K è - 0,27.

Per costruire l'indice di colore si ricorre ad una formulazione approssimata della funzione di Planck che descrive il comportamento emissivo di un radiatore perfetto (corpo nero).

Poichè l'indice di colore viene costruito su lunghezze d'onda del visibile, intorno a 5 10^{-10 cm, la relazione diventa}

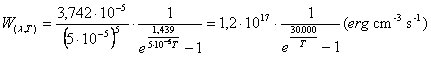
ed in tal caso è dunque possibile, per temperature inferiori ai 20.000 °K, trascurare l'unità nella differenza a denominatore ed utilizzare la seguente planckiana approssimata (approssimazione di Wien, per le basse temperature)

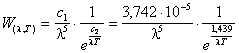
Siano ora m_l ed M_l la magnitudine apparente ed assoluta di una stella di raggio R e distanza D, misurate nella radiazione di lunghezza d'onda l

La luminosità assoluta della stella sarà pari a

e la sua magnitudine assoluta

La luminosità apparente della stella sarà pari a

e la sua magnitudine apparente

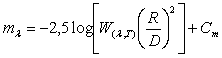
Se ora costruiamo l'indice di colore, come differenza tra le magnitudini (apparenti o assolute) a diverse lunghezze d'onda l e l , otteniamo

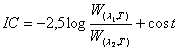
E' ora facile verificare che costruendo l'indice di colore con le magnitudini assolute si ottiene lo stesso risultato, indipendente sia da R che da D.

Sostituiamo ora la planckiana approssimata ed otteniamo

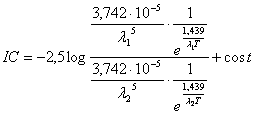
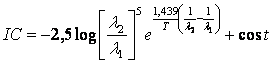
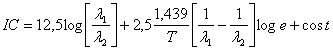
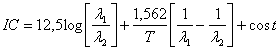
Se usiamo ad esempio

l ^{-5 cm, lunghezza di massima emissione nel blu}

l ^{-5 cm, lunghezza di massima emissione nella banda del visibile}

la relazione diventa

L'indice di colore viene poi tarato fissando la costante di zero in modo che IC = 0 per stelle di classe spettrale A0 (T 10.000°K). La costante di zero varrà quindi

cost = + 0,555

e la relazione diventa

ed in definitiva la temperatura di colore è pari a

Se invece utilizziamo

l ^{-5 cm, lunghezza di massima emissione nel blu}

l ^{-5 cm, lunghezza di massima emissione nella banda del visibile}

Si ottiene l'indice B-V del sistema fotoelettrico U-B-V di Morgan-Johnson

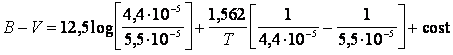
Anche in questo caso la taratura viene effettuata fissando la costante di zero in modo che B-V = 0 per stelle di classe spettrale A0 (T 10.000°K). La costante di zero varrà quindi cost = + 0,5 e la relazione diventa

ed in definitiva la temperatura di colore è pari a

Appendice

velocità della luce 2,99792458^.10 cm s 2,99792458^.10 m s carica dell'elettrone 4,80320680^. 10 u.e.s.  1,60217733^.10^{-19 C}

cost. di Boltzmann    1,380658^.10 erg °K 1,380658^.10 J °K

cost. di gravit. univers.    6,67259^.10 cm g s 6,67259^.10^{-11 m3} kg s

cost. di Planck   6,6260755^.10 erg s  6,6260755^.10 J s

massa elettrone 9,1093897^.10^{-28 g -31 kg}

massa protone  1,6726231^.10^{-24 g}

accelerazione di gravità  9,80665 ^.10 cm s 9,80665 m s

cost. di Stefan Boltzman  5,6705085 ^.10 erg cm °K s J m °K s

cost. di Wien 2,897755 ^.10^{-1 cm °K  2,897755 -3 m °K}

1 joule = 10 erg = 0,23900574 cal = 6,241506363 10 eV

1 N = 10 dyn = 0,10197162 kg

1 C ues

1 anno (tropico) = 31.556.926 s

1 Unità Astronomica (UA) = 1,49597870 10¹³ cm = 1,49597870 10 m = 1,49597870 10 km

1 anno luce (al) = 9,46053 10¹⁷ cm = 9,46053 10 m = 9,46053 10 km

1 parsec (pc) = 3,0856776 10¹⁸ cm = 3,261633 al

1 parsec cubico (pc cm al

1 megaparsec (Mpc) = 10 kiloparsec (kpc) = 10 parsec

1 megaparsec cubico (Mpc cm al

Massa solare (M g

Luminosità solare intrinseca (L erg/s = 3.847 10 watt (3.76 10 lumen = 3 10 candele)

Costante solare = 1,962 cal cm min erg cm s watt/m (1,34 10 lux )

Diametro solare (fotosfera) (D km = 1,392 10 m = 1,392 10 cm

Raggio solare (fotosfera) (R km = 6,96 10⁸ m = 6,96 10 cm

Superficie solare (fotosfera) = 6,087 10 km m = 6,087 10 cm

Potenza unitaria solare = 6.34 10 erg cm s watt/m nit)

Temperatura solare efficace (di corpo nero) T = 5778 °K

Emissione ottica del sole = 40% (tra 0,39m e 0,72m

Magnitudine solare assoluta = visuale 4,82 - bolometrica 4,75

Magnitudine solare apparente = visuale -26,75 / bolometrica -26,82

Luminosità corrispondente a M_V = 0 (fuori atm.) lumen = 2,54 10 candele

Luminosità corrispondente. a M_bol = 0 (fuori atm.) erg/s

Luminosità corrispondente. a m_V = 0 (fuori atm.) lumen/m (lux)

Luminosità corrispondente. a m_bol = 0 (fuori atm.) erg/(s cm