|
|
| |
PROGRAMMAZIONE 2
Appunti del Corso
(L. Lesmo - febbraio 2001)
PARTE TERZA
Gli alberi
INDICE
(al 19 febbraio 2001)
Indice dei Capitoli
Gli alberi 3
Strutture Dati Astratte 3
Alberi Generali 4
3.3 Memorizzazione di alberi generali: array di puntatori 5
Alberi Binari 11
3.5 Un esempio: altezza di un nodo 13
3.6 Alberi generali rappresentati mediante alberi binari 15
3.7 Lettura di un albero da file 18
Indice delle Procedure e dei Programmi
Proc. 1 - Lettura in preordine di un albero memorizzato come array di puntatori ... 8
Proc. 2 - Lettura in preordine di un albero binario ................ 12
Proc. 3 - Valutazione di un'espressione aritmetica rappresentata come albero binario . 13
Proc. 4 - Altezza di un nodo in un albero binario (versione 1) ........... 14
Proc. 5 - Altezza di un nodo in un albero binario (versione 2) ........... 14
Proc. 6 - Altezza di un nodo in un albero generale memorizzato come array di puntatori 15
Proc. 7 - Altezza di un nodo in un albero generale memorizzato come albero binario . 18
Programma 1 - Lettura di un albero da un file ...... ............ 21
Indice dei riferimenti tematici
Lo heap .......... ..... ...... 6
I tipi enumerati .............................. 20
Gli alberi
3.1 Strutture Dati Astratte
Il concetto di Struttura Dati Astratta è tra quelli fondamentali dell'informatica. L'idea è quella che è possibile definire in modo Astratto la struttura, e cioè senza specificare come essa è realizzata nell'implementazione. Sulla base di tale definizione sarà poi possibile individuare alcune operazioni che hanno senso sulla struttura astratta[1]. Date queste operazioni (e quindi il loro effetto previsto sulla struttura, cioè quella che viene detta la loro semantica, cioè il loro significato) sarà poi necessario scrivere un algoritmo che ne permetta la realizzazione. A questo punto si può cominciare a pensare alla realizzazione pratica: si dovrà scegliere un particolare linguaggio di programmazione (Pascal, C, ecc.); poi, si dovrà scegliere tra le particolari strutture dati concrete che il linguaggio mette a disposizione quella che sembra più adatta per la realizzazione dell'algoritmo; infine, si potrà passare a scrivere il programma, e cioè a tradurre l'algoritmo nel linguaggio scelto.
E' abbastanza ovvio che questa è una visione ipotetica: nella maggior parte dei casi, la scelta del linguaggio non è permessa: voi dovrete comunque realizzare gli algoritmi in Pascal, e, nella maggior parte degli ambienti industriali il linguaggio in cui realizzare il programma è fissato a priori. Ciononostante, la successione non cambia; semplicemente, si salta un passaggio:
Definisci le operazioni sulla struttura
Inventa gli algoritmi per effettuare (in modo astratto) tali operazioni
[Scegli il linguaggio: passo spesso 'saltato']
Scegli la struttura dati concreta
Scrivi i programmi
Poiché quanto detto sembra un pò generico, si può osservare che, nei capitoli precedenti, abbiamo già utilizzato delle Strutture Dati di questo tipo. Nel primo capitolo, la Struttura Dati Astratta Sequenza è stata prima realizzata con i vettori e poi con le liste. Per le Sequenze, abbiamo visto che hanno senso operazioni come
Ricerca di un elemento
Cancellazione di un elemento
Inserimento di un nuovo elemento
Modifica di un elemento
Ordinamento della sequenza
In realtà, per motivi espositivi, io mi sono concentrato su un'unica operazione: l'ordinamento (che è anche la più difficile). Una volta fatto questo (Passo 1), abbiamo cominciato a pensare ai metodi (algoritmi) possibili per realizzare l'operazione ed abbiamo 'inventato' (si fa per dire) il Selection Sort (Passo 2). Abbiamo poi ovviamente saltato il Passo 3 (il linguaggio è, per forza, Pascal) e siamo passati al passo 4. Qui, abbiamo scelto i vettori come struttura dati concreta (Tipo Array in Pascal) e, finalmente, abbiamo potuto scrivere il programma (Passo 5).
A questo punto, sono tornato indietro, e cioè al passo 2, cercando di vedere se non era possibile trovare dei metodi più efficienti per effettuare la stessa operazione. E' importante notare che non siamo tornati al passo 1! L'operazione scelta al passo 1 (l'ordinamento) è esattamente la stessa! Ma il risultato del Passo 2 è cambiato: abbiamo trovato il Merge Sort, e abbiamo visto che è migliore del Selection Sort (in termini di tempo di esecuzione). Avendo rifatto il Passo 2, dobbiamo rifare anche i passi successivi: il Passo 3 (uso di Pascal) è sempre lo stesso. Il Passo 4 (scelta della struttura dati concreta) ha portato casualmente alla scelta della stessa struttura dati, e cioè i vettori (in realtà, per noi, la scelta era obbligata, visto che le liste non le conoscevamo ancora). E infine, il passo 5, cioè la scrittura del programma Merge Sort. Notate che lo stesso algoritmo, con la stessa struttura dati concreta, può comunque portare a programmi diversi, come abbiamo visto con le varie realizzazioni di Merge Sort sui vettori[2].
3.2 Alberi generali
Quello che si vuole fare ora è di applicare la stessa metodologia (successione di passi) ad un struttura dati astratta un pò più complicata delle sequenze: gli alberi. La prima cosa da fare è di definire tale struttura; questo, nel caso delle sequenze, non era stato fatto: l'idea di sequenza è sufficientemente intuitiva. Nel caso degli alberi, invece, una definizione è necessaria.
Vi sono molti modi per definire gli alberi. Noi ne vedremo due. La prima è molto elegante, ma un pò difficile da comprendere se non si ha dimestichezza con definizioni ricorsive:
Un albero è un insieme di nodi tale che vi è un nodo speciale detto radice e tutti gli altri nodi sono partizionati in modo tale che ogni elemento della partizione è a sua volta un albero.
Un insieme vuoto di nodi è un albero
Gli insiemi che costituiscono la partizione dell'albero vengono detti sottoalberi dell'albero dato.
Questa definizione induce una gerarchia: la radice dell'albero è al livello più alto della gerarchia; le radici dei suoi sottoalberi sono al livello gerarchico immediatamente inferiore, e così via, ricorsivamente. Possiamo cioè definire il livello di un nodo nel modo seguente:
La radice dell'albero è a livello 0.
Se un nodo N è la radice di un sottoalbero di un albero la cui radice ha livello L, allora N ha livello L+1.
Esempio:
A1 =
A1 è un albero se uno dei suoi nodi è 'speciale' (la radice) e gli altri sono partizionati in sottoalberi. Ad esempio:
A1 = <n2, , , , , }>
Qui abbiamo che la radice di A1 è n2, e che A1 ha cinque sottoalberi. Naturalmente, è necessario verificare che essi siano davvero, a loro volta, degli alberi. Per , , e non ci sono problemi: l'unico nodo dell'insieme è la radice, ed essa non ha sottoalberi. Per dobbiamo ripetere (ricorsivamente) quanto già fatto per A1. Se n3 è il nodo speciale (la radice) e gli altri due nodi sono partizionati in sottoinsiemi separati, abbiamo:
<n3, , }>
Che è necessariamente un albero, per quanto detto sopra degli insiemi di un elemento.
Come ho detto sopra, questa definizione non è molto intuitiva. Vediamone un'altra:
Un albero è una coppia <N, R>, il cui primo elemento (N) è un insieme di nodi e il cui secondo elemento è una relazione binaria R NxN, tale che:
Esiste un nodo (chiamiamolo NR) che non compare come secondo elemento nella relazione R.
Tutti i nodi diversi da NR compaiono esattamente una volta come secondo elemento di R.
NR, nella definizione sopra, è la radice dell'albero, che avevamo già trovato nella prima definizione. Un esempio:
A1 = <N=,
R=>
A1 è un albero, la cui radice è n2.
Si deve notare che, come nella prima definizione, anche qui si ottiene una gerarchia (e la corrispondente nozione di livello). Infatti, se nx è la radice (a livello 0), tutti i nodi ny tali che <nx,ny> R si trovano a livello 1 (esiste cioè una connessione 'diretta' tra la radice e tali nodi). Più in generale, se un nodo nz è a livello L, allora tutti i nodi nw tali che <nz,nw> R sono a livello L+1.
Una rappresentazione grafica, più leggibile, è la seguente:
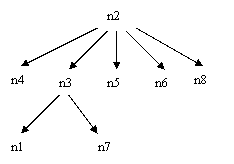
Fig.1 - Rappresentazione grafica di un albero
Si deve però osservare che mentre le prime due forme in cui l'albero è stato presentato "sono alberi", secondo le definizioni, la terza è solo "un disegno di un albero", utile per noi, ma che può corrispondere sia alla prima che alla seconda definizione, indifferentemente. Rimane comunque il fatto, fondamentale, che tutte e tre le forme si riferiscono allo stesso albero.
In tutti i casi precedenti ci siamo, comunque, riferiti ad una nozione astratta di albero (sia in modo formale, come nei primi due casi, sia in modo grafico, come nel terzo). Si è, cioè, parlato di una Struttura Dati Astratta (come era stato richiesto all'inizio). Abbiamo quindi effettuato il Passo 1. Cosa succede ora per il Passo 2? Possiamo pensare a 'ragionevoli' operazioni che si possono fare sugli alberi. Ad esempio, dato un nodo, elencare tutti i suoi figli. O, dato un nodo, elencare tutti i suoi discendenti (se il nodo dato è la radice, avremo un elenco di tutti i nodi dell'albero). Oppure, si può pensare di modificare l'albero: si possono aggiungere o eliminare dei nodi, e così via. Poiché le operazioni possibili sono tante, anziché elencarle tutte ora, possiamo immaginare di avere un elenco (magari parziale, come quello che ho fatto sopra) e cominciare a ragionare verso le strutture dati concrete.
Come si era visto nel caso delle sequenze, possono esserci diverse alternative. In quel caso, la struttura dati astratta Sequenza era stata realizzata con due strutture dati concrete (in alternativa): i Vettori e le Liste. La stessa cosa dobbiamo ora fare per gli alberi, ragionando sugli alberi, anzichè sulle sequenze.
3.3 Memorizzazione di alberi generali: array di puntatori
La prima cosa che si può osservare è che le frecce usate nella rappresentazione grafica dell'albero (che, si noti, corrispondono esattamente alle coppie che compongono la relazione R, nella seconda definizione data), assomigliano tanto a dei puntatori. Una prima soluzione, che salta subito agli occhi, è dunque la seguente: Realizziamo i nodi come record (come gli elementi di una lista per implementare una sequenza) e inseriamo, all'interno di essi dei puntatori ai figli. Sorge però un problema: visto che i puntatori sono più d'uno (ogni nodo può avere tanti figli), non possiamo usare un puntatore 'semplice', come per le sequenze. Dobbiamo perciò usare (dentro il record del nodo, per la parte relativa ai puntatori), una struttura dati complessa. Come abbiamo già visto, poichè gli elementi di questa struttura dati sono tutti dello stesso tipo (e cioè puntatori a nodi), possiamo considerarli come una sequenza di puntatori, e, come abbiamo visto, possiamo realizzarli o tramite un vettore (di puntatori) o tramite una lista (in cui la parte 'dato' è costituita da puntatori). Vediamo cosa succede adottando la prima soluzione.
Converrebbe ora riguardare la sezione relativa ai vantaggi e svantaggi di vettori e liste per la realizzazione delle sequenze. Lo svantaggio principale dei vettori è che (almeno in Pascal) è necessario dichiarare a priori (una volta per tutte) la dimensione del vettore. Come salta subito all'occhio, questo è un problema: nella definizione generale di albero non è posto alcun limite sul numero dei figli. Se però noi dichiariamo, ad esempio, che il nostro vettore di puntatori (ce ne è uno, ovviamente, per ciascun nodo) è di 100 elementi, allora non sarà possibile memorizzare un albero in cui un nodo abbia più di 100 figli. L'altro svantaggio (un pò meno grave) è relativo allo spreco di spazio: se io so che un nodo dell'albero ha 100 figli, e i suoi 100 figli hanno, in media 2 figli, i quali, a loro volta, non hanno figli, dovremo riservare spazio per:
100 puntatori per la radice
100*100 = 10.000 puntatori per i 100 figli
100*200 = 20.000 puntatori per i 200 nipoti (2 nipoti per ciascun figlio)
di questi 30.100 puntatori saranno usati solo 300 (100 dalla radice ai figli, 200 dai figli ai nipoti). Davvero uno spreco notevole!
Ciononostante, visto che questa è la soluzione più intuitiva (e in alcuni casi reali è anche possibile che il numero di figli abbia un range limitato), vediamo come questa si può realizzare. Innanzitutto, la dichiarazione Pascal delle strutture dati 'concrete' (supponiamo, nell'esempio, di aver stabilito un numero massimo di 10 figli).
const maxDaughters = 10;
type TreeNodePunt = ^TreeNode;
TreeNode = record
NodeData: TipoDato;
Daughters: array [1..MaxDaughters] of TreeNodePunt
end;
dove TipoDato è un qualsiasi tipo che descriva i dati presenti nel nodo dell'albero (ad esempio una stringa che ne costuisca l'etichetta, o un intero).
Con una memorizzazione di questo tipo, l'albero dell'esempio precedente apparirebbe come nella figura che segue (ricordiamo, si veda quanto detto per le liste, che ogni 'rettangolo' che compare nella figura rappresenta un nodo si riferisce a "un pò di memoria" riservata nello heap).
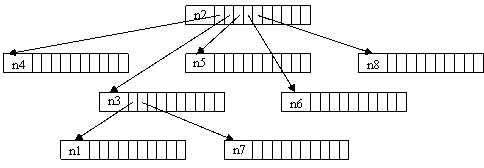
Fig.2 - Rappresentazione di un albero mediante array di puntatori
Notate che l'albero non è così ben allineato 'per livelli', come nella figura precedente. Questo l'ho fatto per una questione di spazio sulla pagina, ma è, naturalmente, irrilevante: il livello è specificato dalle relazioni tra i nodi (e quindi, nell'implementazione, dai puntatori) e non da come è fatto il disegno. Ricordate anche che i record che realizzano i nodi dell'albero sono memorizzati nello Heap, e quindi la loro posizione fisica è del tutto casuale e, di conseguenza, indipendente dalla struttura dell'albero. E' forse il caso, qui, di ricordare cos'è lo heap.
Lo heap
Sebbene la memoria centrale venga utilizzata per svariate funzioni, a noi, in questo corso, ne interessano tre:
una parte della memoria è riservata per i programmi in esecuzione. Essa includerà la codifica in linguaggio macchina del programma principale e di tutte le procedure utilizzate, oltre che lo spazio dati del programma principale. Nel corso dell'esecuzione di un programma, lo spazio occupato è fisso: le istruzioni del programma principale e delle procedure sono sempre le stesse, così come le variabili (semplici o array) definite nel main.
la seconda parte contiene lo stack. Essa ha dimensione variabile; infatti, nel corso dell'esecuzione del programma, ogni volta che viene richiamata una procedura viene allocato un blocco (frame di attivazione) sullo stack e quando la procedura termina il blocco viene liberato (e quindi lo spazio utilizzato sullo stack diminuisce). Ricordate che questo avviene per qualsiasi procedura, non solo per quelle ricorsive. Dentro ogni blocco dello stack vi sono i parametri della procedura, l'indirizzo di ritorno e le variabili locali. Notate che, mentre per ogni variabile del main è allocato un unico spazio, per quelle delle procedure c'è uno spazio diverso ad ogni chiamata, come si vedrà meglio nel seguito di questo paragrafo.
La terza parte è lo heap. Heap, in inglese vuol dire 'mucchio'. Il termine vuole dare l'idea di un insieme di celle non strutturate, cioè senza alcuna organizzazione prefissata. Dentro lo heap ci vanno i dati dinamici, e cioè i record, che possono essere 'creati' (mediante la new) e 'eliminati' (mediante la dispose) nel corso dell'esecuzione di un programma. La differenza fondamentale rispetto allo stack è che la gestione dello stack è rigida (metti in cima e togli dalla cima; infatti è una pila), e regolata dal processore (un programma non può 'decidere' se allocare o no un blocco all'atto della chiamata di una procedura), mentre la gestione dello stack è libera: è il programma che decide se e quante new eseguire e se fare o meno delle dispose.
Vi sono molti modi per gestire lo heap, che dipendono dalla macchina. In ogni caso, i programmi di gestione dello heap devono poter effettuare le operazioni seguenti:
Quando viene richiamata la new, essi devono determinare la dimensione del record che deve essere creato, in modo da sapere quanto spazio libero è necessario (e questo si determina in base alla dichiarazione del tipo). Devono cercare se nello heap c'è una sequenza di celle libere adiacenti grande a sufficienza per contenere il record. Devono 'segnalare' che queste celle sono ora occupate. Devono restituire al programma chiamante l'indirizzo delle prima di queste celle.
Quando viene chiamata la dispose, devono mettere le celle prima occupate dal record di cui si fa la dispose nello spazio libero, in modo che esso sia disponibile per successive new.
Queste operazioni sono possibili, ad esempio, mantenendo nello heap una 'lista' di spazi vuoti. All'atto della new si perrcorrerà la lista fino a trovare uno spazio vuoto grande a sufficienza e si riserverà lo spazio (parte di esso o tutto) per il programma chiamante. All'atto della dispose lo spazio liberato sarà rimesso nella lista degli spazi vuoti.
Possiamo quindi passare a vedere qualche operazione che si può effettuare sugli alberi. La cosa più naturale è la 'lettura' dell'albero. Notate che il termine lettura si usa di norma per indicare una elencazione dei nodi, e non per riferirsi all'introduzione dell'albero (input) da tastiera o da file. Se si osserva l'albero disegnato in precedenza, si può notare che vi sono due metodi principali per percorrere l'albero: o si scende per livelli, o si scende fino in fondo su uno dei cammini (dalla radice alla foglia più a sinistra) e poi si risale e si ridiscende per prendere la foglia successiva, e così via (questo può, ovviamente, essere fatto partendo dalla foglia più a destra, non cambia molto). Abbiamo così due metodi principali per percorrere un albero:
Percorrimento in ampiezza
In questo caso (lettura per livelli), si otterrà:
Livello 0 (radice): n2
Livello 1: n4, n3, n5, n6, n8
Livello 2: n1, n7
Per cui, la sequenza completa è: n2, n4, n3, n5, n6, n8, n1, n7
Si noti, comunque, che i figli di un nodo non si intendono ordinati tra loro, e che quindi il loro ordine è del tutto casuale (e non significativo).
Percorrimento in profondità
In questo caso, si otterrà:
Si parte dalla radice (n2)
Si scende sul primo figlio di n2 (n4)
Poiché n4 non ha figli si risale (n2)
Si scende sul figlio successivo di n2 (n3)
Si scende sul primo figlio di n3 (n1)
Poiché n1 non ha figli si risale (n3)
Si scende sul figlio successivo di n3 (n7)
Poiché n7 non ha figli si risale (n3)
Poiché tutti i figli di n3 sono stati esaminati, si risale (n2)
Si scende sul figlio successivo di n2 (n5)
Poiché n5 non ha figli si risale (n2)
Si scende sul figlio successivo di n2 (n6)
Poiché n6 non ha figli si risale (n2)
Si scende sul figlio successivo di n2 (n8)
Poiché n8 non ha figli si risale (n2)
Poiché tutti i figli di n2 sono stati esaminati, si risale (fine)
Sebbene questo metodo sembri molto più complicato del precedente, è in alcuni casi, di più semplice implementazione, oltre ad essere più efficiente sotto certi aspetti.
Deve essere osservato che, se si vuole usare questo tipo di percorrimento per stampare i nodi di un albero, rimangono aperte alcune possibilità di scelta. Infatti, a differenza del percorrimento in ampiezza, qui si passa sullo stesso nodo più volte. Ad esempio, si passa da n3 tre volte e da n2 ben sei volte. In teoria, la stampa dell'etichetta del nodo può essere effettuata una qualsiasi di queste volte, ma è evidente che ci sono almeno due passaggi speciali: la prima volta che si arriva ad un nodo e l'ultima volta che si passa dal nodo. Ed, in effetti, questi sono i due modi principali per elencare i nodi: nel primo caso, si parla di lettura in preordine, nel secondo caso di lettura in postordine. Nel primo caso si otterrà quindi il seguente elenco:
n2, n4, n3, n1, n7, n5, n6, n8
Mentre con la lettura in postordine otterremo:
n4, n1, n7, n3, n5, n6, n8, n2
Possiamo ora, finalmente, passare a vedere una prima procedura che opera sugli alberi. Quella che segue è la procedura per la lettura, e stampa, di un albero in preordine. La procedura utilizza ambedue le forme di 'ripetizione' viste fino ad ora: l'iterazione e la ricorsione. L'iterazione (un ciclo while) viene usata per esaminare tutti i figli di un nodo, e la ricorsione per scendere di livello.
procedure preorder (root: TreeNodePunt);
var i: integer;
begin
if root <> NIL
then
begin
writeln (root^.NodeData);
i := 1;
while (i <= maxDaughters) and (root^.maxDaughters[i] <> NIL) do
begin
preorder (root^.Daughters[i]);
i := i+1
end
end
end;
Proc.1 - Lettura in preordine di un albero memorizzato come array di puntatori
Per comprendere bene come questo programma funziona, e inoltre per ricordare i concetti principali dei meccanismi ricorsivi, può essere utile simulare l'esecuzione del programma su una (ideale) macchina a stack. La chiamata iniziale avverrà da un programma esterno (supponiamo sia il programma principale) che quindi includerà (tra altre) le seguenti istruzioni:
program esempioalbero ()
var radice: TreeNodePunt;
begin
.
leggiAlbero (radice);
.
preorder (radice);
.
end.
Supponiamo dunque che all'atto della chiamata di preorder, l'albero sia già stato letto e memorizzato nella forma che abbiamo visto sopra.
Nel momento in cui viene eseguita la chiamata a preorder, un nuovo blocco viene allocato sullo stack. Questo nuovo blocco (come tutti i blocchi associati alla procedura preorder) includerà tre elementi:
Il valore del parametro di input
L'indirizzo di ritorno
Una cella per la variabile locale i.
Disegnando lo stack dal basso verso l'alto, esso apparirà quindi nel seguente modo:

In cui, IndHeap(n2) è l'indirizzo (nello Heap) della cella in cui inizia il record che contiene il nodo n2, a è l'indirizzo (nello spazio istruzioni del programma principale) della istruzione che segue immediatamente il richiamo alle preorder, e la cella associata alla variabile i non ha ancora nessun valore.
A questo punto, inizia l'esecuzione del body della procedura. Poiché root non è NIL, viene eseguita la writeln. L'argomento (root) permette di identificare la posizione del nodo nello heap e la definizione di tipo permette di stabilire dove si trova nel record il campo cercato (nel nostro caso all'inizio) e di che tipo è tale campo (il dato da stampare). La writeln può quindi effettuare la stampa. Poi viene inizializzata la variabile i. Questo vuol dire scrivere nello stack, nella cella associata alla variabile i, il valore 1. Finalmente si entra nel while. Le condizioni sono verificate; infatti i vale 1 e, sempre grazie al valore di root (vedi stack) è possibile trovare il record relativo al nodo n2, e, da esso, prelevare il primo elemento (i vale sempre 1) dell'array di puntatori (che sta dentro il record) Daughters. Poiché Daughters(1) è il puntatore al nodo (nello Heap) n4, esso non è NIL e quindi si esegue il body della while. Nel body c'è subito la chiamata ricorsiva, che produce l'introduzione (sullo stack) di un nuovo blocco. Lo stack sarà dunque come segue:
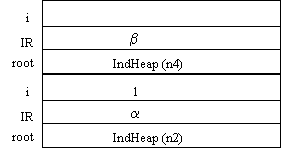
Nel nuovo blocco, la variabile root contiene l'indirizzo del record relativo al nodo n4, e l'indirizzo di ritorno è diverso dal precedente, perché quando questa esecuzione della procedura preorder sarà terminata, bisognerà tornare alla stessa procedura preorder, all'interno della quale si trovava la chiamata, e non al main. Quindi b corrisponderà all'indirizzo dell'istruzione i:=i+1, e cioè l'istruzione successiva alla chiamata ricorsiva. E' essenziale osservare che adesso, nello stack, ci sono due diverse i: quella della prima chiamata (relativa ai figli di n2, che 'ricorda' la posizione attuale: sul primo figlio, cioè n4) e quella della chiamata ricorsiva (relativa ai figli di n4, non ancora inizializzata).
Ora inizia l'esecuzione della preorder chiamata ricorsivamente. Root non è NIL, il dato (n4) viene stampato, i viene inizializzata a 1, e si verifica la condizione della while. Tale condizione non è soddisfatta! Infatti root^.Daughters[i] è NIL, poiché (anche se i vale 1) n4 non ha figli, e quindi anche il suo primo figlio è NIL. Il body della while non viene dunque eseguito nemmeno una volta e si esce dalla procedura. Si noti comunque, che l'esecuzione ha avuto un effetto, poiché n4 è stato stampato. Uscendo dalla procedura il blocco in cima allo stack viene disallocato, e quindi lo stack rimane come si vede sotto.
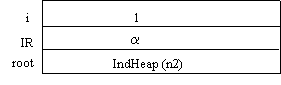
Poiché l'indirizzo di ritorno che compariva nel blocco superiore era b, la prossima istruzione da eseguire è l'incremento di i, che quindi assumerà ora il valore 2. Terminata quindi l'esecuzione del body della while, si verificano nuovamente le condizioni. Esse sono di nuovo verificate, poiché n2 ha anche un secondo figlio; quindi si esegue nuovamente il body, e lo stack diventa:
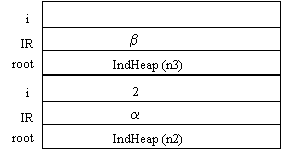
Si noti che:
L'indirizzo di ritorno è sempre b. Infatti, l'istruzione da eseguire dopo terminata l'esecuzione è sempre la i:=i+1 della procedura chiamante.
root contiene ora l'indirizzo del secondo figlio di n2, e cioè n3
Non c'è nessuna traccia sullo stack del fatto che sia già stato analizzato il sottoalbero di radice n4, eccetto per il fatto che il valore di i nel blocco in basso vale 2 e non 1! Questo però ci dice solo come continuare dopo, e non cosa è stato fatto prima: n4 poteva non avere figli (come nel nostro caso) o essere la radice di un sottoalbero molto complesso, ma lo stato in cui ci troviamo ora sarebbe esattamente lo stesso!
Non ripeto ora passo passo cosa succede: dovrebbe essere chiaro che, poiché n3 ha dei figli, la while viene eseguita. Questo comporta l'esecuzione della chiamata ricorsiva e l'aggiunta di un blocco sullo stack. La cosa più importante da osservare è che ora ci sono nello stack tre versioni della variabile i:
La prima (più in basso) ci dice che stiamo lavorando sul secondo figlio di n2 (e cioè n3).
La seconda (intermedia) ci dice che stiamo lavorando sul primo figlio di n3 (e cioè n1).
La terza (più in alto) ci dice che non abbiamo ancora cominciato a esaminare i figli di n1.
Non è un caso che siamo attualmente posizionati su un nodo al terzo livello della gerarchia (n1) e che ci siano tre blocchi sullo stack: per ciascun livello, infatti dobbiamo ricordarci a che punto siamo arrivati!

Ora, si verificherà (dopo averlo stampato) che il nodo n1 non ha figli, e quindi si risale sull'albero, il che corrisponde a togliere un blocco dallo stack, e poi si ridiscenderà si n7 (aggiunta di un blocco) e così via.
3.4 Alberi binari
In un albero binario, ogni nodo ha zero, uno, o due figli. Però, gli alberi binari non sono un caso particolare degli alberi generali che abbiamo appena visto (in cui si abbia MaxDaughters=2); infatti, essi non rispettano le definizioni precedenti. Il motivo è che negli alberi binari vengono distinti i due possibili figli in figli sinistri e figli destri. In altre parole, l'ordine dei figli è, nel caso degli alberi binari, di importanza fondamentale! Scambiare il figlio sinistro e il figlio destro in un albero binario produce due alberi diversi. Al contrario, scambiare il primo e il secondo figlio di un nodo in un albero generale non ha alcun effetto: l'albero risultante è lo stesso albero dell'albero originale (l'ordine dei figli non ha importanza). Non solo, ma anche avendo un unico figlio, è diverso il caso in cui tale figlio sia figlio sinistro dal caso in cui esso sia figlio destro.
Non c'è molto da dire sulle modalità di rappresentazione degli alberi binari, poiché la soluzione è praticamente immediata (e unica, visto che non presenta particolari inconvenienti):
type BinaryNodePointer = ^BinaryNode;
BinaryNode = record
NodeData: TreeData;
LeftD, RightD: BinaryNodePointer;
end;
Come si vede, si tratta di record che includono un campo per i dati (nome o etichetta del nodo) e due distinti puntatori: il primo al figlio sinistro (l'ho chiamato LeftD) e il secondo al figlio destro (RightD).
Possiamo subito vedere la procedura di lettura in preordine di un albero binario, che non è altro che una semplificazione di quella già vista per gli alberi generali.
L'unica differenza è che qui, anziché avere un ciclo while, con la corrispondente necessità di inizializzare e incrementare la variabile i, si hanno solamente due richiami ricorsivi in sequenza: il primo per il sottoalbero che ha come radice il figlio sinistro, il secondo per il sottoalbero che ha come radice il figlio destro. E' chiaro che qui il ciclo non serve: si sa che i puntatori ai figli sono esattamente due (anche se uno o tutti e due potrebbero essere NIL)!
procedure BinPreorder (root: BinaryNodePointer);
begin
if root <> NIL
then
begin
writeln (root^.NodeData);
BinPreorder (root^.LeftD);
BinPreorder (root^.RightD)
end
end;
Proc.2 - Lettura in preordine di un albero binario
Gli alberi binari sono molto importanti, perché, pur avendo una struttura molto semplice, permettono di memorizzare (con una tecnica un pò particolare) anche alberi generali. Prima, però, di vedere tale tecnica, facciamo un esempio di uso di alberi binari. In particolare, gli alberi binari possono essere utilizzati per memorizzare delle espressioni aritmetiche. Vediamo quindi come questo può essere realizzato, ed una procedura per valutare l'espressione.
Nell'espressione, assumiamo che tutti gli operatori siano binari e che gli unici operatori permessi siano +, -, *, /. Nella scrittura dell'espressione, possiamo inserire tutte le parentesi, che ci consentono di ricavare in modo immediato la struttura interna dell'espressione. Ad esempio:
((3+7) - (18 * (10/5)))
In questa espressione compare un operatore principale (che è quello relativo alle parentesi più esterne, nel nostro caso -) che può avere come argomenti o dei valori interi o delle espressioni aritmetiche. Nel nostro caso, ambedue gli argomenti dell'operatore principale sono a loro volta delle espressioni: (3+7) e (18*(10/5)). Ciascun operatore può essere rappresentato come un nodo di un albero binario, i cui argomenti sono i sottoalberi sinistro e destro. Ad esempio, nel nostro caso:
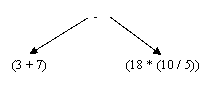
Naturalmente, poiché la definizione è ricorsiva, anche i sottoalberi verranno rappresentati nello stesso modo, ottenendo così alla fine:
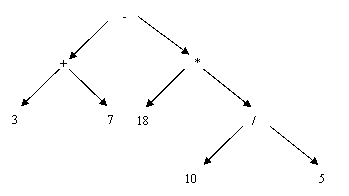
Si osservi che le parentesi tonde non compaiono più: esse infatti servono solo per rendere espliciti, nella rappresentazione lineare 'standard' dell'espressione i livelli di annidamento delle sottoespressioni; ma questo, nell'albero, è già dato esplicitamente nella struttura dell'albero stesso.
Possiamo ora pensare alla struttura (tipo Pascal) dei nodi dell'albero. Innanzitutto, poiché le foglie dell'albero hanno associati dei dati interi, mentre i nodi intermedi si riferiscono a dati di tipo char, non sarà possibile memorizzare tali informazioni nello stesso campo del record. Di conseguenza, dovremo avere due campi 'dati': il primo sarà di tipo integer e verrà usato quando il record contiene i dati di una foglia. Il secondo sarà di tipo char e verrà usato, nei nodi intermedi, per memorizzare l'operazione. Ora però sorge un problema: come fare a sapere di che tipo di nodo si tratta? E', ovviamente, possibile verificare sempre se un nodo non ha figli (nel qual caso dovrà necessariamente contenere un valore, e non un operatore), ma è più semplice utilizzare lo stesso campo usato per l'operazione come indicatore di tipo di nodo; ad esempio, possiamo porre in tale campo il valore 'v', se il nodo contiene un valore intero (e cioè si tratta di una foglia). A questo punto, possiamo dare la definizione di tipo:
type AritmPointer = ^AritmNode;
Nlabel: char;
Nvalue: integer;
LeftD, RightD: AritmPointer
end;
Ora, scrivere la procedura per la valutazione dell'espressione è proprio facile: per ogni nodo (partendo dalla radice), si verifica il 'tipo'; se si tratta di un'operazione, la si esegue; se si tratta di un valore (una foglia) si prende il valore. Ovviamente, per eseguire un'operazione sarà necessario conoscere il valore dei suoi operandi; ma questi si ottengono valutando l'espressione associata al sottoalbero, e cioè con due chiamate ricorsive (una per il primo operando, sottoalbero sinistro, una per il secondo operando, sottoalbero destro) alla stessa funzione (che chiamerò aritmEval:
function aritmEval (root: AritmPointer): integer;
begin
case root^.Nlabel of
'+': aritmEval := aritmEval (root^.LeftD) + aritmEval (root^.Rightd)
'-': aritmEval := aritmEval (root^.LeftD) - aritmEval (root^.Rightd)
'*': aritmEval := aritmEval (root^.LeftD) * aritmEval (root^.Rightd)
'/': aritmEval := aritmEval (root^.LeftD) / aritmEval (root^.Rightd)
'v': aritmEval := root^.Nvalue
end;
Proc.3 - Valutazione di un'espressione aritmetica rappresentata come albero binario
Si osservi solo che, per i nodi intermedi, il campo Nvalue non è utilizzato. Volendo, è possibile (con semplici modifiche alla procedura) memorizzare in esso i risultati (parziali) del calcolo delle sottoespressioni.
3.5 Un esempio: altezza di un nodo
Un utile esercizio, che ci permette di confrontare le operazioni sugli alberi binari con quelle sugli alberi generali, è quello del calcolo dell'altezza di un nodo. Definiamo per altezza del nodo n, la massima distanza di n da una foglia. Più precisamente:
Se n è una foglia, allora altezza(n)=0
Se n non è una foglia, allora altezza(n)=Max(altezza dei suoi figli)+1
Cominciamo a vedere come questa definizione può essere realizzata su alberi binari. La cosa più interessante della procedura che segue, è che essa ricalca esattamente la definizione data!
function height (node: BinaryNodePointer): integer;
begin
if (node^.LeftD = NIL) and (node^.RightD = NIL)
then height := 0
else if node^.LeftD = NIL
then height := height (node^.RightD) + 1
else if node^.RightD = NIL
then height := height (node^.RightD) + 1
else height := max (height (node^.LeftD),
height (node^.RightD)) + 1
end;
Proc.4 - Altezza di un nodo in un albero binario (versione 1)
L'unica differenza, rispetto alla definizione, è che, per trovare il massimo dell'altezza dei figli, si devono trattare separatamente i casi in cui uno dei due figli è NIL (cioè, manca). Un'alternativa, un pò più elegante, è la seguente:
function height2 (node: BinaryNodePointer): integer;
begin
if node = NIL
then height2 := -1
else height2 := max (height2 (node^.LeftD), height (node^.RightD)) + 1
end;
Proc.5 - Altezza di un nodo in un albero binario (versione 2)
La differenza, rispetto alla versione precedente, e che qui non si termina la ricorsione sulle foglie, ma si scende di un livello in più, andando a considerare i figli NIL (cioè assenti). La cosa interessante è che questo si applica sia alle foglie (in cui ambedue i figli sono NIL) sia ai nodi con un solo figlio (destro o sinistro). Nel caso di una foglia, noi vogliamo che la sua altezza sia 0, per cui, visto che la definizione richiede che l'altezza di un nodo sia pari all'altezza massima dei suoi figli incrementata di 1, sarà necessario che l'altezza che si ottiene da un puntatore NIL sia -1. In questo modo, per le foglie, si ha che l'altezza di ambedue i figli (NIL) è -1, il massimo è quindi -1, e il massimo incrementato di 1 è 0 (come desiderato). Nel caso in cui uno solo dei due figli sia NIL, il valore dell'altezza è determinato dall'altro figlio, per cui il valore -1 non ha alcun effetto (l'altezza di un qualunque nodo è maggiore di -1).
Per calcolare l'altezza di un nodo in un albero generale, il procedimento è sempre lo stesso, ma con una piccola estensione per tener conto che un nodo può avere da 0 a un certo massimo[3] (io userò 10) di figli. Poiché in un albero generale non si sa quanti sono i figli, è necessario un ciclo che operi sui figli (che ripeterà il body tante volte quanti sono i figli. Quindi, per spostarsi sulla successione dei figli di un nodo, si userà un procedimento iterativo (ciclo while, appunto). Per quanto riguarda la discesa sull'albero, al contrario, valgono le considerazioni che avevamo fatto per la procedura preorder e cioè che è necessario mantenere sullo stack le informazioni locali relative alle diverse chiamate. Ma c'è qualcuno che già fa questo per noi, e cioè il meccanismo di gestione delle chiamate di procedura, che inserisce un blocco sullo stack per ogni chiamata (e cioè, per ogni livello dell'albero, come desiderato). La struttura complessiva della procedura è quindi molto simile a quella che avevamo già visto per preorder.
function height3 (node: TreePointer): integer;
var tempheight: integer;
begin
if node = NIL
then height3 := -1
else
begin
tempheight := -1;
i := 1;
while (i<= MaxDaughters) and (node^.Daughters[i] <> NIL) do
begin
tempheight := max (tempheight, height3 (node^.Daughters[i]);
i := i+1
end
height3 := tempheight + 1
end
end;
Proc.6 - Altezza di un nodo in un albero rappresentato tramite array di puntatori
Penso sia utile confrontare questa versione con l'ultima versione vista per gli alberi binari. La differenza principale qui, come è ovvio, è che al posto della semplice operazione
height2 := max (height2 (node^.LeftD), height (node^.RightD)) + 1
è necessaria l'introduzione del ciclo while. Per rendersi conto meglio dell'analogia, osservate che l'operazione riportata qui sopra è equivalente a:
tempheight := -1;
tempheight := max (tempheight, height2 (node^.LeftD));
tempheight := max (tempheight, height2 (node^.RightD));
height2 := tempheight + 1
Il che è praticamente identico allo sviluppo della while del programma per alberi generali, nel caso in cui si eseguano solo due cicli. Si noti, comunque, che la seconda condizione della while (e cioè node^.Daughters[i] <> NIL) potrebbe anche essere omessa; l'unica differenza sarebbe che viene effettuata la chiamata ricorsiva su tutti i 10 puntatori, anche quelli a NIL che non corrispondono a nessun figlio. Ma visto che per essi il valore ottenuto è -1, questo non provoca problemi. Naturalmente, questo è molto inefficiente, perché bisogna effettuare una chiamata ricorsiva in più, anche per tutti i figli inesistenti (con relativa allocazione-deallocazione di un blocco sullo stack).
3.6 Alberi generali rappresentati mediante alberi binari
Dobbiamo ora ritornare al paragrafo 3.3, in cui abbiamo scelto di rappresentare gli alberi generali come array di puntatori. Allora, si era sottolineato come questa soluzione soffrisse di tutti i problemi legati alla rappresentazione di sequenze tramite vettori: limite sul numero massimo di elementi e spreco di spazio. Ora, è il caso di chiedersi se, anziché un vettore di puntatori, non sia possibile usare una lista di puntatori (esattamente come avevamo fatto nel caso delle sequenze di interi, mentre si trattava il problema dell'ordinamento).
Naturalmente, questa soluzione è possibile (i vettori possono essere sempre sostituiti da liste). Il nostro albero di esempio (vedi le figure 1 e 2) risulta, con le liste di puntatori, rappresentato come si vede nella figura che segue.
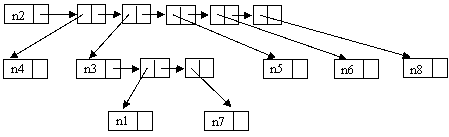
Figura 3 - Sequenza dei puntatori ai figli realizzata come lista di puntatori
Come si vede dalla figura, ci sono due tipi di puntatori: quelli che puntano a dei nodi (con l'etichetta) e quelli che puntano a 'coppie di puntatori'. Questo è naturale: i primi sono i nostri vecchi puntatori dell'albero, i secondi sono dei puntatori che ci servono a rappresentare la sequenza di (puntatori ai) figli come lista. Questo metodo di rappresentazione può essere 'dichiarato' in Pascal nel modo seguente:
Type ToNodePointer = ^TreeNode;
PointerListPointer = ^PointerNode;
TreeNode = record
NodeData: TipoDato;
FirstDaughter: PointerListPointer
end;
PointerNode = record
Daughter: ToNodePointer;
NextDaughter: PointerListPointer
end;
Si può osservare che il tipo PointerNode prevede una coppia di puntatori (anche se di tipo diverso). Il primo di essi (di tipo ToNodePointer) è in realtà un 'dato' (come gli interi del nostro esempio di sort), mentre il secondo è il vero 'puntatore al prossimo elemento'. Notate infine che il 'puntatore all'inizio della lista (dei figli)' non è memorizzato in una variabile del main o della procedura, ma dentro i record stessi (e cioè nello Heap); in particolare, nei record di tipo TreeNode.
Sebbene questa rappresentazione risolva i problemi visti per i vettori (ci sono solo tanti puntatori quanti servono e non ce n'è un numero massimo), forse si può fare meglio! Se guardate bene la figura, vedete che, per ogni nodo di tipo ToNodePointer c'è un corrispondente nodo di tipo TreeNode, e viceversa. In altre parole, c'è un accoppiamento rigido (una relazione 1 a 1) tra nodi ToNodePointer e nodi TreePointer. E inoltre, per arrivare al primo figlio di un nodo, bisogna fare un doppio passaggio: prima si deve passare per il nodo 'coppia di puntatori' e poi, da esso, si può arrivare al vero 'nodo che contiene i dati'.
Perché, allora, non fondere in un unico nodo ogni ToNodePointer con il TreeNode ad esso associato? Se facciamo questa operazione, otteniamo la seguente rappresentazione:

Figura 4 - Un albero generale rappresentato come albero binario (a parte la radice)
Beh, questa realizzazione sembra molto più semplice della precedente. Qui abbiamo che ogni nodo ha due puntatori; il primo di essi punta al primo figlio (se c'è), mentre il secondo punta al fratello successivo (se c'è). L'unico problema è quello della radice, che ha un solo puntatore; questo dipende dal fatto che la radice non può avere un 'fratello successivo'. Ma noi possiamo lo stesso mettere nel record questo puntatore (per avere un nodo fatto come tutti gli altri), anche se esso sarà sempre NIL.
A questo punto, il tipo Pascal per questa rappresentazione può essere come segue:
Type NodePointer = ^TreeNode;
TreeNode = record
NodeData: TipoDato;
FirstDaughter: NodePointer;
NextSister: NodePointer
end;
Ma questi tipi assomigliano (anzi sono esattamente uguali) a quelli che avevamo visto per gli alberi binari! Quindi, quello che abbiamo ottenuto è un albero binario! Ma a questo siamo arrivati per rappresentare un albero generale. Di conseguenza, quella che abbiamo trovato è una rappresentazione di alberi generali fatta mediante alberi binari. Ripeto, perché è importante: la struttura dati astratta è l'albero generale, mentre l'implementazione (struttura dati concreta) è quella di un albero binario.
 Per comprendere
meglio questa differenza, riprendiamo il problema di determinare l'altezza di un
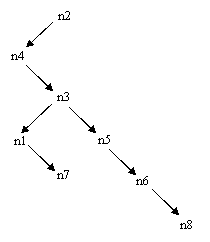
nodo. Ridisegniamo però, prima, l'albero binario di Fig.4 nel nostro solito
formato 'leggibile'.
Per comprendere
meglio questa differenza, riprendiamo il problema di determinare l'altezza di un
nodo. Ridisegniamo però, prima, l'albero binario di Fig.4 nel nostro solito
formato 'leggibile'.
Ora, qual è l'altezza della radice di quest'albero? Facile! Guardando la figura, si vede subito che l'altezza è 5! Facile, ma sbagliato. Se questo albero è solo un'implementazione diversa del nostro vecchio albero delle figure precedenti, allora l'altezza che vogliamo è quella della radice di quell'albero, e cioè 2. Il motivo dell'errore è semplice: muoversi verso il sottoalbero destro non deve far aumentare l'altezza! Infatti, ci stiamo solo spostando tra 'fratelli', che hanno tutti la stessa altezza. Proviamo allora a scrivere una procedura che ci permetta di calcolare l'altezza 'giusta' (ovviamente, possiamo far 'girare' il programma che calcola l'altezza di un nodo negli alberi binari sull'albero dell'esempio, ma in questo caso otterremo, appunto, il risultato 'sbagliato', cioè 5).
Per ottenere l'altezza di un albero generale rappresentato come albero binario, scriviamo, come al solito, una procedura iterativa in ampiezza e ricorsiva in profondità. Naturalmente, in questo caso, l'iterazione in ampiezza comporta non un ciclo su un vettore, ma un ciclo su una lista. E quindi il ciclo terminerà quando si sarà raggiunta la fine della lista (NextDaughter=NIL).
function height4 (node: TreePointer): integer;
var tempheight: integer;
begin
if node = NIL
then height4 := -1
else
begin
tempheight := -1;
nextDaughter := node^.FirstDaughter;
while nextDaughter <> NIL do
begin
tempheight := max (tempheight, height4 (nextDaughter));
nextDaughter := nextDaughter^.NextSister
end;
height4 := tempheight + 1
end
end;
Proc.7 - Altezza di un nodo di un albero generale rappresentato come albero binario
Come si può vedere, questa procedura corrisponde esattamente alla Proc.6 (Altezza di un albero rappresentato come array di puntatori). La differenza che può essere difficile da comprendere è quella relativa all'inizializzazione del ciclo while. Nel caso di Proc.6, era sufficiente porre i:=1 (che vuol dire posizionarsi sul primo figlio); qui, per posizionarsi sul primo figlio, è necessario scendere sul sottoalbero sinistro; infatti nextDaughter, che ha la funzione di variabile di ciclo, viene inizializzata a node^.FirstDaughter.
3.7 Lettura di un albero da file
In quest'ultimo paragrafo riporto un programma completo per leggere un albero da un file e stamparlo in preordine. Ricordo che sto parlando di un file solo perché i dati, se memorizzati in un file, saranno disponibili per diverse prove (i programmi raramente funzionano al primo colpo). Lo stesso input può essere anche dato, volendo, da tastiera; si riveda la discussione sui files nel primo capitolo di queste dispense.
Il primo problema da affrontare è relativo al modo in cui dare l'albero in input. Ovviamente, non possiamo usare puntatori: i puntatori non si possono leggere né stampare, visto che sono oggetti interni (indirizzi sullo heap). Ma tutte le rappresentazioni che abbiamo usato coinvolgono dei puntatori! L'unica alternativa è quella di ritornare alle nostre definizioni della struttura dati astratta 'albero'. Possiamo liberamente scegliere una qualunque delle due; io sceglierò la seconda (con alcune modifiche).
Ricordo (si veda il §3.2) che un albero può essere definito come una coppia il cui primo elemento è un insieme di nodi e il secondo è un insieme di archi. Per prima cosa, io non userò il primo elemento: in input verranno dati solo gli archi, assumendo che in questo modo i nodi siano (implicitamente) definiti. Ciascun arco verrà descritto come una coppia <genitore, figlio>.
Per una questione di semplicità, assumerò inoltre che l'albero venga costruito, un arco alla volta, partendo dalla radice. Questo vuol dire che, ogni volta che viene letto un arco, verrà aggiunto un nuovo nodo, figlio di un nodo già presente. In altre parole, non deve essere possibile introdurre un nodo intermedio nell'albero che si sta costruendo, ma vengono aggiunte solo foglie (che magari non saranno foglie alla fine, poiché ad esse potranno essere aggiunti, in seguito, dei figli). Questo perché l'aggiunta di una foglia è un'operazione molto semplice, mentre l'aggiunta di un nodo intermedio è un po' più complicata.
Questa strategia è abbastanza naturale, ma ha due conseguenze:
Non possiamo applicare la definizione di radice. Tale definizione, infatti, richiede di avere a disposizione tutti gli archi, per verificare quale nodo non compare mai come secondo elemento (cioè non è figlio di nessun altro nodo). Quando si legge un arco, invece, non si sa ancora come saranno gli altri archi che seguono.
Ogni volta che si introduce un arco, il genitore (primo elemento della coppia) deve già essere presente nell'albero.
Poiché l'albero deve crescere dall'alto verso il basso, il primo nodo da introdurre deve essere la radice. Ma noi non possiamo introdurre nodi, ma soltanto archi. Per risolvere il problema, inventiamoci un arco fittizio; diciamo che c'è un nodo (fasullo) che sta sopra la radice e identifichiamolo con un simbolo speciale (ad esempio *).
A questo punto, l'algoritmo di lettura è abbastanza semplice:
Per ogni arco:
se il primo elemento è *, allora si tratta della radice
altrimenti, cerca nell'albero costruito finora il primo elemento (il genitore) e inserisci il secondo elemento come suo figlio
Si possono però verificare alcuni errori (se i dati nel file non sono stati messi come previsto):
Può esserci più di una coppia il cui primo elemento è * (più di una radice)
Il primo elemento della coppia (diverso da *) non c'è nell'albero (si sta cercando di introdurre un figlio senza aver ancora introdotto il genitore)
Si cerca di introdurre un figlio per un genitore che ha già raggiunto il numero massimo di figli (questo è un problema della rappresentazione con array di puntatori)
Per questo motivo, sembra ragionevole introdurre un meccanismo di segnalazione degli errori: se si verifica uno di questi errori, dovrà comparire a video una scritta che descriva il tipo di errore.
Possiamo ora vedere il programma; dobbiamo però ancora decidere come sono fatti i 'dati', e cioè le etichette dell'albero. Questa volta, userò come dato un carattere (tipo char). C'è però ancora un problema: cosa succede se introduciamo due volte lo stesso carattere? Questo è un problema interessante che richiede due parole di spiegazione (il problema non dipende dal fatto che io abbia scelto un carattere, con gli interi sarebbe stato lo stesso)[4]. Spesso si tende a confondere un nodo con la sua etichetta (il dato che esso contiene). Ma le due cose sono completamente diverse! Nella definizione di albero si dice che un albero è un insieme di 'nodi', non di 'etichette di nodi' (o 'nomi di nodi'). Poiché si parla di un insieme, i nodi devono essere diversi: in un insieme non ci sono elementi uguali. Ma nulla esclude che due elementi distinti abbiano etichette (o in generale, dati) uguali. E' chiaro che un insieme di persone può anche includere due persone (diverse) con lo stesso nome. A questo punto, ci si può chiedere: ma allora come facciamo a distinguere due elementi che hanno gli stessi dati? Da un punto di vista applicativo, questo è un problema serio (non per niente sono stati inventati i codici fiscali), che non è il caso di approfondire qui. Ma nel nostro piccolo (la lettura dell'albero) si possono fare due osservazioni interessanti. Due 'nodi' con la stessa etichetta sono diversi perché sono memorizzati in due record diversi! E cioè ci saranno celle diverse nello heap che contengono lo stesso dato. Ma il fatto che i record siano diversi non vuol dire che noi siamo in grado di trovare quello giusto! Supponiamo infatti di aver introdotto due coppie <a,z> e <b,z>. Fin qui, nulla di male. Ma se ora introduciamo la coppia <z,c>, sotto quale dei due 'z' dovrà essere introdotto 'c'? Non c'è nulla da fare: non abbiamo modo per distinguerli! Ci manca un identificatore univoco (appunto, un 'codice fiscale' dei nostri nodi)! Io non mi preoccuperò di questo problema nel programma che segue. Un modo possibile per risolverlo è quello di imporre che non possano esserci due nodi con la stessa etichetta (cosicchè l'etichetta è l'identificatore univoco): questo controllo non è fatto nel programma, ma non è difficile aggiungerlo. Di conseguenza, quello che succederà nel programma nella situazione descritta sopra (inserimento di <a,z>, <b,z> e <z,c>) è che 'c' verrà inserito come figlio sotto il primo 'z' che si trova. Poiché la procedura di ricerca del genitore è sempre la stessa, ogni figlio di 'z' andrà sempre sotto lo stesso 'z'. L'altro, poverino, rimarrà per sempre senza figli!
Possiamo ora vedere il programma.
Ho assunto che ogni nodo possa avere al massimo 10 figli (maxDaughters). Per quanto riguarda gli errori, ho introdotto un tipo 'nuovo', il cosiddetto tipo enumerato.
I tipi enumerati
Come sappiamo, in Pascal ci sono tre classi di tipi: quelli semplici (es. Integer) e quelli strutturati (es. array) e i puntatori. I tipi semplici, a loro volta, si suddividono in Ordinali e Reali. Gli ordinali, infine, possono essere predefiniti (e questi sono 3: Integer, Boolean e Char), enumerati e subrange. Dirò qui due parole sui tipi enumerati.
Un tipo enumerato specifica un elenco ordinato di valori, a scelta di chi definisce il tipo. Questo viene fatto semplicemente indicando i valori voluti tra parentesi tonde:
type giorno = (lun, mar, mer, gio, ven, sab, dom);
type sesso = (mas, fem);
E' importante osservare che i valori che vengono specificati per il tipo non sono stringhe (cioè array di Char), né nomi di variabili, ma sono delle costanti come ad esempio 127 (un intero) o false (un booleano). In particolare, Pascal prevede di essere in grado di stabilire sempre il tipo, quando trova una costante in un programma, per cui se aggiungiamo alle dichiarazioni sopra:
type vacanza = (mon, mar, cam, via);
che starebbero per 'montagna', 'mare', 'campagna', 'viaggio', si verifica un errore, perché mar è una costante ambigua (è sia un giorno che una vacanza). Inoltre, il tipo è definito tramite un elenco ordinato (infatti numerali fanno parte dei tipi ordinali). In altre parole, l'ordine con cui vengono specificati i valori è rilevante. Ad esempio,
lun < mer vale true (è vero)
mentre
fem < mas vale false (è falso)
Ovviamente, come per tutti i tipi, si possono definire variabili di un tipo enumerato:
var oggi, domani: giorno;
sessoDelProprietario: sesso;
e operare su di esse in modo standard:
oggi := dom;
sessoDelProprietario := fem;
Non solo, ma grazie alla presenza di un ordinamento si possono fare cose un po' più 'singolari' (a prima vista):
for oggi := lun to ven
stampaOreLezione (oggi);
Oppure
if oggi > ven then writeln ('Finalmente!!!');
Infine, è possibile usare un tipo enumerato come indice di array:
type CoppiaOre = record
ore, minuti: integer
end;
type orario = array [lun..ven] of CoppiaOre;
Per cui sarà poi possibile riferirsi all'orario del giovedì con:
orario[gio]
Ma c'è anche qualcosa di utile che NON si può fare; in particolare, non è possibile leggere o stampare un valore di un tipo enumerato:
readln (domani); è sbagliato!
Per concludere, menzionerò l'esistenza di procedure predefinite che operano su tipi enumerati; in particolare:
succ(x), prec(x) e ord(x) (successore, predecessore e numero d'ordine)
ad esempio, se oggivale mer:
succ(oggi) gio
prec(oggi) mar
ord(oggi)
Si noti solo che i numeri d'ordine partono da 0 (non da 1) e che l'elenco non è ciclico, per cui succ(dom) non è lun, ma produce una segnalazione di errore.
Possiamo ora tornare al nostro programma. Esso comprende tre procedure:
La locate trova un nodo (data l'etichetta) nell'albero costruito fino ad ora (è quella che trova sempre lo stesso 'z', anche se ce ne sono più d'uno)
La addDaughter, dato un nodo genitore e un nodo figlio, inserisce il figlio (se il genitore non ne ha già 10)
La readTree, che fa la vera e propria lettura (usando la locate per trovare il genitore, la new per allocare lo spazio nello heap per il nuovo figlio e la addDaughter per legare il genitore al figlio).
La locate ricalca esattamente la lettura in preordine di un albero. Ho solo aggiunto la variabile booleana found, che dice quando, in un sottoalbero, è stata trovata l'etichetta cercata, per evitare l'inutile ricerca negli altri sottoalberi (questo, ovviamente, non ha senso nella preorder, poiché in quel caso tutti i sottoalberi vanno percorsi per effettuare la stampa).
La addDaughter cerca, nella array di puntatori del padre, il primo puntatore NIL e lo sostituisce con il puntatore al nuovo figlio. Se tutti i puntatori sono diversi da NIL, segnala un errore (manyDaughters).
La readTree è un ciclo while di lettura da file. Suppongo che nel file di input ogni riga corrisponda a un arco. La funzione eof(f) dà True se siamo in fondo al file (eof sta per End Of File), e quindi not eof(f) è vero se ci sono ancora righe da leggere. Le righe del file sono nella forma:
x y
in cui x è l'etichetta del genitore e y quella del figlio. Questo comporta un piccolo problema di lettura, perché lo spazio che separa x da y è un carattere come tutti gli altri. Se io faccio
readln (f, upLabel, downLabel);
la readln, che sa che upLabel e downLabel sono di tipo char, assegna 'x' a upLabel e ' ' (cioè lo spazio) a downLabel. Per evitare che questo succeda, possiamo fare due cose: o inserire i dati nella forma
xy
e cioè senza spazio (ma questo non sembra molto leggibile), oppure far leggere tre caratteri, il secondo dei quali (lo spazio) non sarà più usato. Io ho adottato la seconda soluzione, facendo leggere anche la variabile blank. A questo punto si crea il figlio (new) inserendo la nuova etichetta e mettendo a NIL tutti i puntatori. Questa è un'operazione importante, perché altrimenti i puntatori non hanno un valore e non si può controllare se sono NIL. Si controlla poi se upLabel è '*'. In questo caso si sta introducendo la radice. Questo comporta l'assegnazione alla variabile root (passata per riferimento, per cui l'assegnazione viene in realtà effettuata su una variabile del main) del nodo appena creato, dopo aver verificato che root non abbia già un valore (nel qual caso, nel file, c'è più di una radice). Se upLabel non è '*', si cerca il nodo con etichetta upLabel nell'albero (locate) e si aggiunge il nuovo figlio (addDaughter).
Le varie procedure effettuano vari controlli, fanno delle stampe intermedie che permettono di seguire quello che succede nel corso dell'esecuzione e, se necessario, impostano la variabile error. Il main richiama readTree, stampa 'Lettura terminata' e poi, se non ci sono stati errori (la variabile error ha ancora il valore originale ok) stampa in preordine l'albero letto.
program alberi;
const maxDaughters = 10;
type nodePointer = ^treeNode;
treeNode = record
nodeLabel: char;
daughters: array[1..maxDaughters] of nodePointer;
father: nodePointer
end;
errorCode = (ok, manyroots, nofather, manydaughters);
var treeroot: nodePointer; error: errorCode;
function locate (tree: nodePointer; nlabel: char): nodePointer;
var found: boolean; i: integer; temp, nextd: nodePointer;
begin
found := false;
if tree = NIL
then locate := NIL
else
begin
if tree^.nodeLabel = nlabel
then locate := tree
else
begin
locate := NIL;
i := 1;
while (i <= maxDaughters) and
(tree^.daughters[i] <> NIL) and
(not found) do
begin
temp := locate (tree^.daughters[i], nlabel);
if temp <> NIL
then
begin
found := true;
locate := temp
end
else i := i+1
end
end
end
end;
procedure addDaughter (father, daughter: nodePointer; var err: errorCode);
var i: integer; done: boolean;
begin
i:= 0;
done := false;
while (i <= maxDaughters) and (not done) do
begin
if i=maxDaughters
then
begin
writeln (father^.nodelabel, ' ha troppi figli');
err:= manydaughters;
i := i+1;
readln
end
else
begin
i := i+1;
if father^.daughters[i] = NIL
then
begin
done:= true;
father^.daughters[i] := daughter
end
end
end
end;
procedure readtree (var root: nodePointer; var error: errorCode);
var f: text; nextNode: nodePointer; upLabel, downLabel, blank: char;
i: integer;
begin
assign (f, 'treedata.dat');
reset (f);
while not eof(f) do
begin
readln (f, upLabel, blank, downLabel);
readln;
writeln ('Genitore:', upLabel, ' ; figlio: ', downLabel);
new (nextNode);
for i := 1 to maxDaughters do nextNode^.daughters[i] := NIL;
nextNode^.nodeLabel := downLabel;
if uplabel = '*'
then
if root = NIL
then
begin
nextNode^.father := NIL;
root := nextNode
end
else
begin
writeln ('Errore: più' di 1 radice');
error := manyroots;
readln
end
else
begin
nextnode^.father := locate (root, upLabel);
if nextNode^.father = NIL
then
begin
writeln ('Errore: figlio definito prima del padre');
error := nofather;
readln
end
else
begin
writeln ('locate; trovato padre di ', downLabel);
addDaughter (nextNode^.father, nextNode, error)
end
end
end
end;
procedure preorder (root: nodePointer);
var i: integer;
begin
if root <> NIL then
begin
i := 1;
writeln (root^.nodeLabel);
while (i <= maxDaughters) and (root^.Daughters[i] <> NIL) do
begin
preorder (root^.Daughters[i]);
i := i+1
end
end
end;
begin
error := ok;
readtree (treeRoot, error);
writeln ('Lettura terminata');
readln;
if error = ok then
begin
writeln ('Risultato lettura in preordine:');
preorder (treeRoot)
end;
readln
end.
Di norma per Struttura Dati Astratta si intende l'organizzazione dei dati unitamente alle operazioni fondamentali definite sui dati stessi.
Questo non è del tutto preciso. In realtà, i vari programmi di Merge Sort sono realizzazioni di 'specializzazioni' diverse dell'algoritmo fondamentale: ad un certo livello di dettaglio (astrazione) sono lo stesso algoritmo, ad un altro livello sono algoritmi differenti.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025