|
|
| |
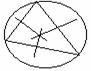
CIRCOCENTRO.
Gli assi dei lati di un triangolo passano
per uno stesso punto equidistante dai vertici (detto circocentro).
Dato il triangolo ABC vogliamo provare che gli asssi dei suoi lati passono per
uno stesso punto O=punto comune dei lati AB e BC. Allora è equidistante a tutti
i 3 lati. Cioè si ha OA= OB, ed OB= OC percui si ha che OA =OC ;da ciò
deduciamo che i tre assi del triangolo passono tutti per O
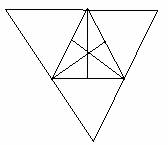
ORTOCENTRO. Le
tre altezze di un triangolo passano per uno stesso punto (detto ortocentro).
Dato il triangolo ABC, sia OPQ il triangolo ottenuto conducendo per ogni
vertice la parallela al lato opposto.Vogliamo dimostrare che le altezze di
questo triangolo passono per uno stesso punto,osserviamo che i quadrilateri
ABCP ed ACBQ sono parallelogrammi per
cui abbiamo AP=AQ e ciò dimostra che A è il punto medio del segmento PQ. Poi la
retta AA' del triangolo ABC è l'asse del segmento PQ. In tal modo si prova che
le rette BB' e CC' sono gli assi dei segmenti QO ed OP.Allora, essendo le rette
AA',BB' e CC' gli assi dei lati del triangolo OPQ, si intersecano nel punto H,
come si voleva dimostrare.
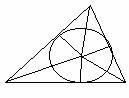
INCENTRO. Le bisettrici degli angoli interni di un
triangolo passano per uno stesso punto equidistante dai lati (detto incentro)
Sia dato il triangolo ABC vogliamo provare che le bisettrici dei suoi
angoli passono per un stesso punto P= punto comune delle bisettrici degli
angoli A e B siano PH ,PK ,PL le distanze del punto P dai lati del
triangolo.Poichè P è equidistante dagli angoli A e B, si ha PH=PL e PH=PK
dunque 131g65b si ottiene PL=PK. Quindi P è equidistante dai lati dell' angolo C.
Dunque le tre bisettrici del triangolo passono tutte per il punto P.
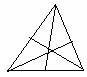
BARICENTRO. Le
mediane passano per uno stesso punto detto baricentro,che divide ciascuna
mediana in due parti , di cui quella contenente il vertice è il doppio
dell'altra.
Sia dato il triangolo ABC. Detto G il punto comune alle mediane AM e BM',
proviamo che AG=2 x GM e BG=2 x GM'. Il segmento MM' è parallelo ed è uguale
alla metà del lato AB e anche NN'.Il parallelogramma MM'NN' avendo come
diagonali le mediane dei lati otteniamo; AN'=N'G=GM e BN=NG=GM', ossia AG= 2GM
e BG= 2GM'
POLIGONI INSCRITTI E CIRCOSCRITTI
Un poligono si dice inscritto in una circonferenza quando i suoi
vertici stanno sulla circonferenza, questa a sua volta si dice circoscritta al
poligono
Un poligono si dice circoscritto ad una circonferenza quando i suoi lati
sono tangenti alla circonferenza, che a sua volta si dice inscritta nel
poligono.
QUADRILATERI INSCRITTIBILI IN UNA
CIRCONFERENZA.
T.
In un quadrilatero inscritto in una
circonferenza gli angoli opposti sono supplementari.
Proviamo che gli angoli opposti A^e C^ sono supplementari.Infatti l'angolo alla
circonferenza A^ è la metà del corrispondente angolo al centro BO^D; l'angolo
alla circonferenza C^ è uguale alla metà dell'angolo al centro BOD che insiste
sull'arco BAD. Poichè la somma dei due angoli al centro è un angolo giro,segue
che la somma A^+C^ è la metà di un angolo giro.
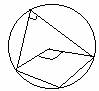
QUADRILATERI
CIRCOSCRITTIBILI AD UNA CIRCONFERENZA
T. Se un quadrilatero è circoscritto ad una circonferenza, la somma di due
lati opposti è congruente alla somma degli altri due.
Sia ABCD un quadrilatero circoscritto ad una circonferenza. Vogliamo dimostrare
che AB+CD=AD+BC. Allora T,T',P,P' siano i punti in cui la circonferenza tocca i
lati AB,BC,CD,DA.Perciò abbiamo che AT=AP' CP=CT' BT=BT' DP=DP'.Da cui
addizionando membro a membro abbiamo AB+CD=AD+BC
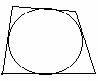
POLIGONI
REGOLARI
Un poligono si dice regolare quando ha i lati e gli angoli congruenti, cioè
quando è equilatero ed equiangolo.
Teorema: ad ogni poligono regolare si può circoscrivere e inscrivere una
circonferenza e le due circonferenze hanno lo stesso centro.
Teorema: se una circonferenza è divisa in un qualsivoglia numero di archi
congruenti, il poligono inscritto ottenuto congiungendo successivamente i punti
di suddivisione è regolare ed è regolare anche il poligono circoscritto i cui
lati sono tangenti alla circonferenza in quei punti.
T. Il lato dell'asegono regolare inscritto in una circonferenza è uguale
al raggio della circonferenza.
Sia ABCDEF un esagono regolare inscritto in una
circonferenza di centro O e raggio R.Vogliamo dimostrare che AB=R.Il triangolo
AOB, perchè OA=OB=R,l'angolo al vertice AO^B è di 60 gradi perchè è un sesto
dell'angolo giro,e puindi gli angoli alla basse sono 60 gradi ciascuno.Allora
il triangolo OAB è equiangolo e quindi equilatero, perciò essendo OA=OB=R ,è
anche AB=R
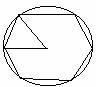
TRAPEZIO
T. Un trapezio è equidistante ad un triangolo avente la base uguale alla somma delle basi del trapezio ed uguale altezza.
Ip.=BE=CD Tesi= ABCD=AED.
(BE=DC per costruzione
DCM=BEM => ( CDM=MEB alterni interni delle parallele DC e AE tagliate da DE
( DCM=MBE alterni interni delle parallele DC e AE tagliate da BC
2 criterio=>ABCD=ABMD+DCM
AED=ABMD+BEM 5°postulato

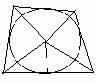
POLIGONO CIRCOSCRITTO AD UN CERCHIO
T. Un poligono circoscritto ad una circonfereza è equivalente ad un triangolo che ha la base uguale al perimetro del poligono e l'altezza uguale al raggio della circonferenza.
C. Un poligono regolare è equivalente ad un triangolo avente base ed altezza rispettivamente uguali al perimetro ed all'apotema del poligono.
TEOREMA DI PITAGORA
T. In ogni triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
Sia ABC il triangolo. Costruiamo sull'ipotenusa il quadrato BCDE, sul cateto AB il quadrato che indicheremo con Q1 e sul cateto AC il quadrato contrassegnato con Q2. Vogliamo dimostrare che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati Q1, Q2 costruiti sui cateti. Condotta per A la perpendicolare a BC, si viene a scomporre il quadrato BCDE nei due rettangoli BLME, LCDM che indicheremo rispettivamente con R1, R2. Per il primo teorema di Euclide abbiamo: R1=Q1; R2=Q2.
Da ciò segue per il terzo postulato sull'equivalenza che R1 + R2=Q1 + Q2.
Dunque, il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
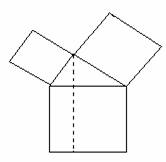
PRIMO TEOREMA DI EUCLIDE
T. In ogni triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo che ha per dimensioni l'ipotenusa e la proiezione del cateto stesso sull'ipotenusa.
Dato il triangolo ABC si costruiscano, come mostra la figura, il quadrato ABDE=Q ed il rettangolo BFGH=R, avente per dimensione la proiezione BF del cateto BA sull'ipotenusa ed il segmento BH uguale all'ipotenusa BC. Vogliamo dimostrare che Q = R. Le rette BH ed AF intersecano la retta DE rispettivamente nei punti I e K. Il quadrilatero IKAB = P è un parallelogramma perché i suoi lati opposti sono paralleli per costruzione.
I triangoli rettangoli ABC, DBI sono uguali in quanto hanno: AB=DB come lati del quadrato Q, ABC=DBI perché complementari dello stesso angolo IBA. Segue da ciò che sono uguali le loro ipotenuse BC,BI. D'altra parte è BC=BH per costruzione. Per cui si conclude che è BI=BH. Il rettangolo R ed il parallelogramma P, oltre ad avere uguale altezza BF (perché compresi fra le parallele HI, GK), hanno dunque uguali anche le basi BI, BH; per cui essi sono equivalenti. Analogamente sono equivalenti il parallelogramma P ed il quadrato Q che hanno la stessa base AB ed uguali altezze (perché entrambi compresi nella striscia di lati BA, DK). Pertanto, avendosi R=P e P=Q, si conclude che R=Q.
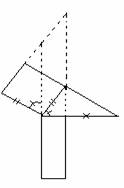
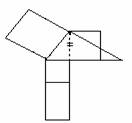
SECONDO TEOREMA DI EUCLIDE
T. In ogni triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull'ipotenusa.
Dato il triangolo ABC, si costruiscano sull'altezza AD relativa all'ipotenusa, sulla proiezione BD del cateto BA e sul cateto BA, rispettivamente i quadrati: ADGH=Q1; DBIK=Q2 ; Baml=Q3.
Si costruisca poi il rettangolo IFEK=R avente le dimensioni IF, IK rispettivamente uguali alle proiezioni DC, BD dei cateti sull'ipotenusa e si osservi che il rettangolo BFED=Q2 + R ha l'altezza BF uguale all'ipotenusa BC. Vogliamo dimostrare che Q1 = R. Per il primo teorema di Euclide e per il teorema di Pitagora apllicati rispettivamente ai triangoli rettangoli ABC, ADB, abbiamo:
Q3=Q2 + R; Q3=Q1 + Q2.
Ne segue, per la proprietà transitiva dell'equivalenza che Q1 + Q2 = Q2 + R. Sottraendo Q2 da ambo i membri otteniamo Q1=R.
GRANDEZZE OMOGENEE E LORO MISURA
CLASSI DI GRANDEZZE
Due grandezze si dicono omogenee se si possono confrontare e si possono sommare; per esempio due segmenti o due angoli sono grandezze omogenee, un segmento ed un'area non sono grandezze omogenee perché non ha senso confrontarle o sommarle.
Un insieme di enti geometrici costituisce una classe di grandezze omogenee o della stessa specie,ogni volta che per tali enti possono definirsi i concetti di uguaglianza e di disiguaglianza, nonchè l'operazione di addizzione.
Due grandezze non omogenee si dicono eterogenee.
Proprietà:
Ogni grandezza è uguale a se stessa (riflessiva)
Se una grandezza A è uguale ad una grandezza B, allora B è uguale ad A (simmetrica)
Due grandezze uguali ad una terza sono uguali tra loro (transitiva)
Se una grandezza è maggiore di un'altra e questa è maggiore di una terza allora la prima è maggiore della terza.(transitiva della disuguaglianza) Se A>B e se B>C allora A>C
Date due grandezze A e B, si verifica sempre uno ed uno solo dei seguenti casi: A=B, A<B, A>B
La somma di due o più grandezze non cambia se si cambia l'ordine di esse (commutativa)
La somma di due o più grandezze non cambia se a due o più di esse si sostituisce la loro somma(associativa)
Somme di grandezze uguali sono uguali
Differenze di grandezze uguali sono uguali.
MULTIPLI E SOTTOMULTIPLI DI UNA GRANDEZZA
Data una grandezza B ed un numero naturale m, la grandezza A somma di m grandezze tutte uguali a B si dice multipla di B secondo m. A= mB
*B è sottomultipla di A secondo il numero m. B= 1/m A
Postulato della divisibilità.Ogni grandezza è sempre divisibile in un numero qualunque di parti uguali.
Ammette che esiste sempre la sottomultipla B di A secondo m: B=1/m A ossia A= mB
Postulato di Eudosso-Archimede.Date due grandezze omogenee disuguali,esiste sempre una multipla della minore che supera la maggiore.
GRANDEZZE COMMENSURABILI ED INCOMMENSURABILI
Due grandezze omogenee si dicono commensurabili se ammettono una sottomultipla comune; si dicono incommensurabili se non ammettono una sottomultipla comune.
T. Il latoe la diagonale di un quadrato sono segmenti incommensurabili.
RAPPORTO DI DUE GRANDEZZE
*Il rapporto di due grandezze commensurabili è un numero razionale
T. Se il rapporto di due grandezze è un numero razionale, allora le due grandezze sono commensurabili
*Il rapporto di due grandezze incommensurabili è un numero irrazionale
NUMERI REALI=Due numeri reali sono uguali se hanno gli stessi valori approssimati per difetto e per eccesso.
POSTULATO DELLA CONTINUITA'=Due insiemi separati di grandezze di una stessa classe ammettono almeno un elemento di separazione.
T. Due insiemi continui di grandezze ammettono un solo elemento di separazione.
MISURA
DELLE GRANDEZZE= Dicesi misura di una grandezza A rispetto ad un'altra U omogenea con A, il
numero reale ![]() che espime il rapporto di A ad U. A/U=
che espime il rapporto di A ad U. A/U= ![]()
T. Il rapporto di due grandezze omogenee è uguale al quoziente delle loro misure rispetto ad una stessa unità.
PROPORZIONI TRA GRANDEZZE= Quattro grandezze A,B,C,D, si dicono in proporzione se il rapporto tra A e B è uguale al rapporto tra C e D. A:B=C:D
T. la condizione necessaria affinchè quattro grandezze siano in proporzione, è che siano in proporzione le loro misure.
Proprietà:
In ogni proporzione tra grandezze si può scambiare ogni antecedente col suo conseguente (prop. dell'invertire) B:A=A:D
In ogni proporzione tra grandezze tutte omogenee, si possono scambiare i medi oppure gli estremi (prop. del permutare) A:C=B:D e D:B=C:A
In ogni proporzione tra grandezze la somma dei promi due termini sta al primo come la somma degli altri due termini sta al terzo. (prop. del comporre) (A+B):A=(C+D):C e (A+B):B(C+D):D
In ogni proporzione tra grandezze,se ogni antecedente è maggiore del proprio conseguente,la differenza tra il primo ed il secodo termine sta al primo come la differenza tra il terzo ed il quarto termine sta al terzo. (A-B):A=(C-D):C e (A-B):B=(C-D):D
In ogni serie di rapporti uguali tra grandezze tutte omogenee,la somma degli antecedenti sta a quella dei conseguenti come un antecedente sta al proprio conseguente. (A+C+E):(B+D+F)=C:D
Se quattro grandezze sono in proporzione,secondoche la prima è uguale ,maggiore o minore della seconda,anche la terza è uguale ,maggiore o minore della quarta.
7) TEOREMA DELLA QUARTA PROPORZIONE.Date tre grandezze A,B,C con A e B omogenee tra loro,esiste ed è unica la grandezza D,omogenea con C, che è quarta proporzionale dopo A,B,C.
8)COROLLARIO.Se due proporzioni hanno tre termini ordinamente uguali,allora anche i rimanenti termini sono uguali.
AREA DEI POLIGONI
RETTANGOLO=è uguale al prodotto della misura della base per quella dell'altezza
I rettangoli R e R' hanno uguale altezze perciò stanno tra loro come le rispettive basi,abbiamo R:R'=B:U
In tal modo R' e Q hanno uguali basi perciò stanno tra loro come le rispettive altezze. R':Q=H:U
Allora le aree A di R e A' di R' per il teorema fondamentale delle proporzioni tra grandezze si ottiene
A:A'=b:1 ed A':1=h:1. da si ottiene A=b x h
QUADRATO=è uguale al quadrato della misura del lato.
Il quadrato è un rettangolo che ha la base uguale all'altezza. A= l"2
PARALLELOGRAMMO=è uguale al prodotto della misura della base per quella dell'altezza.
Infatti sapendo che il parallelogramo è equivalente ad un rettangolo abbiamo A= b x h
TRIANGOLO=è uguale al semiprodotto della misura della base per quella dell'altezza
Sapendo che il triangolo è equivalente ad un parallelogrammo che ha uguale altezza e base metà del triangolo abbiamo A= b x h diviso 2
TRIANGOLO RETTANGOLO=può ottenersi come semiprodotto delle misure dei cateti
Infatti in ogni triangolo l'altezza relativa ad un cateto è l'altro cateto. Si osservi altresì che
L'area di un triangolo rettangolo può anche ottenersi come prodotto delle misure dei due segmenti in cui l'ipotenesa è divisa dal punto di contatto con la circonferenza inscritta.
TRAPEZIO=è uguale al semiprodotto della somma delle misure delle basi per la misura dell'altezza.
A=(B+b) x h diviso 2. Si osservi che:
L'area di un trapezio rettangolo circoscrittibile ad una circonferenza può ottenersi come prodotto delle misure delle due basi. A= b x B
ROMBO=è uguale al semiprodotto delle misure delle diagonali . A= d x D diviso 2
POLIGONO CIRCOSCRITTO AD UNA CIRCONFERENZA=è uguale al prodotto della misura del semiperimetro del poligono per la lunghezza del raggio della circonferenza. A= p x r
AREA DEL POLIGONO REGOLARE=è uguale al prodotto della misura del semiperimetro per quella d'apotema A=p x a
TEOREMA DELLA BISETTRICE DELL'ANGOLO INTERNO.
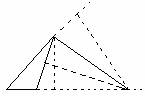
T. La bisettrice di un angolo interno di un triangolo divide il lato opposto in parti proporzionali agli altri due lati.
Vogliamo dimostrare la seguente proporzione AD:DC=AB:BC. Notiamo che l'area di un triangolo può calcolarsi assumendo come base uno qualunque dei lati. Allora indicando con A l'area del triangolo ABD e con A quello BCD, abbiamo 2S=AD x BH e 2A=DC x BH. Da cui avremo delle proporzioni che dividendo membro a membro si ottiene AD:DC=AB:BC
TEOREMA DELLA BISETTRICE DELL'ANGOLO ESTERNO.
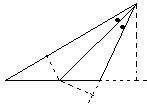
T. La bisettrice di un angolo interno di un triangolo incontra il prolungamento del lato opposto,qualora non sia ad esso parallela,in un punto le cui distanze dagli estremi di quel lato sono proporzionali agli altri due lati.
Vogliamo dimostrare che AE:CE=AB:BC. Allora la bisettrice BE risulta parallela ad AC,si ha 2 x S=AE x BH
ed 2 x A=CE x BH avremo due proporzioni a cui dividendo membro a membro ci daranno AE:CE=AB:BC
APPLICAZIONE DELL'ALGEBRA ALLA GEOMETRIA
TRIANGOLO RETTANGOLO=(teorema di Pitagora)Dato il triangolo ABC rettangolo in C e dette a,b,c le misure dei cateti e dell'ipotenusa,applicando il t. Pitagora avremo la seguente formula c"2=a"2+b"2 da cui si ricavano le altre formule.Le regoli sono:1)La misura dell'ipotenusa di un triangolo rettangolo è uguale alla radice quadrata della somma dei quadrati delle misure dei cateti.
2)La misura di un cateto è uguale alla radice quadrata della differenza dei quadrati delle misure dell'ipotenusa e dell'altro cateto.
TRIANGOLO RETTANGOLO=( 1° teorema di Euclide)dette a' e b' le misure delle proiezioni dei cateti sull'ipotenusa ,si ha le seguenti formule a"2=ca' e b"2=cb' da cui si ricavano le seguenti a=radice ca'
c=a"2/a' a'= a"2/c
La regola è: In ogni triangolo rettangolo ciascun cateto è medio proporzionale tra l'ipotenusa e la proiezione di quel cateto sull'ipotenusa; cioè la proporzione AH:CH=CH:BH
TRIANGOLO RETTANGOLO=( 2° teorema di Euclide)detta h la misura dell'altezza relativa all'ipotenusa ,abbiamo h"2=a'b' da cui si ottiene h=radice a'b' a'=h"2/b' b'=h"2/a'.
La regola è: In ogni triangolo rettangolo l'altezza relativa all'ipotenusa è media proporzionale tra le proiezioni dei cateti sull'ipotenusa.
QUADRATO=La misura della diagonale di un quadrato è uguale al prodotto della misura del lato per radice2
TRIANGOLO RETTANGOLO ISOSCELE=La misura dell'ipotenusa di un triangolo rettangolo con un angolo di 45° è uguale al prodotto della misura di un cateto per radice 2
TRIANGOLO EQUILATERO=(Altezza) La misura dell'altezza di un triangolo equilatero è uguale al prodotto della metà della misura del lato per radice 3
(Lato) La misura del lato di un triangolo equilatero è uguale al prodotto dei due terzi della misura dell'altezza per radice 3.
TRIANGOLO RETTANGOLO CON GLI ANGOLI ACUTI DI 30° E 60°
In un triangolo rettangolo con un angolo di 60°, il cateto minore è uguale alla metà dell'ipotenusa ed il cateto maggiore è uguale al prodotto del cateto minore per radice 3.Allora si ha AB=2 x HB
AH=HB x radice 3
TEOREMA DI TALETE
T. Le due classi di segmenti corrispondenti individuati da un fascio di rette parallele su due trasversali sono direttamente proporzionali.
Osservato che la corrispondenza che associa i segmenti AB, BC, CD,... della trasversale r rispettivamente ai segmenti A'B', B'C', C'D',... della trasversale r' è biunivoca, per provare l'enunciato applichiamo il primo criterio di proporzionalità. Pertanto dobbiamo dimostrare:
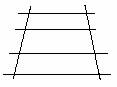
che a segmenti uguali di r corrispondono segmenti uguali di r' (Fig. 1);
che alla somma di due segmenti, presi su r, corrisponde, su r', il segmento somma dei due segmenti corrispondenti a quelli fissati su r (Fig. 2).
1) Sia AB=CD. Vogliamo provare che è pure A'B'=C'D'. Dette a,b,c,d le rette del fascio passanti rispettivamente per i punti A,B,C,D, conduciamo per A e per C le parallele alla r' che intersecano la prima la retta b in P e la seconda la retta d in Q. I triangoli ABP, CDQ sono uguali perchè hanno AB=CD per ipotesi, ABP=CDQ (angoli) perchè corrispondenti rispetto alle parallele b,d tagliate da r, BAP=DCQ (angoli) perchè corrispondenti rispetto alle parallele AP,CQ tagliate da r. Segue da ciò l'uguaglianza dei segmenti AP,CQ. D'altra parte si ha pure AP=A'B' e CQ=C'D' come lati opposti dei parallelogrammi APB'A' e CQD'C'; il che porta a concludere che si ha A'B'=C'D'.
2)Sia GH=CD + EF. Vogliamo dimostrare che G'H', corrispondente di GH, è la somma di C'D' ed E'F', rispettivamente corrispondenti di CD ed EF. Per le ipotesi fatte esiste un punto K del segmento GH che lo divide in due segmenti GK e KH rispettivamente uguali a CD ed EF. Sia k la retta del fascio passante per K e che interseca in K' la trasversale r'. Poichè abbiamo stabilito che a segmenti uguali di r corrispondono segmenti uguali di r', da GK=CD e KH=EF segue che G'K'=C'D' e K'H'=E'F'. Pertanto si conclude che G'H'=G'K' + K'H'=C'D' + E'F'
COROLLARIO DI TALETE
C. Una retta parallela ad un lato di un triangolo determina sugli altri due lati, o sui loro prolungamenti, segmenti proporzionali. (Fig.1)
Sia ABC un triangolo; conduciamo una parallela al lato BC, che interseca le rette AB, AC nei punti D, E. Per il vertice A tracciamo la parallela p a BC. Se applichiamo il teorema di Talete alle 3 parallele p, DE, BC e alle loro trasversali AB, AC abbiamo: AB:AC=AD:AE=DB:EC.

TEOREMA INVERSO DEL COROLLARIO DI TALETE
T. Una retta che determina su due lati di un triangolo, o sui loro prolungamenti, segmenti proporzionali, è parallela al terzo lato (inverso del precedente corollario). (Fig.2)
Dato un triangolo ABC, si consideri una retta che interseca le rette AB ed AC rispettivamente nei punti D ed E, tali che sia AB:DB=AC:EC. Vogliamo dimostrare che DE è parallela a BC. Ragioniamo per assurdo e supponiamo che DE non sia parallela a BC. In tal caso esisterebbe una retta DF, passante per D e parallela a BC, che incontrerebbe la retta AC in un punto F distinto da E. Per il precedente corollario si avrebbe: AB:DB=AC:FC. Confrontando tale proporzione con quella fornitaci dall'ipotesi del teorema si cade in assurdo.

|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025