|
|
| |
AREA DEI POLIGONI
RETTANGOLO=è uguale al prodotto della misura della base per quella dell'altezza
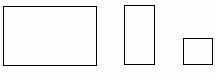
I rettangoli R e R' hanno uguale altezze perciò stanno tra loro come le rispettive basi,abbiamo R:R'=B:U
In tal modo R' e Q hanno u 828j99i guali basi perciò stanno tra loro come le rispettive altezze. R':Q=H:U
Allora le aree A di R e A' di R' per il teorema fondamentale delle proporzioni tra grandezze si ottiene
A:A'=b:1 ed A':1=h:1. da si ottiene A=b x h
QUADRATO=è uguale al quadrato della misura del lato.
Il quadrato è un rettangolo che ha la base uguale all'altezza. A= l"2
PARALLELOGRAMMO=è uguale al prodotto della misura della base per quella dell'altezza.
Infatti sapendo che il parallelogramo è equivalente ad un rettangolo abbiamo A= b x h
TRIANGOLO=è uguale al semiprodotto della misura della base per quella dell'altezza
Sapendo che il triangolo è equivalente ad un parallelogrammo che ha uguale altezza e base metà del triangolo abbiamo A= b x h diviso 2
TRIANGOLO RETTANGOLO=può ottenersi come semiprodotto delle misure dei cateti
Infatti in ogni triangolo l'altezza relativa ad un cateto è l'altro cateto. Si osservi altresì che
L'area di un triangolo rettangolo può anche ottenersi come prodotto delle misure dei due segmenti in cui l'ipotenesa è divisa dal punto di contatto con la circonferenza inscritta.
TRAPEZIO=è uguale al semiprodotto della somma delle misure delle basi per la misura dell'altezza.
A=(B+b) x h diviso 2. Si osservi che:
L'area di un trapezio rettangolo circoscrittibile ad una circonferenza può ottenersi come prodotto delle misure delle due basi. A= b x B
ROMBO=è uguale al semiprodotto delle misure delle diagonali . A= d x D diviso 2
POLIGONO CIRCOSCRITTO AD UNA CIRCONFERENZA=è uguale al prodotto della misura del semiperimetro del poligono per la lunghezza del raggio della circonferenza. A= p x r
AREA DEL POLIGONO REGOLARE=è uguale al prodotto della misura del semiperimetro per quella d'apotema A=p x a
TEOREMA DELLA BISETTRICE DELL'ANGOLO INTERNO.
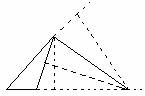
T. La bisettrice di un angolo interno di un triangolo divide il lato opposto in parti proporzionali agli altri due lati.
Vogliamo dimostrare la seguente proporzione AD:DC=AB:BC. Notiamo che l'area di un triangolo può calcolarsi assumendo come base uno qualunque dei lati. Allora indicando con A l'area del triangolo ABD e con A quello BCD, abbiamo 2S=AD x BH e 2A=DC x BH. Da cui avremo delle proporzioni che dividendo membro a membro si ottiene AD:DC=AB:BC
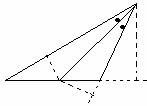
TEOREMA DELLA BISETTRICE DELL'ANGOLO ESTERNO.
T. La bisettrice di un angolo interno di un triangolo incontra il prolungamento del lato opposto,qualora non sia ad esso parallela,in un punto le cui distanze dagli estremi di quel lato sono proporzionali agli altri due lati.
Vogliamo dimostrare che AE:CE=AB:BC. Allora la bisettrice BE risulta parallela ad AC,si ha 2 x S=AE x BH
ed 2 x A=CE x BH avremo due proporzioni a cui dividendo membro a membro ci daranno AE:CE=AB:BC
APPLICAZIONE DELL'ALGEBRA ALLA GEOMETRIA
TRIANGOLO RETTANGOLO=(teorema di Pitagora)Dato il triangolo ABC rettangolo in C e dette a,b,c le misure dei cateti e dell'ipotenusa,applicando il t. Pitagora avremo la seguente formula c"2=a"2+b"2 da cui si ricavano le altre formule.Le regoli sono:1)La misura dell'ipotenusa di un triangolo rettangolo è uguale alla radice quadrata della somma dei quadrati delle misure dei cateti.
2)La misura di un cateto è uguale alla radice quadrata della differenza dei quadrati delle misure dell'ipotenusa e dell'altro cateto.
TRIANGOLO RETTANGOLO=( 1° teorema di Euclide)dette a' e b' le misure delle proiezioni dei cateti sull'ipotenusa ,si ha le seguenti formule a"2=ca' e b"2=cb' da cui si ricavano le seguenti a=radice ca'
c=a"2/a' a'= a"2/c
La regola è: In ogni triangolo rettangolo ciascun cateto è medio proporzionale tra l'ipotenusa e la proiezione di quel cateto sull'ipotenusa; cioè la proporzione AH:CH=CH:BH
TRIANGOLO RETTANGOLO=( 2° teorema di Euclide)detta h la misura dell'altezza relativa all'ipotenusa ,abbiamo h"2=a'b' da cui si ottiene h=radice a'b' a'=h"2/b' b'=h"2/a'.
La regola è: In ogni triangolo rettangolo l'altezza relativa all'ipotenusa è media proporzionale tra le proiezioni dei cateti sull'ipotenusa.
QUADRATO=La misura della diagonale di un quadrato è uguale al prodotto della misura del lato per radice2
TRIANGOLO RETTANGOLO ISOSCELE=La misura dell'ipotenusa di un triangolo rettangolo con un angolo di 45° è uguale al prodotto della misura di un cateto per radice 2
TRIANGOLO EQUILATERO=(Altezza) La misura dell'altezza di un triangolo equilatero è uguale al prodotto della metà della misura del lato per radice 3
(Lato) La misura del lato di un triangolo equilatero è uguale al prodotto dei due terzi della misura dell'altezza per radice 3.
TRIANGOLO RETTANGOLO CON GLI ANGOLI ACUTI DI 30° E 60°
In un triangolo rettangolo con un angolo di 60°, il cateto minore è uguale alla metà dell'ipotenusa ed il cateto maggiore è uguale al prodotto del cateto minore per radice 3.Allora si ha AB=2 x HB
AH=HB x radice 3
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024